Similar presentations:
Свойства степени с натуральным показателем
1. Разгадайте ребусы
СтепеньПовторение
Обобщение
2.
Урок повторения иобобщения по теме
«Свойства степени
с натуральным
показателем»
3. Цели:
1. Повторить и обобщить наши знания поданной теме.
2. Ликвидировать имеющиеся пробелы.
3. Подготовиться к изучению следующей темы.
4. «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.» М.В.Ломоносов
5. Повторим!
Сформулируйте определениестепени числа с натуральным
показателем.
6.
Степенью числа a с натуральнымпоказателем n, большим 1, называется
произведение n множителей, каждый из
которых равен а:
аⁿ = а·а·а·…·а
n
Степенью числа а с показателем 1
называется само число а:
а¹ = а
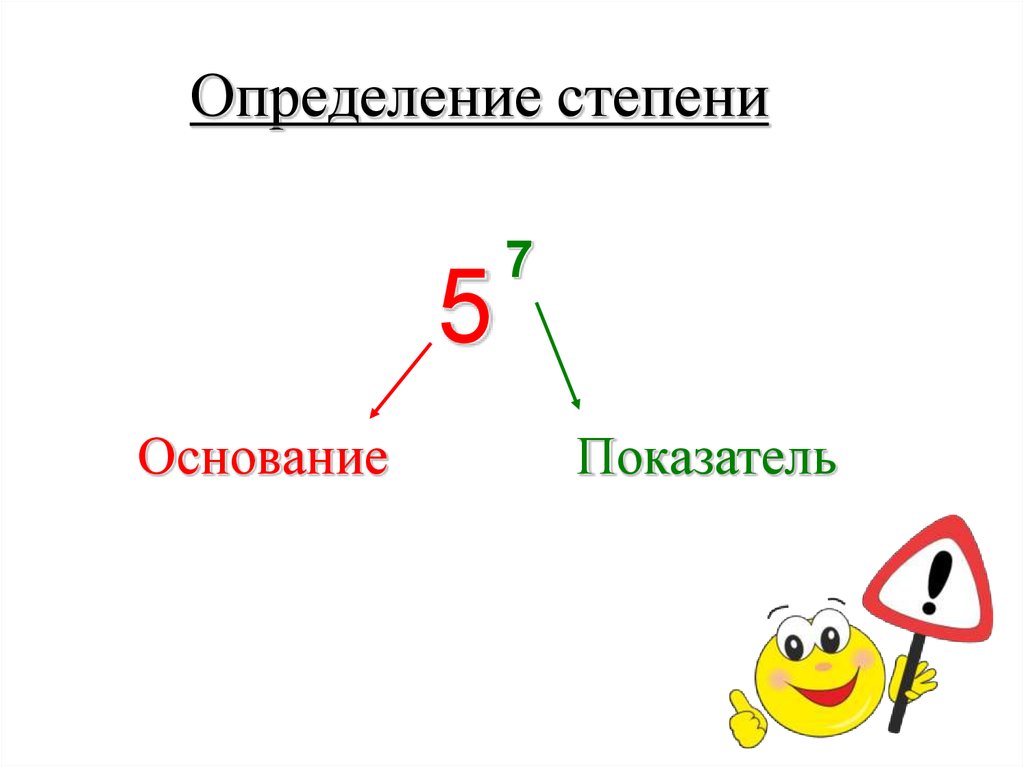
7.
Определение степени5
Основание
7
Показатель
8.
Умножение степеней с одинаковымиоснованиями
a a a
m
n
m n
При умножении степеней с
одинаковыми основаниями основание
оставляют прежним, а показатели
складывают.
9.
Деление степеней с одинаковымиоснованиями
a a a
m
n
При делении степеней с
одинаковыми основаниями
основание оставляют прежним, а
из показателя делимого
вычитают показатель делителя.
m n
10.
Возведение в степень степениa
m
n
a
mn
При возведении степени в степень
основание оставляют прежним, а
показатели перемножают.
11.
Возведение в степень дробиa
b
n
an
bn
При возведении в степень дроби возводят в эту
степень числитель и знаменатель дроби.
Возведение в степень произведения
ab
n
a b
n
n
При возведении в степень произведения возводят в эту
степень каждый множитель и результаты
перемножают.
12.
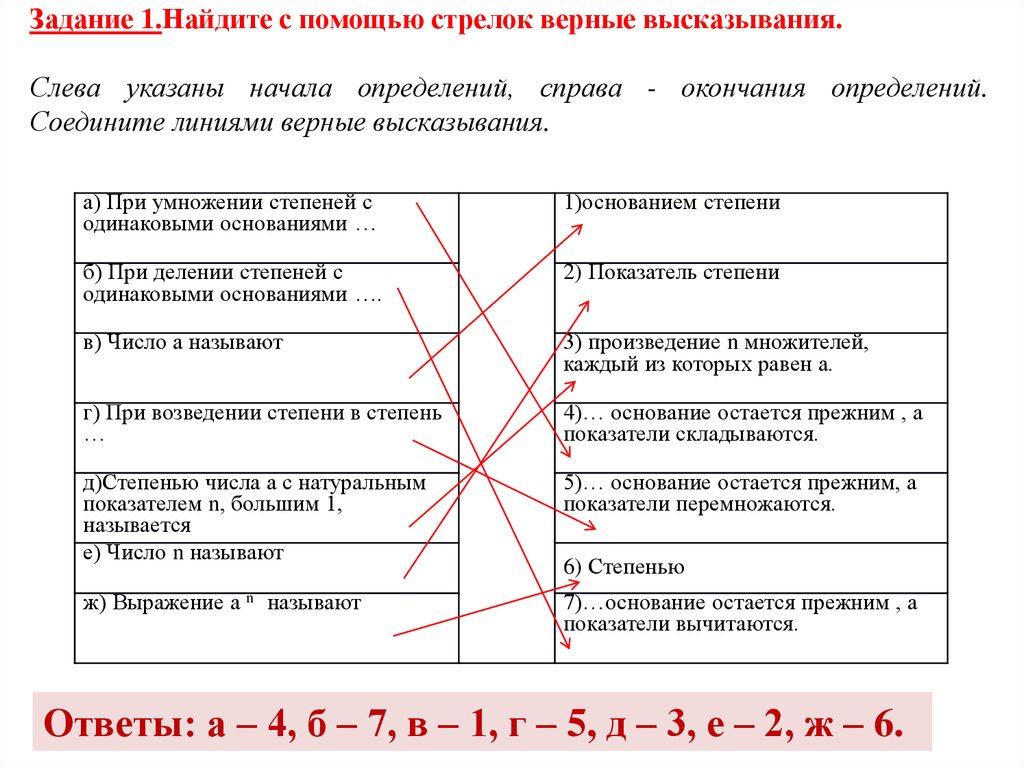
Задание 1.Найдите с помощью стрелок верные высказывания.Слева указаны начала определений, справа - окончания определений.
Соедините линиями верные высказывания.
а) При умножении степеней с
одинаковыми основаниями …
1)основанием степени
б) При делении степеней с
одинаковыми основаниями ….
2) Показатель степени
в) Число а называют
3) произведение n множителей,
каждый из которых равен а.
г) При возведении степени в степень
…
4)… основание остается прежним , а
показатели складываются.
д)Степенью числа а с натуральным
показателем n, большим 1,
называется
е) Число n называют
5)… основание остается прежним, а
показатели перемножаются.
ж) Выражение а n называют
7)…основание остается прежним , а
показатели вычитаются.
6) Степенью
Ответы: а – 4, б – 7, в – 1, г – 5, д – 3, е – 2, ж – 6.
13.
7 баллов – молодец!6 баллов – очень хорошо!
5 баллов – хорошо!
4 балла – не очень хорошо!
3 балла – плохо!
0-2 балла – очень плохо!
14.
Задание 2 (устно). Записать в виде степени4
3
у у уу
=
9
у
2
3
4
((х ) ) =
24
х
=
= 64
6
8
4
8
2
8
15.
Задание 3. Записать в виде степени с основанием с.Вариант 1.
Вариант 2.
1. С5 • С3
1. С7 : С5
2. С8 : С6
2. (С4)3 • С
3. (С4)3
3. С4 • С5 • С0
4. С5 • С3 : С6
4. С16 : С8
5. С14 • С8
5. (С3)5
Р
Ш
М
Ю
К
Н
А
Т
Е
Д
С8
С5
С1 С40 С13 С12 С9 С15 С2 С22
16.
17.
Особо следует отметить переработанную им математическуюсимволику, близкую к современной. Коэффициенты он
обозначал a, b, c…, а неизвестные — x, y, z.
Натуральный показатель степени принял современный вид.
18.
Задание 4. Определите, какие ответы правильные, а какиеложные.
• истинному ответу поставьте в соответствие 1, ложному – 0.
• получив упорядоченный набор из единиц и нулей, вы узнаете
имя еще одного известного математика.
а) x2 x3 = x5
б) s3 s5 s8 = s16
в) x7 : x4 = x28
г) (c+d)8 :(c+d) 7 = c+d
д) (x5 )6 = x 30
• Ада Августа Лавлейс
• Софи Жермен
• Исаак Ньютон
• Готфрид Вильгельм Лейбниц
11001
10101
11101
11011
19.
Задание 4. Определите, какие ответы правильные, а какиеложные.
• истинному ответу поставьте в соответствие 1, ложному – 0.
• получив упорядоченный набор из единиц и нулей, вы узнаете
имя еще одного известного математика.
а) x2 x3 = x5
б) s3 s5 s8 = s16
в) x7 : x4 = x28
г) (c+d)8 :(c+d) 7 = c+d
д) (x5 )6 = x 30
• Ада Августа Лавлейс
• Софи Жермен
• Исаак Ньютон
• Готфрид Вильгельм Лейбниц
11001
10101
11101
11011
20.
21.
В период работы над арифметической машиной Лейбниц занималсядвоичной системой счисления. В рукописи на латинском языке, подписанной
15 марта 1679 года, Лейбниц разъяснил, как выполнить вычисления в
двоичной системе счисления, в частности умножение, а позже разработал в
общих чертах проект вычислительной машины, работающей в двоичной
системе счисления.
Подробнее о трудах Лейбница, а также о том, кто из ученых стал развивать
его идеи, можно прочитать здесь:
https://ru.wikipedia.org/wiki/Лейбниц_Готфрид_Вильгельм
https://ru.wikipedia.org/wiki/Двоичная_система_счисления
22.
Задание 5. Решение задач.1. т · т4 · (т2)2 · т0
2. (23)7 : (25)3
3. (р2)4 : р5
4. (34)2 · (32)3 : 311






















 mathematics
mathematics








