Оптимизация с применением динамического программирования (ДП)

1.

1
ОПТИМИЗАЦИЯ
ХИМИКОТЕХНОЛОГИЧЕКИХ
ПРОЦЕССОВ
Модуль 4. Лекция.
Оптимизация с применением динамического
программирования (ДП)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

2.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
2
Для решения задач оптимизации многостадийных процессов
успешно применяется метод динамического
программирования - ДП, который позволяет снять ряд
трудностей, возникающих при решении многомерных задач.
Основным преимуществом этого метода является
возможность снизить размерность решаемой задачи.
Наиболее часто метод динамического программирования
используется при решении:
задач о распределении ресурсов по стадиям процесса
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

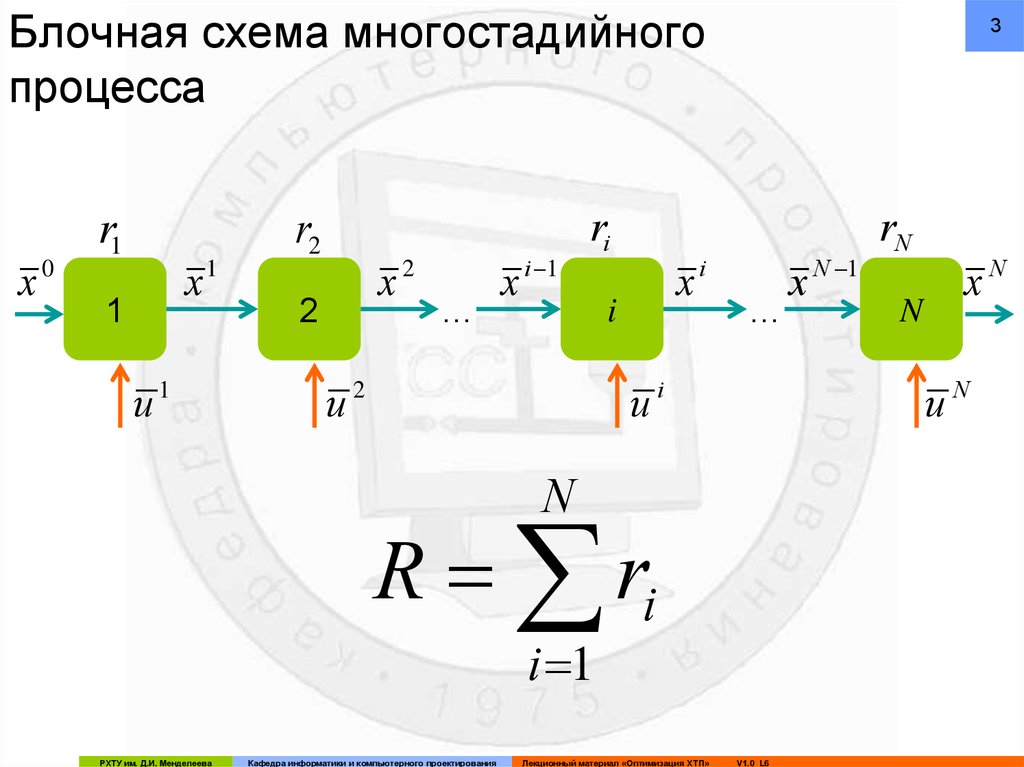
3. Блочная схема многостадийного процесса

x
r1
x
0
1
u
r2
x
1
1
2
u
2
…
x
i 1
ri
x
i
u
2
3
i
…
i
R ri
i 1
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x
N
u
N
РХТУ им. Д.И. Менделеева
x
N 1
rN
V1.0 L6
N
N

4.

4
Условные обозначения на схеме каскада аппаратов:
N
- число стадий процесса (аппаратов)
x i - вектор переменных состояния процесса на выходе
из i-того аппарата и на входе в i+1 аппарат
u i - вектор переменных управления i-том аппарате
ri - частный критерий оптимальности в i-том аппарате
N
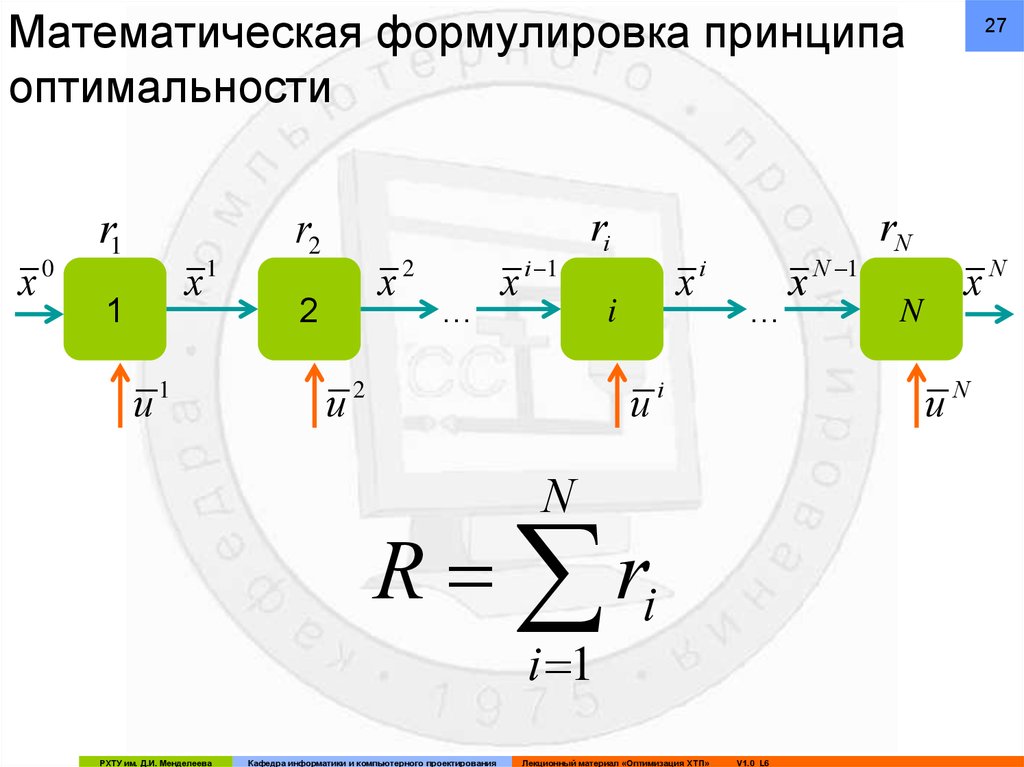
R ri - Критерий оптимальности всего процесса –
i 1
аддитивная функция
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

5.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
5
Критерий оптимальности на каждой стадии определяется её
состоянием:
ri ri ( x )
i
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

6.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
6
Уравнение математической модели для i –й стадии даёт
связь между вектором входных параметров, вектором
выходных параметров и вектором управлений:
x (x , u )
i
i 1
i
i
i 1,...N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

7.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
7
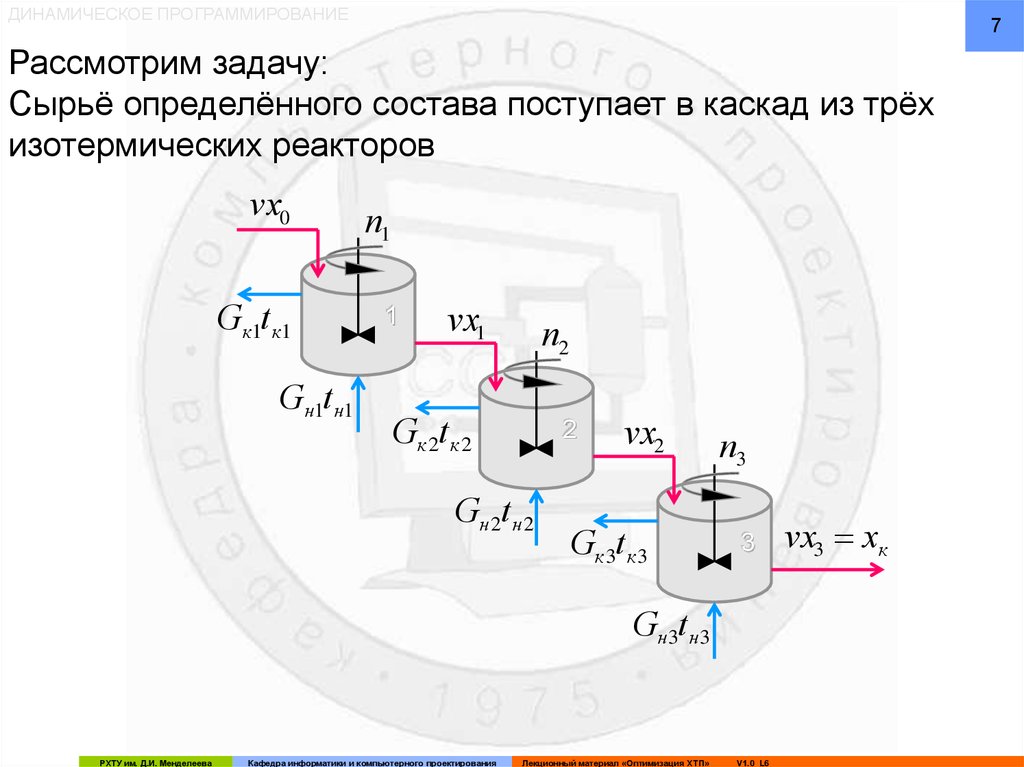
Рассмотрим задачу:
Сырьё определённого состава поступает в каскад из трёх
изотермических реакторов
vx0
Gк1tк1
Gн1t н1
n1
1
vx1
n2
Gк 2tк 2
2
Gн 2tн 2
vx2
Gк 3tк 3
n3
3
Gн3tн3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6
vx3 xк

8.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
8
По техническому регламенту для каждого реактора
допускается реализация трёх стационарных состояний,
определяемых набором параметров:
n – число оборотов мешалки
tн – температура хладагента
G – расход хладагента
Каждому стационарному состоянию соответствует некоторый
состав на выходе из аппарата:
xi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

9.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
9
Вектор искомых управляющих переменных на каждой стадии
имеет вид:
n – число оборотов мешалки
tн – температура хладагента
G – расход хладагента
n
u t Н
G
Тогда задача оптимизации формулируется следующим
образом:
i
max R (u )
u u
i
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
доп
Лекционный материал «Оптимизация ХТП»
V1.0 L6

10.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
10
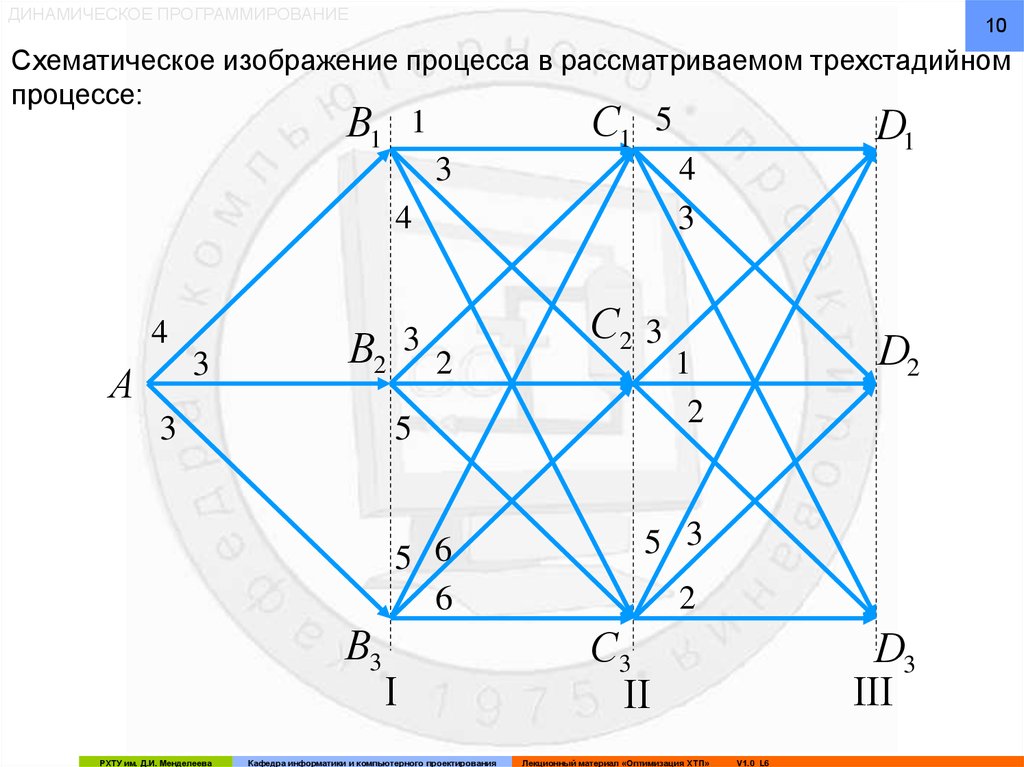
Схематическое изображение процесса в рассматриваемом трехстадийном
процессе:
B1
C1
1
4
3
3
4
4
3
A
B2
3
3
2
B3
РХТУ им. Д.И. Менделеева
C2
3
Ι
Кафедра информатики и компьютерного проектирования
D2
1
2
5
5 6
6
D1
5
5 3
2
C3
ΙΙ
Лекционный материал «Оптимизация ХТП»
D3
ΙΙΙ
V1.0 L6

11.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
11
Задача оптимизации ставится следующим образом:
найти такой набор управлений на каждом из реакторов,
чтобы критерий оптимальности всего процесса R достиг
максимального значения. В соответствии со схемой,
решение задачи оптимизации методом перебора всех
вариантов управлений, т.е. комбинаторным методом это
означает такой выбор одной или нескольких ломаных линий
из всей их совокупности, чтобы выполнилось следующее
равенство:
N
R ri max
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

12.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
12
Точка A изображает начальное состояние процесса, которое
характеризуется начальным составом сырья, его
температурой и т.д. В результате определённого набора
управлений на первом реакторе (n1, tн1, G1) на выходе из него
получается продукт с составом:
x
1
j
j 1, 2, ..., k
k – соответствует числу состояний (k =3), реализуемых в
каждом случае.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

13.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
13
Далее переработка сырья во втором реакторе
осуществляется таким образом, что на выходе из него
получается следующий состав продуктов:
x ,x ,x
2
1
2
2
2
3
Эти состояния изображаются точками C1, C2 и C3. Линии,
соединяющие точки Bi и Cj, соответствуют тем наборам
управлений на втором реакторе, которые используются при
переводе системы из состояния Bi в состояние Cj.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

14.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
14
Аналогично для третьего реактора точки D1, D2 и D3
соответствуют трём возможным стационарным
состояниям на третьем реакторе, т.е. составам:
x ,x ,x
3
1
3
2
3
3
Линии, соединяющие точки Ci и Dj, соответствуют тем
наборам управлений на третьем реакторе, которые
используются при переводе системы из состояния Ci в
состояние Dj.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

15.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
15
Далее предположим, что реализация любого управления на
любом реакторе связана с некоторым значением критерия
оптимальности в этом реакторе. На схеме цифрами
проставлены условные значения критерия оптимальности на
каждой стадии в зависимости от применяемого набора
управлений. При этом будем считать, что критерий
оптимальности всего процесса может быть выражен в виде:
N
R ri
i 1
ri – значение критерия оптимальности в i-ом реакторе
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

16.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
16
Проще всего эта задача может быть решена обычным
перебором (1-ый способ решения), т.е. сравнением между
собой всех возможных вариантов проведения процесса.
Необходимо определить значение R для всех ломаных (здесь
27) схемы процесса:
AB1C1 D1 4 1 5 10
AB1C1 D2 4 1 4 9
AB1C1 D3 4 1 3 8
AB1C 2 D1 4 3 3 10
AB1C 2 D2 4 3 1 8
AB1C 2 D3 4 3 2 9
РХТУ им. Д.И. Менделеева
и т.д. до 27 строк
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

17.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
17
Из всех полученных значений R выбирается максимальный и,
следовательно, выбирается реализующий его набор
управлений.
Однако этот путь решения имеет существенный недостаток требуется производить анализ всех возможных вариантов, число
которых быстро возрастает с ростом числа стадий и числа допустимых состояний:
3 27
3
Для 5 стадий и 3 допустимых состояний число вариантов:
3 243
5
Для 10 стадий и 3 допустимых состояний число вариантов:
3 59049
10
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

18.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
18
Изложенный метод решения задачи требует реализации
большого количества необходимых вычислений.
Формула для количества возможных вариантов
вычислений при использовании метода перебора (1-ый
способ решения) имеет вид:
n k
N
k – число возможных состояний на стадии
N – число стадий
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

19.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
19
В соответствии с принципом оптимальности, которым
необходимо руководствоваться при решении таких задач, и
который лежит в основе динамического программирования
(2-ой способ решения):
для любого промежуточного состояния процесса
последующие управления должны быть оптимальными.
В соответствии с этим принципом решение задачи методом ДП включает
2 этапа:
1- этап: начинается с выбора оптимального управления на последней стадии,
затем на предпоследней и т.д., двигаясь от конца процесса к его началу. Однако
значения этих управлений зависят от входных параметров на каждую стадию,
включая первую стадию. Входные параметры на первую стадию либо известны,
либо определяются по результатам расчетов первой стадии.
2-этап: по известным значениям входных параметров, начиная с первой стадии
определяются конкретные управляющие параметры последовательно на всех
стадиях процесса до последней стадии, что и является решением задачи.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

20.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
20
Если же задача решается изложенным методом
динамического программирования (2-ой способ решения),
необходимое количество вычислений (n’ )составляет:
n' k ( N 1) k
2
При k = 3 и N = 3 n’ = 21, в то время как в 1-ом способе - n = 27
При k = 3 и N = 10 n’ = 93, в то время, как в 1-м - n = 59049.
При k = 3 и N = 5 n’ = 39, в то время, как в 1-м - n = 243.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

21.

Динамическое программирование
21
Большинство процессов химической технологии относится к
классу дискретно распределённых во времени и пространстве
процессов.
Пусть имеется каскад химических реакторов идеального
перемешивания, в котором проводится необратимая реакция
первого или второго порядка:
A P
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

22.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
22
Допустим, что задана конечная концентрация реагента A:
x AN xN
Число реакторов в каскаде N. Требуется выбрать объёмы
реакторов так, чтобы суммарный объём всех реакторов
был минимальным.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

23.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
23
Критерий оптимальности
N
R Vi
i 1
является функцией многих переменных, и решение задачи
методом неопределённых множителей Лагранжа становится
затруднительным.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

24. Формулировка принципа оптимальности Белмана

Оптимальная стратегия обладает таким
свойством, что каково бы ни было начальное
состояние и начальное решение, последующие
решения должны приниматься, исходя из
оптимальной стратегии относительно
состояния, получаемого в результате первого
решения
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

25. Общая схема решения задач методом динамического программирования

25
При подходе к решению задач оптимизации методом
динамического программирования необходимо обращать
внимание на следующее:
a) оптимизируемый процесс должен быть дискретнораспределённым во времени или пространстве
(многостадийный процесс);
b) отдельные стадии процесса должны обладать
относительной независимостью, т.е. вектор выходных
параметров любой стадии должен зависеть только от
вектора входных параметров на эту стадию и управлений
на ней;
c) критерий оптимальности всего процесса должен быть
сформулирован как аддитивная функция критериев
оптимальности каждой стадии;
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

26.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
26
При выполнении перечисленных условий необходимо
правильно формулировать задачу оптимизации. При
формулировке должны быть выявлены:
параметры, характеризующие состояние каждой стадии;
управляющие параметры на каждой стадии;
ограничения, которые накладываются на параметры
состояния процесса и управляющие параметры.
Необходимо составить:
1. математическое описание для каждой стадии;
2. критерий оптимальности.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

27. Математическая формулировка принципа оптимальности

x
r1
x
0
1
u
r2
x
1
1
2
u
2
…
x
i 1
ri
x
i
u
2
i
…
i
R ri
i 1
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
rN
x
N
u
N
РХТУ им. Д.И. Менделеева
x
N 1
27
V1.0 L6
N
N

28.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
28
Критерий оптимальности на каждой стадии определяется её
состоянием:
ri ri ( x )
i
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

29.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
29
Уравнение математической модели для i –й стадии даёт
связь между вектором входных параметров, вектором
выходных параметров и вектором управлений:
x (x , u )
i
i 1
i
i
i 1,...N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

30.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
30
Первый этап решения
Решение задачи начинается с последней стадии, где
необходимо выбрать оптимальное управление – так, чтобы
критерий оптимальности rN был экстремальным (например,
максимальным):
f1 min
r
(
x
)
N
N
N
u U
x (x
N
РХТУ им. Д.И. Менделеева
N
N 1
Кафедра информатики и компьютерного проектирования
N
,u )
Лекционный материал «Оптимизация ХТП»
V1.0 L6

31.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
31
Используя уравнение математической модели для данной
стадии, получим:
f1 ( x
N 1
) min
r
[
(
x
N
N
N
N 1
u U
, u )]
N
откуда определяется оптимальное управление uopt
которое зависит от выходных переменных предыдущей
стадии x N 1
N
opt
u
РХТУ им. Д.И. Менделеева
u (x
N
Кафедра информатики и компьютерного проектирования
N 1
)
Лекционный материал «Оптимизация ХТП»
V1.0 L6
N

32.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
32
Переходя к стадии N – 1, получим условие выбора
оптимального уравнения:
f 2 min
{
r
(
x
N
1
N 1
N 1
U
u
) f1 ( x
N 1
)}
где математическая модель предыдущей стадии имеет вид:
x
N -1
N 1
(x
N 2
,u
N 1
)
с зависимостями для управляющих переменных следующего
вида:
u
N 1
opt
РХТУ им. Д.И. Менделеева
u
N 1
Кафедра информатики и компьютерного проектирования
(x
N 2
)
Лекционный материал «Оптимизация ХТП»
V1.0 L6

33.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
33
Поскольку f1 уже выбрано, определение f2 даёт возможность
выбора оптимального управления на стадии N – 1. Подставляя
уравнение математической модели для данной стадии,
получим:
f2 (x
N 2
) min
{
r
[
N
1
N 1
u
f1[
N 1
U
N 1
(x
N 2
,u
(x
N 1
N 2
)]}
откуда определяется оптимальное управление
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
,u
Лекционный материал «Оптимизация ХТП»
V1.0 L6
N 1
uopt
N 1
)]

34.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
34
Проводя аналогичный анализ, для стадии i можно записать:
i 1
f N (i 1) ( x ) min
[
r
(
x
)
f
(
x
)]
i
N
i
i
i
u U
i
x (x , u )
i
u
РХТУ им. Д.И. Менделеева
i
opt
i 1
i
i
i 1
u (x )
i
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

35.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
35
С учётом φi получим математическую формулировку принципа
оптимальности, являющуюся рекуррентной формулой,
позволяющей выполнять решение задачи оптимизации
последовательно:
f N (i 1) ( x ) min
{
r
[
(
x
,
u
)]
i
i
i
i 1
i 1
u U
f N i [ i ( x , u )]}
i 1
i
где fN-(i-1) – значение суммы критериев оптимальности
последних N - i стадий.
i
uopt
откуда определяется оптимальное управление
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6
i

36.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
36
Для первой стадии имеем:
f N ( x ) min
{r1[ ( x , u )] f N 1[ ( x , u )]}
1
0
1
0
1
1
0
1
u U
откуда определяется оптимальное управление (А) или наряду
с оптимальным управлением и оптимальные входные
переменные (В) :
1
А)
u
opt
или 1
В) uopt ,
x 0 - более сложная задача (большей размерности)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

37.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
37
На этом завершается 1-этап решения задачи ДП.
Второй этап решения
1
u
Для реализация 2-этапа на основе знания opt и
по
соотношениям, приведенным ниже, последовательно
i
i
определяются x (i=1,…N) и uopt (i=2,…N):
u
1
opt
u (x )
1
opt
0
x (x , u )
1
РХТУ им. Д.И. Менделеева
i
Кафедра информатики и компьютерного проектирования
0
1
opt
Лекционный материал «Оптимизация ХТП»
V1.0 L6

38. Произвольная стадия каскада

38
Произвольная стадия каскада
i
opt
u
i 1
u (x )
i
opt
x (x , u )
i
i
i 1
i
opt
i 1,...N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

39.

39
Пример 1.
Пусть имеется каскад химических реакторов идеального
перемешивания, в котором проводится необратимая реакция
первого порядка:
A P
Задана конечная концентрация A:
xN
Число реакторов в каскаде N.
Задача оптимизации: выбрать объёмы реакторов так,
чтобы суммарный объём всех реакторов был
минимальным.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

40.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
40
Нетрудно видеть, что в поставленной задаче оптимизации
выполнены условия a, b и с: оптимизируемый процесс
является дискретно-распределённым в пространстве;
отдельные стадии процесса обладают относительной
независимостью (выход каждого реактора зависит только от
входящих переменных и управлений на нём) и критерий
оптимальности всего процесса является аддитивной
функцией частных критериев (критерий оптимальности объём каскада реакторов, частные критерии - объёмы
каждого аппарата).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

41.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
41
Запишем сведения о процессе, необходимые для решения
задачи оптимизации:
1. Параметрами, характеризующими состояние каждой стадии
являются концентрации продукта реакции или исходного
реагента - xi.
2. Управляющие параметры - объёмы каждого реактора или,
что то же самое, время пребывания смеси в каждом реакторе
Ui (при постоянной нагрузке).
3. На параметры состояния процесса на каждой стадии
наложены ограничения:
x0 xi xк
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

42.

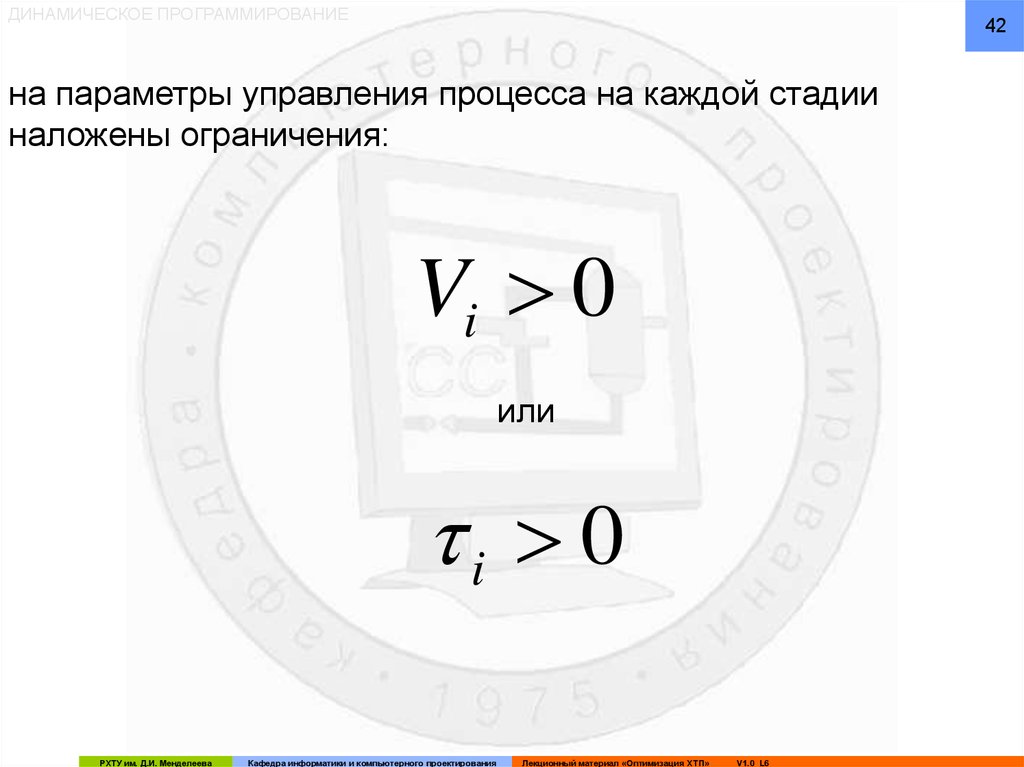
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
42
на параметры управления процесса на каждой стадии
наложены ограничения:
Vi 0
или
i 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

43.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
43
Составляем математическое описание каждой i-ой стадии
(уравнение материального баланса):
v( xi 1 xi ) Vi kxi 0
или
xi 1 xi k i xi 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

44.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
44
Откуда имеем:
xi 1
xi
1 k i
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

45.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
45
Составляем критерий оптимальности (Слайд 67) :
N
R V Vi
i 1
или
N
R i
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

46.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
46
Пример 1.
ПЕРВЫЙ ЭТАП РЕШЕНИЯ
решения выглядит следующим образом:
1 x N 1
f1 min
1
k
x
xN
N
где
1 xN 1
rN τ N
1
k xN
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

47.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
47
Концентрация реагента A на выходе из реактора N
однозначно определяет время пребывания в нём, поэтому
именно её можно взять в качестве управляющего
параметра.
Тогда задача оптимизации на последней стадии состоит в
выборе такой концентрации на выходе из N –го аппарата, при
которой время пребывания в N –ом аппарате было бы
минимальным.
Однако в рассматриваемой задаче конечная концентрация xN
задана, поэтому задача какого-либо выбора исключается и
остаётся только рассчитать время пребывания при заданном
значении xN:
1 x N 1
f1 ( x N 1 )
1
k xN
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

48.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
48
В соответствии с общей схемой переходим к предпоследнему
реактору:
1 x N 2 xN 1
f 2 min
1
1
x N 1
k
x
x
N
1
N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

49.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
49
Если вид выражения критерия не сложен, а названное
управление - это единственный управляющий параметр, то
для определения экстремума r*N на стадии можно
пользоваться теоремами математического анализа.
Если же выражение критерия сложно, а управление есть
совокупность нескольких управляющих воздействий, то
решение с использованием классического
дифференциального анализа или невозможно, или
представляет значительные трудности. Поэтому следует
применять методы нелинейного программирования.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

50.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
50
В предпоследнем реакторе необходимо выбрать такое
значение x N-1, чтобы выражение в скобках имело минимум при
любых значениях xN-2. Это значение xN-1 можно найти,
воспользовавшись необходимым условием существования
экстремума функции одной переменной:
x
x
d 1 N 2 N 1
1
1
dx N 1 k x N 1 x N
1 x N 2 1
2
0
k x N 1 x N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

51.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
51
Из последнего выражения следует:
x N 1( opt) ( xN xN 2 )
1/ 2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

52.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
52
Поскольку функция f2 дифференцируемая, легко проверить
достаточное условие существования экстремума:
d 1 xN 2 xN 1
1
1
2
dxN 1 k xN 1 x N
1 2 x N 2
3 0
k xN 1
2
во всём диапазоне изменения xN-1, следовательно
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

53.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
в точке
53
x N 1
Следовательно:
x N 1( opt) ( x N xN 2 )
1/ 2
функция f2 принимает минимальное значение.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

54.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
54
Чтобы получить минимальное значение времени пребывания
в двух последних реакторах, запишем рекуррентное
соотношение:
2 x N 2
f 2 ( xN 2 )
1
k xN
1
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

55.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
55
Повторим рассмотренную процедуру для третьего от конца
реактора. Запишем для него рекуррентное соотношение:
1
2
x
x
1
2
N 3
N 2
f 3 min
1
1
x N 2
k
x
k
x
N 2
N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

56.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
56
Найдём минимум, воспользовавшись необходимым условием
существования экстремума функции одной переменной:
1
2
d{выражение} 1 x N 3 2 1
1
0
2
*
x k 2 x N * x N 2
dx N 2
k
N 2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

57.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
57
Откуда получаем:
xN 2( opt) ( xN x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
2
N 3
Лекционный материал «Оптимизация ХТП»
V1.0 L6
)
1
3

58.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
58
Проверим достаточное условие:
d
dx N 2
1
2
1
1 x N 3 1
2
k
x
k
x
*
x
N N 2
N 2
1 2 x N 3 1
1
3
1/ 2 3 / 2
k xN 2 2 xN xN 2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

59.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
59
Подставив в последнее выражение полученное значение
оптимальной концентрации, имеем:
2 x N 3
1
1
1
2
1/ 3 3
1/ 2
2
1/ 3 3 / 2
k [( x N 3 x N ) ]
2 x N [( x N 3 x N ) ]
1 2
1
1
k x N 3 x N 2 x N 3 x N
0
т.е. при оптимальном значении концентрации действительно
достигается минимум.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

60.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
60
Подставив значение оптимальной концентрации в
рекуррентное соотношение, получим:
1
x N 3
1
2
1/ 3
k ( x N 3 x N )
f 3 ( x N 3 )
1/ 2
2
1
/
2
(
x
x
)
2 N 3 N
1
1/ 2
k
x
N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

61.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
61
или после преобразований:
3 x N 3
1
f 3 ( x N 3 )
k xN
1
3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

62.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
62
Решение задачи выполняется таким же образом
последовательно для всех реакторов до первого
включительно.
Для произвольного реактора i, считая от конца процесса,
получим аналогичные выражения оптимальной концентрации:
x N (i 1)( opt) ( xN x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
i 1
N i
V1.0 L6
)
1
i

63.

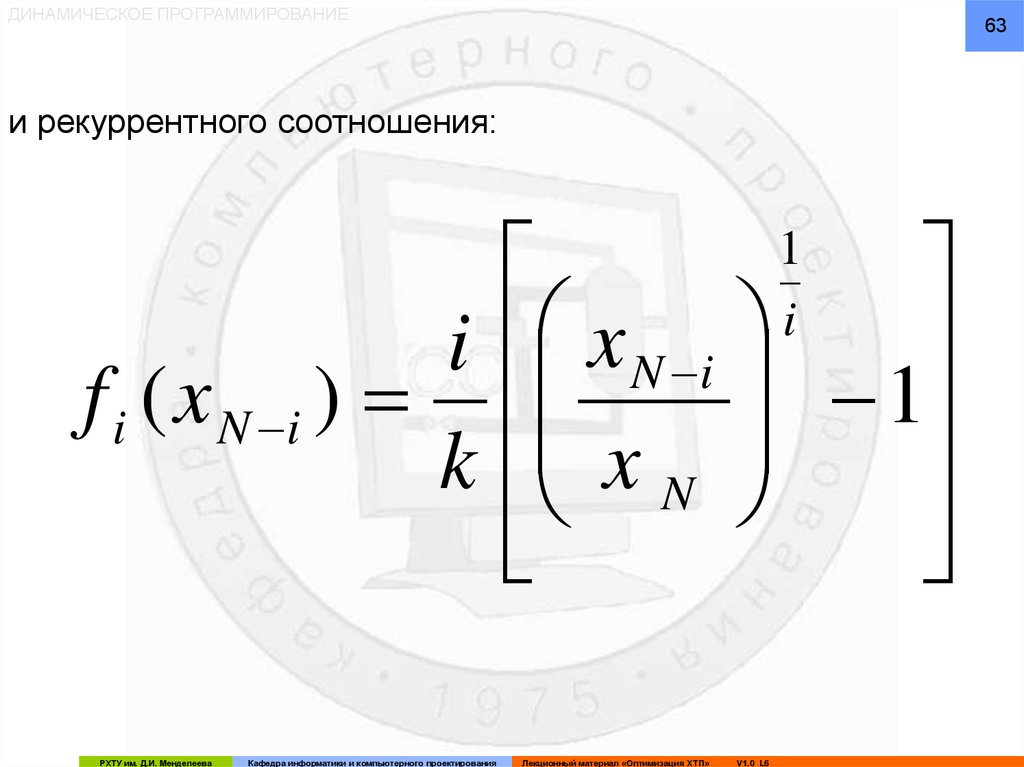
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
63
и рекуррентного соотношения:
i x N i
f i ( x N i )
k x N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1
i
1

64.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
64
Для первого реактора:
1
N 1 N
0
x 1( opt) ( xN x
)
N x 0
f N (x 0 )
k xN
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1
N
1

65.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
65
Поскольку в условии задачи x 0 и xN заданы, k и N неизвестны,
из последнего выражения рассчитывается минимальное
значение критерия оптимальности:
N
R i f N ( x0 )
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

66.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
66
и для первого реактора:
x 1( opt) ( xN x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
1
N 1 N
0
Лекционный материал «Оптимизация ХТП»
)
V1.0 L6

67.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
67
ВТОРОЙ ЭТАП РЕШЕНИЯ
На втором этапе решения из полученных соотношений
определяются:
x 1( opt)
1
( o p t)
РХТУ им. Д.И. Менделеева
1 x 0 x 1( o p t)
k x 1( o p t)
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

68.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
68
Для второго реактора имеем:
x 2( opt) ( xN x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
N 2
1( opt)
Лекционный материал «Оптимизация ХТП»
)
V1.0 L6
1
N 1

69.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
69
Далее определяется:
2
( o p t)
x
x
1 1( o p t)
2 ( o p t)
k
x2( o p t)
и т.д. до тех пор, пока не будут получены значения всех
оптимальных управлений.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

70.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
70
Далее определяется:
N
( opt)
x
x
1 N 1( opt)
N ( зад)
k
x N ( зад)
и т.д. до тех пор, пока не будут получены значения всех
оптимальных управлений.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

71.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
71
Пример 2
В каскаде реакторов идеального перемешивания проводится
простая реакция 2-го порядка : A → P. Каждый из аппаратов
каскада работает в изотермических условиях, причём
температура реакционной массы во всех аппаратах
одинакова.
Требуется определить среднее время пребывания
реакционной массы в каждом из аппаратов с тем, чтобы
общее время пребывания реакционной массы в системе было
минимальным.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

72.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
72
Исходные данные:
Число аппаратов N = 3
Начальная концентрация компонента A x0 = 1 моль/литр
Конечная концентрация компонента A на выходе из каскада x3
= 0,2 моль/литр
Константа скорости реакции:
литр
k 1
моль час
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

73.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
73
Решение
Критерий оптимальности процесса по условию задачи есть:
N
R τ τi
i 1
τi - среднее время пребывания в i – ом аппарате.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

74.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
74
Из уравнения материального баланса для i – го реактора
имеем:
xi 1 xi
i
2
k xi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

75.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
75
Первый этап решения
Записываем рекуррентное соотношение:
x 2 x3
f1 ( x2 ) min
x3 x k x 2
3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

76.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
76
Поскольку x3 задано,
x 2 x3
f1 ( x2 )
2
k x3
25 x 2 5
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

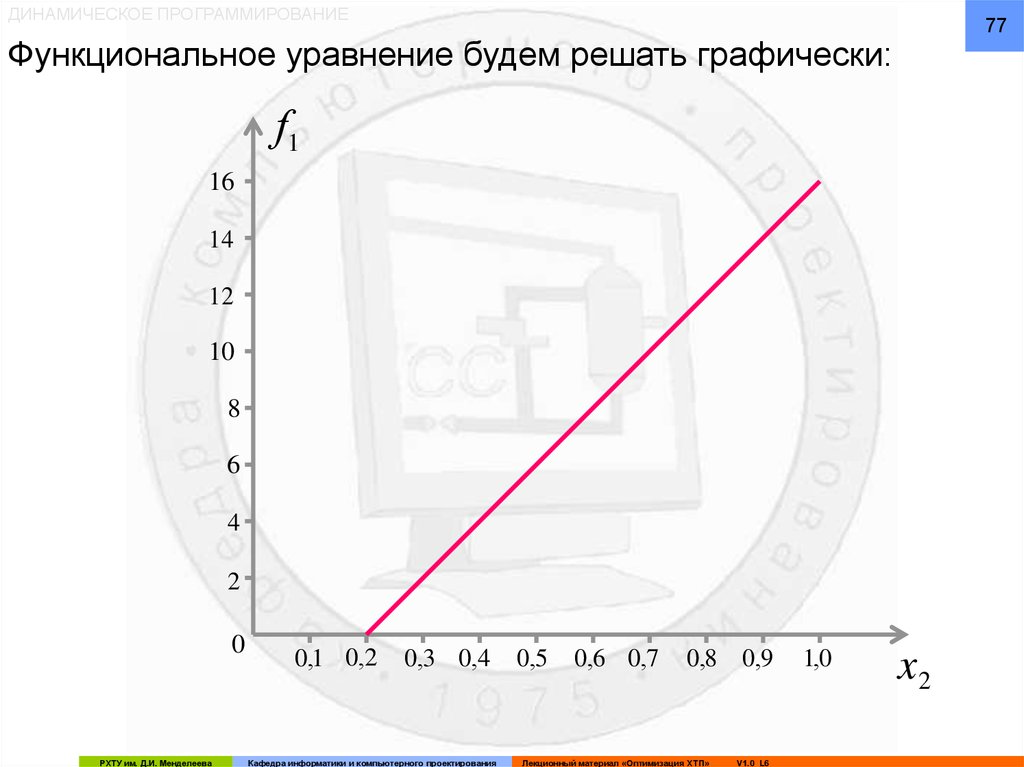
77.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
77
Функциональное уравнение будем решать графически:
f1
16
14
12
10
8
6
4
2
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x2

78.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
78
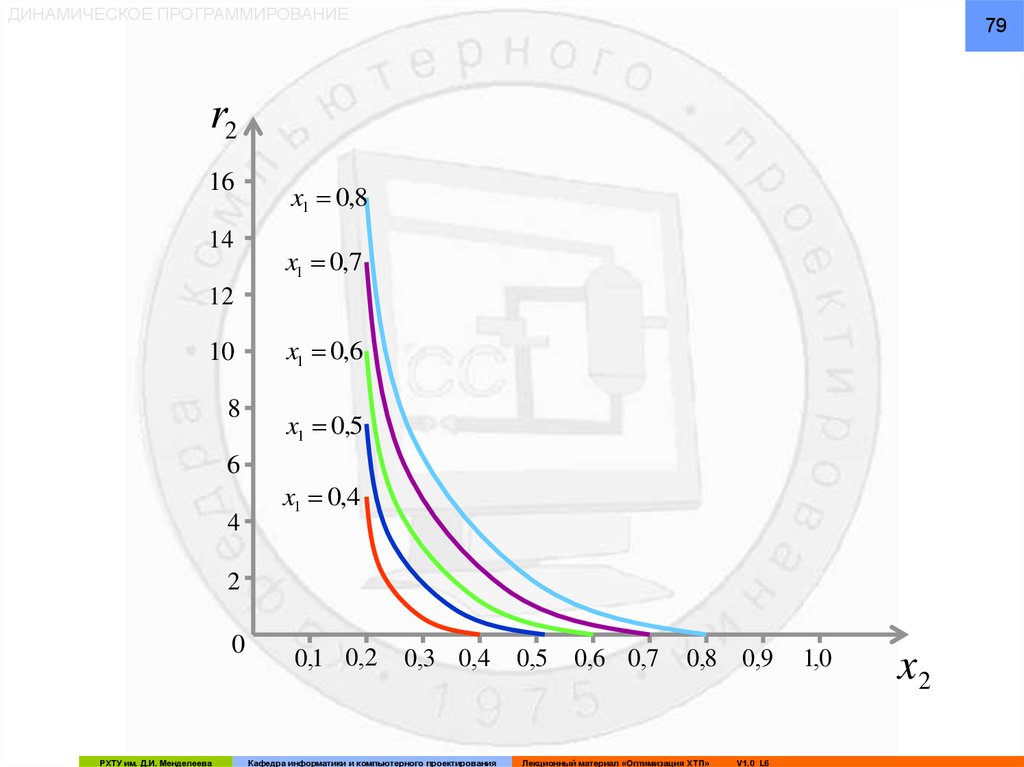
Записываем рекуррентное соотношение для f2:
x1 x2
f 2 ( x1 ) min
25
x
5
2
2
x2 x
k x2
r2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
f1
V1.0 L6

79.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
79
r2
16
14
x1 0,8
x1 0,7
12
10
x1 0,6
8
x1 0,5
6
4
x1 0,4
2
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x2

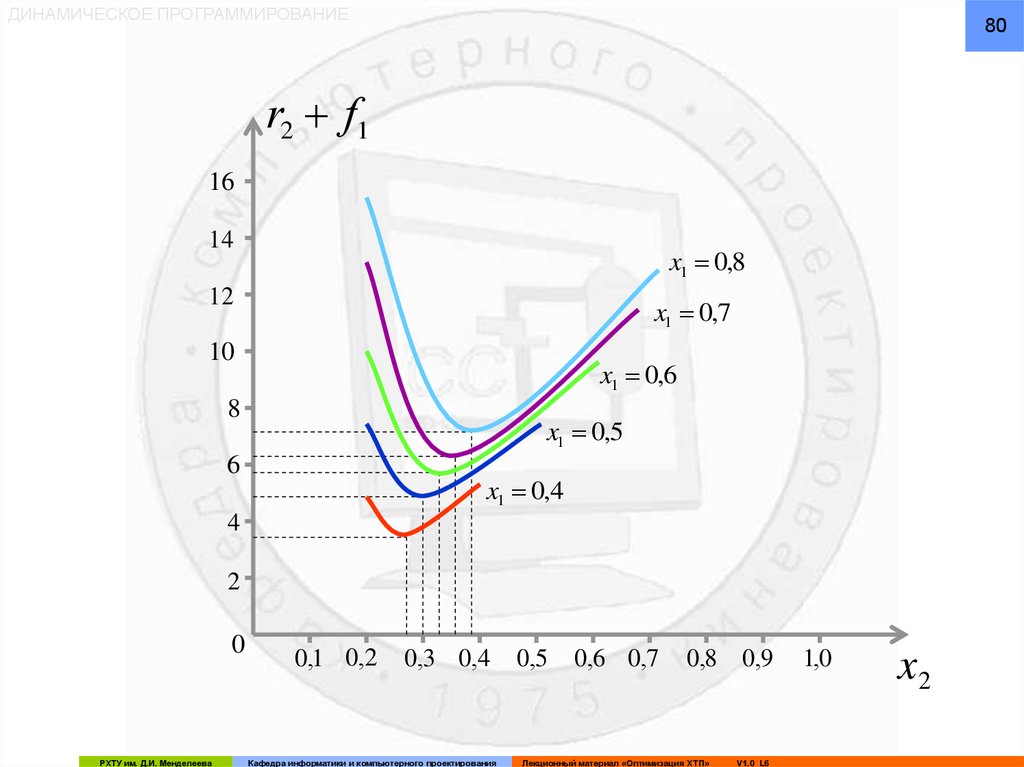
80.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
80
r2 f1
16
14
x1 0,8
12
x1 0,7
10
x1 0,6
8
x1 0,5
6
x1 0,4
4
2
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x2

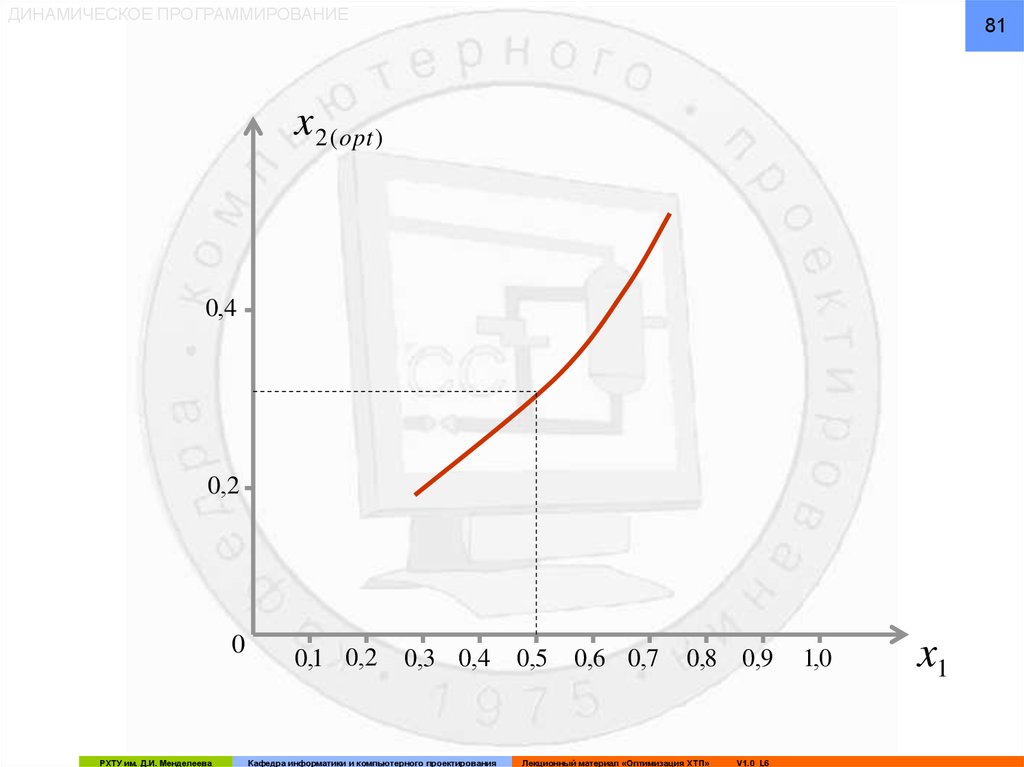
81.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
81
x 2 ( opt )
0,4
0,2
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x1

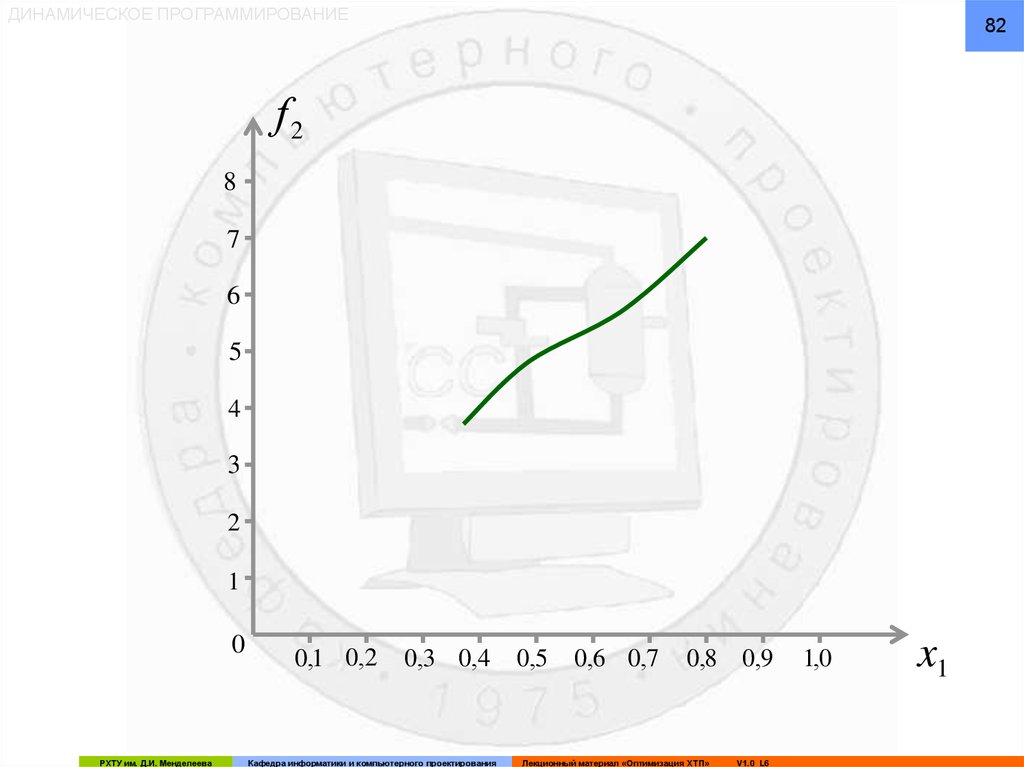
82.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
82
f2
8
7
6
5
4
3
2
1
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x1

83.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
83
Записываем рекуррентное соотношение для f2:
x0 x1
f 3 ( x0 ) min
f
2
2
x1 x
k
x
1
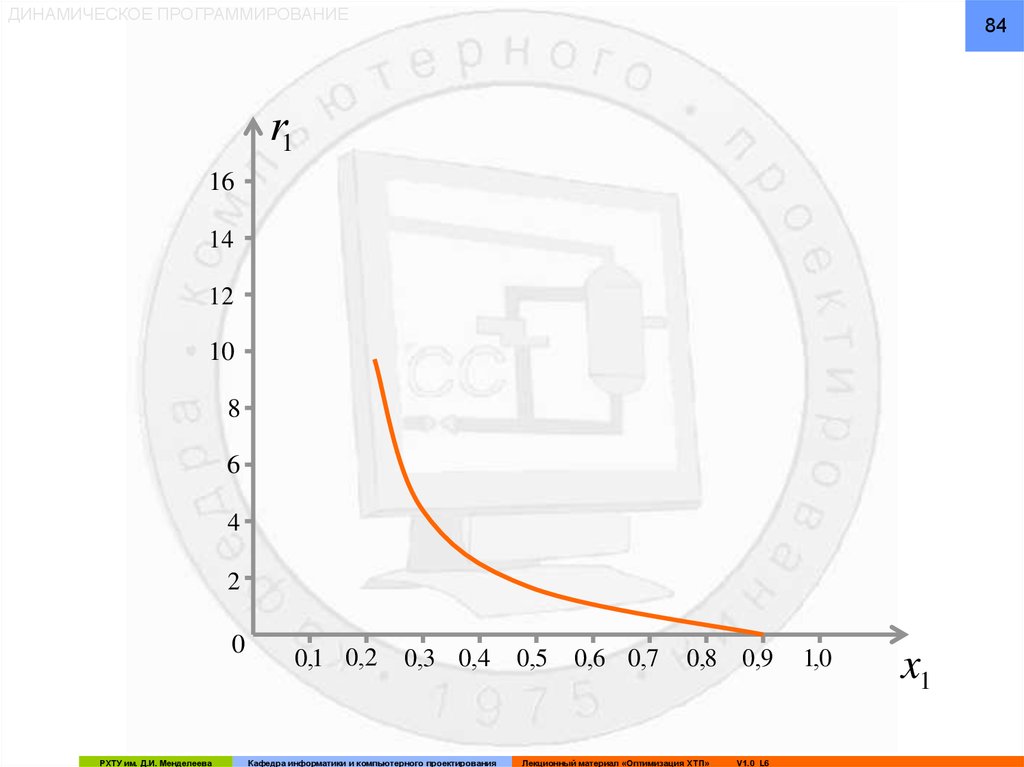
x0 x1
r1
2
k x1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

84.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
84
r1
16
14
12
10
8
6
4
2
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x1

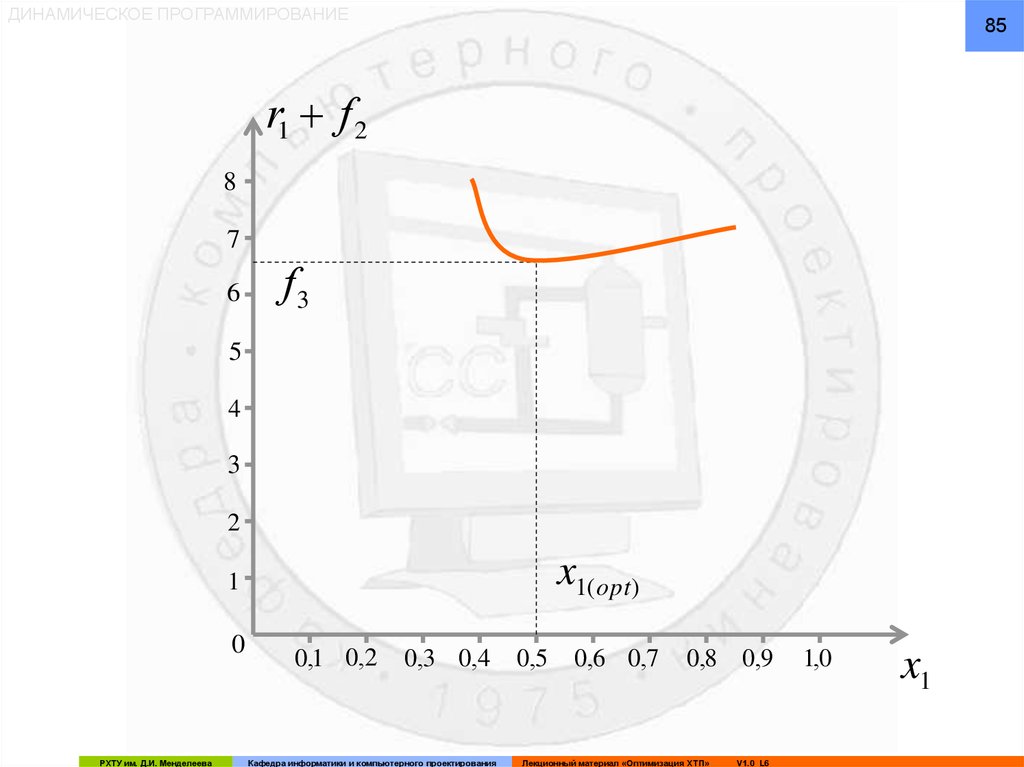
85.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
85
r1 f 2
8
7
6
f3
5
4
3
2
x1( opt)
1
0
РХТУ им. Д.И. Менделеева
0,1 0,2
0,3 0,4
Кафедра информатики и компьютерного проектирования
0,5
0,6 0,7
0,8 0,9
Лекционный материал «Оптимизация ХТП»
V1.0 L6
1,0
x1

86.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
86
Второй этап решения
Из графических построений определяется:
f 3 R min (r1 f 2 ) 6,5 часа
x1 x
И оптимальное управление, соответствующее f3:
x1( opt) 0,5 моль / литр
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

87.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
87
По найденному значению x1(opt) графически определяем x2(opt):
x2( opt) 0,3 моль / литр
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

88.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
88
Рассчитываем время пребывания в каждом из аппаратов:
1
( o p t)
x0 x1( o p t)
k x
2
1( o p t)
1 0,5
2 часа
1 0,25
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

89.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
2
( o p t)
89
x1( o p t) x2( o p t)
k x
2
2 ( o p t)
0,5 0,3
2,2 часа
1 0,09
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

90.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
3( opt)
90
x 2( opt) x3
k x
2
3
0,3 0,2
2,5 часа
1 0,04
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6

91.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
91
3
R τ τ i 6,7 часа
i 1
Небольшое расхождение τ = 6,7 часа с f3 = 6,5 часа
объясняется погрешностью графического расчёта.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L6