Similar presentations:
Построение эмпирических статистических моделей химико-технологических процессов (ХТП)
1.
1Тема
02Построение
: Построение эмпирических статистических моделей ХТП
Тема
02.
эмпирических статистических моделей ХТП
Представление ХТП для построения
математической модели
y1
x1
Объект
y
xr
Объект = «черный ящик» или «black box» - эмпирическая модель
Объект ≠ «черный ящик» или «black box» - физико-химическая модель
y f (x )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
2.
2 Тема 02: Построение эмпирических статистических моделей ХТПI.Принципы построения теоретических
физико-химических моделей
Последовательные этапы
Изучается теория процесса
Составляется система уравнения математического
описания (МО)
Выбирается алгоритм решения системы уравнений
МО, т.н. моделирующий алгоритм (МА)
МА реализуется на компьютере и получается
математическая модель (ММ)
Проверяется адекватность модели путем сравнения
расчетных результатов с экспериментальными
В случае отсутствия адекватности модели решается
задача идентификации,
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
3.
3 Тема 02: Построение эмпирических статистических моделей ХТПv1 C p1
0
T1
0
T2
v2 C p 2
T1
T2
FT KT
Для упрощения построения математического описания рассматриваемого
процесса принимаются следующие допущения
• рассматривается стационарный режим теплопередачи
• оба потока теплоносителей описываются моделью идеального смешения
• происходит только процесс теплопередачи
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
4.
4 Тема 02: Построение эмпирических статистических моделей ХТП(0)
1
(0) (0)
p1 1
1. v C T
v1C p1T1 F q 0
T
T
1
2. q K T2 T1
T
1
( 0)
2
T
( 0) ( 0)
p2 2
3. v C T
v2C p 2T2 F q 0
T
4. q K T1 T2
T
2
T
q q q
T
РХТУ им. Д.И. Менделеева
T
1
Кафедра информатики и компьютерного проектирования
T
2
T
2
5.
5 Тема 02: Построение эмпирических статистических моделей ХТП(0)
1
(0) (0)
p1 1
v1C p1T1 F q 0
( 0)
2
( 0) ( 0)
p2 2
v2C p 2T2 F q 0
1. v C T
2. v C T
T
T
T
T
3. q K T2 T1
T
T
Принимается допущение о том, что константа теплопередачи через поверхность
теплообмена постоянна (KT = const)
Это означает, что теплоёмкости потоков постоянны и не зависят от температуры
В качестве определяемых переменных выбираем температуры потоков на
выходе из теплообменника Т1 и Т2 и локальную интенсивность теплопередачи
ΔqT
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
6.
6 Тема 02: Построение эмпирических статистических моделей ХТППреобразуем систему путём подстановки в уравнения 1 и 2 выражения для
локальной интенсивности теплопередачи ΔqT:
1.
v C T
F K T F K T
T
1
T
T
p1 1
1
2
a12
a11
2.
T
T
T
1
a21
2
T
p2
2
v C T
a22
A x b;
a11 a12 T1 b1
a
21 a22 T2 b2
РХТУ им. Д.И. Менделеева
(0) (0)
p1 1
b1
F K T
v C F K T
T
v C T
(0)
1
Кафедра информатики и компьютерного проектирования
( 0)
2
( 0) ( 0)
p2 2
b2
7.
7 Тема 02: Построение эмпирических статистических моделей ХТПМетодом обратной матрицы находим значения температур потоков на выходе из
теплообменника:
1
T1 a11 a12 b1
T a
2 21 a22 b2
Таким образом определяются температуры потоков Т1 и Т2 на выходе из
теплообменника.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
8.
8 Тема 02: Построение эмпирических статистических моделей ХТПСхематическое представление теплообменника при построении
эмпирической модели
0
T1
T1
v1
0
T2
v2
T2
Принимаются допущения:
0
v1 v1
0
v2 v2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
9.
9 Тема 02: Построение эмпирических статистических моделей ХТПОсновная задача при построении эмпирической модели
теплообменника
На основании обработки экспериментальных данных о функционировании
теплообменника получить две функциональные зависимости следующего вида:
0
0
0
0
T1 f1 (T1 , v1 , T2 , v2 , a1 )
T2 f 2 (T1 , v1, T2 , v2 , a2 )
Где
a1 , a2
- коэффициенты функциональных зависимостей
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
10.
10 Тема 02: Построение эмпирических статистических моделей ХТПВ общем случае:
y f ( x, a )
y1 T1
y
y2 T2
где
x1 T1
x
v
2
1
x
0
x3 T2
x4 v 2
a - коэффициенты функциональных зависимостей:
y1 f1 ( x , a1 )
y2 f 2 ( x , a2 )
РХТУ им. Д.И. Менделеева
0
Кафедра информатики и компьютерного проектирования
11.
11 Тема 02: Построение эмпирических статистических моделей ХТПII. Принципы построения эмпирических моделей
по данным пассивных экспериментов
Последовательные этапы
Проведение экспериментальных исследований
Выбор вида зависимостей выходных переменных Y от
вектора входных переменных Х
Определение коэффициентов уравнений,
описывающих зависимости каждой выходной
переменной от всех входных переменных Х
Регрессионный и корреляционный анализ
экспериментальных данных, по которым были
построены эмпирические модели
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
12.
12 Тема 02: Построение эмпирических статистических моделей ХТПII.1. Проведение экспериментальных исследований
Различают пассивный и активный эксперимент
Теория активного эксперимента позволяет оптимизировать
экспериментальные исследования и установить:
•количество экспериментальных измерений
•при каких значениях входных переменных надо проводить опыты
•реализовать эффективную методику обработки экспериментальных даных
•сократить число экспериментальных исследований
•обеспечивать достижение требуемых целей экспериментальных исследований
В пассивном эксперименте указанные параметры экспериментальных
исследований определяются опытом, эрудицией и интуицией исследователя.
При этом различают:
•лабораторный пассивный эксперимент – планируемый и целенаправленный
•промышленный пассивный эксперимент – наблюдаемый при протекании
технологических процессов
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
13.
13 Тема 02: Построение эмпирических статистических моделей ХТПРезультаты исследований при пассивном эксперименте представляются в виде таблицы
экспериментов:
число
x1
x2
xr
y1э
y 2э
y э
1
x11
x12
x1r
y11э
y12э
y1 э
2
x21
x22
x2 r
э
y21
э
y22
э
y 2
n
xn1
xn 2
xnr
ynэ1
y nэ 2
ynэ
x, y
№
где n – число экспериментов
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
14.
14 Тема 02: Построение эмпирических статистических моделей ХТПТаблица проведения экспериментальных исследований для одной выходной
э
переменной y имеет вид:
p
x1
x2
xr
yэ
1
x11
x12
x1r
y1э
2
x21
x22
x2 r
y 2э
n
xn1
xn 2
xnr
ynэ
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
15.
15 Тема 02: Построение эмпирических статистических моделей ХТПII.2. Выбор вида зависимости выходной переменной y от входной
переменной x
Для этой цели анализируется следующая таблица экспериментов:
№
1
2
n
x
x1
x2
xn
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
э
y
э
y1
э
y2
э
yn
16.
16 Тема 02: Построение эмпирических статистических моделей ХТПII.2.1. Определение вида приближённого уравнения регрессии
В общем случае необходимо анализировать графики зависимостей
экспериментальных данных выходных переменных y от входных x и по их виду
выбирать конкретную форму приближенного уравнения регрессии.
Для случая одной входной переменной х по опытным данным рекомендуется
построить эмпирическую линию регрессии и с её помощью выбирать вид
приближенного уравнения регрессии.
Y
y j
xj
x j
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
X
17.
17 Тема 02: Построение эмпирических статистических моделей ХТППри этом весь диапазон изменения x разбивается на s равных интервалов Δx.
Все точки, попавшие в данный интервал x j , относят к его середине x j .
После этого подсчитывают частные средние y j для каждого интервала:
nj
j
y
y
i 1
nj
ji
, j 1,...s
n j число точек в интервале x j .
В результате объём выборки определяется по формуле:
s
n
j 1
РХТУ им. Д.И. Менделеева
j
n
Кафедра информатики и компьютерного проектирования
18.
18 Тема 02: Построение эмпирических статистических моделей ХТПЭмпирическая линия регрессии y от x получается в виде ломанной линии
путём последовательного соединения отрезками прямой линии точек:
x , y ,
j
j
j 1,...s
При выборе вида приближенного уравнения регрессии для случая нескольких входных
переменных
x x1 ,...xm
T
может быть применён метод Брандона, который здесь не рассматривается.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
19.
19 Тема 02: Построение эмпирических статистических моделей ХТПII.3. Определение коэффициентов уравнения регрессии –
параметров эмпирических моделей методом наименьших
квадратов
В соответствии с методологией регрессионного анализа в этом случае решается
задача аппроксимации экспериментальных данных методом наименьших
квадратов (МНК)
При этом предполагается, что вид уравнения регрессии или уравнение
эмпирической модели известно, т.е. решена задача структурной
идентификации модели.
Задача параметрической идентификации модели, т.е. определения
коэффициентов модели решается по МНК
Задачи структурной и параметрической идентификации моделей связаны
между собой и неудовлетворительное решение одной из них может приводить к
необходимости пересмотра результатов решения другой.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
20.
20 Тема 02: Построение эмпирических статистических моделей ХТПВ общем случае возможны два варианта:
а) нелинейная относительно коэффициентов a модель – нелинейная регрессия
yˆ f ( x , a )
б) линейная относительно коэффициентов a модель – линейная регрессия
m
yˆ a j j x
j 0
j x
- линейные или нелинейные функции входных переменных
a a0 , a1, ... am - определяемые по МНК коэффициенты модели
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
21.
21 Тема 02: Построение эмпирических статистических моделей ХТППреимущества линейных моделей
1. Относительно несложная методика выбора вида модели
2. Простая процедура определения коэффициентов модели
3. Эффективная методика регрессионного и корреляционного анализа
Поэтому нелинейные модели, по возможности, стараются линеаризовать,
т.е. привести к линейному виду.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
22.
22 Тема 02: Построение эмпирических статистических моделей ХТПЛинеаризация уравнения Аррениуса
k Ae
E RT
E 1
ln k ln A
R T
yˆ a0 0 ( x ) a1 1 ( x ), ãäåm 1
При этом:
yˆ ln k
a0 ln A
E
a1
R
0 ( x ) 1
1
1 ( x )
T
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
23.
23 Тема 02: Построение эмпирических статистических моделей ХТПРазновидности линейных уравнений регрессии
•полиномиальное уравнение регрессия, когда
j x x
j
j 0,1,...m
и её разновидности:
линейное уравнение регрессии от одной переменной (m = 1):
yˆ a0 a1 x
параболическое уравнение регрессии (m = 2):
ˆy a0 a1 x a2 x 2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
24.
24 Тема 02: Построение эмпирических статистических моделей ХТП•трансцендентные уравнения регрессии и их разновидности в виде
зависимостей:
yˆ a0 a1
показательного типа:
x
ln yˆ ln a0 x ln a1
которая линеаризуется логарифмированием:
yˆ a0 x
дробно-показательного типа:
a1
которая также линеаризуется логарифмированием:
ln yˆ ln a0 a1 ln x
•множественное уравнение регрессии, когда число входных переменных
больше 1:
yˆ a0 a1 x1 ... am xm
x0 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
25.
25 Тема 02: Построение эмпирических статистических моделей ХТПОпределение коэффициентов эмпирических моделей методом
наименьших квадратов (МНК)
Для линейных и нелинейных моделей минимизируется критерий
рассогласования расчетных и экспериментальных данных следующего вида:
n
Cr y y
где y
p
i и
p
i
2
i
i 1
y определяются при одном и том же значении элементов вектора
i
xi i 1,...n
n – общее число опытов (объём выборки).
При этом определяются оптимальные значения коэффициентов a , которые
обеспечивают наименьшее (в частном случае – минимальное) значение
критерия Cr
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
26.
26 Тема 02: Построение эмпирических статистических моделей ХТПГрафическая иллюстрация метода наименьших квадратов (МНК)
Для случая регрессии одной переменной y от х и уравнения линейной регрессии
с двумя коэффициентами:
yˆ a0 a1 x
y
y np
ynэ
y1э
y1p
x1
РХТУ им. Д.И. Менделеева
xn
Кафедра информатики и компьютерного проектирования
x
27.
27 Тема 02: Построение эмпирических статистических моделей ХТПДля линейных и нелинейных уравнений регрессии с m + 1 коэффициентами:
a a0 , a1 ,... am
T
критерий МНК также является функцией многих переменных от параметров a
Cr Cr a0 , a1 ,... am
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
28.
28 Тема 02: Построение эмпирических статистических моделей ХТПДля определения (подгонки) коэффициентов (параметров) модели необходимо,
чтобы критерий МНК стал наименьшим.
Задача определения коэффициентов нелинейных моделей сводится к
реализации одного из алгоритмов оптимизации для определения минимума
критерия МНК:
n
min
y y
доп
a a
i 1
i
p
i
2
a доп - допустимая область изменения параметров a - ограничения первого
рода.
В этом случае для определения коэффициентов необходимо реализовать
алгоритм оптимизации, позволяющий найти наименьшее значение критерия:
n
Cr a0 , a1 ,... am ( y y )
p
i
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
э 2
i
29.
29 Тема 02: Построение эмпирических статистических моделей ХТПЗадача определения коэффициентов линейных моделей сводится к решению
системы линейных алгебраических уравнений (СЛАУ), исходя из необходимого
условия экстремума функции многих переменных
n
Cr a0 , a1 ,... am ( y y )
p
i
э 2
i
i 1
то есть СЛАУ, решаемая относительно коэффициентов:
a a0 , a1 ,... am
T
имеет вид:
Cr
0;
a0
РХТУ им. Д.И. Менделеева
Cr
Cr
0; ...
0
a1
am
Кафедра информатики и компьютерного проектирования
30.
30 Тема 02: Построение эмпирических статистических моделей ХТПВывод формулы для определения коэффициентов линейных и
линеаризованных моделей
Матричная формула определения коэффициентов имеет вид:
1
ˆa y
T
РХТУ им. Д.И. Менделеева
T
Кафедра информатики и компьютерного проектирования
31.
31 Тема 02: Построение эмпирических статистических моделей ХТПгде матрица
Ф
- это матрица вида
0 x1 1 x1
x x
1
2
0 2
n m 1
...
...
0 xn 1 xn
... m x1
... m x2
...
...
... m xn
элементы которой зависят от экспериментальных значений входных
переменных и вида функций x ;
э
вектор y - это вектор наблюдений экспериментальных значений выходной
переменной
э
В случае линеаризации моделей элементы матрицы Ф и вектора y
определяются из выражений, соответствующих выбору способа линеаризации.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
32.
32 Тема 02: Построение эмпирических статистических моделей ХТПДля вывода этой формулы критерий МНК необходимо представить в виде:
m
Cr a j j xi yi
i 1 j 0
n
2
и, воспользовавшись необходимым условием экстремума функции многих
переменных, решать полученную систему линейных алгебраических уравнений
(СЛАУ):
n
m
Cr
2 a j j xi yi 0 xi 0
a0
i 1 j 0
n m
Cr
2 a j j xi yi 1 xi 0
a1
i 1 j 0
..............................................................
n m
Cr
2 a j j xi yi m xi 0
am
i 1 j 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
33.
33 Тема 02: Построение эмпирических статистических моделей ХТППерегруппировав члены в последней системе уравнений, можно записать СЛАУ
в виде:
m
n
n
j 0
i 1
i 1
a
x
x
x
y
j j i u i u i i
( j , u 0,1,...m)
И, если ввести в рассмотрение информационную матрицу
uj
n
j 0,1,...m; u 0,1,...m :
uj u xi j xi
j 0,1,...m; u 0,1,...m
i 1
то она окажется квадратной, симметричной и значения её элементов зависят
только от входных переменных и конкретного вида функций j x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
34.
34 Тема 02: Построение эмпирических статистических моделей ХТПВ матричном виде информационную матрицу можно представить в виде
произведения транспонированной и исходной матрицы входных переменных :
T
Матрица, зависящая от входных переменных, имеет вид:
0 x1 1 x1
x x
0
2
1
2
n m 1
...
...
0 xn 1 xn
... m x1
... m x2
...
...
... m xn
Соответственно правую часть рассматриваемой СЛАУ можно записать:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
35.
35 Тема 02: Построение эмпирических статистических моделей ХТПn
bu u xi yi
(u 0,1,...m)
i 1
или в матричном виде:
T
b y
В результате СЛАУ, решаемая для определения коэффициентов эмпирической
модели, может быть представлена:
m
j 0
uj
a j bu
(u 0,1,...m)
или в матричном виде:
a b
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
36.
36 Тема 02: Построение эмпирических статистических моделей ХТПЕсли для определения коэффициентов использовать метод обратной матрицы,
то получится:
1
1
a b
1
,
1
a b,
1
a b
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
37.
37 Тема 02: Построение эмпирических статистических моделей ХТПМатричная формула для определения коэффициентов линейной регрессии
(параметров эмпирической модели):
1
ˆa y
T
T
Таким образом, для определения коэффициентов линейной или
линеаризованной регрессионной модели необходимо выполнить следующую
последовательность действий:
• сформировать вектор наблюдений
линеаризованных моделей);
y и вычислить его компоненты (только для
• сформировать и рассчитать компоненты матрицы, зависящей от входных переменных
;
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
38.
38 Тема 02: Построение эмпирических статистических моделей ХТП• транспонировать матрицу
T
;
• перемножить транспонированную матрицу
T
на исходную матрицу
:
T
;
• выполнить обращение информационной матрицы -
T
;
• умножить полученную обратную матрицу на матрицу
• умножить полученный результат на вектор наблюдений
коэффициенты регрессии
â
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
;
1
T
и yполучить выборочные
39.
39 Тема 02: Построение эмпирических статистических моделей ХТПII.4. Регрессионный и корреляционный анализ экспериментальных
данных, по которым были построены эмпирические модели
II.4.1. Статистический анализ полученной линейной или
линеаризованной модели
m
yˆ aˆ j j x
j 0
Определение коэффициентов линейной или линеаризованной модели методом
аппроксимации (конкретно МНК) выполняется по матричной формуле:
1
T
aˆ y
T
где значения элементов матрицы независимых переменных зависят только от
:x
входных переменных
иx вида функций
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
40.
40 Тема 02: Построение эмпирических статистических моделей ХТП0 x1 1 x1
x x
1 2
0 2
n m 1
...
...
0 xn 1 xn
... m x1
... m x2
...
...
... m xn
Вектор наблюдений y является случайным вектором, т.к.:
• определен по случайной выборке (статистике)
• экспериментальные значения компонентов этого вектора в общем случае
являются случайными величинами
В соответствии с приведенной линейной матричной формулой компоненты
результирующего вектора â - коэффициентов модели также являются
случайными величинами и вектор â является случайным вектором
Поэтому для анализа линейной модели следует применить один из методов
статистического анализа – регрессионный анализ
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
41.
41 Тема 02: Построение эмпирических статистических моделей ХТПII.4.1.1. Условия применимости регрессионного анализа
• входные переменные x измеряются с пренебрежимо малой ошибкой и
являются детерминированными (неслучайными) величинами
э
• результаты наблюдений выходной переменной y представляют собой
реализации независимых нормально-распределённых случайных величин
• при проведении экспериментов с объёмом выборки п при условии, что каждый
опыт повторён несколько раз, оценки дисперсий случайных величин Y ,
полученные по различным выборкам, являются однородными. Свойство
однородности предполагает несущественное отличие дисперсий Y , что
позволяет усреднять их оценки или значения, полученные по ограниченным
выборкам, и распространять на всю исследуемую область, и проверяется с
помощью специальных критериев, которые здесь не рассматриваются.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
42.
42 Тема 02: Построение эмпирических статистических моделей ХТПII.4.1.1.2. Этапы регрессионного анализа
Регрессионный анализ проводится после того, как определён вид уравнения
регрессии и заключается в следующем:
1. Определение коэффициентов модели – коэффициентов регрессии по
экспериментальным данным методом наименьших квадратов
2. Определение значимости коэффициентов регрессии с использованием t –
распределения Стьюдента и реализация процедуры отсеивания незначимых
коэффициентов модели
3. Определение адекватности уравнения регрессии с использованием F –
распределения Фишера
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
43.
43 Тема 02: Построение эмпирических статистических моделей ХТПII.4.1.1.3. Числовые характеристики компонентов случайных
векторов наблюдений и коэффициентов регрессии
Связь случайных векторов Y и a реализациями которых являются
соответственно y э и â , полученные из данных экспериментальных
измерений
Вектор коэффициентов модели (вектор коэффициентов регрессии) â
присутствует в уравнении для линейной модели:
m
yˆ aˆ j j x ,
j 0
э
а вектор экспериментальных значений (вектор наблюдений) y присутствует в
матричном соотношении:
1
T
aˆ y
T
в качестве линейного сомножителя.
Поэтому целесообразно ввести матрицу
L
1
T
L
T
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
44.
44 Тема 02: Построение эмпирических статистических моделей ХТППосле чего матричную формулу МНК для определения коэффициентов модели
можно записать:
â L y
В соответствии со свойством линейности закона нормального распределения
(компоненты случайного вектора
Y, реализациями которого являются
э
компоненты вектора наблюдений y распределены по закону нормального
распределения) компоненты вектора коэффициентов регрессии также будут
нормально-распределенными случайными величинами.
Известно, что функция плотности распределения произвольной случайной
величины Yi (i 1, ..., n) имеет вид:
f Yi
1
Y
i
РХТУ им. Д.И. Менделеева
1 Yi mYi
exp
2 Y2
2
i
Кафедра информатики и компьютерного проектирования
i 1,...n,
45.
45 Тема 02: Построение эмпирических статистических моделей ХТПи числовыми характеристиками случайной величины Yi будут:
mYi - математическое ожидание
Y2
i
- дисперсия
Y Y2
i
i
- среднеквадратичное отклонение или стандарт.
В соответствии с вышеизложенным для нормально-распределенных случайных
величин наблюдений yi (i 1, ..., n) и коэффициентов a j ( j 0, 1, ..., m)
справедливы следующие числовые характеристики:
m yi ;
;
2
yi
ma j
- математическое ожидание
a2
- дисперсия
j
2
y y2 ; a a
i
i
(i 1, ..., n)
j
j
- среднеквадратичное отклонение или стандарт.
( j 0, 1, ..., m)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
46.
46 Тема 02: Построение эмпирических статистических моделей ХТПОпределение теоретического и эмпирического уравнения регрессии
С использованием числовых характеристик, в частности математического
ожидания Y можно получить строгую зависимость случайной величины
значений входных переменных x .
Y от
Для этой цели применяется зависимость условного математического ожидания
mY от значений входных переменных x , называемое теоретическим
x
уравнением регрессии:
m
mY a j j x
x
j 0
где
a j ( j 0, 1, ..., m) -истинные значения коэффициентов регрессии, называемых
теоретическими коэффициентами регрессии;
m y mY
x
-условное математическое ожидание случайной величины Y.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
47.
47 Тема 02: Построение эмпирических статистических моделей ХТПЭмпирическое уравнение регрессии или регрессионная модель с
соответствующими эмпирическими коэффициентами имеет известный вид
m
yˆ aˆ j j x
j 0
или в матричном виде:
yˆ aˆ
Определение числовых характеристик случайных величин Y измерений
выходной переменной и их корреляционный анализ
- вектор математических ожиданий
my M Y
x
Для дисперсий yi и y j справедливо:
M yi my
2
yi
РХТУ им. Д.И. Менделеева
i
2
Кафедра информатики и компьютерного проектирования
i 1,...n
48.
48 Тема 02: Построение эмпирических статистических моделей ХТПКовариация двух случайных величин равна математическому ожиданию
произведения Yi my Y j my
i
j
COV yi y j M Yi m yi Y j m y j
i 1,...n;
j 1,...n; i j
Для независимых нормально - распределённых случайных величин Yi и Y j
COV yi y j 0
Для нормально-распределённых случайных величин вместо размерной
величины COV yi y j целесообразно пользоваться коэффициентом корреляции:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
49.
49 Тема 02: Построение эмпирических статистических моделей ХТПryi y j
COV yi y j
y y
i
i 1,...n;
j
Для линейно-зависимых случайных величин yi и y j
ryi y j 1
А для независимых -
РХТУ им. Д.И. Менделеева
ryi y j 0
Кафедра информатики и компьютерного проектирования
j 1,...n
50.
50 Тема 02: Построение эмпирических статистических моделей ХТПY
Слабая отрицательная корреляция
между Х и Y
rxy 0.3
X
Y
Сильная положительная корреляция
между Х и Y
rxy 0.9
X
Y
Отсутствие корреляции между Х и Y
rxy 0
X
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
51.
51 Тема 02: Построение эмпирических статистических моделей ХТПВыборочный коэффициент корреляции вычисляется по формуле:
n
rˆXY
( x mˆ
i 1
i
X
)( yi mˆ Y )
(n 1) S X SY
где
1
mˆ X xi
n i 1
1 n
2
ˆ
SX
( xi mX )
n 1 i 1
1 n
mˆ Y yi
n i 1
1 n
2
ˆ
( yi mY )
n 1 i 1
n
РХТУ им. Д.И. Менделеева
SY
Кафедра информатики и компьютерного проектирования
52.
52 Тема 02: Построение эмпирических статистических моделей ХТПДля дисперсий y в n экспериментальных точках создаётся матрица
дисперсий – ковариаций:
2
COVy M y my y my
2
M y1 m y1
M y m y m
n
yn
1
y1
РХТУ им. Д.И. Менделеева
T
M y1 m y1 y2 m y2
M yn m yn y2 m y2
Кафедра информатики и компьютерного проектирования
M y1 m y1 yn m yn
2
M yn m yn
53.
53 Тема 02: Построение эмпирических статистических моделей ХТПВ результате матрица дисперсий - ковариаций имеет вид:
y21
COV y2 y1
COV y
COV yn y1
COV y1 y2
y2
2
COV yn y2
COV y1 yn
COV y2 yn
2
yn
Если принять два допущения:
COV
0 i j
о независимости измерений
2
об однородности дисперсии, т.е. несущественном отличии yi и их равенстве
yi y j
y2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
54.
54 Тема 02: Построение эмпирических статистических моделей ХТПто получается диагональная матрица дисперсий - ковариаций для измеряемых
y
значений
с одинаковыми дисперсиями y2
COVy E
2
y
Определение числовых характеристик случайных величин коэффициентов
регрессии и их корреляционный анализ
Поскольку a - случайная величина, распределённая по нормальному закону,
ma M a .
По аналогии составим матрицу дисперсий-ковариаций для a :
COVa M a ma a ma
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
T
55.
55 Тема 02: Построение эмпирических статистических моделей ХТПa20
COV a1a0
COV am a0
COV a0 a1
a2
1
COV am a1
COV a0 am
COV a1am
2
am
В соответствии с формулой для оценок коэффициентов уравнения регрессии
a Ly
ma Lm y
Для определения элементов матрицы дисперсий-ковариаций необходимо
подставить два последних выражения в матричную формулу
Если в результате подстановки матрица дисперсий - ковариаций получится
диагональной, то коэффициенты регрессии можно считать статистически
независимыми
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
56.
56 Тема 02: Построение эмпирических статистических моделей ХТПВыполним эту подстановку
T
T
COVa M L y Lmy L y Lmy M L y my L y my
T
T
M L y m y y m y L
LM y m y y m y L LCOV y L
T
1
T
T
Lσ 2y E L σ 2y
T
T
T
E
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
T
1
57.
57 Тема 02: Построение эмпирических статистических моделей ХТПT
1
Поскольку COV y σ E , а матрица ( ) симметрична,
2
y
COV a σ
2
y
T
1
T
1
Назовём обратную матрицу ( ) корреляционной матрицей
C 00
C
1
T
10
C
C m 0
РХТУ им. Д.И. Менделеева
C 01 C 0 m
C11 C1m
.
C m1 C mm
Кафедра информатики и компьютерного проектирования
58.
58 Тема 02: Построение эмпирических статистических моделей ХТПТогда
C 00 C 01
C
C11
2
2 10
COVa σ y C σ y
C m 0 C m1
C 0 m σ 2a0
C1m COVa1a0
C mm COVam a0
COVa0a1 COVa0am
σ 2a1
COVa1am
2
COVam a1
σ am
откуда следует:
• для дисперсий коэффициентов регрессии
σ σ C jj ,
2
aj
2
y
j 0, 1, ..., m
• для ковариаций коэффициентов регрессии
COVa j ai σ C ji ,
2
y
РХТУ им. Д.И. Менделеева
j , i 0, 1, ..., m; i j
Кафедра информатики и компьютерного проектирования
59.
59 Тема 02: Построение эмпирических статистических моделей ХТПТаким образом, независимость коэффициентов определяется тем, будут ли
недиагональные элементы в матрице корреляции C равны нулю.
Значения элементов этой матрицы определяются экспериментальными
величинами x и видом функций x , т.е. зависят от того, как поставлен
(спланирован) эксперимент.
В случае активного эксперимента (например, полного факторного
эксперимента – ПФЭ и ортогонального центрального композиционного плана
эксперимента - ОЦКП) его проводят так, чтобы матрица C стала диагональной,
т.е. чтобы коэффициенты регрессии были статистически независимы.
В случае произвольного пассивного эксперимента матрица C оказывается
недиагональной и поэтому коэффициенты будут статистически зависимы.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
60.
60 Тема 02: Построение эмпирических статистических моделей ХТПМатрица C называется корреляционной, т.к. с помощью её элементов можно
рассчитать корреляции коэффициентов регрессии:
ra j ai
РХТУ им. Д.И. Менделеева
C ji
C jjCii
Кафедра информатики и компьютерного проектирования
61.
61 Тема 02: Построение эмпирических статистических моделей ХТП2
II.5. Определение оценок дисперсии y
2
Определяются три типа оценок дисперсий y :
S R2 - остаточная дисперсия, характеризующая погрешности экспериментов и
модели (уравнения регрессии);
Se2 - дисперсия воспроизводимости, характеризующая погрешности
экспериментов;
S ad2 - дисперсия адекватности, характеризующая погрешность модели
(уравнения регрессии)
Для определения указанных оценок дисперсий проводятся
экспериментальные исследования и расчеты по регрессионным моделям
Пусть выходная переменная y зависит от r входных переменных (независимых
переменных x ).
Для оценки дисперсии проводятся два типа экспериментов:
С изменением независимых переменных x1 , ..., xn ;
Параллельные опыты, когда независимые переменные не меняются.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
62.
62 Тема 02: Построение эмпирических статистических моделей ХТП2
2
2
Определение оценок дисперсий S R , Se , S ad в экспериментах с изменением
независимых переменных с различным числом параллельных опытов в каждой
точке (ki, i=1, …, n)
а) Определение остаточной дисперсии S R2
x, y
yэ
x1
xr
1 k1
x11 x11
x1r x1r
1 k n
xn1 xn1
xnr xnr
ynэ1 ynkэ n
n
yˆ y
n
S
2
R
ki
i 1
РХТУ им. Д.И. Менделеева
i
i 1 u 1
n
k
ý 2
iu
i
p
SS R
fR
Кафедра информатики и компьютерного моделирования
э
y11
y1эk1
63.
63 Тема 02: Построение эмпирических статистических моделей ХТПгде
р - число значимых коэффициентов регрессии
S R2 - остаточная дисперсия - характеризует погрешности уравнений (или моделей)
и погрешности экспериментов;
ŷ -определяются с помощью коэффициентов по уравнению регрессии;
y э - экспериментальные значения;
SS R - сумма квадратов остаточной дисперсии;
f R - число степеней свободы остаточной дисперсии;
n - число опытных измерений;
k i - число параллельных опытов в i – ой экспериментальной точке
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
64.
64 Тема 02: Построение эмпирических статистических моделей ХТПОстаточная сумма квадратов SS R равна сумме квадратов дисперсии
адекватности SS ad , характеризующей погрешность уравнения регрессии и
сумме квадратов дисперсии воспроизводимости SSe , характеризующей
погрешность экспериментов.
SS R SS ad SSe
Соответственно для числа степеней свободы остаточной дисперсии
справедливо:
n
f R ki p f ad f e
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
S R2 будет
65.
65 Тема 02: Построение эмпирических статистических моделей ХТПб) Определение дисперсии воспроизводимости Se2 .
2
Дисперсия воспроизводимости Se определяется из параллельных опытов,
когда их число различно в каждой экспериментальной точке и равно ki (i 1,...n) :
y
n
S
2
e
ki
i 1 u 1
n
iu
k
i 1
i
y
1
ki
yi
РХТУ им. Д.И. Менделеева
2
i
y
iu
u 1
ki
Кафедра информатики и компьютерного проектирования
SS e
fe
66.
66 Тема 02: Построение эмпирических статистических моделей ХТП2
в) Определение дисперсии адекватности S ad
В этом случае в соответствии с приведёнными ранее равенствами
S
2
ad
SS ad
f ad
где
SSad SS R SSe
f ad f R f e n p
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
67.
67 Тема 02: Построение эмпирических статистических моделей ХТП2
2
2
Определение оценок дисперсий S R , Se , S ad с одинаковым числом
параллельных опытов в каждой точке (k) с изменением независимых
переменных
а) Определение дисперсии воспроизводимости Se2 .
• Определение дисперсии воспроизводимости S e2i в i – ой экспериментальной
точке
Таблица эксперимента
x, y
xi1
xir
yi
1
xi1
xir
yi 1
k
xi1
xir
yik
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
68.
68 Тема 02: Построение эмпирических статистических моделей ХТП• Значение дисперсии воспроизводимости в i – ой экспериментальной точке
y
k
S
2
ei
j 1
ij
y
2
i
k 1
SS ei
f ei
i 1,...n
k
при этом среднее значение
РХТУ им. Д.И. Менделеева
yi
y
ij
j 1
k
Кафедра информатики и компьютерного проектирования
i 1,...n
69.
69 Тема 02: Построение эмпирических статистических моделей ХТПS e2i -дисперсия воспроизводимости – характеризует погрешность эксперимента в
i-ой опытной точке;
yij - экспериментальные значения, полученные в параллельных опытах в i-ой
точке;
yi - усреднённое экспериментальное значение в i-ой точке;
SS ei - сумма квадратов дисперсии воспроизводимости в i-ом эксперименте;
f ei k 1 - число степеней свободы дисперсии воспроизводимости в i-ой
точке;
k - число параллельных опытов в i-ой экспериментальной точке.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
70.
70 Тема 02: Построение эмпирических статистических моделей ХТП• Значение дисперсии воспроизводимости для n экспериментальных точках
В соответствии со свойством однородности дисперсии воспроизводимости для n
экспериментальных точек
y
n
S
2
e
k
i 1 j 1
ij
2
i
y
n k 1
n
т.к.
S e2
2
S
ei
i 1
n
РХТУ им. Д.И. Менделеева
и
f e n k 1 .
Кафедра информатики и компьютерного проектирования
SSe
fe
71.
71 Тема 02: Построение эмпирических статистических моделей ХТП2
б) Определение дисперсии адекватности S ad
S
2
ad
2
k yi yi
SS ad
i 1
n p
f ad
n
k
при этом среднее значение
РХТУ им. Д.И. Менделеева
yi
y
iu
u 1
k
Кафедра информатики и компьютерного проектирования
i 1,...n
72.
72 Тема 02: Построение эмпирических статистических моделей ХТП2
в) Определение остаточной дисперсии S R
yˆ y
n
S
2
R
k
ý 2
iu
i
i 1 u 1
n
k p
SSR
fR
i 1
n
k
SSR yˆ i y
где
i 1 u 1
f R nk p
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
ý 2
iu
73.
73 Тема 02: Построение эмпирических статистических моделей ХТП2
2
2
Определение оценок дисперсий S R , Se , S ad , когда параллельные опыты
проведены в отдельно взятой точке
а) Определение дисперсии воспроизводимости Se2 .
y
k
S
2
e
u 1
ju
yj
2
k 1
SSe
fe
k
при этом среднее значение
y
j
y
ju
u 1
k
Для одинакового числа параллельных опытов в каждой экспериментальной
точке ( k ) дисперсия адекватности определяется:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
74.
74 Тема 02: Построение эмпирических статистических моделей ХТП2
2
б) Определение остаточной дисперсии S R и дисперсии адекватности S ad
2
S R2 S ad
РХТУ им. Д.И. Менделеева
2
yi yi
SS ad SS R
i 1
n p
f ad
fR
n
Кафедра информатики и компьютерного проектирования
75.
75 Тема 02: Построение эмпирических статистических моделей ХТПДля оценки дисперсий наблюдений y а при отсутствии
Se2 параллельных опытов -
ˆ y2
целесообразно
использовать
2
S
.
ad
Для определения оценок дисперсий коэффициентов
σ̂ 2a j σ̂ 2y C jj ,
j 0, 1, ..., m
2
используют оценки ˆ y :
2
а) дисперсию воспроизводимости Se
2
б) остаточную дисперсию S R
2
в) дисперсию адекватности S ad
РХТУ им. Д.И. Менделеева
â j :
Кафедра информатики и компьютерного проектирования
,
76.
76 Тема 02: Построение эмпирических статистических моделей ХТПII.5.2. Определение значимости коэффициентов регрессии.
(Выполнение второго этапа регрессионного анализа)
Для этого используется нормированная случайная величина:
tj
aˆ ma j
ˆ a
j
подчиняющаяся t –распределению Стьюдента.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
,
77.
77 Тема 02: Построение эмпирических статистических моделей ХТПВоспользовавшись оценкой дисперсии
S S C jj
2
aj
2
e
ˆ a S a S
j
j
2
aj
можно записать вероятностное соотношение:
aˆ j ma
j
òàáë.
P
t fe
Se C jj
В этом случае табличное значение t берётся при доверительной вероятности β
(чаще всего 0,95) и числе степеней свободы дисперсии воспроизводимости f e .
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
78.
78 Тема 02: Построение эмпирических статистических моделей ХТПЕсли предположить, что математическое ожидание коэффициента ma j 0 (т.е.
истинное его значение равно нулю), то условие незначимости коэффициента a j
имеет вид:
aˆ j
S e C jj
t
òàáë
fe
Для значимых коэффициентов, раскрывая неравенство, получим следующий
доверительный интервал:
aˆ j Se C t
òàáë
jj f e
ma j aˆ j Se C t
òàáë
jj f e
Это означает, что вместо оценки коэффициентов регрессии a j можно
пользоваться их крайними значениями. Это в свою очередь приведёт к
различным величинам ŷ в уравнении:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
79.
79 Тема 02: Построение эмпирических статистических моделей ХТПm
yˆ aˆ j j x
j 1
В результате на графике вместо одной кривой, полученной по оценочным
значениям коэффициентов регрессии, получается три: одна - минимальных
значений a j , вторая – максимальных значений a j и третья – сплошная, для
оценочных значений коэффициентов регрессии:
y
a min
â
a max
x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
80.
80 Тема 02: Построение эмпирических статистических моделей ХТПt - распределение Стьюдента
Где:
Схема определения квантиля
p 1
v fe
p
2
0,55
0,60
0,65
0,70
0,75
1
0,158
0,325
0,510
0,727
1,000
2
0,142
0,289
0,445
0,617
0,816
3
0,137
0,277
0,424
0,584
0,765
4
0,134
0,271
0,414
0,569
0,741
5
0,132
0,267
0,408
0,559
0,727
\1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
81.
81 Тема 02: Построение эмпирических статистических моделей ХТППример. Определить доверительный интервал, в котором с доверительной
вероятностью 0,95 располагается истинное значение измеряемого параметра, по
результатам восьми титрований х, см3
76,48 76,25 76,43 76,48 77,20 76,48 76,45 76,60
Решение. Имеем функцию распределения Стьюдента:
n
x xi n ; x 76.546 см 3 ; ν 8 1 7
i 1
Из таблиц находим
Рассчитываем
t07.975 2.365
n
S X2 ( xi x ) 2 / ν; S X2 0.5543/ 7 0.079 см3
i 1
Получаем доверительный интервал:
75.546 2.365 0.079 / 8 m X 76.546 2.365 0.079 / 8
В результате определен доверительный интервал, в котором с доверительной
вероятностью 0,95 располагается истинное значение результата титрования:
76.31 см mX 76.79 см
3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
3
82.
82 Тема 02: Построение эмпирических статистических моделей ХТПII.3.2.1.Процедура исключения незначимых коэффициентов
регрессии
Незначимые коэффициенты следует исключать из уравнения регрессии. Однако
так как матрица C в общем случае недиагональная, и коэффициенты
статически зависимы, то после исключения одного коэффициента необходимо
пересчитать оставшиеся и рассчитать сумму квадратов остаточной дисперсии.
Если она не ухудшилась (не стала больше), то исключение было правомочным. В
противном случае исключение было неправомочным.
В случае незначимости нескольких коэффициентов всегда исключается только
один (т.к. существует статистическая зависимость коэффициентов), причём тот,
для которого отношение
aˆ j
Se C jj
является наименьшим.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
83.
83 Тема 02: Построение эмпирических статистических моделей ХТПОстальные коэффициенты пересчитываются, и, как указывалось выше,
определяется SS R .
Исключение незначимых коэффициентов по одному производится до тех пор,
пока остаточная сумма квадратов не ухудшается.
В случае незначимости нескольких коэффициентов в активном эксперименте изза диагональности матрицы C можно одновременно исключать все
незначимые коэффициенты.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
84.
84 Тема 02: Построение эмпирических статистических моделей ХТПII.3. Проверка адекватности уравнения регрессии - математической
модели. (Выполнение третьего этапа регрессионного анализа).
В результате успешного решения задачи идентификации (параметрической и
структурной) должна получиться адекватная математическая модель (ММ).
Под адекватностью ММ понимается:
1. Качественное и количественное соответствие поведения ММ и объекта
моделирования.
2. Выполнение этого соответствия как при одном наборе режимных параметров
(адекватность состояния), так и при различных наборах режимных
параметров (адекватность поведения).
3. Возможность интерполяции и экстраполяции свойств реального объекта с
помощью ММ.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
85.
85 Тема 02: Построение эмпирических статистических моделей ХТПII.3.1. Оценка адекватности уравнения регрессии
Отношение дисперсии адекватности к дисперсии воспроизводимости
2
расч
ad
2
e
F
S
S
используется для статистической оценки адекватности уравнения регрессии. Для
этой цели применяются таблицы F – распределения Фишера при доверительной
вероятности β (0,9; 0,95; 0,99) и двух числах степеней свободы – дисперсии
адекватности ( f ad ) и дисперсии воспроизводимости ( f e ).
При использовании статистического распределения Фишера всегда
2
рассматривается отношение большей дисперсии (в данном случае - S ad ) к
2
меньшей (в данном случае - Se ).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
86.
86 Тема 02: Построение эмпирических статистических моделей ХТПF-распеделение Фишера при р = 0,05
v2 f e
v1 f ad
ν1 \ ν2
1
2
3
4
5
6
7
8
9
10
1
161,45
199,50
215,71
224,58
230,16
233,99
236,77
238,88
240,54
241,88
2
18,513
19,000
19,164
19,247
19,296
19,330
19,353
19,371
19,385
19,396
3
10,128
9,5521
9,2766
9,1172
9,0135
8,9406
8,8868
8,8452
8,8123
8,7855
4
7,7086
6,9443
6,5914
6,3883
6,2560
6,1631
6,0942
6,0410
5,9988
5,9644
5
6,6079
5,7861
5,4095
5,1922
5,0503
4,9503
4,8759
4,8183
4,7725
4,7351
6
5,9874
5,1433
4,7571
4,5337
4,3874
4,2839
4,2066
4,1468
4,0990
4,0600
7
5,5914
4,7374
4,3468
4,1203
3,9715
3,8660
3,7870
3,7257
3,6767
3,6365
8
5,3177
4,4590
4,0662
3,8378
3,6875
3,5806
3,5005
3,4381
3,3881
3,3472
9
5,1174
4,2565
3,8626
3,6331
3,4817
3,3738
3,2927
3,2296
3,1789
3,1373
10
4,9646
4,1028
3,7083
3,4780
3,3258
3,2172
3,1355
3,0717
3,0204
2,9782
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
87.
87 Тема 02: Построение эмпирических статистических моделей ХТПЭто отношение равно F и для адекватной модели её рассчитанное значение
должно быть не больше стандартного (табличного) значения распределения
Фишера:
F
расч
F
табл
f ad , f e
В противном случае модель считается неадекватной.
Если нет параллельных опытов, то либо сравнивают для моделей остаточные
дисперсии
2
n
ñð.
i
i
2
i 1
R
S
yˆ
y
n p
либо сравнивают эту величину с оценкой разброса опытных данных
относительно среднего значения
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
88.
88 Тема 02: Построение эмпирических статистических моделей ХТПy
ср.
- дисперсией среднего:
S
y
n
2
ср.
n
i 1
i 1
э
i
y
э
y
i
n
2
ср.
n 1
SS ср.
f ср.
2
Так как последняя дисперсия больше S R , то для критерия Фишера
рассматривают отношение Sс2р. к S R2 и условие адекватности будет иметь
вид:
S
2
ср
2
R
S
РХТУ им. Д.И. Менделеева
F
табл
f ср. , f R
Кафедра информатики и компьютерного проектирования
89.
89 Тема 02: Построение эмпирических статистических моделей ХТПIII. Построение эмпирических моделей по данным активного
эксперимента
При проведении опытных исследований различают пассивный и активный
эксперимент.
Методология пассивного экспериментирования предполагает проведение
большой серии опытных исследований с поочередным варьированием значений
входных переменных x и анализом результатов измерений выходной
переменной y (лабораторный эксперимент или эксперимент на пилотной
установке).
К пассивному эксперименту принято относить также и сбор опытных данных в
режиме эксплуатации промышленной установки – т.н. промышленный
эксперимент.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
90.
90 Тема 02: Построение эмпирических статистических моделей ХТПОбработка результатов пассивного эксперимента проводится методами
регрессионного и корреляционного анализа, и выбор вида эмпирической модели
(уравнения регрессии), т.е. решение задачи структурной идентификации
является достаточно сложной задачей.
Это связано с тем, что вид уравнения регрессии необходимо определять по
характеру изменения переменных на графике эмпирической линии регрессии,
полученной по выборке экспериментальных данных.
Для решения этой задачи для одной входной переменной x предложены
эффективные методы, в которых предусматривается преобразование системы
координат как для входной x , так и для выходной переменной y .
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
91.
91 Тема 02: Построение эмпирических статистических моделей ХТППри большем числе входных переменных ( x1 ,...xm ) надёжных методов
определения вида уравнения регрессии (вида эмпирической модели) в
настоящее время не существует.
Активный эксперимент проводится по заранее составленному плану, в
соответствии с которым ставится задача не только определения оптимальных
условий проведения эксперимента, но и оптимизации процесса (оптимальное
планирование эксперимента).
При этом уравнения регрессии (эмпирические модели) описывают данные
активного эксперимента, в основном, в двух ограниченных областях и имеют
следующий вид:
- вдали от экстремального значения выходной переменной y :
m
m 1 m
j 1
j 1 u 2
yˆ a0 a j x j a ju x j xu , u j
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
92.
92 Тема 02: Построение эмпирических статистических моделей ХТП- вблизи экстремального значения выходной переменной y («в почти
стационарной области»):
m
m 1 m
m
j 1
j 1 u 2
j 1
ˆy II a0 a j x j a ju x j xu a jj x 2j (u j )
Приведённые уравнения являются линейными относительно коэффициентов
регрессии a и имеют достаточно простой вид.
Они включают слагаемые с двойным взаимодействием входных переменных
m 1 m
a
j 1 u 2
РХТУ им. Д.И. Менделеева
ju
x j xu
(u j )
Кафедра информатики и компьютерного проектирования
93.
93 Тема 02: Построение эмпирических статистических моделей ХТПи не учитывают взаимодействия более высоких порядков (тройные, четверные и
т.д.), вероятность которых существенно меньше.
Последнее уравнение включает слагаемые с квадратами входных переменных
m
a x
j 1
j
2
j
и его коэффициенты получаются при обработке результатов активных
экспериментов II-го порядка (верхний индекс II при ŷ : ŷ ) – например,
ОЦКП – ортогонального центрального композиционного плана эксперимента.
Предпоследнее уравнение не включает слагаемые с квадратами входных
переменных и его коэффициенты получаются при обработке результатов
активных экспериментов I-го порядка – верхний индекс I при ŷ : ŷ - например,
ПФЭ – полный факторный эксперимент.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
94.
94 Тема 02: Построение эмпирических статистических моделей ХТППри определении оптимальных условий проведения процесса с использованием
эмпирических моделей (например, методом Бокса-Вильсона) выходная
переменная ŷ является критерием оптимальности или целевой функцией.
В теории активного экспериментирования выходную (зависимую) переменную
принято называть функцией отклика, а входные (независимые) переменные –
факторами. Соответственно - координатное пространство с координатами
- факторным пространством, а геометрическое изображение функции отклика в
факторном пространстве – поверхностью отклика.
Активный эксперимент планируется таким образом, чтобы упростить обработку
его результатов методами регрессионного и корреляционного анализа.
Ортогональные планы экспериментов, используемые при активном
экспериментировании, обеспечивают диагональный вид корреляционной
матрицы C при регрессионном анализе и, соответственно, статистическую
независимость коэффициентов регрессии.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
95.
95 Тема 02: Построение эмпирических статистических моделей ХТПК другим достоинствам активного экспериментирования относятся:
- возможность предсказания количества опытов, которые следуют провести;
- определение точек факторного пространства, где следует проводить опыты;
- отсутствие проблем, связанных с выбором вида уравнения регрессии;
- сокращение объёма опытных исследований;
- простота обработки результатов эксперимента методами регрессионного и
корреляционного анализа
- возможность определения оптимальных параметров процесса
экспериментально-статистическим методом;
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
96.
96 Тема 02: Построение эмпирических статистических моделей ХТППФЭ и обработка его результатов
Полный факторный эксперимент (ПФЭ) относится к экспериментам I-го порядка,
т.к. описывающее его уравнение ŷ не включает факторы в квадрате.
Для двух факторов и без учёта взаимодействия факторов соответствующая
эмпирическая модель может быть записана:
yˆ a0 a1 x1 a2 x2
В соответствии с теорией ПФЭ при проведении опытных исследований каждый
из факторов варьируется только на двух уровнях – минимальном (кодированное
значение -1) и максимальном (кодированное значение +1).
При этом реализуются возможные комбинации минимальных и максимальных
значений факторов, в результате чего общее число опытов (n) в ПФЭ равно 2 m и
полный факторный эксперимент обычно называется ПФЭ типа
2.m
Для определения числа опытов применяется формула:
n 2
РХТУ им. Д.И. Менделеева
m
Кафедра информатики и компьютерного проектирования
97.
97 Тема 02: Построение эмпирических статистических моделей ХТПВ последнее уравнение включаются кодированные значения факторов z j
вместо x j , значения которых получаются по следующей схеме кодирования:
0
zj
xj xj
x j
max
x j0 0.5 x min
x
j
j
( j 1, ..., m)
( j 1, ..., m)
min
x j 0.5( x max
x
( j 1, ..., m)
j
j )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
98.
98 Тема 02: Построение эмпирических статистических моделей ХТПВ результате план проведения эксперимента (таблица экспериментов) с учётом
вышесказанного и кодирования факторов имеет вид (m = 2, число опытов n =2m=
4).
z0
z1
z2
y
1
1
1
1
y1
2
1
1
1
y 2
3
1
1
1
y3
1
y 4
p
n
4
1
РХТУ им. Д.И. Менделеева
1
Кафедра информатики и компьютерного проектирования
99.
99 Тема 02: Построение эмпирических статистических моделей ХТППри этом уравнение регрессии, описывающее эти опытные данные,
записывается с использованием кодированных факторов z j ( j 0,1,2) и,
~ , a~ , a~ :
соответственно, кодированных коэффициентов регрессии a
0
1
2
yˆ a~0 a~1 z1 a~2 z 2
В кодированном факторном пространстве в соответствии с указанным планом
проведения эксперимента проведённые опыты представляются точками вершин
квадрата:
2
z
( 1; 1)
( 1; 1)
z1
( 1; 1)
РХТУ им. Д.И. Менделеева
( 1; 1)
Кафедра информатики и компьютерного проектирования
100.
100 Тема 02: Построение эмпирических статистических моделей ХТПДля параметрической идентификации кодированного уравнения регрессии
используется метод регрессионного анализа, включающий три этапа:
~
- определение кодированных коэффициентов уравнения регрессии a
методом наименьших квадратов;
- оценка значимости кодированных коэффициентов регрессии с использованием
t – критерия Стьюдента;
- проверка адекватности кодированного уравнения регрессии с использованием
F – критерия Фишера.
Реализация двух последних этапов возможна при выполнении свойства
однородности дисперсий (одно из требований регрессионного анализа) и
проведении параллельных опытов, например, в центре плана
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
101.
101 Тема 02: Построение эмпирических статистических моделей ХТППри проведении k параллельных опытов в центре плана ( y0эксп
s , s 1, ..., k ) среднее
эксп
значение yc определяется как среднее арифметическое результатов
измерений во всех параллельных опытах:
y
эксп
c
k
y
S 1
эксп
0S
k
Определение кодированных коэффициентов регрессии
В этом случае используется применяемая при линейном регрессионном анализе
матричная формула метода наименьших квадратов (МНК), которая с учётом
кодирования факторов имеет вид:
~
~
a
m 1 n
m 1 1
РХТУ им. Д.И. Менделеева
T
~
n m 1
1
Кафедра информатики и компьютерного проектирования
~
m 1 n
T
y
n 1
эксп
102.
102 Тема 02: Построение эмпирических статистических моделей ХТПгде кодированная матрица, зависящая от независимых переменных для двух
факторов включает только +1 и -1 и имеет вид:
z10
z
~
20
Z
4 3
z30
z40
z11
z21
z31
z41
z12 1
z22 1
z32 1
z42 1
1 1
1 1
1 1
1 1
Матрица z при активном экспериментировании называется матрицей
планирования (часть таблицы экспериментов без столбца вектора
наблюдений y ) и обладает тремя оптимальными свойствами:
- симметричности: сумма элементов всех столбцов матрицы, кроме первого
(точнее, нулевого) равна нулю
n
z
i 1
РХТУ им. Д.И. Менделеева
ij
0 ( j 1, ..., m);
Кафедра информатики и компьютерного проектирования
103.
103 Тема 02: Построение эмпирических статистических моделей ХТП- ортогональности: скалярное произведение двух любых столбцов матрицы
равно нулю
n
T
j u
ij iu
i 1
z z z z 0 ( j, u 0, 1,..., m u j );
- нормировки: скалярное произведение двух одинаковых столбцов матрицы
m
равно n ( n 2 в ПФЭ)
n
z z j z n ( j 0, 1, ..., m).
T
j
i 1
2
ij
Благодаря перечисленным оптимальным свойствам матрицы планирования
информационная матрица в ПФЭ при m=2 равна
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
104.
104 Тема 02: Построение эмпирических статистических моделей ХТПn
0
0
T
T
~
~ ~
Z Z 0 n 0 ,
3 3 3 4 4 3 3 4 4 3
0 0 n
т.е. она является диагональной с одинаковыми элементами на главной
диагонали, равными n = 22 = 4.
Соответственно, корреляционная матрица C также будет диагональной и с
одинаковыми элементами главной диагонали:
1
n
1
1
T
T
~ ~ ~
C Z Z 0
3 3
0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
0
n
1
0
0
0
1
n
105.
105 Тема 02: Построение эмпирических статистических моделей ХТПРезультатом подстановки последних соотношений в матричную формулу для
определения кодированных коэффициентов регрессии будет простая формула:
n
эксп
~
a j zij yi
n,
j 0, 1, ..., m
i 1
При учёте взаимодействия двух факторов z1 и z 2 кодированное уравнение
регрессии принимает вид:
ˆy a~0 z0 a~1 z1 a~2 z2 a~12 z1 z2
и в матрицу планирования z включается ещё один дополнительный последний
столбец, каждый элемент которого равен произведению элементов столбцов,
соответствующих взаимодействующим факторам:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
106.
106 Тема 02: Построение эмпирических статистических моделей ХТПz10
z
~
20
Z
4 4
z30
z 40
z11
z12
z 21
z 22
z31
z32
z 41
z 42
z11 z12 1
z 21 z 22 1
z31 z32 1
z 41 z 42 1
1 1 1
1 1 1
1 1 1
1 1 1
При этом матрица планирования сохраняет все три оптимальных свойства –
симметричности, ортогональности и нормировки, а кодированный коэффициент
уравнения регрессии при члене, характеризующем взаимодействие факторов,
определяется по формуле:
эксп
~
a ju zij ziu yi
n,
n
j, u 1, ..., m u j
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
107.
107 Тема 02: Построение эмпирических статистических моделей ХТПВ теории ПФЭ доказывается, что при увеличении числа факторов (m>2) матрица
z строится с использованием рассмотренной методики, в том
планирования
числе и с учётом взаимодействия факторов (не только двойного, но и тройного,
четверного и т.д.).
В этом случае число столбцов матрицы p зависит от числа учёта взаимодействий
(n=планирования
2m )
факторов
и матрица
сохраняет перечисленные
оптимальные свойства.
Поэтому для определения кодированных коэффициентов регрессии
используются приведённые выше формулы.
Для расчёта натуральных значений коэффициентов в кодированное уравнение
регрессии вместо кодированных факторов z j j 1,...m следует подставить
выражения для последних через натуральные значения факторов x j j 1,...m
в соответствии с приведённой выше схемой кодирования.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
108.
108 Тема 02: Построение эмпирических статистических моделей ХТПОпределение значимости кодированных коэффициентов регрессии
Незначимость кодированных коэффициентов регрессии определяется с
использованием квантиля t – распределения Стьюдента t т абл
f e при помощи
неравенства:
a~ j
S a~ j
t
табл
fe
где β – доверительная вероятность (в инженерных расчётах равная 0,95);
fe – число степеней свободы дисперсии воспроизводимости (при одной серии
параллельных опытов равная k -1).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
109.
109 Тема 02: Построение эмпирических статистических моделей ХТПВыборочное значение квадратного корня дисперсии кодированного
коэффициента регрессии определяется по формуле:
~
Sa~ j C jj Se ,
где S e - квадратный корень из дисперсии воспроизводимости, определяемой
по k параллельным опытам в центре плана эксперимента:
y
k
S
2
e
j 1
2
эксп
0j
y
эксп
c
k 1
SSe
fe
SSe - сумма квадратов дисперсии воспроизводимости;
f e - число степеней свободы дисперсии воспроизводимости.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
110.
110 Тема 02: Построение эмпирических статистических моделей ХТПКак было показано выше, диагональные элементы корреляционной матрицы в
ПФЭ при кодировании факторов одинаковы и равны 1/n, вследствие чего
Se
S a~ j
n
В результате условие незначимости кодированных коэффициентов регрессии
принимает вид:
~
aj
Se
n t
табл
fe
~
Так как корреляционная матрица C в этом случае является диагональной, то
кодированные коэффициенты регрессии статистически независимы и при
одновременной незначимости нескольких кодированных коэффициентов
регрессии они (в отличие от процедуры обработки пассивного эксперимента)
могут быть сразу, все вместе, исключены из кодированного уравнения регрессии.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
111.
111 Тема 02: Построение эмпирических статистических моделей ХТППроверка адекватности уравнения регрессии
Проводится так же, как и при проведении пассивного эксперимента, с
использованием табличного значения критерия Фишера, выбранного при
доверительной вероятности β (чаще всего равной 0,95) и числе степеней
свободы остаточной дисперсии ( f R ) и дисперсии воспроизводимости ( f e ) .
F
расч
F
табл
f ad , f e
где
F
РХТУ им. Д.И. Менделеева
расч
2
ad
2
e
S
S
Кафедра информатики и компьютерного проектирования
112.
112 Тема 02: Построение эмпирических статистических моделей ХТПК недостаткам ПФЭ относится резкое увеличение числа опытов при
возрастании количества факторов больше, чем 5 ( при m = 5 n = 25 = 32 ).
Для проведения регрессионного анализа при пренебрежении целым рядом
несущественных взаимодействий факторов достаточно проводить меньшее
число опытов. В этом случае можно реализовать часть ПФЭ, т.н. дробный
факторный эксперимент (ДФЭ), который здесь не рассматривается.
К достоинствам ПФЭ относится свойство ротатабельности получаемого при его
обработке линейного уравнения регрессии первого порядка:
m
yˆ a~0 z0 a~j z j
j 1
где
0
zj
РХТУ им. Д.И. Менделеева
xj xj
x j
Кафедра информатики и компьютерного проектирования
113.
113 Тема 02: Построение эмпирических статистических моделей ХТПСвойство ротатабельности
Свойство ротатабельности характеризует равную предсказательную способность
уравнения регрессии с кодированными факторами на одинаковом расстоянии от
центра плана эксперимента
Предсказательная способность оценивается оценкой дисперсии yˆ S yˆ ,
~
которая из-за статистической независимости коэффициентов a j и одинаковой
дисперсии коэффициентов Sa2 Se2 n ( j 0, 1, ..., m) определяется по
j
формуле:
2
m
S y2ˆ S a~20 z 2j S a~2j S a~2 (1 2 )
j 1
где 2 - квадрат расстояния от центра плана эксперимента до конкретной точки
факторного пространства:
m
z 2j
2
j 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
114.
114 Тема 02: Построение эмпирических статистических моделей ХТППрименение уравнения первого порядка
Для определения направления проекции градиента в факторном пространстве
при поиске максимума целевой функции ŷ или проекции антиградиента в
случае поиска минимума этой функции.
Вектор градиента определяет направление наискорейшего возрастания функции
и равен:
yˆ
yˆ
yˆ
grad yˆ
i
j ...
m
x1
x2
xm
где i , j , m - единичные векторы в направлении осей координат
yˆ
(i 1, ..., m ) - проекции вектора градиента на оси координат x1 , x2 , ..., xm
xi
определяемые из конкретного вида уравнения 1-го
порядка с известными коэффициентами â
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
115.
115 Тема 02: Построение эмпирических статистических моделей ХТПОпределение проекций градиента в факторном пространстве
Последовательные координаты поиска экстремума в факторном пространстве
определяется по формуле:
xi s 1 xi( s ) h ( s )
yˆ ( s )
xi
yˆ ( s ) 2
(
)
j 1 x j
m
(i 1, ..., m; s 0, 1, ..., m)
где i – номер координаты градиента; s – номер точки экспериментирования;
h(s) – задаваемый фактор шага в точке экспериментирования s
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
116.
116 Тема 02: Построение эмпирических статистических моделей ХТПГрафическое изображение движения к экстремуму функции двух
переменных градиентным методом
x 0 , x 1 - центры планов эксперимента первого порядка (ПФЭ);
x 2 - центр плана эксперимента второго порядка (ОЦКП)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
117.
117 Тема 02: Построение эмпирических статистических моделей ХТПУсловие близости проекции оптимума в факторном пространстве
Область в окрестности проекции оптимума называется «почти стационарной
областью»
Условие близости точки оптимума функции ŷ может быть установлено с
помощью t – критерия Стьюдента путем оценки значимости различия между
экспериментальными и расчетными величинами в центре плана ПФЭ (zj = 0, j = 1,
…, m)
ycэ* a~0
Se
где
k
y yiэ k
э*
c
i 1
и
t
та б л
( fe )
yˆ 0 a~0
При выполнении этого критерия в «почти стационарной области» необходимо
проводить эксперимент ОЦКП
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
118.
118 Тема 02: Построение эмпирических статистических моделей ХТПОЦКП и обработка его результатов
Ортогональный центральный композиционный эксперимент (ОЦКП) относится к
экспериментам II – го порядка, так как описывающее его уравнение ŷ
включает факторы в квадрате и поэтому может описывать поверхности функций
отклика в окрестности их экстремальных значений.
Для двух факторов ( x1 и x2 ) с учётом только двойного взаимодействия
факторов соответствующая эмпирическая модель может быть записана:
yˆ a0 a1 x1 a2 x2 a12 x1 x2 a x a x
II
2
11 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
2
22 2
119.
119 Тема 02: Построение эмпирических статистических моделей ХТПВ соответствии с методикой ортогонального центрального композиционного
плана эксперимента (ОЦКП) здесь, также как и для ПФЭ, осуществляется
кодирование факторов по приведённой выше схеме, и для обеспечения
ортогонального свойства матрицы планирования эксперимента в уравнение
регрессии ŷ включается некоторая постоянная S.
В результате уравнение регрессии при m = 2 принимает вид:
2
2
~
~
~
~
~
~
yˆ a0 z0 a1 z1 a2 z2 a12 z1 z2 a11 z1 S a22 z2 S
Для определения большего числа кодированных коэффициентов, чем при
обработке ПФЭ, и описания поверхности функции отклика вблизи её экстремума
(«почти стационарной области»), количество опытов в этом случае
увеличивается.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
120.
120 Тема 02: Построение эмпирических статистических моделей ХТППри этом опыты, проводимые при ПФЭ (n 2 m ) , дополняются опытами в
«звёздных» точках факторного пространства (n 2m) и опытами в центре
плана (nc ) с координатами z1 0 и z2 0
«Звёздные» точки в факторном пространстве располагаются на осях координат
на расстоянии +α и –α от центра плана эксперимента; причём величина α
называется «звёздным» плечом и её значения, так же как величина S,
определяются из условия ортогональности матрицы планирования z для ОЦКП.
Общее число опытов N в ортогональном центральном композиционном
эксперименте определяется по формуле:
N n n nc ,
или с учётом приведённых выше равенств:
N 2 2m nc .
m
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
121.
121 Тема 02: Построение эмпирических статистических моделей ХТПДля случая двух факторов (m = 2):
N 8 nc
Расположение опытных точек в факторном пространстве для случая двух
факторов в приведённой ранее кодированной системе координат может быть
представлено:
z2
( 1; 1)
( 1; 1)
(0;0)
( 1; 1)
РХТУ им. Д.И. Менделеева
( 1; 1)
Кафедра информатики и компьютерного проектирования
z1
122.
122 Тема 02: Построение эмпирических статистических моделей ХТППлан проведения экспериментов (таблица эксперимента) в этом случае может
быть представлен:
p
n
2m
2m
nc
z12 S z 22 S
y
z0
z1
z2
1
+1
-1
-1
+1
1-S
1-S
y1
2
+1
+1
-1
-1
1-S
1-S
y 2
3
+1
-1
+1
-1
1-S
1-S
y3
4
+1
+1
+1
+1
1-S
1-S
y 4
5
+1
-α
0
0
α2-S
-S
y5
6
+1
+α
0
0
α2-S
-S
y6
7
+1
0
-α
0
-S
α2-S
y7
8
+1
0
+α
0
-S
α2-S
y8
9
+1
0
0
0
-S
-S
y9
+1
0
0
0
-S
-S
N
+1
0
0
0
-S
-S
y N
z1 z 2
Матрица планирования z представляет собой часть плана проведения
эксперимента без горизонтальных и вертикальных заголовков таблицы и вектора
наблюдения y (правого столбца).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
123.
123 Тема 02: Построение эмпирических статистических моделей ХТПОпределение величины «звёздного плеча» α и S из условия
ортогональности матрицы планирования
Матрица планирования Z
следующие равенства:
была бы ортогональной, если бы выполнялись
z z j S 0 ( j 1, 2)
T
0
2
и
z
2
1
S
z
T
2
2
S 0
Раскрывая первое равенство, можно получить:
N
N
z z j S z z zi 0 S n 2α NS 0
T
0
2
i 1
РХТУ им. Д.И. Менделеева
2
i 0 ij
2
i 1
Кафедра информатики и компьютерного проектирования
j 1, 2
124.
124 Тема 02: Построение эмпирических статистических моделей ХТПОткуда:
n 2α
S
N
2
Раскрывая второе равенство, получаем:
z
2
1
S
z
T
2
2
n n 2α 2
z z S S z S S
S S n 2α NS n 2 NS NS
2 T
1
S z
2 T
1
2
2
2
2
n NS 2 0
Откуда:
S
n
N
Последнее выражение используется для определения S.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
T
2
2
T
2
2
125.
125 Тема 02: Построение эмпирических статистических моделей ХТППриравнивая правые части двух выражений для S, можно найти формулу для
определения α :
2
n 2
N
1
2
2
n
N
n N
Nn n
1
2 n
В результате звёздное плечо α можно определить по формуле:
n N
1
2 n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
126.
126 Тема 02: Построение эмпирических статистических моделей ХТПОпределение кодированных коэффициентов регрессии (1-й этап)
В соответствии с методом наименьших квадратов эти коэффициенты
определяются по матричной формуле:
T
~
~
a C z y ,
~
C z z
T
где
1
Из-за свойства ортогональности матрицы планирования z необходимо
определить только диагональные элементы информационной матрицы:
T
~
z z,
а затем диагональные элементы корреляционной матрицы:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
~ ~
C
1
127.
127 Тема 02: Построение эмпирических статистических моделей ХТПОпределение диагональных элементов информационной и
корреляционной матриц
Обобщая уравнение регрессии на случай m факторов и учитывая только все
двойные взаимодействия факторов, число которых определяется по формуле:
m m 1
C
,
2!
2
m
общее число коэффициентов уравнения регрессии для m факторов равно:
m(m 1)
p 1 m
m,
2!
~
диагональные элементы информационной матрицы определяются:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
128.
128 Тема 02: Построение эмпирических статистических моделей ХТП~
число этих элементов равно 1
I 00 N
~
2
I jj n 2 j 1,...m ;
m m 1
~
I ju n u j число этих элементов равно:
2!
~
Для определения при квадратах факторов I jj можно записать:
2
~
2
2
2
I jj = n(1− S) +2(α − S) + (N− n− 2)S =
¿n− 2nS+nS2 +2α 4− 4α 2 S+2 S2+NS2− nS2− 2S2=
2
4
¿2α 4 +n− 2S(⏟
n+2α2 )+NS2= 2α4 +n−
NS
=
2α
⏟
NS
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
0
129.
129 Тема 02: Построение эмпирических статистических моделей ХТПКоличество таких диагональных элементов – m.
Диагональная матрица имеет размер:
m m 1
m 1 m 2
p 1 m
m
2
2
что соответствует числу определяемых параметров p.
~ ~ 1 размером р х р
В результате диагональная корреляционная матрица C
для m факторов и с учётом их двойных взаимодействий имеет вид:
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
130.
130 Тема 02: Построение эмпирических статистических моделей ХТПN 1
C
p p
n 2α
2 1
n 2α
2 1
n 1
n 1
2α
4 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
4 1
2α
1
m
m m 1
2
m
131.
131 Тема 02: Построение эмпирических статистических моделей ХТПЭлементы корреляционной матрицы определяются по матричной формуле МНК:
~ T эксп
~
a CZ y
Кодированные коэффициенты регрессии определяются:
N
a~0
y
i 1
N
эксп
i
N
z z y
N
a~ ju
i 1
a~ j
ij iu
z
i 1
ij
y
эксп
i
n 2α
z
N
эксп
i
n
РХТУ им. Д.И. Менделеева
, u j
a~jj
i 1
( j 1, ..., m)
2
2
ij
Кафедра информатики и компьютерного проектирования
S yiэксп
2α
4
( j 1, ..., m)
132.
132 Тема 02: Построение эмпирических статистических моделей ХТПДля пересчёта этих коэффициентов регрессии в натуральные значения
необходимо вместо кодированных факторов z подставить их натуральные
величины x j в соответствии с приведённой схемой кодирования.
Определение значимости кодированных коэффициентов регрессии
(2-й этап)
В отличие от ПФЭ значимость коэффициентов регрессии определяется по
разным формулам для различных коэффициентов, так как диагональные
элементы корреляционной матрицы C~ отличаются друг от друга.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
133.
133 Тема 02: Построение эмпирических статистических моделей ХТПС учётом общей формулы для определения незначимости коэффициентов
регрессии
~
aj
табл
t
fe
~
C jj S e
незначимость каждого вида коэффициента регрессии определяется:
~
a0
Se
~
a
j
Se
РХТУ им. Д.И. Менделеева
N t
табл
fe
;
n 2 t
2
табл
fe
( j 1,...m)
Кафедра информатики и компьютерного проектирования
134.
134 Тема 02: Построение эмпирических статистических моделей ХТПa~ ju
Se
n t
табл
fe
~
a jj
Se
число коэффициентов
2 t
4
табл
fe
m m 1
;
2
( j 1,...m)
Проверка адекватности уравнения регрессии (3-й этап)
Осуществляется с использованием критерия Фишера – так же, как и в случае с
ПФЭ.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
135.
135 Тема 02: Построение эмпирических статистических моделей ХТППрименение уравнения второго порядка
Уравнение регрессии с m факторами второго порядка вида:
m
m 1 m
m
j 1
j 1 u 2
j 1
yˆ a~0 a~ j z j a~ ju z j zu a~ jj z 2j S
(u j )
может применяться для определения экстремума функции отклика с
использованием необходимого условия экстремума функции многих
переменных:
yˆ
0
z1
yˆ
0
z m
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
136.
136 Тема 02: Построение эмпирических статистических моделей ХТППолученная система линейных уравнений (СЛАУ) позволяет расчётным путём
( j 1,... m) и после подстановки их величин в исходное
определить z opt
j
уравнение ŷ получить максимальное или минимальное значение функции
отклика.
opt
Координаты экстремума ŷ - z j ( j 1,... m) определены корректно, если для
них выполняется следующие условия:
1 z opt
j 1
( j 1,...m)
Справедливость этого условия обусловлена тем, что используется кодированное
уравнение регрессии второго порядка с максимальными значениями факторов
+1 и минимальными значениями факторов -1.
При невыполнении этих условий для проведения эксперимента ОЦКП
opt
используется новый центр плана, соответствующий полученным значениям z
Процедура оптимизации экспериментально-статистическим методом БоксаВильсона приведена на следующем слайде и сводится к последовательным
сериям сначала экспериментов 1-го порядка (ПФЭ) и затем серии экспериментов
II-го порядка (ОЦКП).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
137.
137 Тема 02: Построение эмпирических статистических моделей ХТП~
xicor xi 0 h
~
a
i
m
a~
j 1
2
j
i 1,...m
Ввод
x 0 x cor
Старт
x cor
zj
x
x j x j0
x j
Обработка
результатов
ПФЭ
ПФЭ
j 1,...m
x 0 x cor
zj
x j x j0
x j
j 1,...m
ОЦКП
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
Оптиму
м
близок
138.
138 Тема 02: Построение эмпирических статистических моделей ХТПОЦКП
x cor
x j0 z opt
j
j x j
Обработка результатов ОЦКП
j 1,...m
Решение системы
yˆ II
0
z j
z opt
1
j
j 1,...m
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Вывод
z opt
j
j 1,...m
Стоп
j 1,...m
139.
139 Тема 02: Построение эмпирических статистических моделей ХТПРХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
140.
140 Тема 02: Построение эмпирических статистических моделей ХТПЗадания для самопроверки
1. В чем заключается линеаризация MM относительно коэффициентов? Почему
использование линейных и линеаризованных моделей упрощает процедуру
определения их коэффициентов?
2. Какие экспериментальные данные необходимы для решения задачи
идентификации? Зачем нужны стартовые, уточняющие и дискриминирующие
эксперименты?
3. Как определяются коэффициенты ММ методом интерполяции и методом
аппроксимации? Какой из этих методов является более предпочтительным?
4. В чем состоит сущность метода наименьших квадратов (МНК)?
5. Внимательно проанализируйте алгоритм вычисления коэффициентов ММ этим
методом. Почему в случае линейных моделей вместо решения задачи
оптимизации используют необходимое условие экстремума функции критерия
МНК и решают систему уравнений?
6. Как определяется значимость коэффициентов линейных моделей? Почему
процедура исключения незначимых коэффициентов является различной, когда
обрабатываются результаты пассивного и активного (например, полного
факторного - ПФЭ) эксперимента?
7. Как проверяется адекватность математических моделей?
В чем заключается адекватность состояния и адекватность поведения?
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного моделирования
141.
141 Тема 02: Построение эмпирических статистических моделей ХТП7. Как установить пригодность математической модели для интерполяции и
экстраполяции свойств реального объекта?
8. Напишите системы уравнений, которые необходимо решить для вычисления
коэффициентов уравнения Аррениуса методом интерполяции и методом
аппроксимации.
9. Как определяются коэффициенты уравнения Антуана методом наименьших
квадратов? Запишите систему уравнений, решаемую для определения
коэффициентов линеаризованной модели.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
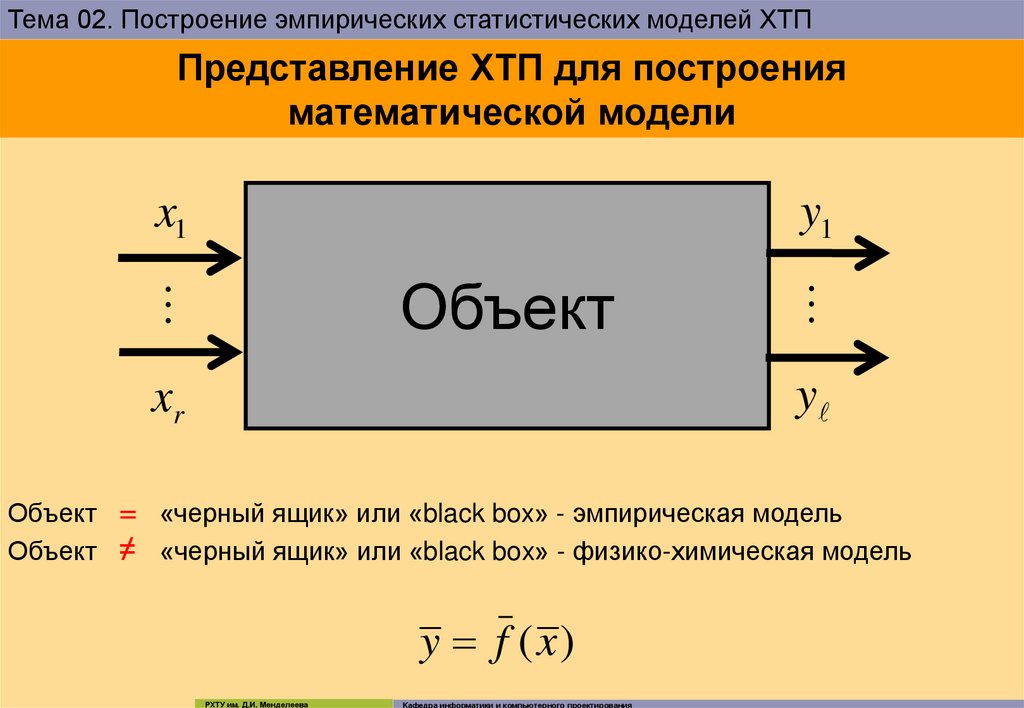

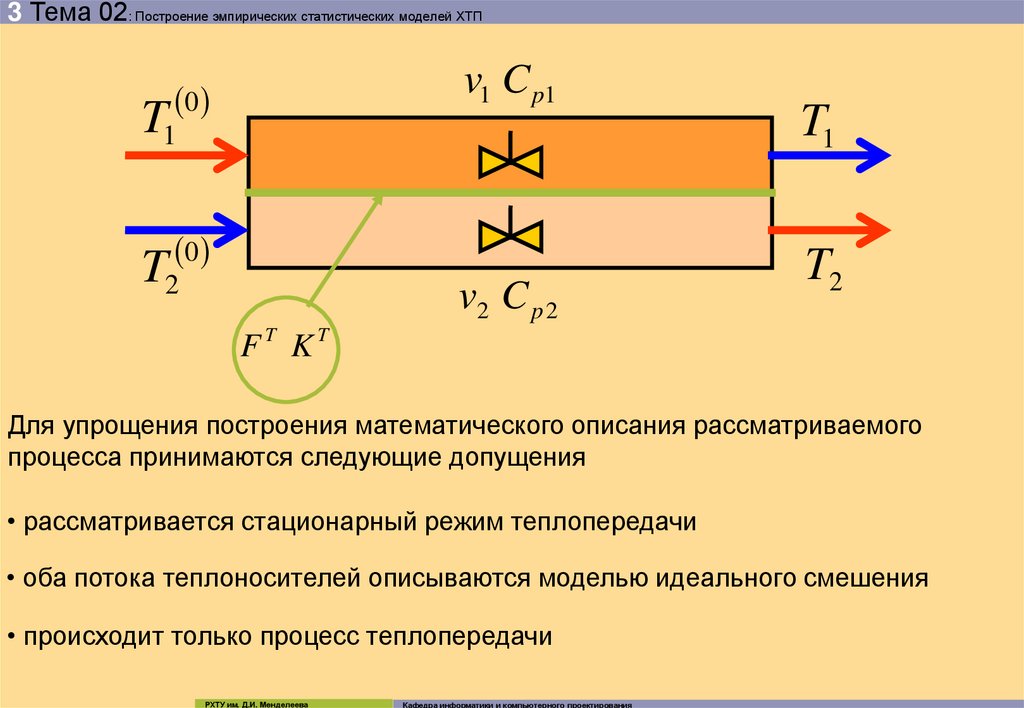
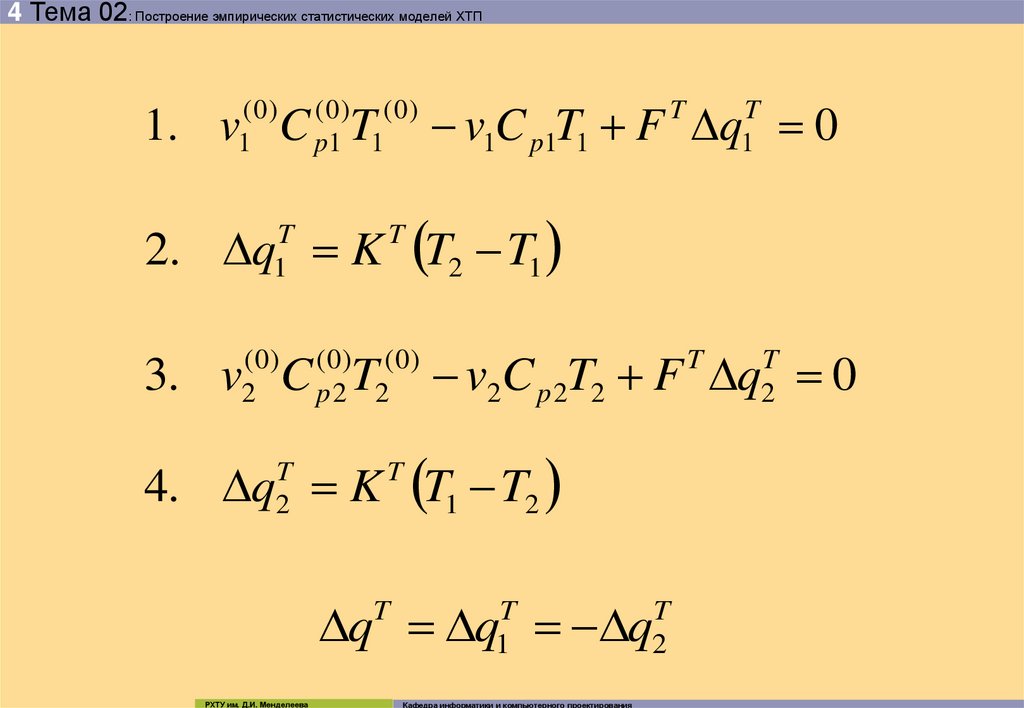








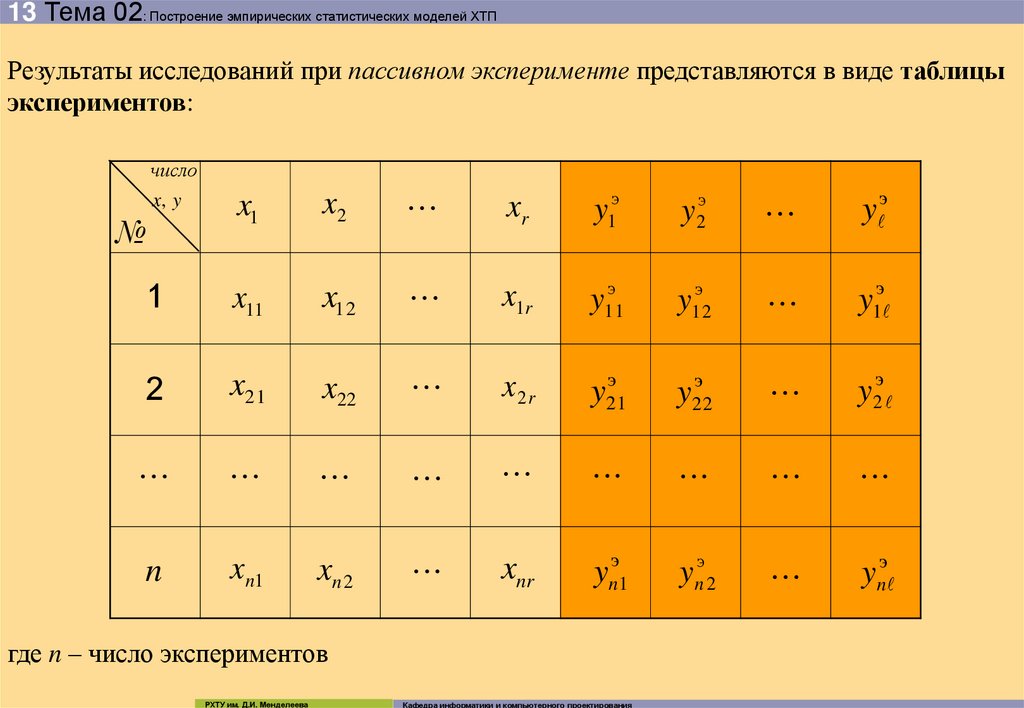


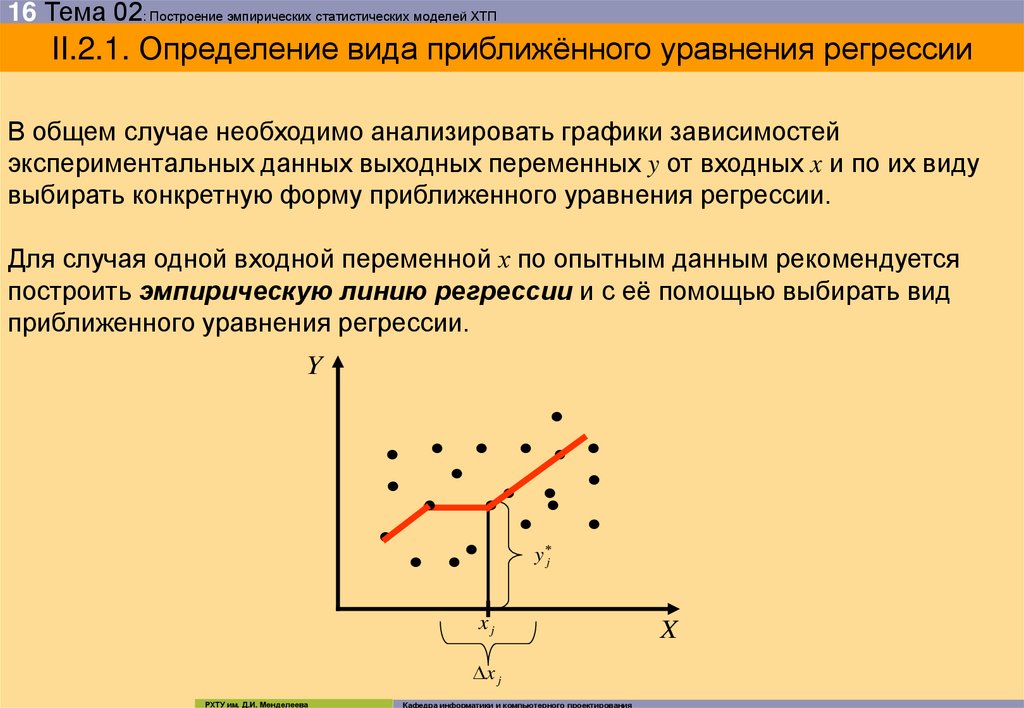









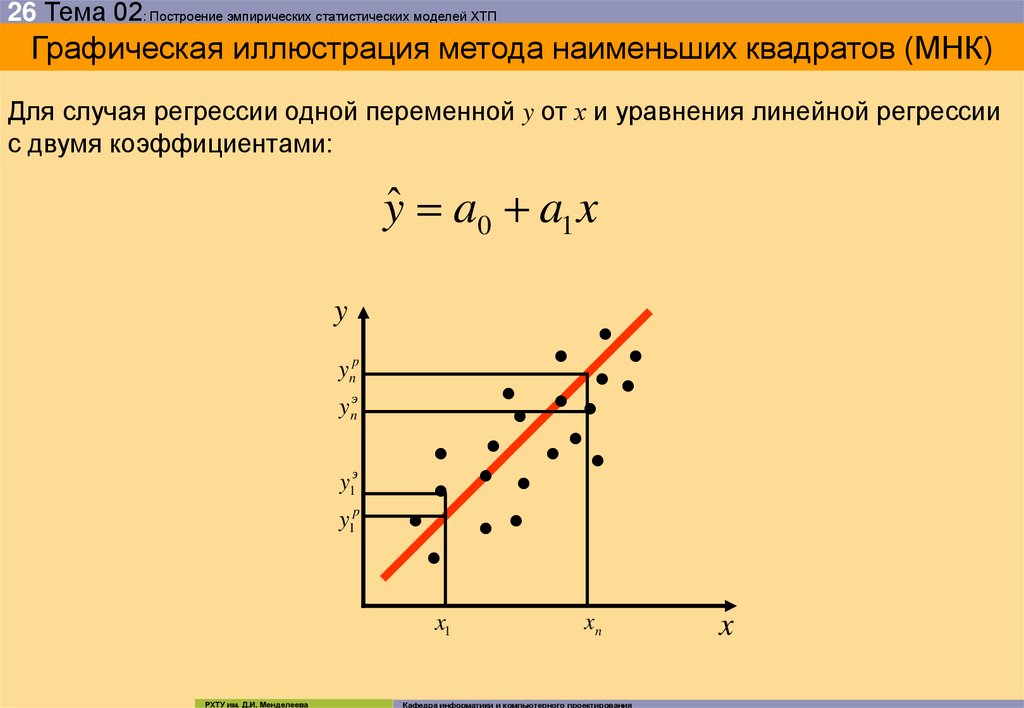




















































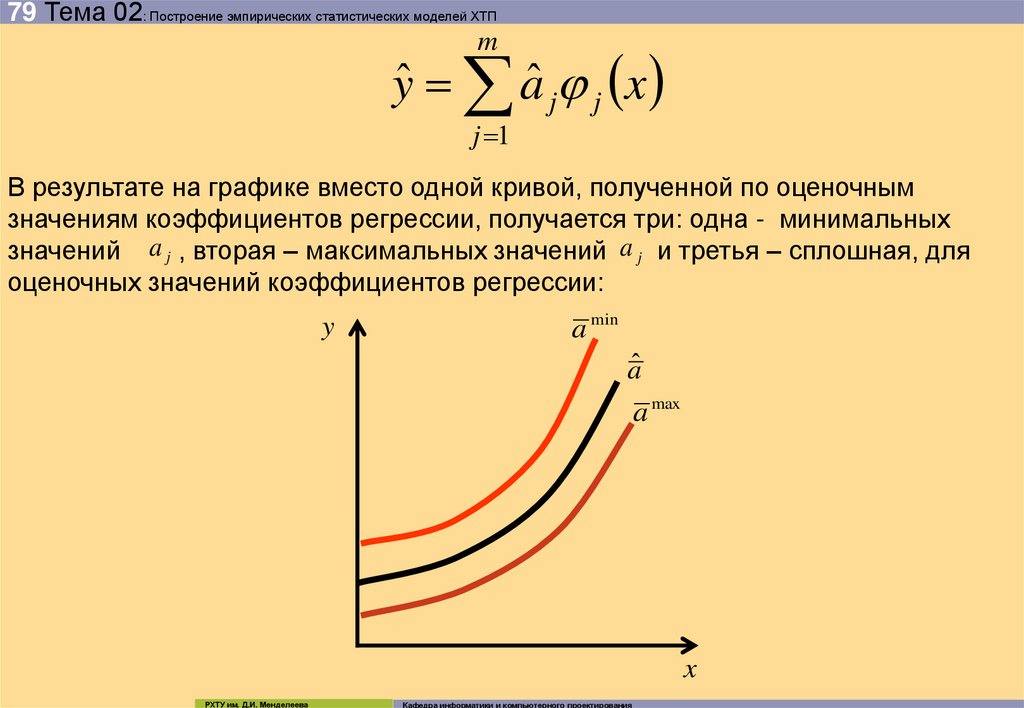






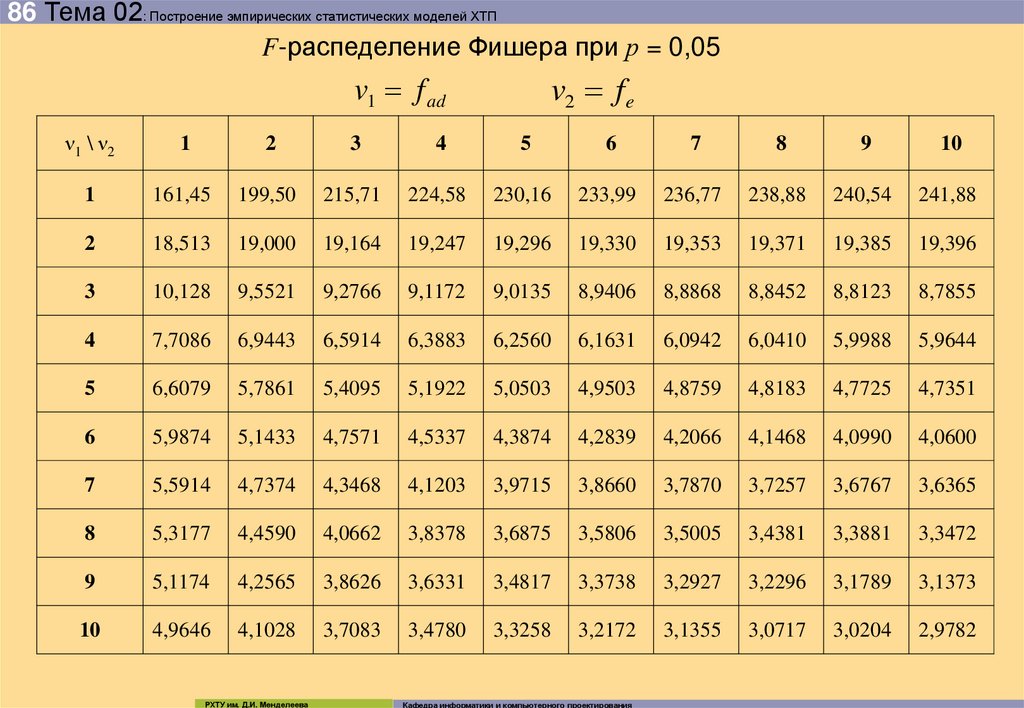





























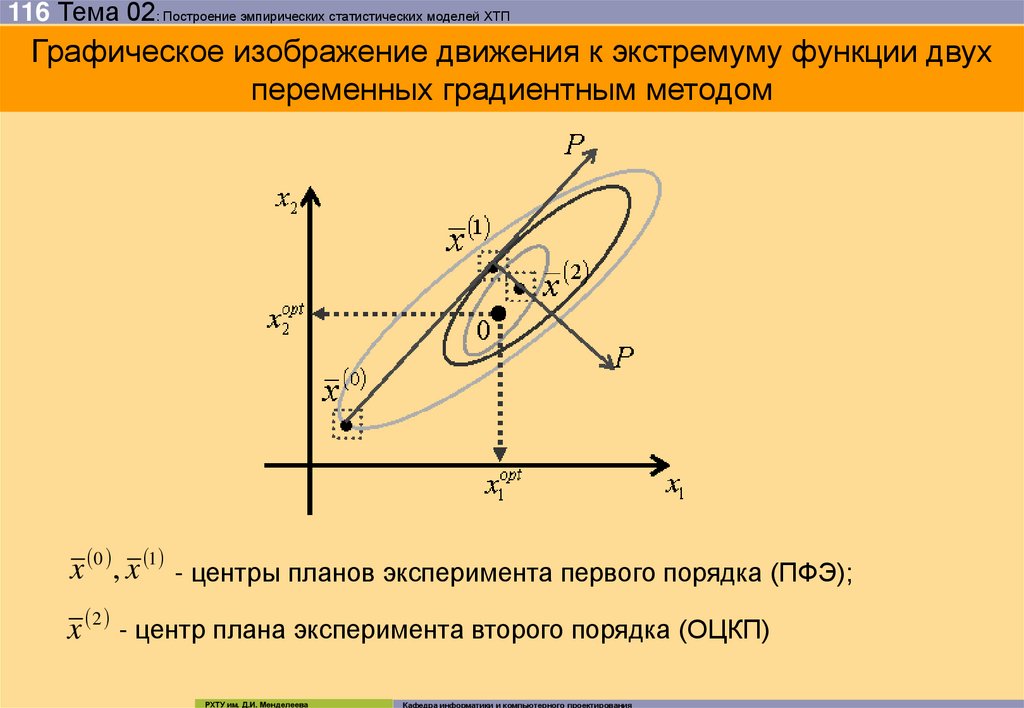




















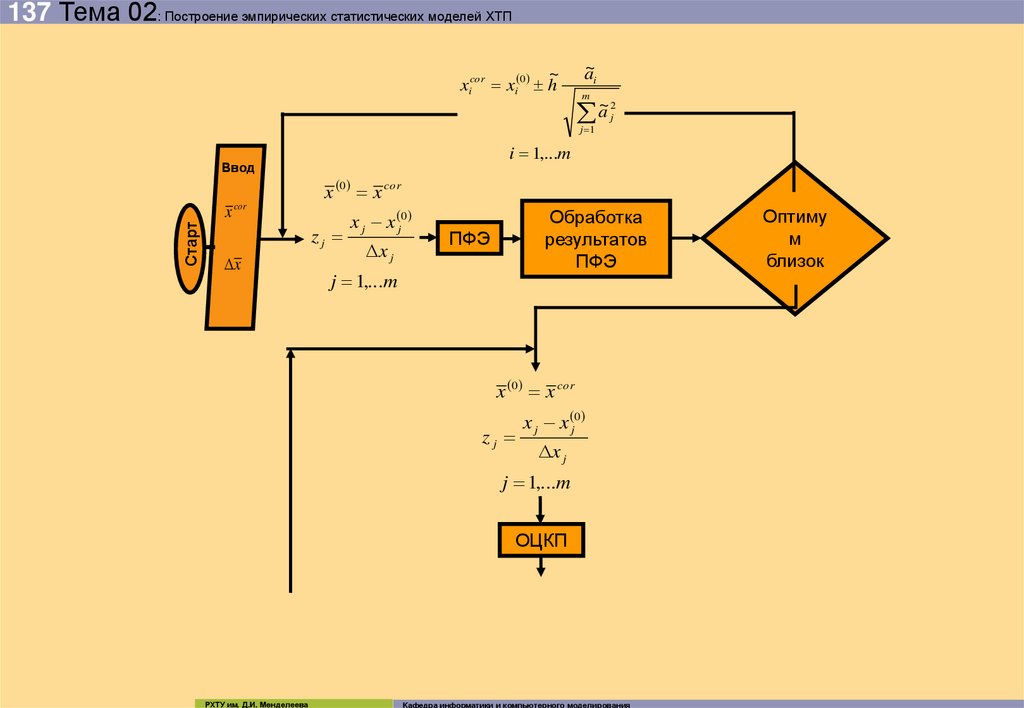
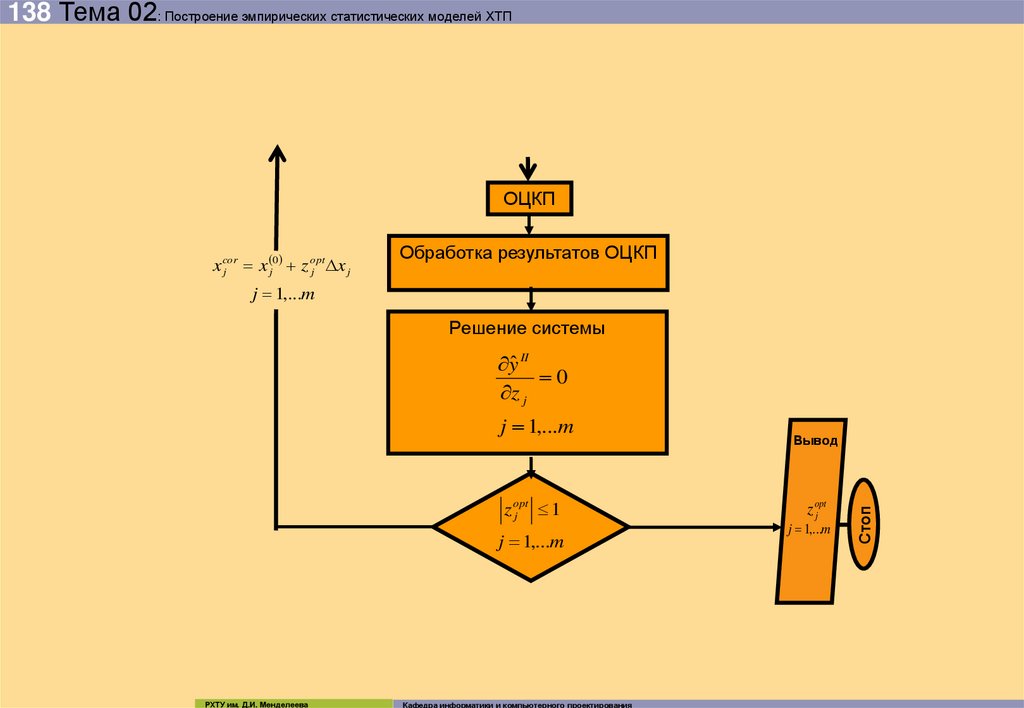



 mathematics
mathematics chemistry
chemistry








