Similar presentations:
Моделирование химико-технологических процессов
1.
Кафедра информатики и компьютерногопроектирования
Моделирование химико-технологических
процессов
Лекторы:
1. Советин Филипп Сергеевич, кандидат технических наук,
доцент;
2. Шумакова Ольга Петровна, кандидат технических наук,
доцент;
3. Новикова Дина Константиновна, кандидат химических наук,
доцент;
4. Царёва Елена Владимировна, кандидат технических наук,
доцент.
1
2.
Лекция № 8Построение теоретических физико-химических моделей
химико-технологических процессов
2
3.
Представление ХТП для построенияматематических моделей
y1
x1
Объект
y
xr
Объект = «черный ящик» или «black box» - эмпирическая модель
Объект ≠ «черный ящик» или «black box» - физико-химическая модель
y f (x )
3
4.
Принципы построения теоретических физикохимических моделейПоследовательные этапы
• Изучается теория процесса
• Составляется система уравнения математического описания (МО)
• Выбирается алгоритм решения системы уравнений МО, т.н.
моделирующий алгоритм (МА)
• МА реализуется на компьютере и получается математическая модель
(ММ)
• Проверяется адекватность модели путем сравнения расчетных
результатов с экспериментальными
• В случае отсутствия адекватности модели решается задача
идентификации
4
5.
При построении теоретической физико-химическоймодели ХТП на основании знания механизмов
протекающих процессов:
•Составляется система уравнений математического описания (МО)
•Разрабатывается или выбирается алгоритм решения системы
уравнений математического описания, т.н. моделирующий алгоритм
(МА)
•Моделирующий алгоритм решения уравнений математического
описания реализуется на компьютере в виде расчетного модуля
технологического процесса в конкретном аппарате
В результате получается математическая модель ХТП, реализованная на
компьютере, которая в случае ее адекватности используется для исследования
реального производства.
5
6.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕОРЕТИЧЕСКИХ ФИЗИКО-ХИМИЧЕСКИХМОДЕЛЕЙ ХТП
Химико-технологические процессы обычно протекают в движущихся потоках фаз,
гидродинамические закономерности перемещения которых оказывают влияние
на эффективность химических производств.
Выбор конструкций аппаратов химической технологии во многом связан с
необходимостью обеспечения требуемых гидродинамических условий
проведения процессов.
Поэтому основу уравнений МО ХТП составляют балансовые уравнения для
потоков вещества (массы), теплоты (энтальпии) и импульса (количества
движения), записанные с учётом гидродинамических закономерностей их
движения.
Применяются так называемые комбинированные гидродинамические модели
движения потоков. Они представляют собой комбинации описаний зон аппаратов
с более простыми гидродинамическими моделями движения потоков, в
частности, комбинации моделей идеального смешения, идеального вытеснения
6
и однопараметрической диффузионной модели.
7.
Основная особенность простых моделей состоит в том, что они содержатминимальное число параметров:
• модель идеального смешения – объём;
• модель идеального вытеснения – объём и длину;
• однопараметрическая диффузионная модель – объём, длину и коэффициент
продольного перемешивания.
7
8.
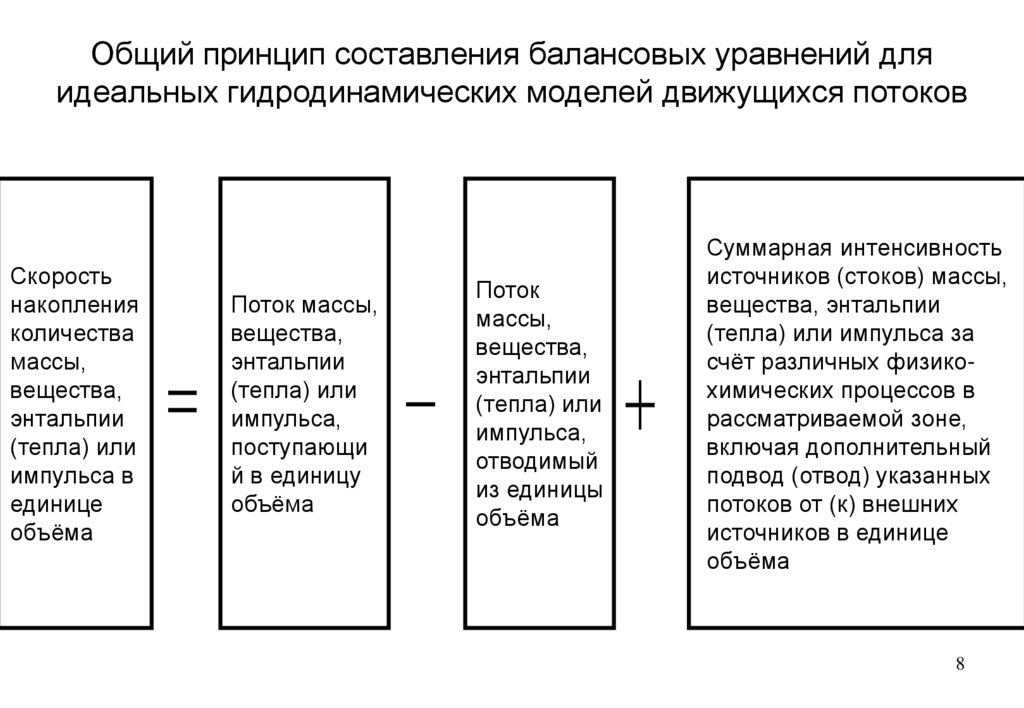
Общий принцип составления балансовых уравнений дляидеальных гидродинамических моделей движущихся потоков
Скорость
накопления
количества
массы,
вещества,
энтальпии
(тепла) или
импульса в
единице
объёма
Поток массы,
вещества,
энтальпии
(тепла) или
импульса,
поступающи
й в единицу
объёма
Поток
массы,
вещества,
энтальпии
(тепла) или
импульса,
отводимый
из единицы
объёма
Суммарная интенсивность
источников (стоков) массы,
вещества, энтальпии
(тепла) или импульса за
счёт различных физикохимических процессов в
рассматриваемой зоне,
включая дополнительный
подвод (отвод) указанных
потоков от (к) внешних
источников в единице
объёма
8
9.
В общем случае балансовые уравнения гидродинамики записывают отдельнодля
• массы;
• веществ (компонентов) многокомпонентной смеси;
• теплоты (энтальпии);
• импульса
и распространяют на всю движущуюся систему с учётом её полного объёма и
длины
Поток массы - это общая масса многокомпонентной смеси, протекающая в
единицу времени в рассматриваемой системе.
Поток вещества (компонента) является частным случаем потока массы. Термин
относится только к массе выбранного i-го компонента.
Поток теплоты или энтальпии - это поступающее (отводимое) в единицу
времени в (от) систему (системы) количество теплоты (энтальпии), отнесённое к
стандартному состоянию.
Поток импульса (количества движения) характеризуется значением подводимого
(отводимого) в единицу времени к (от) системе импульса. Используется редко.
9
10.
1011.
1112.
1213.
1314.
1415.
Математическое описание зоны потока, движение фазы в которойпредставляется гидродинамической моделью идеального
смешения
Объекты, описываемые моделью идеального смешения, относятся к объектам с
сосредоточенными параметрами.
x 0 , T 0
x, T
15
16.
Динамическая модель1 n ) Уравнения покомпонентных балансов
R
(0) (0)
i
i
dV x
v
dt
x
vxi G , i 1,..., n
Σ
i
2) Уравнение общего баланса массы
R
n
dV
(0)
v v Gi
dt
i 1
3) Уравнение теплового баланса
R
d V C PT
(0) (0) (0)
v C P T vC P T Q
dt
16
17.
Система (n + 2) обыкновенных дифференциальных уравнений (СОДУ)используется для математического описания нестационарных режимов
процессов с сосредоточенными параметрами.
В систему уравнений дополнительно должны быть включены выражения для
определения интенсивностей источников всех компонентов
G (i 1, ..., n)
Σ
i
и теплоты
Q
Результатом решения системы уравнений должны стать функции, отражающие
зависимость от времени концентрации компонентов xi, реакционного объёма VR
и температуры потока Т:
x
x t
V
R*
*
i
V
R*
*
i
t
(i 1, ..., n)
T T t
*
*
17
18.
Статическая модель1 n ) Уравнения покомпонентных балансов
( 0)
( 0)
i
v x
vxi G 0 i 1, ..., n
Σ
i
2) Уравнение общего баланса массы
n
v
( 0)
v G 0
i 1
i
3) Уравнение теплового баланса
(0)
(0)
P
v C T
(0)
vCP T Q 0
18
19.
Система (n + 2) конечных уравнений (СКУ) используется для описаниястационарных режимов процессов с сосредоточенными параметрами.
В эту систему уравнений также должны быть включены выражения для
определения интенсивностей источников всех компонентов и теплоты
Результатом решения конечной системы уравнений должны стать расчётные
значения концентраций, расхода реакционного потока и температуры:
x ,
v*, T *
19
20.
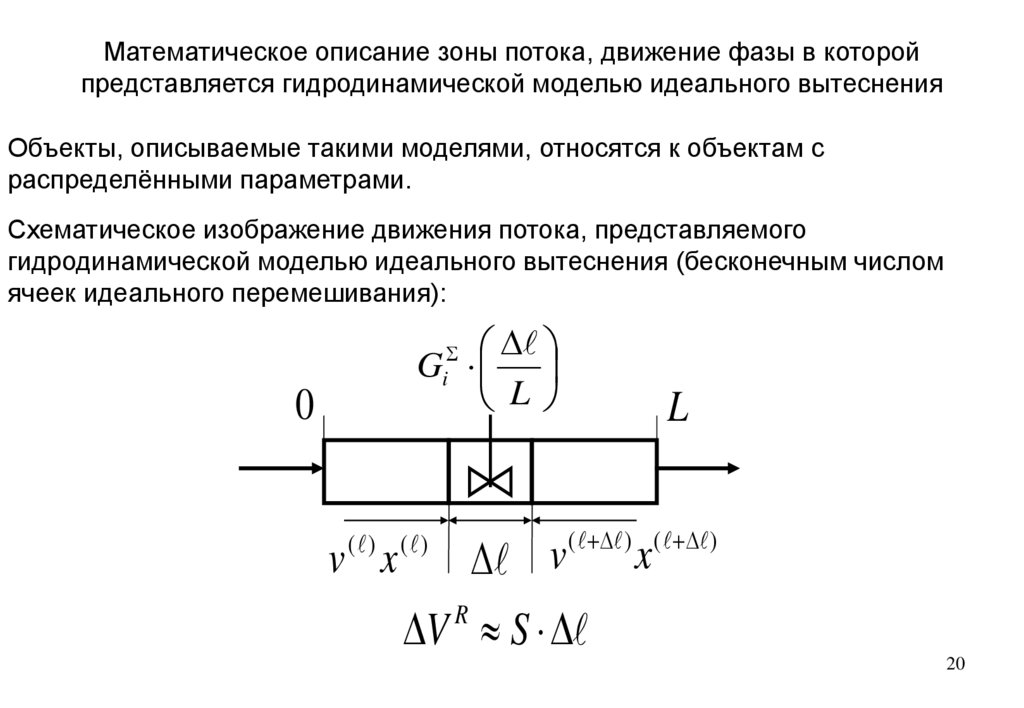
Математическое описание зоны потока, движение фазы в которойпредставляется гидродинамической моделью идеального вытеснения
Объекты, описываемые такими моделями, относятся к объектам с
распределёнными параметрами.
Схематическое изображение движения потока, представляемого
гидродинамической моделью идеального вытеснения (бесконечным числом
ячеек идеального перемешивания):
G
L
i
0
v
( ) ( )
v x
L
( ) ( )
x
V S
R
20
21.
Вывод формулы для динамической моделиЕсли предположить, что в одной ячейке идеального
смешения
R
V S
Уравнения математического описания по аналогии с
приведёнными выше уравнениями
Σ
d S x i
G
( ) ( )
( ) ( )
i
v xi v
xi
dt
L
(i 1, ..., n )
Площадь поперечного сечения при допущении о
цилиндрической форме трубы с постоянным сечением
R
выражается
V
S
L
21
22.
v ( ) xi( ) v ( ) xi( ) G iΣd VR x i
L dt
L
(i 1, ..., n )
При стремлении интервала Δl нулю (Δl →0) получаем уравнения
покомпонентных балансов
22
23.
Динамическая модель1 n ) Уравнения покомпонентных балансов
V xi
vx i
Σ
G i (i 1, ..., n )
L t
где
R
G
Σ
i
Σ
i
G
L
2) Уравнение общего баланса массы
R
1 V
v
Gi
L t
i 1
n
3) Уравнение теплового баланса
R
P
V C T
vC P T
Q
L t
23
24.
Для описания нестационарных режимов процессов с распределённымипараметрами, движение потока фаз в которых представляется
гидродинамической моделью идеального вытеснения (трубчатый аппарат),
используется система дифференциальных уравнений в частных производных
(СДУЧП)
В эту систему уравнений должны быть включены выражения для определения
интенсивностей источников всех компонентов и теплоты
Результатом решения системы уравнений должны стать расчётные значения
концентраций, расхода реакционного потока и температуры в зависимости от
двух независимых координат – времени и длины реактора
x x t, , i 1, ..., n;
*
Vi
*
t, ,
*
T T t, ,
R
V
R*
t
( 0)
t t
0 L;
(k )
;
24
25.
Статическая модель1 n ) Уравнения покомпонентных балансов
d v xi
Σ
Gi
d
(i 1, ..., n)
2) Уравнение общего баланса массы
n
dv
Gi
d i 1
3) Уравнение теплового баланса
d vC P T
Q
d
25
26.
Для описания стационарных режимов процессов с распределённымипараметрами, движение потока в которых представляется гидродинамической
моделью идеального вытеснения, когда изменение переменных происходит
вдоль одной пространственной координаты, используется система
обыкновенных дифференциальных уравнений (СОДУ)
В эту систему уравнений должны быть включены выражения для определения
интенсивностей источников всех компонентов и теплоты
Решением данной системы уравнений математического описания должны стать
зависимости концентрации, расхода реакционной смеси и температуры от
пространственной координаты
x x (i 1, ..., n)
v* v *
T* T *
26
27.
Математическая модель стационарного режима процесса втеплообменниках типа «смешение – вытеснение»
Построение компьютерной модели теплообменника включает следующие этапы:
• изучение и/или ознакомление с теорией процесса теплообмена для данного
типа теплообменных аппаратов
• построение математического описания (МО) конкретного процесса
теплообмена
• выбор и реализация алгоритма (моделирующего алгоритма – МА) решения
уравнений МО модели данного теплообменника
27
28.
Математическая модель стационарного режима процесса втеплообменнике типа «смешение – вытеснение»
Резервуар
v1 C p1
0
T1
0
T2
0
v2 C p 2
T1
L
T2 ( L)
Змеевик
28
29.
Для построения математического описания данной модели примем следующиедопущения:
• поток, проходящий через резервуар, описывается гидродинамической моделью
идеального смешения
• поток в змеевике описывается гидродинамической моделью идеального
вытеснения
• рассматривается стационарный режим работы теплообменника
• коэффициент теплопередачи считается постоянным
• никаких процессов кроме теплопередачи не происходит
• теплоёмкости теплоносителей одинаковы и не меняются с изменением
температуры
29
30.
3031.
3132.
3233.
( 0)1
( 0) ( 0)
p1 1
1. v C T
v1C p1T1 F q 0
T
T
1
2. q1T K T T2 T1
dT2 F T
3. v2 C p 2
q2T
d
L
4. q2T K T T1 T2
С учетом справедливости равенств:
qT q1T q2T
33
34.
выведем уравнение общего теплового баланса:v1 0 C p 01 T1 0 v1 C p1T [ F T q T ]cp 0
Произведение [ F T qT ]ср представляет собой усреднённое по длине змеевика
значение.
Чтобы определить скорость теплопередачи в рассматриваемой модели
теплообменника, необходимо проинтегрировать функцию [ F T qT ]ср по длине
змеевика и разделить на длину змеевика
L
1
[ F q ]cp F T q T d
L0
T
T
L
dT2
[ F q ]cp v 2 C p 2
d v 2 C p 2 T2 L T2 0
d
0
34
T
T
35.
Система уравнений МО рассматриваемой модели теплообменника, такимобразом, будет состоять из следующих уравнений:
• уравнения общего теплового баланса:
0) (0)
1. ⏟
− v2 C p2 [T 2 (L )− T 2 (0)]+v(10) C(p1
T 1 − v1 C p1 T 1= 0
f1
• обыкновенного дифференциального уравнения в явном виде для потока
теплоносителя в змеевике:
dT2
FT
T
2.
q f 2
d Lv2C p 2
• выражения для локальной скорости теплопередачи:
3. q K T2 T1
T
T
35
36.
Для решения дифференциального уравнения 2 (вычисления частного решенияна компьютере), к данной системе уравнений МО необходимо добавить
начальное условие:
0
2 . T2 0 T2
В данном случае дополнительное условие 2’ задаётся при одном значении
независимой переменной, то есть решается задача Коши.
T
T2 0 T2 0
T2 1
T2 2
0
L
L
36
37.
Для решения системы уравнений производную в уравнении 2 целесообразнопредставить в конечно-разностном виде, в результате чего получается система
уравнений с начальным условием для дифференциального уравнения:
0) (0)
1. ⏟
− v2 C p2 [T 2 (L )− T 2 (0)]+v(10) C(p1
T 1 − v1 C p1 T 1= 0
f1
T2 L T2 0
F
2.
qT f 2
Lv2C p 2
T
3. qT K T T2 T1
0
2 . T2 0 T2
37
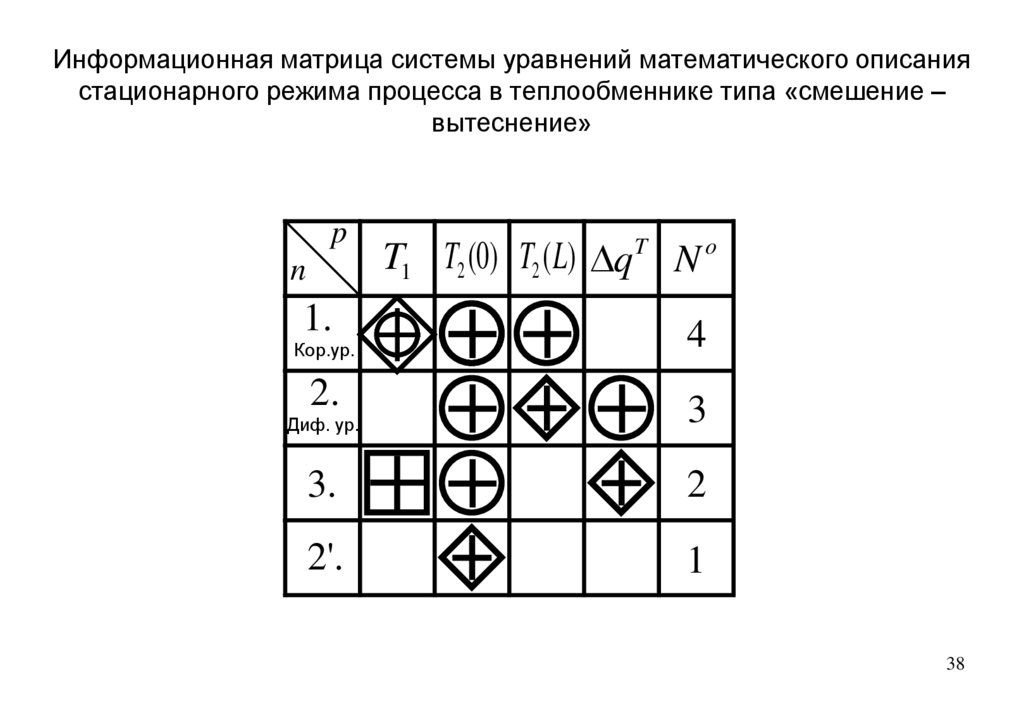
38.
Информационная матрица системы уравнений математического описаниястационарного режима процесса в теплообменнике типа «смешение –
вытеснение»
p
n
1.
Кор.ур.
2.
T1 T2 (0) T2 ( L) q T N o
4
Диф. ур.
3
3.
2
2'.
1
38
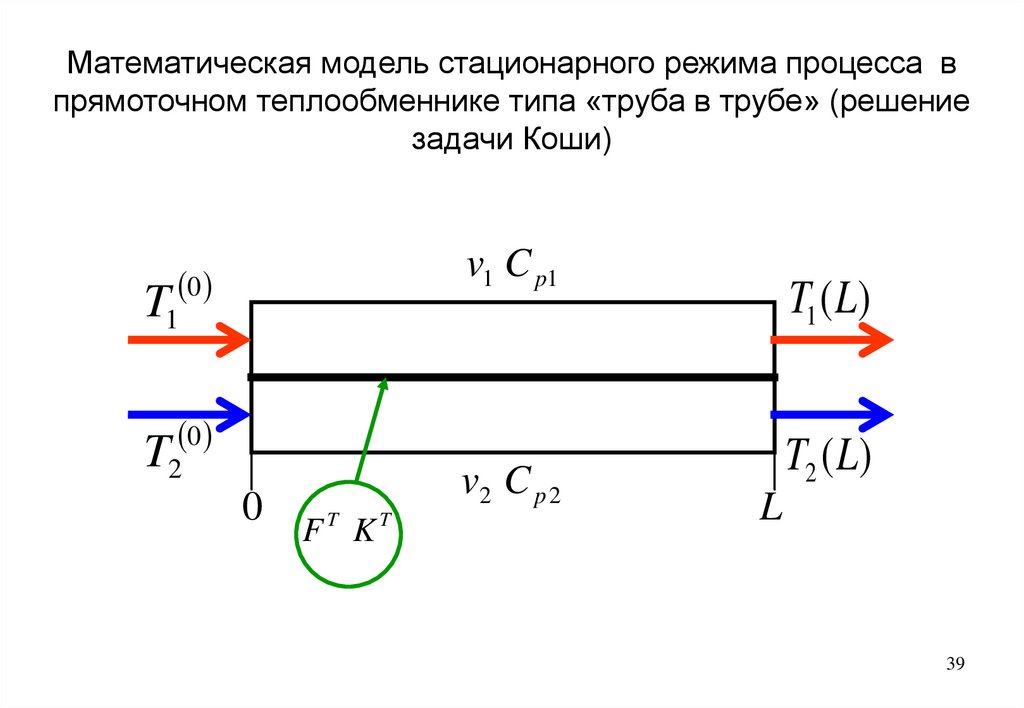
39.
Математическая модель стационарного режима процесса впрямоточном теплообменнике типа «труба в трубе» (решение
задачи Коши)
v1 C p1
0
T1
T1 ( L)
0
T2
0
v2 C p 2
T
F K
T
T2 ( L)
L
39
40.
Для построения системы уравнений математического описания процесса впрямоточном теплообменнике типа «труба в трубе» принимаются следующие
допущения:
• рассматривается стационарный режим процесса теплопередачи
• кроме процесса теплопередачи не происходит никаких других процессов
• коэффициент теплопередачи постоянен и известен (решение прямой задачи)
• теплоёмкость потоков теплоносителей постоянна
• поверхность теплообмена равномерно распределена вдоль участка длины
теплообменника
• движение первого и второго потоков теплоносителей описывается
гидродинамической моделью идеального вытеснения
40
41.
dT1 F T1. v1C p1
q1T
d
L
T
T
2. q1 K T2 T1
3. v2C p 2
dT2 F T
q2T
d
L
4. q K T1 T2
T
2
T
С учетом справедливости равенств:
qT q1T q2T
41
42.
Система уравнений МО модели прямоточного теплообменника типа «труба втрубе» записывается как СОДУ в конечно-разностном представлении с
начальными условиями, заданными при 0 :
T
T
L
T
0
F
1
1 . 1
q T f1
Lv1C p1
T2 L T2 0
F
2.
qT f 2
Lv2C p 2
T
3. q T K T T2 T1
1
2
T1 0 T1 0
0
0
T2 0 T2
42
43.
Поскольку начальные условия задаются при одном и том же значениинезависимой переменной, в данном случае решается задача Коши.
Задание начальных условий и изменение температур теплоносителей по длине
теплообменника типа «труба в трубе»:
T1 , T2
(0)
1
T
1
T1
T1 L
(0)
2
T
2
0
T2
T2 L
L
43
44.
Информационная матрица системы уравнений математического описаниястационарного режима процесса в прямоточном теплообменнике типа «труба в
трубе»
p
n
1
Диф. ур.
T1 0 T1 ( L) T2 0 T2 ( L) q T
No
4
2
Диф. ур.
5
3
3
1'
1
2'
2
44
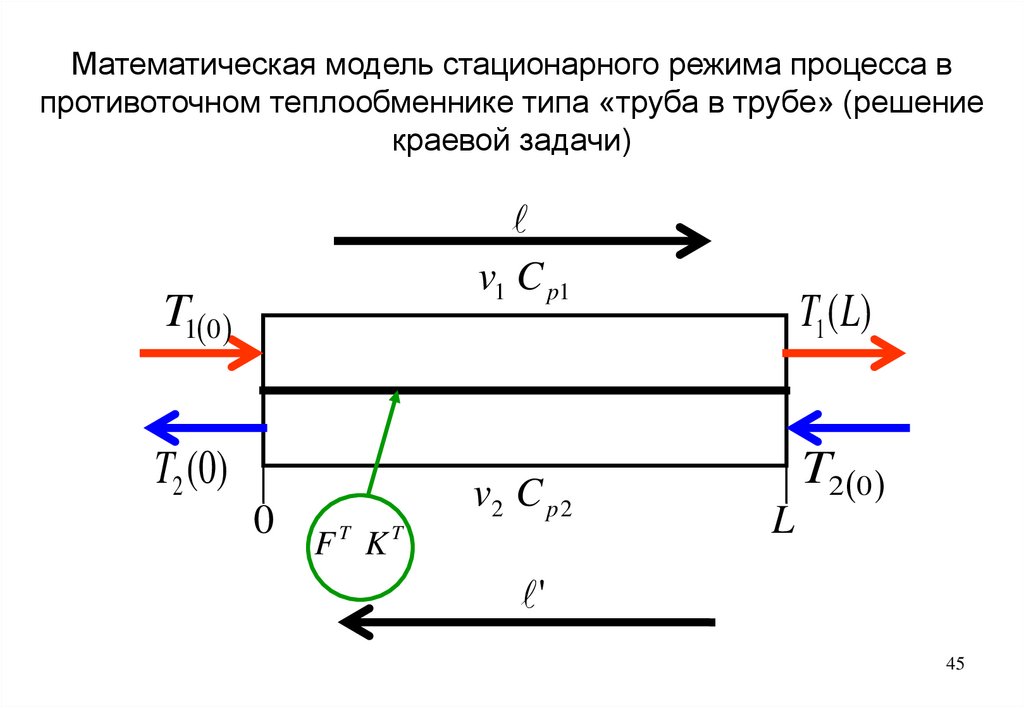
45.
Математическая модель стационарного режима процесса впротивоточном теплообменнике типа «труба в трубе» (решение
краевой задачи)
v1 C p1
T1 0
T2 (0)
0
v2 C p 2
T
F K
T
T1 ( L)
T2 0
L
'
45
46.
dT1FT
1.
q1T
d Lv1C p1
2. q K T2 T1
dT2
FT
T
3.
q
2
'
d
Lv2C p 2
T
1
T
4. q2T K T T1 T2
' L
d ' d
С учетом справедливости равенств:
q q q
T
T
1
T
2
46
47.
Система уравнений МО теплообменника типа «труба в трубе» записывается какСОДУ в конечно-разностном представлении с краевыми условиями, заданными
при разных значениях пространственной координаты
T
T
L
T
0
F
1
1 . 1
q T f1
Lv1C p1
T2 L T2 0
F
2.
qT f 2
Lv2C p 2
T
3. q K T2 T1
T
T
1 . T1 0 T1 0
2 . T2 L T2 0
47
48.
Задача получения частного решения системы обыкновенныхдифференциальных уравнений, если дополнительные условия заданы при
разных значениях пространственной координаты, называется краевой задачей.
Задание краевых условий и изменение температур теплоносителей по длине
теплообменника «труба в трубе» (противоток):
T1 , T2
T1( 0 )
1
T1
T1 ( L)
~
T2 0
T2
0
2
T2 ( 0 )
T2 ( L)
L
48
49.
Процедура решения краевой задачи~
1. Задается приближение для температуры T2 (0) при 0 , отсутствующее в
исходной постановке задачи
2. Решается система двух дифференциальных
уравнений (1) и (2) с учетом
~
дополнительных условий T1 0 и T2 (0) , в результате чего при L
получаются приближенные значения:
~
T1 L T2 (0)
~
T2 L T2 (0)
3. В том случае, когда краевое условие 2’ не превращается в равенство, оно
~
используется для коррекции приближения T2 (0) до тех пор, пока не будет
получено решение получаемого уравнения 2’ следующего вида:
~
T2 L T2 (0) T2( 0) 0
Решение последнего уравнения во внешнем цикле с учетом получаемых
зависимостей T1
и
при финальном значении
T2 (0 L)
~
приближения T2 (0) - T2 (0) означает решение краевой задачи
49
50.
Информационная матрица системы уравнений математического описаниястационарного режима процесса в противоточном теплообменнике типа «труба в
трубе»
p
n
T1 0 T1 ( L) T2 0 T2 ( L) q T
№
1
3
2
Диф. ур.
4
3
2
1
1
2
5
Диф. ур.
Кор.ур.
50
51.
Химические реакторы. Моделированиехимических реакторов
51
52.
Математические модели стационарных и нестационарных режимовхимических реакторов
Микрокинетика сложной химической реакции
Для построения математических моделей процессов в гомогенных химических
реакторах с участием n компонентов в m стадийной химической реакции на
микрокинетическом уровне необходимо решить две задачи:
1. Определить локальную скорость химической реакции по каждому компоненту
– вектор скоростей химической реакции по каждому компоненту
m
R
i
ij j
j 1
g α r
(i 1,..., n)
2. Определить локальную скорость выделения или поглощения теплоты в
химической реакции
m
R
R
pj
pj
j
j 1
q α
H r
52
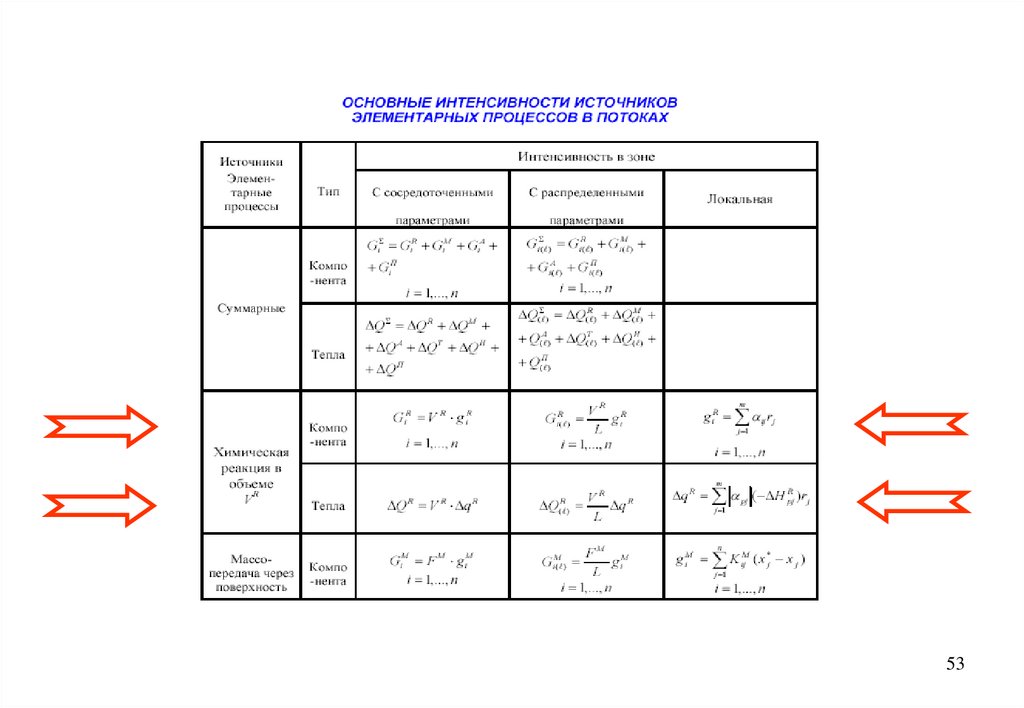
53.
5354.
В матричном виде выражение для скорости химической реакции по компонентузаписывается следующим образом:
g α r
R
g1R α11 α1m r1
g nR α n1 α nm rm
Рассмотрим следующую схему химических превращений:
2A B
k1
k2
2C
k3
D
54
55.
Скорость j–й элементарной стадии химической реакции в жидкой фазеопределяется по закону действующих масс:
n
rj k j x
χ ij
ij
j 1,..., m
i 1
Для рассматриваемого уравнения реакции выражения для скоростей стадий
записываются следующим образом:
r1 k1 x x x x k1 x x B ;
2
A
1
B
0
C
0
D
2
A
r2 k 2 x x x x k 2 x ;
0
A
0
B
2
C
0
D
2
C
r3 k 3 x x x x k x .
0
A
0
B
2
C
0
D
2
3 C
55
56.
gg
g
g
R
A
R
B
R
C
R
D
2 2
0
r1
1
1
0
r2
2 2 2
r3
0
1
0
g 2r1 2r2 ;
R
A
g r1 r2 ;
R
B
g 2r1 2r2 2r3 ;
R
C
g r3 .
R
D
56
57.
Для рассматриваемого уравнения реакции, с учётом приведённых выкладок дляскоростей стадий реакции, выражение для локальной скорости выделения
(поглощения) тепла за счет химической реакции записывается следующим
образом:
q R 2 H CR1 r1 1 H BR2 r2 1 H DR3 r3
Константы скоростей стадий реакции в соответствии с законом Аррениуса
выражаются следующим уравнением:
k j A j exp E j RT ;
j 1, ..., 3
57
58.
Выбор ключевых компонентов химической реакцииКлючевые компоненты – это компоненты, задание которых однозначно
характеризует состояние процесса, сопровождаемого химической реакцией, в
любой момент времени.
Уравнения математического описания с учётом гидродинамических условий и
микрокинетических закономерностей записываются только для ключевых
компонентов, в то время как расчёт остальных (не ключевых) компонентов
производится по стехиометрическим соотношениям.
Число ключевых компонентов химической реакции равно рангу матрицы
стехиометрических коэффициентов.
Рангом матрицы называется максимальный порядок её минора, отличного от
нуля.
58
59.
Матрица стехиометрических коэффициентов для рассматриваемого уравнения:2
0
2
1
1
0
α
2 2 2
0
1
0
Все миноры матриц 3Х3 матрицы стехиометрических коэффициентов равны 0:
2
0
2 2 0
2
2
0
1
1
0
2 2 2
0 0 1
0
0
1
0
0
1
1 1
2
1
0 ; 2 1 1 0 ; 3 2 2 2 ; 4 2 2 2
59
60.
Для матриц 2Х2 есть миноры не равные 0, т.е. наивысший (максимальный)порядок минора матрицы стехиометрических коэффициентов равен 2.
Ранг матрицы стехиометрических коэффициентов равен 2, и число ключевых
компонентов трёхстадийной реакции с четырьмя компонентами А, В, С и D равно
2.
Исходя из микрокинетических соотношений, запишем выражения для скоростей
химической реакции по компонентам:
1 R
g gA
2
R
R
R
gC g A 2g D
R
B
1 R
R
g g A gC
2
R
D
60
61.
Для рассматриваемой реакции в качестве ключевых выбираем компоненты А иС.
Скорости химической реакции по компонентам В и D выражаются через
стехиометрические соотношения следующим образом:
dx B 1 dx A
g
dt
2 dt
R
B
0
xB xB
1
0
xA xA
2
dxD
1 dx A dxC
g
dt
2 dt
dt
R
D
0
xD xD
1
0
0
x A x A xC xC
2
61
62.
Окончательный вид системы уравнений для описания скоростей химическойреакции по компонентам включает два микрокинетических уравнения (вместо
первоначальных четырёх) для двух ключевых компонентов А и С и два
стехиометрических соотношения для определения концентраций компонентов B
иD
1
2
3
4
g AR 2k1 x A2 x B 2k 2 xC2 ;
1
x B x B x A x A0 ;
2
g CR 2k1 x A2 x B 2k 2 xC2 2k 3 xC3 ;
0
0
xD xD
1
x A x A0 xC xC 0 .
2
62














































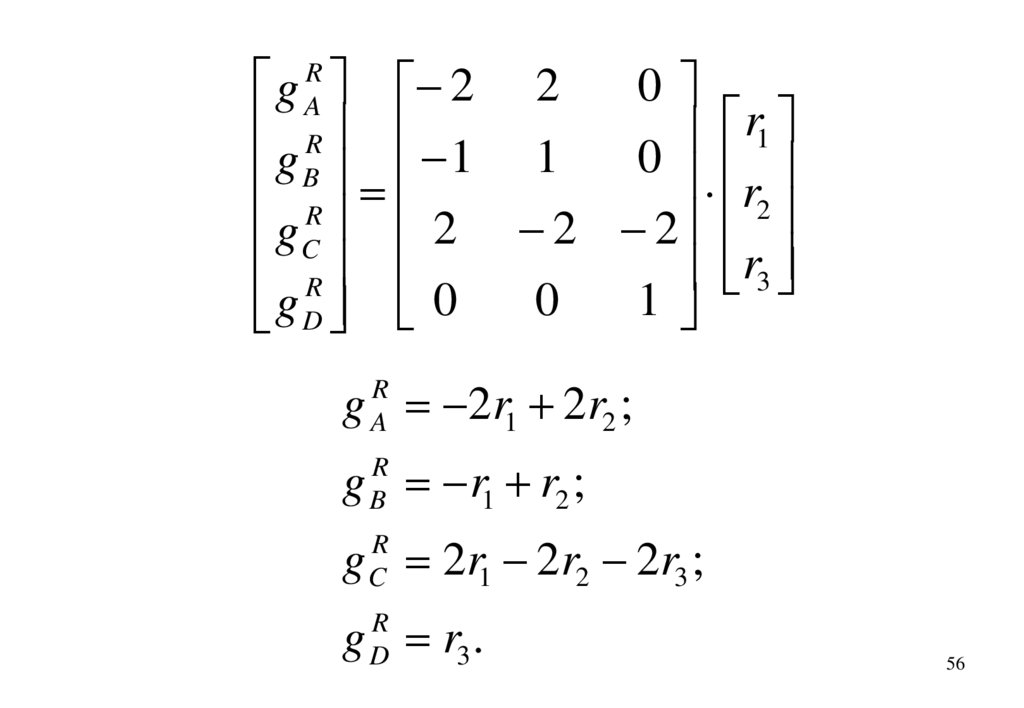






 physics
physics chemistry
chemistry