Similar presentations:
Условная оптимизация методом классического математического анализа с применением множителей
1.
1ОПТИМИЗАЦИЯ
ХИМИКО-ТЕХНОЛОГИЧЕКИХ
ПРОЦЕССОВ
С ОГРАНИЧЕНИЯМИ В ВИДЕ
РАВЕНСТВ
Модуль 2. Лекция.
Условная оптимизация методом классического
математического анализа с применением множителей
Лагранжа
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
2. Понятие условного экстремума
2Экстремум функции n переменных
R (x )
с m ограничениями (условиями) в виде равенств:
j ( x1 , x2 , ..., xn ) 0,
j 1, 2, ..., m
называется условным экстремумом.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
3.
ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА3
При решении задач оптимизации ХТП
R (x ) - критерий оптимальности
(x) 0
- уравнения математического описания
Для такой постановки задачи определения условного
экстремума необходимо выполнение условия:
n m
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
4.
ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА4
1. Решение задачи поиска условного экстремума путем
поиска безусловного экстремума:
Для определения условного экстремума целесообразно
выразить m зависимых переменных через остальные n – m
переменных:
xk f k ( xm 1 , xm 2 , ..., xn )
k 1, 2, ..., m
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
5.
ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА5
Полученные зависимости подставляются в выражение
функции R (x ) :
R R[ f1 ( xm 1 , ..., xn ),
f 2 ( xm 1 , ..., xn ), ...,
f m ( xm 1 , ..., xn ), xm 1 , xm 2 , ..., xn ]
R ( xm 1 , xm 2 , ..., xn )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
6.
ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА6
В полученной функции
независимыми.
R (x ) переменные являются
Далее обычными методами поиска безусловного
экстремума определяются значения
x
opt
m 1
,x
opt
m 2
, ..., x
т. е. находится экстремум функции
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
opt
n
R (x )
Лекционный материал «Оптимизация ХТП»
V1.0 L2
7.
ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА7
По известным значениям
x
opt
m 1
,x
opt
m 2
, ..., x
opt
n
из системы m – уравнений ограничений:
j ( x1 , x2 , ..., xn ) 0, j 1, 2, ..., m
определяются значения:
x
opt
k
f k ( xm 1 , xm 2 , ..., xn )
opt
opt
opt
k 1,...m
т.е. _ x , x , ..., x
opt
1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
opt
2
Лекционный материал «Оптимизация ХТП»
opt
m
V1.0 L2
8. 2.Поиск условного экстремума методом неопределенных множителей Лагранжа
Необходимое условие существования экстремума функциимногих переменных:
R
dxi 0
dR
i 1 xi x extr
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
8
9.
ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА9
В случае условного экстремума не все дифференциалы
будут независимыми, т.к. на переменные xi наложены
дополнительные ограничения
j ( x1 , x 2 , ..., x n ) 0,
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
dxi
j 1, 2, ..., m
Лекционный материал «Оптимизация ХТП»
V1.0 L2
10.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА10
Полный дифференциал функции
равен нулю :
j
d j
i 1 xi
n
поскольку
j (x ) в точке экстремума
dxi 0
x extr
j (x) 0
j 1,...m
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
11.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА11
Умножив обе части последнего выражения на некоторый
множитель j (j=1,…m), просуммировав и сложив с
выражением для R xi , получим:
m
n
R
j
dxi j
i 1 xi x extr
j 1
i 1 xi
n
dxi 0
x extr
или
R
m
1
2
dxi 0
1
2
m
xi
xi
xi x extr
i 1 xi
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
12.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА12
Исключим m зависимых дифференциалов таким выбором
множителей j , чтобы коэффициенты при зависимых
дифференциалах обратились в 0:
R
m
1
2
0
1
2
m
xi
xi
xi x extr
xi
i 1, 2, ..., m
Полученная система из m уравнений позволяет определить
m множителей
(если они существуют)
j
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
13.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА13
Исключив зависимые дифференциалы, получим:
R
m
1
2
dxi 0
1
2
m
xi
xi
xi x extr
i m 1 xi
со значениями j из
предыдущей системы уравнений
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
14.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА14
Для равенства последнего выражения 0 необходимо, чтобы
каждое слагаемое его было равно 0:
R
m
1
2
0
1
2
m
xi
xi
xi x extr
xi
i m 1, m 2, ..., n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
15.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА15
Объединяя условия равенства 0 зависимых и независимых
дифференциалов, получим:
R
m
1
2
1
2
m
xi
xi
xi
xi
0
x extr
i 1, 2, ..., n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
16. Одновременно должны выполняться m равенств, соответствующих ограничениям задачи:
j ( x1 , x2 , ..., xn ) 0,j 1, 2, ..., m
Таким образом для определения экстремума
Функции R c ограничениями типа равенств
необходимо решить требуемую систему (n+m)
последних уравнений относительно xi (i=1,…n) и
j (j=1,…m)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
17.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА17
Функция _ Лагранжа _
Введя функцию Лагранжа Ф, необходимые
условия экстремума которой с
производными по всем xi (i=1,…n) и j
(j=1,…m) приводят к требуемой системе
(n+m) уравнений:
m
R j j
j 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
18.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА18
Получим требуемую систему (n+m) уравнений:
0 (i 1, 2, ..., n)
x
i x extr
0
(
i
1
,
2
,
...,
m
)
extr
i x
сведя задачу к нахождению безусловного экстремума
функции Ф.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
19.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА19
ПРИМЕР 1. Классическая задача.
Определим соотношение между высотой и диаметром
цилиндрического сосуда при минимальной его поверхности и
заданном объёме.
Для этого случая:
d
R S 2π
πdH
4
2
S – поверхность цилиндра
H – высота цилиндра
d – диаметр цилиндра
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
20.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА20
2
d
H V0 0
4
V0 – заданный объём цилиндра
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
21.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА21
Записываем функцию Лагранжа:
2
d
Ф (2
dH )
4
2
d
(
H V0 )
4
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
22.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА22
Дифференцируя, получим:
Ф
dH
d H
0
d
2
dH
d H
0
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
23.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА23
Ф
d
d
0
H
4
2
d
d
0
4
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
24.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА24
Ф
d
H V0 0
4
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
25.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА25
Решая систему уравнений:
dH
d H λ
0
2
2
d
d λ
0
4
2
d
H V0 0
4
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
26.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА26
получим, что для минимальной поверхности цилиндра должно
выполняться соотношение:
d H 3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
4V0
Лекционный материал «Оптимизация ХТП»
V1.0 L2
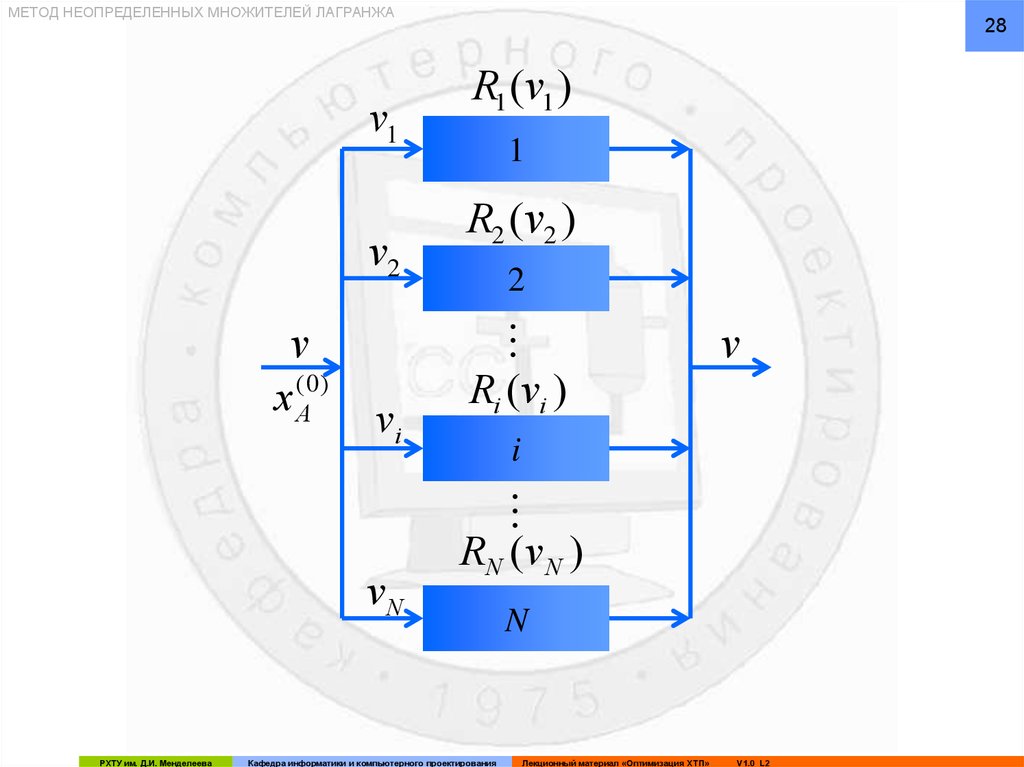
27. ПРИМЕР 2. Оптимальное распределение потока сырья между параллельно работающими аппаратами
27ПРИМЕР 2. Оптимальное распределение
потока сырья между параллельно работающими
аппаратами
Пусть общий поток (расход) сырья v, содержащий компонент
A, распределяется между N аппаратами.
Пусть Ri = Ri(vi) есть критерий оптимальности i-го аппарата и
является функцией потока vi, проходящего через этот аппарат.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
28.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖАv1
v2
v
(0 )
xA
vi
vN
РХТУ им. Д.И. Менделеева
28
R1 (v1 )
1
R2 (v2 )
2
Ri (vi )
v
i
RN (vN )
Кафедра информатики и компьютерного проектирования
N
Лекционный материал «Оптимизация ХТП»
V1.0 L2
29.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА29
Свойство аддитивности критерия оптимальности
записывается как:
N
R Ri ( v i )
i 1
Ограничение в виде равенства имеет вид:
N
v vi
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
30.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА30
Функция Лагранжа:
N
N
i 1
i 1
Ф Ri (vi ) (v vi )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
31.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖАДифференцируя и приравнивая нулю производные,
получим систему (N+1) уравнений для определения vi
(i=1,…n) и :
Ri (vi )
0
vi
vi
v vi 0
i 1
i 1, 2, ..., N
N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
31
32.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА32
Отсюда следует, что при оптимальных условиях
распределения потока в параллельно работающих аппаратах
должны выполняться равенства:
Ri Ri 1
vi vi 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
i 1, ...( N 1)
Лекционный материал «Оптимизация ХТП»
V1.0 L2
33.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА33
Задача 2
Рассчитать оптимальное распределение потока сырья v,
поступающего на параллельно работающие реакторы
идеального смешения, в которых проводится реакция типа
A P S
k1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
k2
Лекционный материал «Оптимизация ХТП»
V1.0 L2
34.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА34
В качестве критерия оптимальности использовать суммарное
количество компонента P в выходном потоке. Исходные
данные для расчёта:
число аппаратов N = 3
объёмы аппаратов, соответственно: 0,5, 0,6, 0,7 м3
расход сырья v = 3 м3/час
условия работы аппаратов - изотермические
константы скоростей k1 = 0,65 1/час; k2 = 0,3 1/час
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
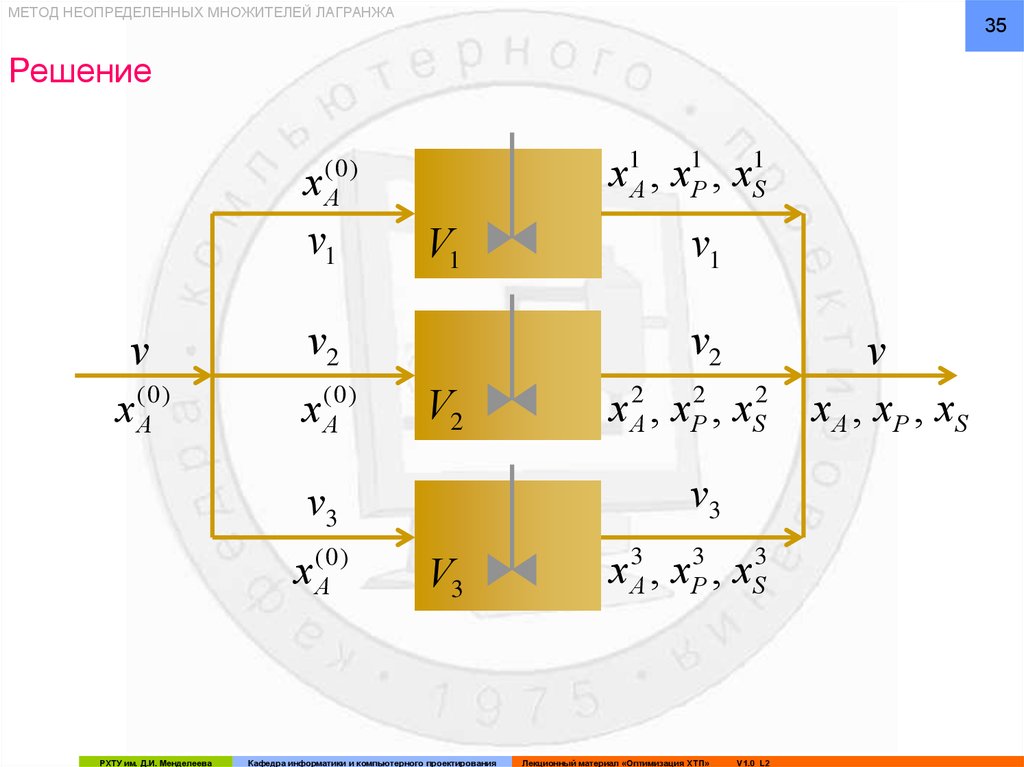
35.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА35
Решение
x ,x ,x
1
A
(0 )
A
x
v1
v
(0 )
xA
V1
x
v2
V2
РХТУ им. Д.И. Менделеева
x ,x ,x
2
A
2
P
2
S
v3
v3
x A(0 )
1
S
v1
v2
(0 )
A
1
P
V3
Кафедра информатики и компьютерного проектирования
x 3A , xP3 , xS3
Лекционный материал «Оптимизация ХТП»
V1.0 L2
v
x A , x P , xS
36.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА36
Критерий оптимальности для всей системы есть:
N
R v xP vi x
i 1
i
P
Количество вещества P на выходе из i-го реактора:
vi x Ri
i
P
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
37.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА37
Уравнение ограничений на процесс:
N
φ v vi 0
i 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
38.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА38
При оптимальных условиях должно выполняться равенства:
Ri Ri 1
vi vi 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
i 1, 2
Лекционный материал «Оптимизация ХТП»
V1.0 L2
39.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА39
Вычислим значение производной:
Ri
x
i
xP vi
vi
vi
i
P
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
40.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА40
Уравнения материального баланса по компонентам A и P для
i-го реактора с расходом потока в нем vi и его объемом Vi
k1
k2
для реакции A
P
S , где k , k2 - константы
1
скоростей реакции :
vi ( x
( 0)
A
x ) Vi k1 x 0
i
A
i
A
vi x Vi (k1 x k2 x ) 0
i
P
РХТУ им. Д.И. Менделеева
i
A
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
i
P
V1.0 L2
41.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА41
Уравнения материального баланса по компонентам A и P для
i-го реактора с использованием времени пребывания в
реакторе i имеют вид :
x
( 0)
A
x i k1 x 0
i
A
i
A
x i (k1 x k 2 x ) 0
i
P
i
A
i
P
i Vi vi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
42.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА42
Из полученной системы уравнений выразим концентрацию
компонента P в i – том аппарате через начальную
концентрацию компонента A:
i x k1
x
(1 i k1 ) (1 i k 2 )
(0)
A
i
p
x
x i
vi i vi
i
p
РХТУ им. Д.И. Менделеева
i
p
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
43.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА43
Тогда:
k1 i (k1 k 2 1)
x
(0)
xA
2
vi
vi [(1 i k1 ) (1 i k2 )]
2
i
i
P
Vi
i
vi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
44.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА44
Из полученного выражения следует, что произведение
vi
x
i
p
vi
vi
x
i
p
vi
( i )
зависит от времени пребывания i ,а также из уравнений
материальных балансов следует тоже зависимость только от
времени пребывания i :
x x ( i )
i
p
РХТУ им. Д.И. Менделеева
i
p
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
45.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА45
Так как в выражении для рассматриваемой реакции :
Ri
x
i
xP vi
vi
vi
i
P
оба слагаемых зависят от
РХТУ им. Д.И. Менделеева
i
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
46.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖАа также поскольку:
46
Ri Ri 1
vi vi 1
то будет справедливо:
Ri
f ( i )
vi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Ri 1
f ( i 1 )
vi 1
Лекционный материал «Оптимизация ХТП»
V1.0 L2
47.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА47
и имеем:
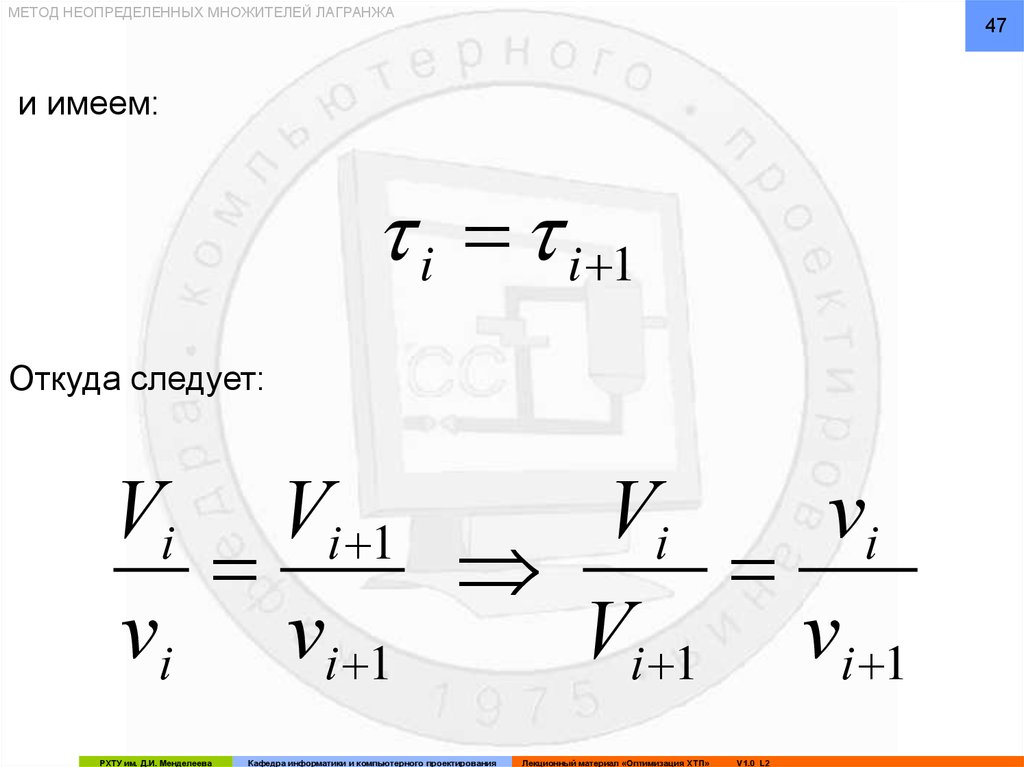
i i 1
Откуда следует:
Vi Vi 1
Vi
vi
Vi 1 vi 1
vi vi 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
48.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА48
Получаем систему уравнений для расчёта распределения
потоков:
V1 v1
V2 v2
V2 v2
V3 v3
v1 v2 v3 v
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
49.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА49
Подставляя исходные данные, получим:
0,5 v1
0,6 v2
0,5 v2 0,6 v1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
50.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА50
Подставляя исходные данные, получим:
0,6 v2
0,7 v3
0,6 v3 0,7 v2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
51.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА51
Подставляя исходные данные, получим:
0,6
0,7 0,6
v1
v1
v1 3
0,5
0,6 0,5
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
52.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА52
Откуда находим:
v1 0,833 м / час
3
v2 1,0 м / час
3
v3 1,167 м / час
3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
53. ПРИМЕР 3. Оптимизация многостадийных процессов
53Рассмотрим многостадийный процесс, состоящий из стадий,
каждая из которых описывается системой конечных
уравнений вида:
i 1
1
i 1
2
i 1
n
x φ ( x , x , ..., x , u , u , ..., u )
i
k
i
k
i
1
i
2
k 1, 2, ..., n
i – номер стадии
k – номер переменной
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
i
r
54.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖАx (0 )
x1
1
u1
54
x 2 x i 1
2
u2
x i x N 1
N
i
ui
xN
uN
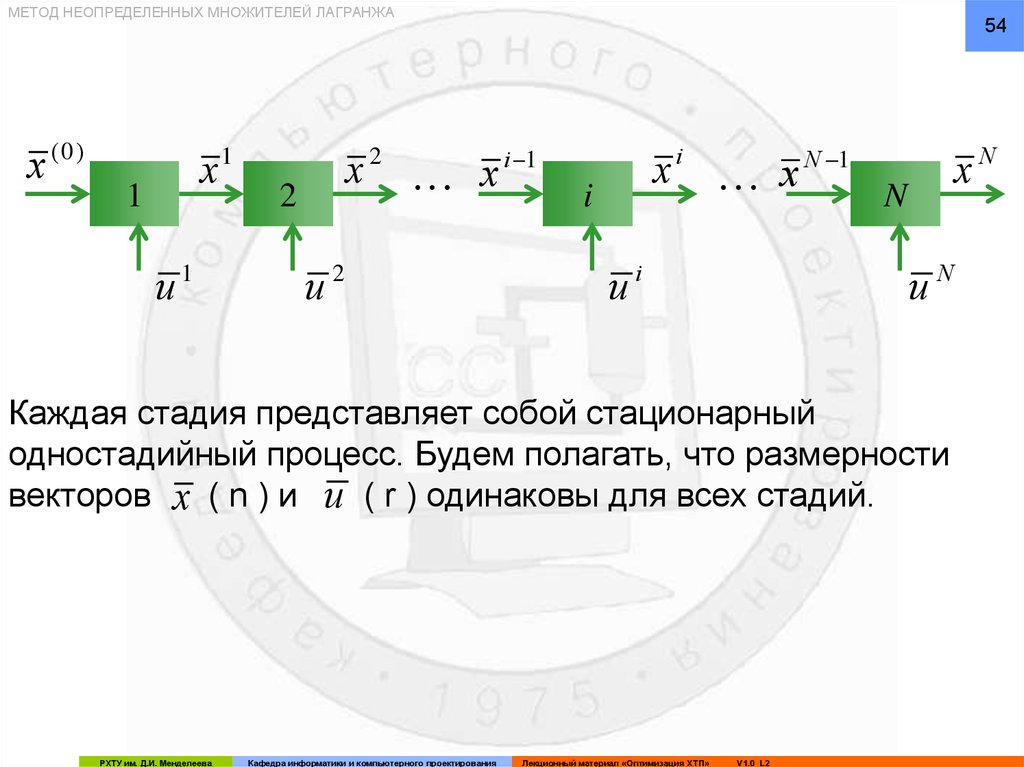
Каждая стадия представляет собой стационарный
одностадийный процесс. Будем полагать, что размерности
векторов x ( n ) и u ( r ) одинаковы для всех стадий.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
55.
55Условные обозначения на схеме каскада аппаратов:
N - число стадий процесса (аппаратов)
x i - вектор переменных состояния процесса на выходе
из i-того аппарата и на входе в i+1 аппарат
u i - вектор переменных управления i-том аппарате
ri - частный критерий оптимальности в i-том аппарате
N
R ri - критерий оптимальности всего процесса –
i 1
аддитивная функция в общем случае
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
56.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА56
Пусть критерий оптимальности многостадийного процесса
задан в виде некоторой функции только от выходных
параметров последней стадии:
R R( x ) R( x , x , ..., x )
N
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
N
1
N
2
Лекционный материал «Оптимизация ХТП»
V1.0 L2
N
n
57.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА57
Уравнения математической модели могут быть записаны в
неявной форме:
(x , x , u ) 0
i
k
i 1
i
i
i 1, 2, ..., N
k 1, 2, ..., n
и могут рассматриваться как уравнения ограничений.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
58.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА58
При использовании метода неопределённых множителей
Лагранжа для решения задачи оптимизации соотношения
математической модели на всех стадиях используются как
ограничения, наложенные на переменные, часть из которых
входит в выражение для критерия оптимальности:
i
1
i
2
i
n
i
1
i
2
x , x , ..., x , u , u , ..., u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
i
r
59.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА59
Составим функцию Лагранжа:
N
n
Φ R( x ) λ φ ( x , x , u )
N
i 1 k 1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
i
k
i
k
Лекционный материал «Оптимизация ХТП»
i 1
V1.0 L2
i
i
60.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА60
При дифференцировании функции Лагранжа по всем
переменным получим три типа уравнений:
дифференцирование по
x Nj:
R( x )
, x ,u )
N ( x
0
k
N
N
N
x j
x j
x j
k 1
N
n
N
k
N 1
N
j 1,...n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
N
61.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖАдифференцирование по
61
xij (i 1, 2, ..., N 1) :
(x , x , u )
i 1
k
i
i
x j k 1
x j
i 1
k
n
i 1
i
i 1
( x , x , u )
0
i
x j
k 1
n
i
k
i
k
i 1
i
i
j 1,...n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L2
62.
МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖАдифференцирование по
62
u ( 1, 2, ..., r; :i 1,...N )
i
, x ,u )
i ( x
0
k
i
i
u k 1
u
r
i
k
i 1
i
i
Для нахождения оптимума полученная система из трёх
последних систем уравнений должна решаться совместно с
уравнениями математической модели, которые получаются
при дифференцировании по всем






















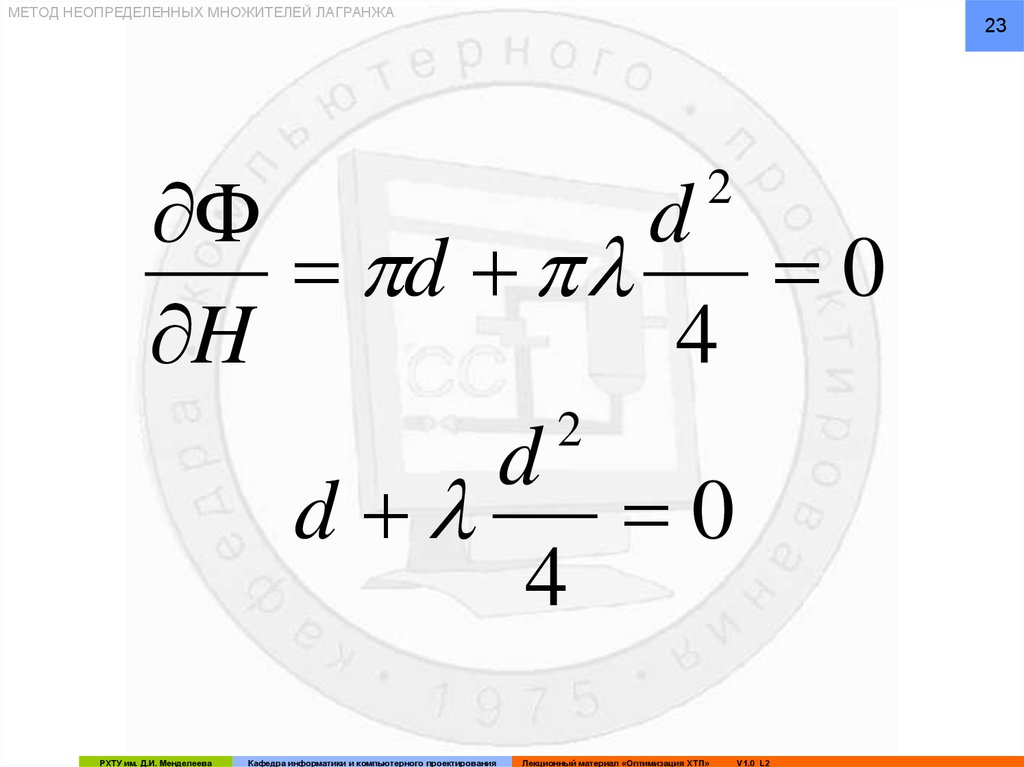
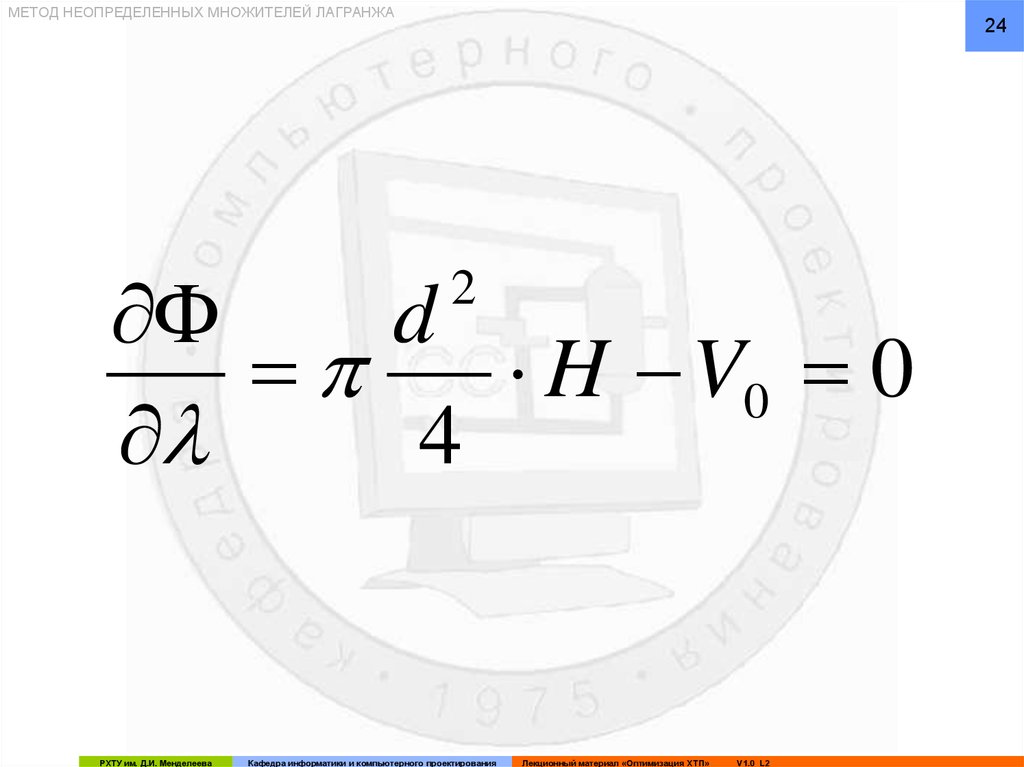
























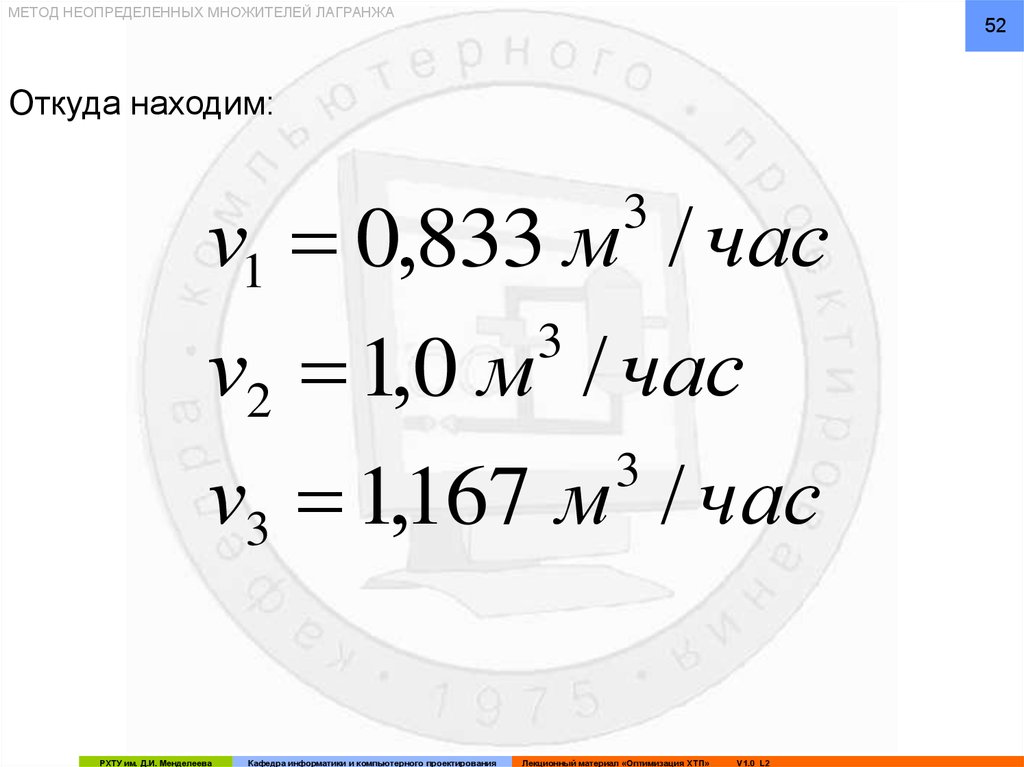
























 mathematics
mathematics chemistry
chemistry








