Similar presentations:
Методы поиска условного экстремума
1. Методы поиска условного экстремума
МЕТОДЫПОИСКА
УСЛОВНОГО
ЭКСТРЕМУМА
ВЫПОЛНИЛ: ШЕЛОМЕНЦЕВ ВЛАДИСЛАВ
ИХПБДИТБ 1 КУРС МАГ.
2. УСЛОВНЫЙ ЭКСТРЕМУМ
Точка (х0,у0) называется точкой условногоэкстремума (максимума или минимума),
если существует такая окрестность этой
точки, что для всех точек (х,у) из этой
окрестности, удовлетворяющих условию
g(x,y)=C, выполняется неравенство:
f ( x0 , y0 ) f ( x, y )
f ( x0 , y0 ) f ( x, y)
max
min
3. УСЛОВНЫЙ ЭКСТРЕМУМ
Условный экстремум является точкойлокального максимума, как на данном
рисунке (или минимума) функции.
4. УСЛОВНЫЙ ЭКСТРЕМУМ
Существует два основных метода поискаусловного экстремума:
Метод замены переменной
Метод множителей Лагранжа
5. Метод замены переменной
МЕТОД ЗАМЕНЫ ПЕРЕМЕННОЙРассмотрим нахождение экстремума
функции нескольких переменных не на всей
области определения, а на множестве,
удовлетворяющему некоторому условию.
Пусть задана функция z=f(x,y), аргументы
которой удовлетворяют уравнению
g(x,y)=C,
называемому уравнением связи.
6. Метод замены переменной
МЕТОД ЗАМЕНЫ ПЕРЕМЕННОЙЧтобы найти условный экстремум, нужно из
уравнения связи выразить одну
переменную через другую:
y=φ(x).
Подставим это выражение в функцию двух
переменных и получим функцию одной
переменной:
z=f(x,y)=f(x, φ(x)).
Ее экстремум и будет условным
экстремумом функции z=f(x,y).
7. Метод замены переменной (пример)
МЕТОД ЗАМЕНЫ ПЕРЕМЕННОЙ(ПРИМЕР)
Найти точки максимума и минимума функции
z x 2y
2
2
при условии 3х+2у=11.
8. Метод замены переменной (решение)
МЕТОД ЗАМЕНЫ ПЕРЕМЕННОЙ(РЕШЕНИЕ)
3x 2 y 11
2
11 3x
y
2
11 2
11 3 x
z x 2
x 6 x 11
2
2
2
z 11 x 3
x0 3
y0 1
условный минимум
9. УСЛОВНЫЙ ЭКСТРЕМУМ
В этом примере связь между х и у оказаласьлинейной, поэтому уравнение связи легко
разрешилось относительно одной из
переменных.
Но в некоторых случаях это сделать
довольно сложно. Поэтому в общем случае
для нахождения условного экстремума
используется метод множителей Лагранжа.
10. метод множителей Лагранжа
МЕТОД МНОЖИТЕЛЕЙЛАГРАНЖА
Рассмотрим функцию трех переменных:
L ( x, y , ) f ( x, y ) ( g ( x, y ) C )
Функция Лагранжа
11. метод множителей Лагранжа (теорема)
МЕТОД МНОЖИТЕЛЕЙЛАГРАНЖА (ТЕОРЕМА)
Если точка (х0,у0) является точкой
условного экстремума функции z=f(x,y)
при условии g(x,y)=C, то существует
значение λ0, такое что точка
(х0,у0,λ0) является точкой экстремума
функции L(x,y,λ).
12. метод множителей Лагранжа
МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖАСледовательно, для нахождения условного
экстремума функции z=f(x,y) при условии
g(x,y)=C, требуется найти решение системы:
Lx f x ( x, y ) g x ( x, y ) 0
L y f y ( x, y ) g y ( x, y ) 0
L
g
( x, y ) C 0
Последнее уравнение совпадает с
уравнением связи.
13. метод множителей Лагранжа
МЕТОД МНОЖИТЕЛЕЙЛАГРАНЖА
Первые два уравнения можно записать в
виде:
gradf gradg
То есть в точках условного экстремума
градиенты функций f(x,y) и g(x,y)
коллинеарны.
14. метод множителей Лагранжа
МЕТОД МНОЖИТЕЛЕЙЛАГРАНЖА
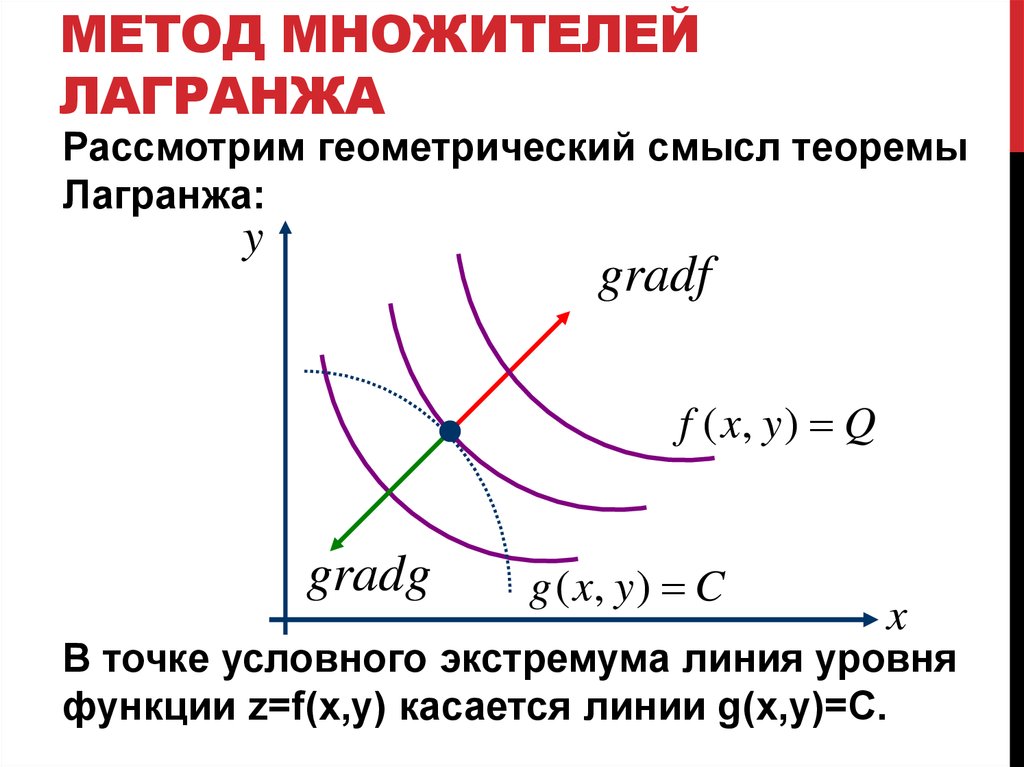
Рассмотрим геометрический смысл теоремы
Лагранжа:
y
gradf
f ( x, y ) Q
gradg
g ( x, y ) C
x
В точке условного экстремума линия уровня
функции z=f(x,y) касается линии g(x,y)=C.
15. Спасибо за внимание
СПАСИБО ЗАВНИМАНИЕ
Выполнил: Шеломенцев Владислав Валерьевич
ИХПБДиТБ 1 курс маг.














 mathematics
mathematics








