Similar presentations:
Безусловная оптимизация методом классического математического анализа. Определение оптимального времени пребывания
1.
1Модуль 1. Семинар 1.
Безусловная оптимизация методом классического
математического анализа
Определение оптимального времени пребывания в
непрерывном реакторе с мешалкой
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
2.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ2
Задача 1
Рассчитать оптимальное время проведения химической
реакции в аппарате идеального смешения, приняв в качестве
критерия оптимальности выход целевого продукта P.
Схема реакции:
A P S
k1
k2
Порядок обеих стадий реакции – первый. Константы
скоростей равны:
k1 0,35 час
РХТУ им. Д.И. Менделеева
1
Кафедра информатики и компьютерного проектирования
k2 0,13 час
Лекционный материал «Оптимизация ХТП»
V1.0 L1
1
3.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ3
Решение
Материальный баланс по компонентам A и P:
v( x x A ) Vk1 x A 0
vx
V
(
k
x
k
x
)
0
P
1 A
2 P
( 0)
A
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
4.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ4
При делении уравнений на расход реагента v получаем:
x x A k1 x A 0
xP (k1 x A k2 xP ) 0
( 0)
A
где
V v
РХТУ им. Д.И. Менделеева
- среднее время пребывания
реагентов в реакторе
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
5.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ5
Выход продукта P выражается:
xP
k1
P (0)
xA
(1 k1 ) (1 k 2 )
Необходимое условие существования экстремума:
d P
0
d
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
6.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ6
d P
k1 (1 k1 k2 )
2
d
[(1 k1 ) (1 k2 )]
2
Поскольку
и
[(1 k1 ) (1 k2 )] 0
2
k1 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
7.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ7
Условие экстремума будет иметь вид:
1 k1 k2 (
) 0
опт 2
Откуда:
РХТУ им. Д.И. Менделеева
опт
1
k1 k 2
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
8.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙmax
P
опт
8
1
4,7 часа
0,35 0,13
k1
0,35
0
,
39
2
2
( k1 k 2 )
( 0,35 0,13 )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
9.
9Модуль 1. Семинар 2.
Безусловная оптимизация методом классического
математического анализа.
Определение оптимальной температуры в
непрерывном реакторе с мешалкой
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
10.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ10
Задача 2
Рассчитать оптимальную температуру проведения обратимой
двухкомпонентной реакции в реакторе с мешалкой,
использовав в качестве критерия оптимальности выход
целевого продукта P.
Схема реакции:
k1
A
P
k2
Порядок обеих стадий реакции – первый. Константы равны:
A1 70 мин
РХТУ им. Д.И. Менделеева
1
Кафедра информатики и компьютерного проектирования
A2 100 мин
Лекционный материал «Оптимизация ХТП»
V1.0 L1
1
11.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ11
Задача 3
Значения энергий активации стадий реакции:
кал
кал
E2 5000
E1 2500
моль
моль
Время пребывания в реакторе:
10 мин
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
12.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ12
Решение
Материальный баланс по компонентам А и P для реактора
идеального перемешивания:
v ( x x A ) V (k1 x A k2 xP )
v xP V (k1 x A k2 xP )
( 0)
A
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
13.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ13
Из системы уравнений материального баланса определяется
выражение для выхода компонента P:
P
где
1 (k1 k 2 )
V v
k1 A1e
РХТУ им. Д.И. Менделеева
k1
E1
- среднее время пребывания
реагентов в реакторе
RT
Кафедра информатики и компьютерного проектирования
k2 A2e
Лекционный материал «Оптимизация ХТП»
V1.0 L1
E2
RT
14.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ14
Необходимое условие существования экстремума:
dk1
dk1 dk2
[1 (k1 k2 )] (
) k1
d P
dT dT
dT
0
2
dT
[1 (k1 k 2 )]
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
15.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ15
Приравнивая числитель последнего выражения к нулю,
получаем:
dk1
dk 2
(1 k 2 )
k1 0
dT
dT
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
16.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙУчитывая, что:
16
dk
E
k
2
dT
RT
Получаем:
E1
E2
k1
(1 k 2 ) k2
k1
опт 2
опт 2
R (T )
R (T )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
17.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ17
Из последнего выражения следует:
E1
k2
( E2 E1 )
или
A2 e
РХТУ им. Д.И. Менделеева
E2
RT опт
E1
( E2 E1 )
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
18.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ18
Логарифмирование последнего выражения даёт:
E2
E1
ln A2
ln
опт
RT
( E2 E1 )
T
опт
РХТУ им. Д.И. Менделеева
E2
E2
R ln [ A2 ( 1)]
E1
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
19.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ19
Подставляя численные значения параметров, получаем:
T
опт
5000
5000
1,98 ln [10 100(
1)]
2500
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
366 K
o
V1.0 L1
20.
20Модуль 1. Семинар 3.
Безусловная оптимизация методом классического
математического анализа.
Определение оптимального времени протекания
процесса в периодическом реакторе с мешалкой
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
21.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ21
Задача 3
Рассчитать оптимальное время проведения реакции в
периодическом реакторе с мешалкой, использовав в качестве
критерия оптимальности выход целевого продукта P.
Схема реакции:
A P S
k1
k2
Порядок обеих стадий реакции – первый. Константы
скоростей равны:
k1 0,35 час
РХТУ им. Д.И. Менделеева
1
Кафедра информатики и компьютерного проектирования
k2 0,13 час
Лекционный материал «Оптимизация ХТП»
V1.0 L1
1
22.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ22
Решение
Материальный баланс по компонентам A и P для
периодического реактора:
dx A
k
x
1
A
dt
dx
P k1 x A k2 xP
dt
Начальные условия:
x A t t ( 0 ) x
(0)
A
x P t t ( 0 ) 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
23.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ23
Первое уравнение системы – с разделяющимися
переменными:
dx A
k1 dt
xA
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
24.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ24
При интегрировании получаем:
xA
t
dx A
k
d
t
1
( 0 ) x A
0
x
A
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
25.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ25
xA
ln ( 0 ) k1 t
xA
Откуда следует:
xA x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
( 0)
A
e
k1 t
Лекционный материал «Оптимизация ХТП»
V1.0 L1
26.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ26
Полученное соотношение подставляется во второе уравнение
системы:
dxP
k1 t
( 0)
k2 xP k1 x A e
dt
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
27.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ27
При делении обеих частей полученного выражения на x
получаем дифференциальное уравнение относительно
выхода
P :
d P
k1 t
k2 P k1 e
dt
С начальными условиями:
t 0
P 0
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
(0)
A
28.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ28
Решение полученного дифференциального уравнения
стандартными методами даёт:
k1
k 2 t
k1 t
P
(e
e )
k1 k2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
29.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ29
Необходимое условие существования экстремума:
d P
k1
k 2 t
k1 t
( k2 e
k1 e ) 0
dt
k1 k2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
30.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙПоскольку
30
k1 k2 , получаем:
k1e
РХТУ им. Д.И. Менделеева
k1 t
k2 e
Кафедра информатики и компьютерного проектирования
k2 t
Лекционный материал «Оптимизация ХТП»
0
V1.0 L1
31.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ31
Логарифмирование последнего выражения даёт:
t
t
опт
опт
ln k1 k2
k1 k2
ln 0,35 0,13
4,5 часа
0,35 0,13
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
32.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ32
Подставляя t опт в выражение для
P , получаем
максимально возможный выход целевого продукта P для
реактора периодического действия:
max
P
0,35
0,13 4, 5
0, 35 4, 5
(e
e
) 0,56
0,35 0,13
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
33.
33Модуль 1. Семинар 4.
Безусловная оптимизация методом классического
математического анализа.
Определение оптимального расхода хладагента в
теплообменнике смешение-смешение
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
34.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ34
Задача 4
Рассчитать оптимальный расход хладагента в теплообменнике смешениесмешение и определить площадь поверхности теплопередачи при
следующих параметрах процесса:
1. Горячий теплоноситель – расход 6 кг/вр; теплоемкость 4190 Дж/кг*С;
температура на входе и на выходе потока 112.5С и 85.7С
2. Холодный поток – диапазон изменения расхода 1 – 10 кг/вр;
теплоемкость 3000 Дж/кг*С; температура на входе потока 20С
3. Коэффициент теплопередачи 500 Вт/м2*С
4. В качестве критерия оптимальности использовать приведенные
затраты на процесс, определяемые по формуле
R 1 (площадь поверхности теплопередачи )
10 ( расход холодного теплоносителя )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
35.
Поверочно-оценочный расчет35
Математическое описание
vCp (T
( 0)
T ) K F (Tx T ) 0
( 0)
x
vxC px (T
T
T
Tx ) K F (T Tx ) 0
T
T
Необходимо определить Т = ? и Тх = ?
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
36.
36Для решения задачи оптимизации необходим
конструкционный расчет
Математическое описание преобразуется и записывается с
учетом общего теплового баланса
vCp (T
( 0)
T ) K F (Tx T ) 0
vCp (T
( 0)
T ) vxC px (T
T
T
( 0)
x
Tx ) 0
Необходимо определить: F T = ? Vx = ?
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
37.
37Решение методом подстановки:
второе уравнение СЛАУ решается относительно Tx
Tx T
(0)
x
РХТУ им. Д.И. Менделеева
(T
Кафедра информатики и компьютерного проектирования
(0)
T)
Лекционный материал «Оптимизация ХТП»
vCp
vx C px
V1.0 L1
38.
38затем выражение для Tx подставляется в первое уравнение СЛАУ, которое
решается относительно FT:
vC
p
T
T
(0)
(0)
K F Tx (T T )
T
v x C px
(0)
vCp (T T )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
39.
39F
vCp (T T
T
(0)
)
vC
p
T
( 0)
(0)
K Tx (T T )
T
v x C px
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
40.
40Производя преобразования в знаменателе последнего
выражения и вынося за скобки
vCp (T T ),
(0)
получим:
F
vxC px
T
РХТУ им. Д.И. Менделеева
(0)
v
C
x px
T T Tx
K (0)
1
T T vC
p
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
41.
41Обозначим
T T
γ (0)
T T
(0)
x
Тогда условием физической реализуемости данного
теплообменника будет:
γ
РХТУ им. Д.И. Менделеева
v x C px
vCp
Кафедра информатики и компьютерного проектирования
1
Лекционный материал «Оптимизация ХТП»
V1.0 L1
42.
42Система двух уравнений в конструкционном расчете
решалась относительно Tx и FT.
Это означает, что температура T на выходе из
теплообменника и, соответственно, тепловая нагрузка Q
Q vCp (T
( 0)
T )
при определении Tx и FT известны и заданы.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
43.
Оптимизация теплообменника типасмешение-смешение
А) Критерий оптимальности - экономический
R C x v x C F F min
T
Cx – стоимость единицы расхода хладагента [руб/ед. массы] (в случае задания
массового расхода)
CF - стоимость единицы площади поверхности теплообменника, исчисляемая с
учетом амортизации теплообменника [руб/(м2∙ед. времени)]
В) Таким образом, ресурсами оптимизации –
оптимизирующими переменными – являются vx и FT
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
43
44.
44Однако, из предыдущих выводов следует, что
F F (v x )
T
T
Поэтому достаточно воспользоваться необходимым условием
функции одной переменной:
R (v x ) C x v x C F F (v x )
T
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
45.
45Необходимое условие экстремума имеет вид:
R
dF
C x CF
0
vx
dvx
T
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
46.
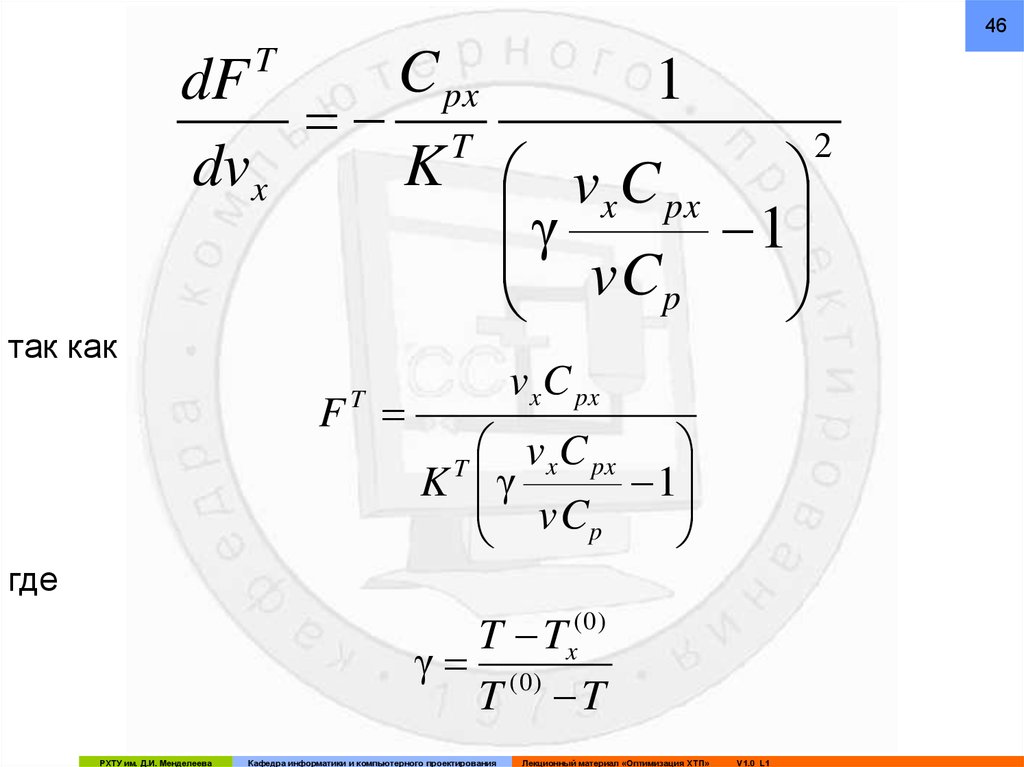
46T
так как
C px
dF
1
T
2
dvx
K vC
x px
γ
1
vC
p
F
v x C px
T
v x C px
K γ
1
vC
p
T
где
T Tx( 0)
γ ( 0)
T T
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
47.
47При подстановке полученной производной в необходимое
условие существования экстремума R получается:
C x CF
РХТУ им. Д.И. Менделеева
C px
1
T
K vC
x px
γ
1
vC
p
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
2
48.
48или
2
v x C px
C F C px
γ
1
T
vC
C
K
p
x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
49.
49Отсюда можно определить:
γ
vxC px
РХТУ им. Д.И. Менделеева
vCp
1
Кафедра информатики и компьютерного проектирования
CF C px
Cx K
Лекционный материал «Оптимизация ХТП»
V1.0 L1
T
50.
50или
vCp
C F C px
1
vx
T
γC px
C x K
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
51.
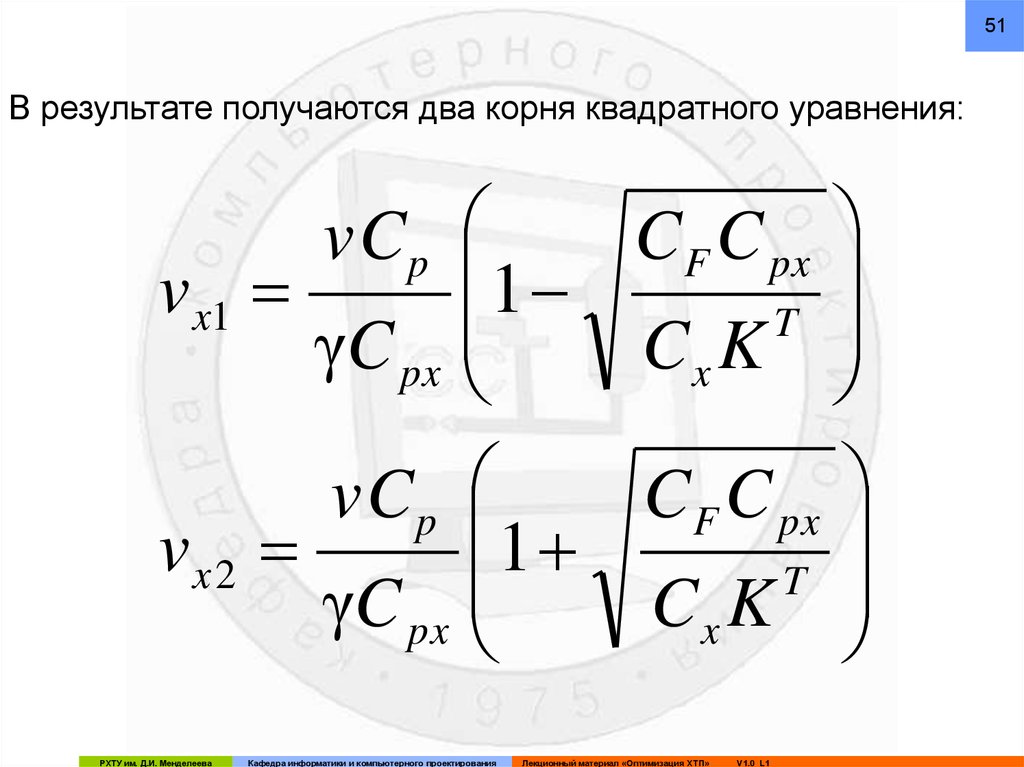
51В результате получаются два корня квадратного уравнения:
vC p
C F C px
v x1
1
T
γC px
Cx K
vC p
C F C px
1
vx 2
T
γC px
Cx K
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
52.
52Учитывая то обстоятельство, что оптимальное значение
может быть в тех точках, где производная целевой функции R
не существует, что соответствует обращению в ноль
знаменателя dFT/dvx, можно записать третье возможное
решение:
vx3
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
vC p
γC px
Лекционный материал «Оптимизация ХТП»
V1.0 L1
53.
53Для каждого из этих решений необходимо проверить
достаточное условие существования экстремума.
Данное достаточное условие целесообразно проверять,
исходя из физического смысла решаемой задачи, т.е.
физической реализуемости теплообменника – исходя из
выражения:
F
v x C px
T
РХТУ им. Д.И. Менделеева
v
C
x px
T
K γ
1
vC
p
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
54.
54Отсюда следует, что должно выполняться неравенство:
vx
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
vC p
γC px
Лекционный материал «Оптимизация ХТП»
V1.0 L1
55.
55При этих условиях производная dFT/dvx является монотонно
возрастающей функцией, и достаточное условие
существования экстремума выполняется.
Из трех возможных решений только vx2 удовлетворяет
последнему неравенству.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
56.
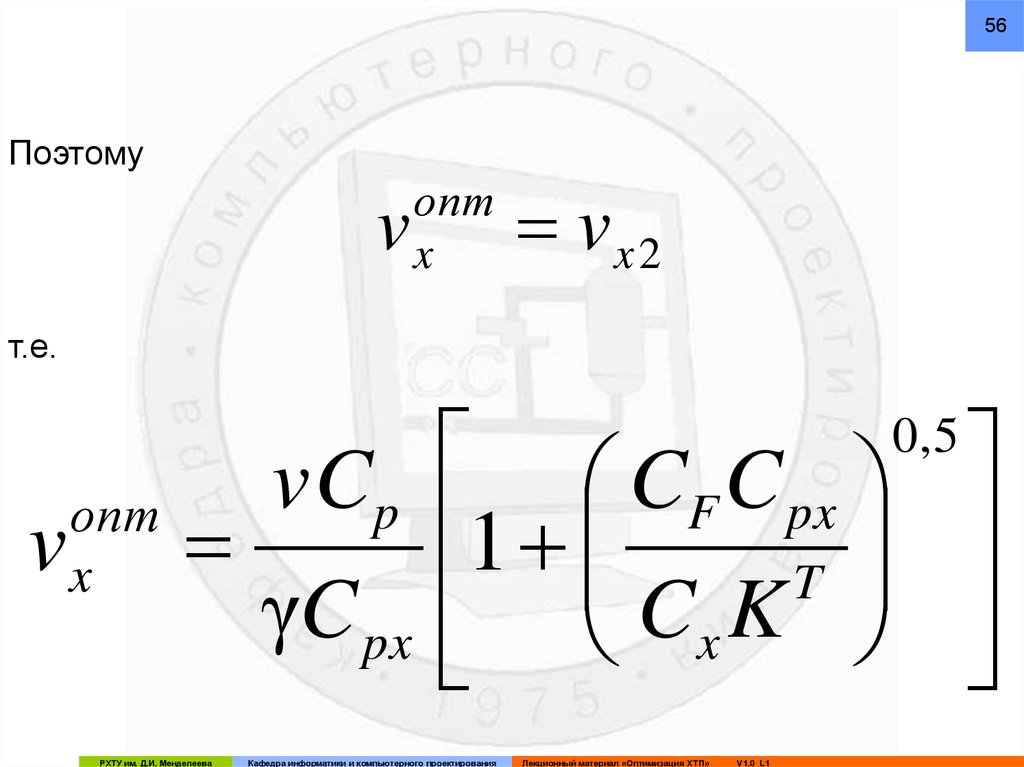
56Поэтому
v
опт
x
vx 2
т.е.
vC
C
C
p
F
px
опт
vx
1
T
γC px Cx K
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
0,5
57.
57После подстановки выражения для оптимального значения vx
в выражение для FT(vx) получается:
F
T ( опт)
РХТУ им. Д.И. Менделеева
T
Cx K
vCp
1
T
γK CF C px
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
0,5
58.
58Значение Rmin определяется по формуле:
R
min
РХТУ им. Д.И. Менделеева
C v
опт
x x
Кафедра информатики и компьютерного проектирования
CF F
Лекционный материал «Оптимизация ХТП»
V1.0 L1
T ( опт)























































 mathematics
mathematics chemistry
chemistry