Similar presentations:
Теория принятия решений принятие оптимальных решений методами динамического программирования
1. Теория принятия решений принятие оптимальных решений методами динамического программирования
ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙПРИНЯТИЕ ОПТИМАЛЬНЫХ
РЕШЕНИЙ МЕТОДАМИ
ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Лекция 2.8
2. СОДЕРЖАНИЕ
Текущий контроль знанийЧасть 1. Общие принципы динамического
программирования.
Часть 2. Принятие решений на моделях,
сводимых к задачам дискретной оптимизации с
булевыми переменными.
Часть 3. Принятие решений на моделях,
сводимых к задачам дискретной оптимизации с
небулевыми переменными.
Часть 4. Принятие решений на моделях
оптимального упорядочения.
3. ТЕКУЩИЙ КОНТРОЛЬ ЗНАНИЙ
На бихроматическом графе G(X,U), │Х│= 8,│Х₁│=│Х₂│=4, матрица которого приведенаниже, определить оптимальное распределение работ при условии, что:
1. Минимизируется время выполнения плана, при условии, что фонд зарплаты равен:
S= 4 ∙max{│k-5│; │k-25│}.
2. Минимизируются затраты на выполнение плана при условии, что время его выполнения не
превышает величины Т= max{│k-15│;│k-35│}.
3. Минимизируются затраты на выполнение плана при условии, что время его выполнения не
ограничено.
1
2
3
4
1
│k-5│;│k-15│
│k-10│;│k-25│
│k-7│;│k-17│
│k-8│;│k-15│
2
│k-3│;│k-30│
│k-25│;│k-15│
│k-2│;│k-19│
│k-4│;│k-32│
3
│k-31│;│k-15│
│k-6│;│k-14│
│k-3│;│k-35│
│k-23│;│k-25│
4
│k-16│;│k-14│
│k-35│;│k-5│
│k-11│;│k-10│
│k-5│;│k-15│
4. ЧАСТЬ 1
Общие принципыдинамического
программирования
5. ОПРЕДЕЛЕНИЕ
Динамическое программированиепредставляет собой многошаговый
процесс принятия решений,
направленных на достижение единой
цели. При этом на каждом шаге этого
процесса решается задача меньшей
размерности, чем исходная.
6. Принцип оптимальности Беллмана
Оптимальная стратегия обладает темсвойством, что независимо от начального
состояния и начального решения задачи,
последующие решения должны составлять
оптимальную стратегию лишь в
рассматриваемый момент времени. Иными
словами оптимальная стратегия в каждый
момент времени определяется лишь
состоянием системы, но не ее предысторией.
7. Часть 2
Принятие решений намоделях, сводимых к
задачам дискретной
оптимизации с
булевыми переменными
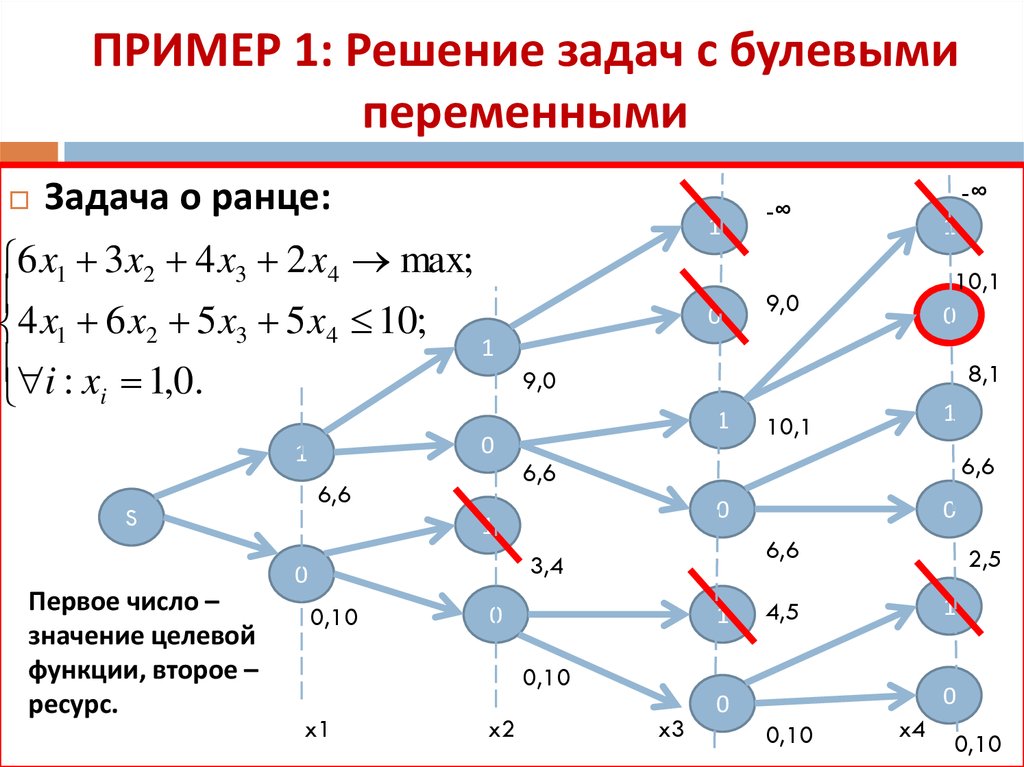
8. ПРИМЕР 1: Решение задач с булевыми переменными
Задача о ранце:6 x1 3 x2 4 x3 2 x4 max;
4 x1 6 x2 5 x3 5 x4 10; 1
i : x 1,0.
i
0
1
6,6
S
Первое число –
значение целевой
функции, второе –
ресурс.
1
0
10,1
0
9,0
8,1
1
1
10,1
6,6
6,6
0
0
6,6
3,4
0,10
1
9,0
1
0
-∞
-∞
0
1
2,5
1
4,5
0,10
x1
x2
x3
0
0
0,10
x4
0,10
9. САМОСТОЯТЕЛЬНО
Пользуясь методом динамическогопрограммирования, решить задачу о ранце:
4 x1 7 x2 9 x3 3 x4 max;
6 x1 5 x2 8 x3 7 x4 12;
i : x 1,0.
i
10. ЧАСТЬ 3
Принятие решений намоделях, сводимых к
задачам дискретной
оптимизации с
небулевыми
переменными
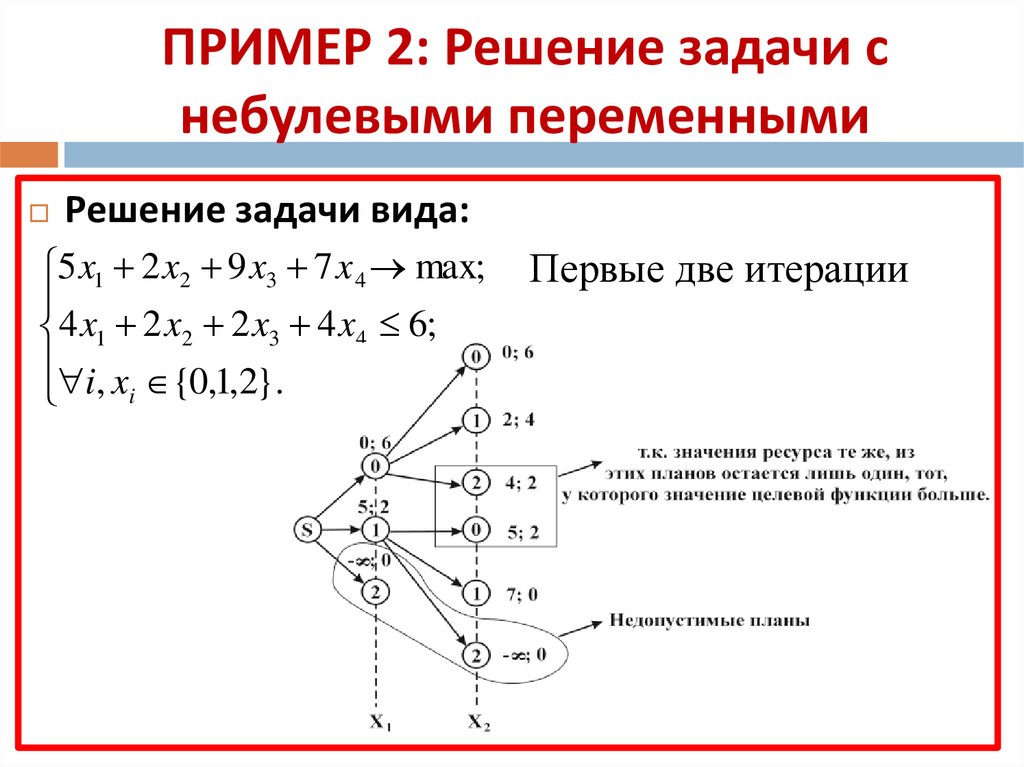
11. ПРИМЕР 2: Решение задачи с небулевыми переменными
Решение задачи вида:5 x1 2 x2 9 x3 7 x 4 max;
4 x1 2 x2 2 x3 4 x4 6;
i, x {0,1,2}.
i
Первые две итерации
12. ПРИМЕР 2 (ПРОДОЛЖЕНИЕ)
Третья итерация:5 x1 2 x2 9 x3 7 x 4 max;
4 x1 2 x2 2 x3 4 x4 6;
i, x {0,1,2}.
i
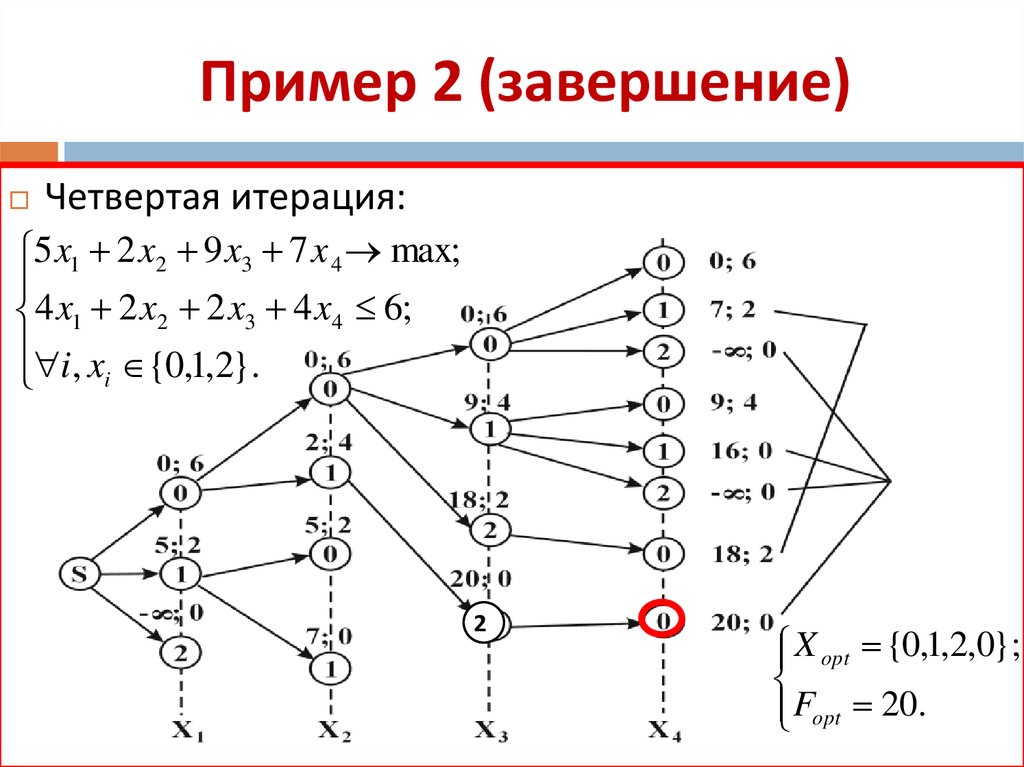
13. Пример 2 (завершение)
Четвертая итерация:5 x1 2 x2 9 x3 7 x 4 max;
4 x1 2 x2 2 x3 4 x4 6;
i, x {0,1,2}.
i
22
X opt {0,1,2,0};
Fopt 20.
14. САМОСТОЯТЕЛЬНО:
Решить задачу с небулевыми и сбулевыми переменными вида:
7 x1 2 x2 4 x3 5 x 4 max;
4 x 2 x 2 x 4 x 8;
1
2
3
4
i 3, xi {0,1,2},
3 i 4 : xi {0,1}.
15. Часть 4
Принятие решенийна моделях
оптимального
упорядочения
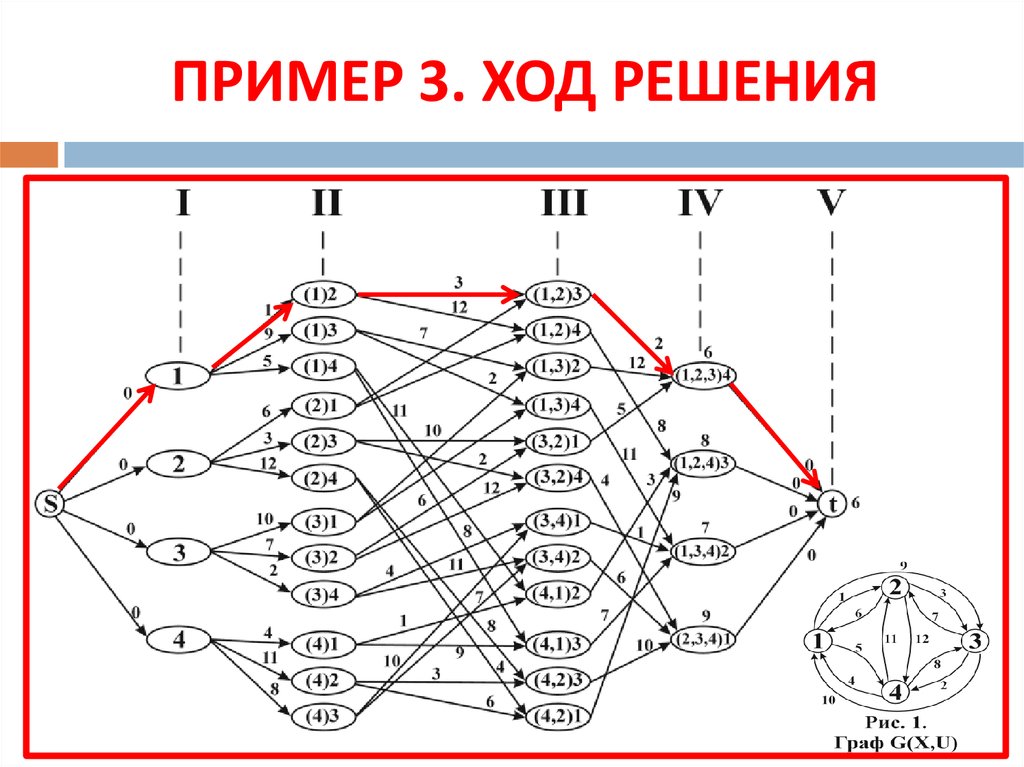
16. ПРИМЕР 3: ЗАДАЧА КОММИВОЯЖЕРА
Решить, пользуясь методом динамическогопрограммирования, разомкнутую задачу
коммивояжера, условия которой отвечают
графу G(X, U), изображенному на рисунке
ниже.
r (i, j ) z (i, j ) min;
i j
xs X : z (i, s ) 0; z ( s, j ) 1;
i
j
xt X : z (i, t ) 1; z (t , j ) 0;
i
j
x X \ ( x x ) : z (i, k ) z (k , j ) 1;
i
j
s
t
k
(i, j ) U : z (i, j ) 1,0.
17. ПРИМЕР 3. ХОД РЕШЕНИЯ
18. Самостоятельно вывести:
Формулы, определяющие:1. Число вершин каждого слоя
построенной сети.
2. Число дуг, заходящих в каждую
вершину i-го слоя.
3. Число дуг, исходящих из каждой
вершины i-го слоя.
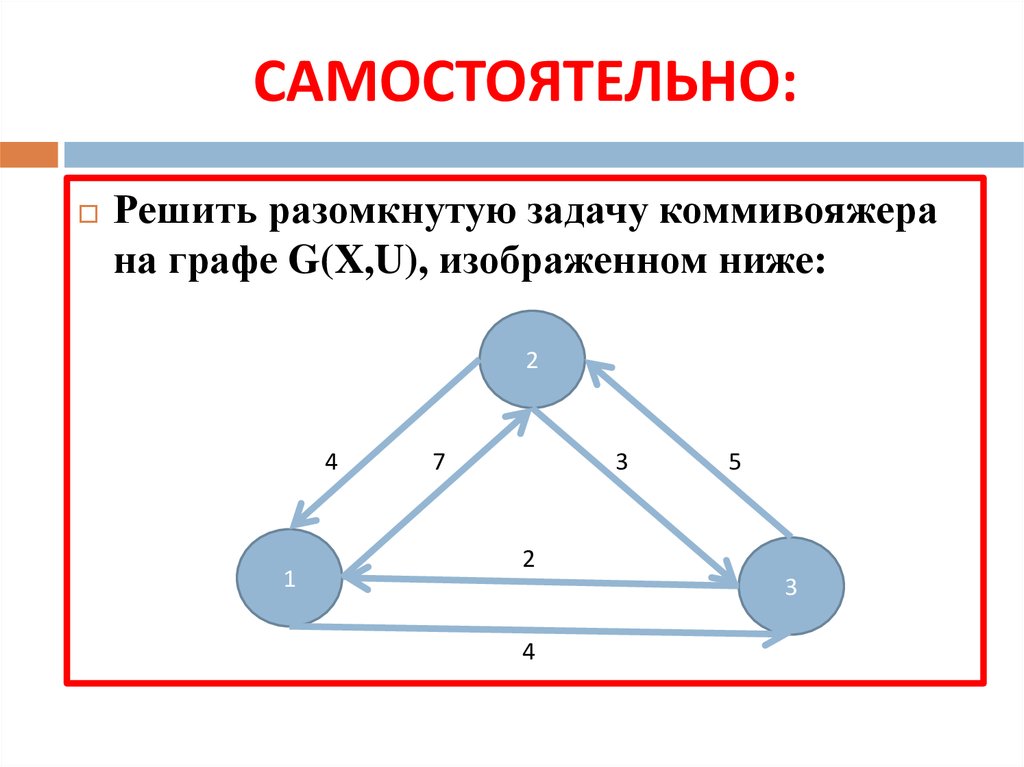
19. САМОСТОЯТЕЛЬНО:
Решить разомкнутую задачу коммивояжерана графе G(X,U), изображенном ниже:
2
4
1
7
3
5
2
3
4














 programming
programming








