Similar presentations:
Квадратные неравенства. Интегрированный урок для учащихся 9 класса
1. Интегрированный урок для учащихся 9 класса по теме «Квадратные неравенства»
Муниципальное бюджетноеобщеобразовательное учреждение
«Гимназия №52» г.Казани
Интегрированный урок
для учащихся 9 класса
по теме «Квадратные неравенства»
Учитель математики Захарова М.А.
Учитель информатики Сырямина И.В.
2. Информационное общество. Информатизация
3. Основные задачи информатизации образования
• повышение качества подготовки специалистов на основеиспользования в учебном процессе современных
информационных технологий;
• применение активных методов обучения и, как результат,
повышение творческой и интеллектуальной составляющих
учебной деятельности;
• интеграция различных видов образовательной деятельности
(учебной, исследовательской и т.д.);
• адаптация информационных технологий обучения к
индивидуальным особенностям обучаемого;
• обеспечение непрерывности и преемственности в обучении;
• разработка информационных технологий дистанционного
обучения;
• совершенствование программно-методического обеспечения
учебного процесса.
4. Персональный компьютер как средства обучения
5. ] отмечаются следующие дидактические возможности компьютера как средства обучения
] отмечаются следующиедидактические возможности
компьютера как средства обучения
• расширенное предъявление учебной
информации;
• индивидуализация процесса обучения;
• усиление мотивации обучения;
• реализация эффективных способов
управления самостоятельной учебной
деятельностью
6. Общее понятие об информационно-коммуникационных технологиях
Общее понятие обинформационнокоммуникационных технологиях
• поддержка и развитие
системности мышления обучаемого;
• поддержка всех видов
познавательной деятельности
обучающегося в приобретении знаний,
развитии и закреплении навыков и умений;
• реализация принципа
индивидуализации учебного процесса при
сохранении его целостности.
7. Образовательные средства ИКТ можно классифицировать по ряду параметров
• 1. По решаемымпедагогическим
задачам
• 2. По функциям в
организации
образовательного
процесса
• 3. По типу
информации:
8.
-средства, обеспечивающие базовую подготовку (электронные учебники, обучающие системы, системы контроля знаний);
средства практической подготовки (задачники, практикумы, виртуальные конструкторы, программы имитационного моделирования, тренажеры);
вспомогательные средства (энциклопедии, словари, хрестоматии, развивающие компьютерные игры, мультимедийные учебные занятия);
комплексные средства (дистанционные учебные курсы).
9. Вопросы
1. Что называется квадратным неравенством содной переменной х?
Ответ
2. При каких условиях квадратный трехчлен
имеет корни, не имеет корней? Приведите
примеры.
Ответ
3. Сформулируйте теорему о решении
квадратных неравенств при Д<0.
Ответ
4. Алгоритм решения квадратного неравенства
Ответ
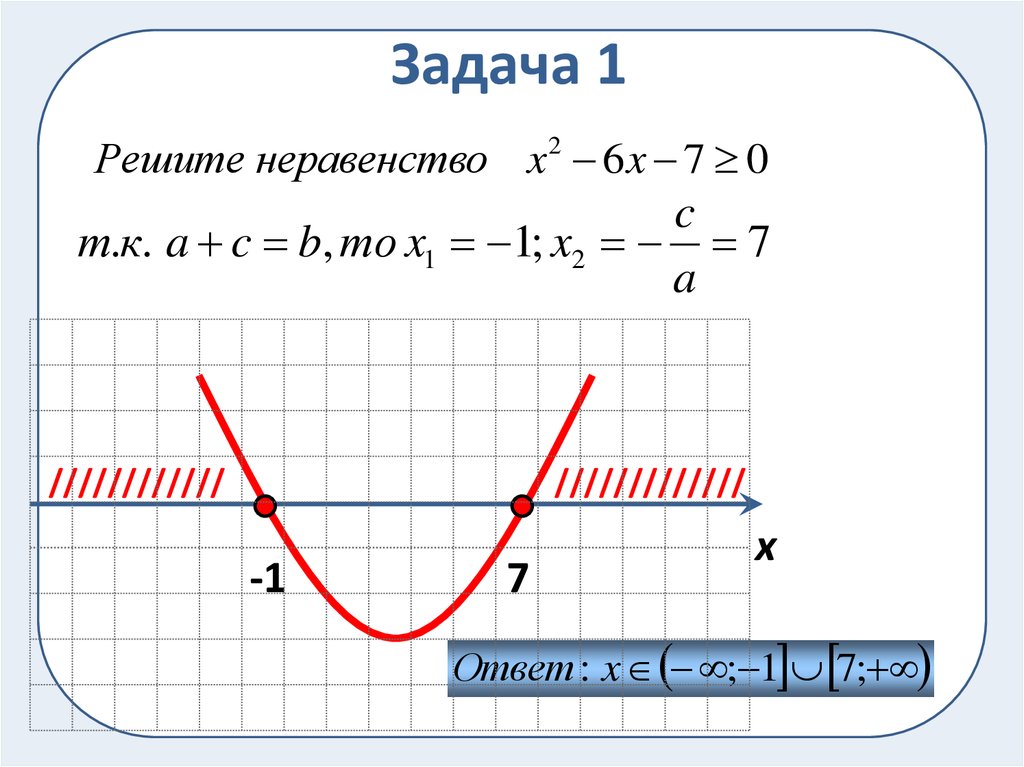
10. Задача 1
Решите неравенство x 2 6 x 7 0c
т.к. a c b, то x1 1; x2 7
a
////////////
/////////////
-1
7
x
Ответ : x ; 1 7;
11. Задача 2
Решите неравенство x 6 x 5 02
т.к. a c b 0, то x1 1; x 2
/////////////
1
b
a
5
1
5
/////////////////
5
x
Ответ : x ;1 5;
12. Задача 3
Решите неравенство x 4 x 4 02
b 4
D 0; x
2
2a 2
x
2
Ответ : {2}.
13. Задача №14
Решите неравенство x 4 x 2 02
14. Задача №10(в)
Найдите область определения выражения f ( x)7
f ( x)
14 2 x 2 3 x
15. Квадратное неравенство с параметром
При каких значениях m неравенствоmx (2 m) 3 2m 0
2
выполняется только для одного
действительного значения x?
Решение:
1. m=0
Имеем 2 x 3 0 x 1,5 m 0 не подходит.
16. Квадратное неравенство с параметром
2. m≠0Рассмотрим квадратичную функцию
y mx (2 m) 3 2m
2
• если т<0, то ветви параболы направлены в
низ, и очевидно исходное неравенство не
может иметь единственное решение.
• если m>0, то возможны три случая
17.
• Д=0m 0
2
(
m
2
)
4m(3 2m) 0
m 4m 4 12m 8m 0
9m 2 16m 4 0
2
2
D1 64 36 28 (2 7 ) 2
8 2 7
m1
, где m 0
9
8 2 7
m2
, где m 0
9
8 2 7
8 2 7
Ответ : m
или m
.
9
9
18. Самостоятельная работа
• Задания №1-3 - решить неравенство.• Задание №4 - найти область определения
выражения.
19. Домашнее задание
Решить:• №8(а,б),
• №10(б),
• №14(а,б),
• №15(а),
• №18(дополнительно).
• Cоставить блок-схему к программе решения
квадратного неравенства
20. Ответ:
Неравенство вида ax2+bx+с>0(<0),где a,b,c -действительные числа и а≠0
называется квадратным неравенством.
Например: 2х2-3х+4<0, х2-3>0.
21. Ответ:
Квадратный трехчлен имеет два корня приД>0, квадратный трехчлен имеет один
корень при Д=0, квадратный трехчлен не
имеет корней при Д<0.
Например:
• х2-2х+4, не имеет корней , т.к. Д=-12<0;
• х2-2х+1, имеет один корень, т.к. Д=0;
• х2-2х-1 имеет два корня, т.к. Д>0.
22. Ответ:
Квадратный трехчлен ax2 + bx + cс отрицательным дискриминантом при всех
значениях х имеет знак старшего
коэффициента a.
23.
Алгоритм решения квадратного неравенстваВид
неравенства
ax2 + bx + c >0
ax2 + bx + c ≥ 0
ax2 + bx + c < 0
ax2 + bx + c ≤ 0
Д>0 a>0
(- ;x1)U(x2;+ )
(- ;x1]U[x2;+ )
(x1;x2)
[x1;x2]
(x1;x2)
[x1;x2]
(- ;x1)U(x2;+ )
(- ;x1]U[x2;+ )
Д=0 a>0
(- ;x)U(x;+ )
(- ;+ )
Нет решения
{x}
a<0
Нет решения
{x}
(- ;x)U(x;+ )
(- ;+ )
(- ;+ )
(- ;+ )
Нет решения
Нет решения
Нет решения
Нет решения
(- ;+ )
(- ;+ )
a<0
Д<0 a>0
a<0
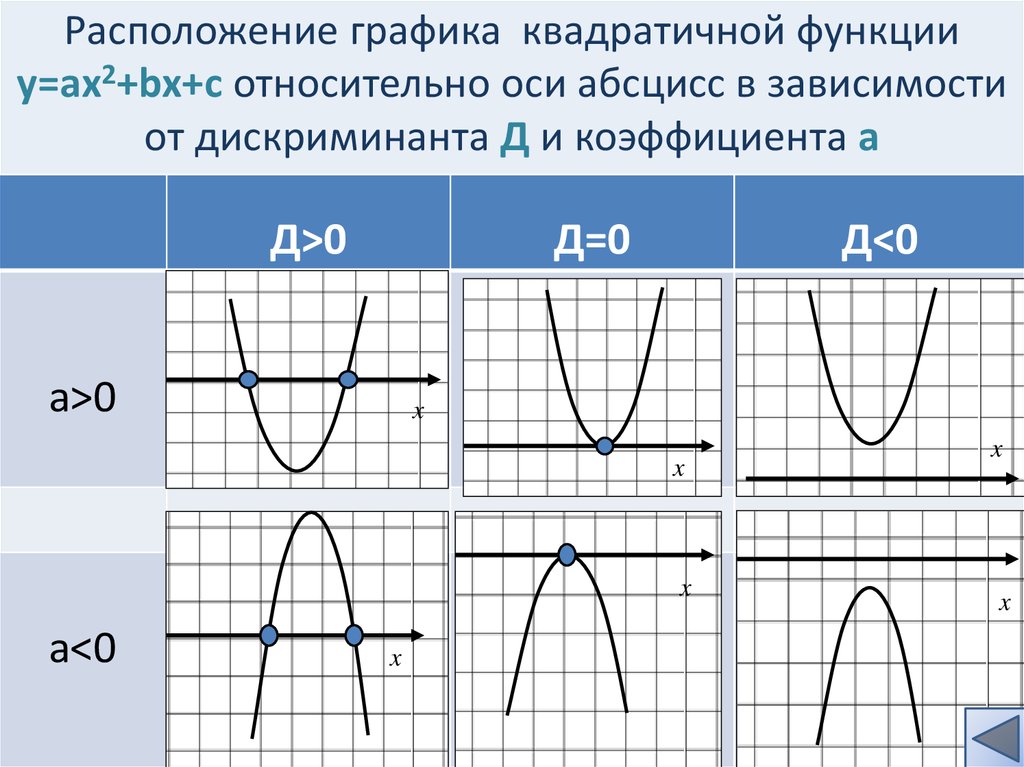
24. Расположение графика квадратичной функции у=aх2+bx+c относительно оси абсцисс в зависимости от дискриминанта Д и коэффициента а
Д>0Д=0
a>0
Д<0
x
x
x
a<0
x
x
x
25.
Условный операторif <условие> then begin
{что делать, если условие верно}
end
else begin
{что делать, если условие неверно}
end;




![] отмечаются следующие дидактические возможности компьютера как средства обучения ] отмечаются следующие дидактические возможности компьютера как средства обучения](https://cf2.ppt-online.org/files2/slide/x/XWMctFQCOD6x3uaPI7ymK8Th0r1bkvBdSRnYLJ59p/slide-4.jpg)


















 mathematics
mathematics








