Построение графика квадратичной функции

1. Построение графика квадратичной функции.

Муниципальное автономное общеобразовательное учреждение
«Лицей №1»
Построение графика
квадратичной
функции.
Нагаева Светлана Николаевна
учитель математики
г.Березники, 2013г.

2. Тип и цели урока

урок изучения нового материала.
активизировать сознательную деятельность
учащихся;
научить строить график функции у = ах² + вх + с,
читать его и использовать приобретенные
знания.
С.Н.Нагаева
2

3. Применение изучаемого материала на практике

у = ах² + вх + с – квадратичная функция.
график функции – парабола, ветви которой
направлены вверх, если а > 0 и вниз, если а < 0.
С параболой можно встретиться во многих
областях знания.
Примеры:
отражающая поверхность фары в автомобиле
имеет параболическую форму.
С.Н.Нагаева
3

4. Применение изучаемого материала на практике

в межпланетном пространстве многие кометы
движутся по параболам (вблизи Солнца).
парабола применяется в строительном деле.
С.Н.Нагаева
4

5. Применение изучаемого материала на практике

Зависимость площади квадрата от длины его
стороны описывается квадратичной функцией.
S – площадь квадрата,
S = а²
а – его сторона.
С.Н.Нагаева
5

6. Алгоритм построения параболы у = ах² + вх + с

1. Вычислить координаты пяти точек В, А, А1,
Х1, Х2 с помощью формулы функции
у=ах²+вх+с.
1.1. В – вершина параболы, ее абсцисса
хв=-в/2а,
ее ордината
ув=а(-в/2а)²+в(-в/2а)+с.
1.2. А - точка пересечения параболы с
осью ОY, ее абсцисса хА=0,
ее ордината уА=а∙0²+в∙0+с,
А(0;с).
С.Н.Нагаева
6

7. Алгоритм построения параболы у = ах² + вх + с

2. Построить график квадратичной функции.
2.1. Изобразить координатную плоскость;
2.2. Изобразить точки В, А, А1, Х1, Х2;
2.3. Провести параболу через эти точки.
С.Н.Нагаева
7

8. Пример

Построить график квадратичной функции
у = х²-2х-3
Построение:
1. хв=-(-2)/(2∙1)=1; ув=1²-2∙1-3=-4.
2. хА=0; уА=-3.
3. хА1=-(-2)/1=2;
уА1=-3.
4. х²-2х-3=0, D=(-2)²+12=16>0 => 2 действ. корня,
5. х1=(2-√16)/(2∙1)=-1, х2=(2+√16)/(2∙1)=3.
6. В(1;-4), А(0;-3), А1(2;-3), Х1(-1;0), Х2(3;0).
С.Н.Нагаева
8

9. Расположение параболы на координатной плоскости в зависимости от знаков коэффициента а и дискриминанта D

С.Н.Нагаева
9

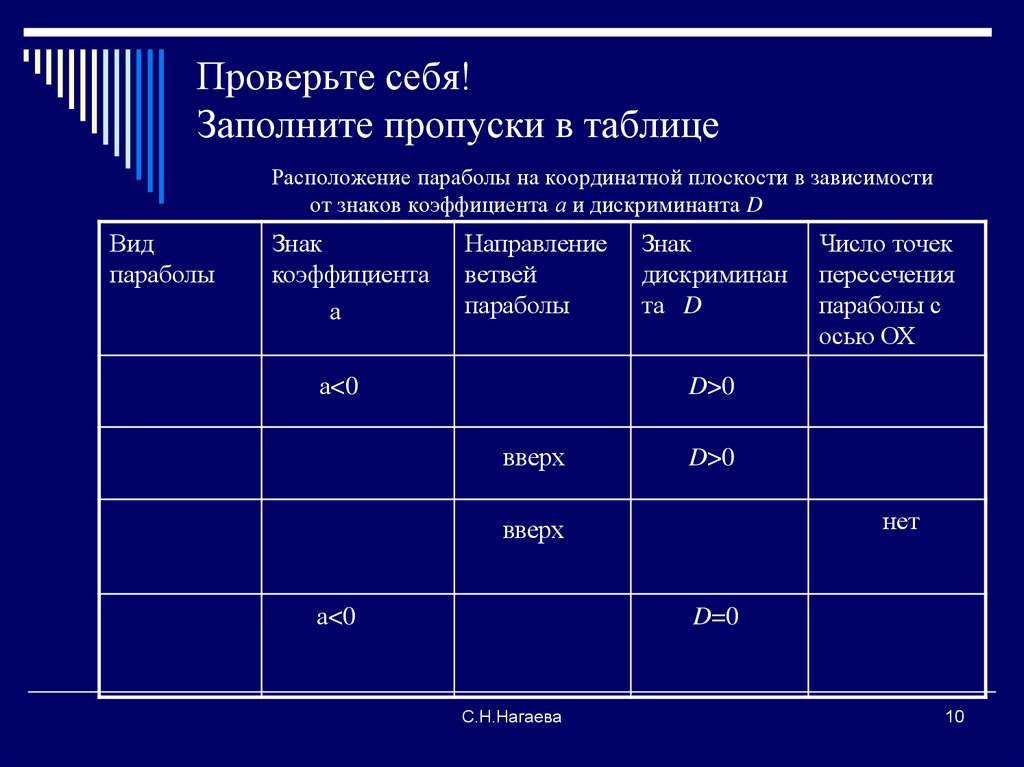
10. Проверьте себя! Заполните пропуски в таблице

Расположение параболы на координатной плоскости в зависимости
от знаков коэффициента а и дискриминанта D
Вид
параболы
Знак
коэффициента
а
Направление
ветвей
параболы
а<0
Знак
дискриминан
та D
Число точек
пересечения
параболы с
осью ОХ
D>0
вверх
D>0
нет
вверх
а<0
D=0
С.Н.Нагаева
10

11. Подведение итогов урока

Домашнее задание:
1.Задание с продолжением.
а) Запишите функцию, графиком которой является
парабола,
б) и ее ветви опущены вниз,
в) и она проходит через точку (-1;-8).
2. Постройте график квадратичной функции,
если известно, что он проходит через точки
(-4;4), (-2;-3), (0;4).
С.Н.Нагаева
11