Similar presentations:
Алгоритм построения графика квадратичной функции
1. МОУ Молоковская СОШ
Унанян С. Н.2. Алгоритм построения графика квадратичной функции
у = ах²+вх+с – функцияквадратичная, график - парабола
3. 1)направление «ветвей» параболы
если а>0, то «ветви»
параболы
направлены вверх;
• если а<0, то «ветви»
параболы направлены
вниз;
• У = х² - 6х + 5,
• а = 1 > 0 - «ветви»
параболы направлены
вверх;
4. 2)Нахождение координат вершины
• Х0= -,
• У = х² - 6х + 5,
• У0=у(х0),
• Х0= -
• (Х0 ; У0 );
• У0=у(х0)= 9 – 18 + 5 = - 4
• (3; - 4)
=3,
5. 3)Ось симметрии параболы
• Ось симметриипараболы – прямая,
параллельная оси
ординат и проходящая
через вершину
параболы;
• Х = Х0.
• Координаты вершины
параболы (3; - 4),
• Ось симметрии
параболы Х = 3.
6. 4) точки пересечения параболы с осью абсцисс У = 0
• ах²+вх+с = 0• х² - 6х + 5 = 0,
• х1 = 5, х2 = 1,
• Координаты точек
пересечения:
(х1;0), (х2;0).
• (5; 0), (1; 0).
7. 5) Точки пересечения параболы с осью ординат Х = 0
• Парабола пересекаетось ординат в точке с
координатами (0; С)
• С =5
• Парабола пересекает
ось ординат в точке с
координатами (0;5)
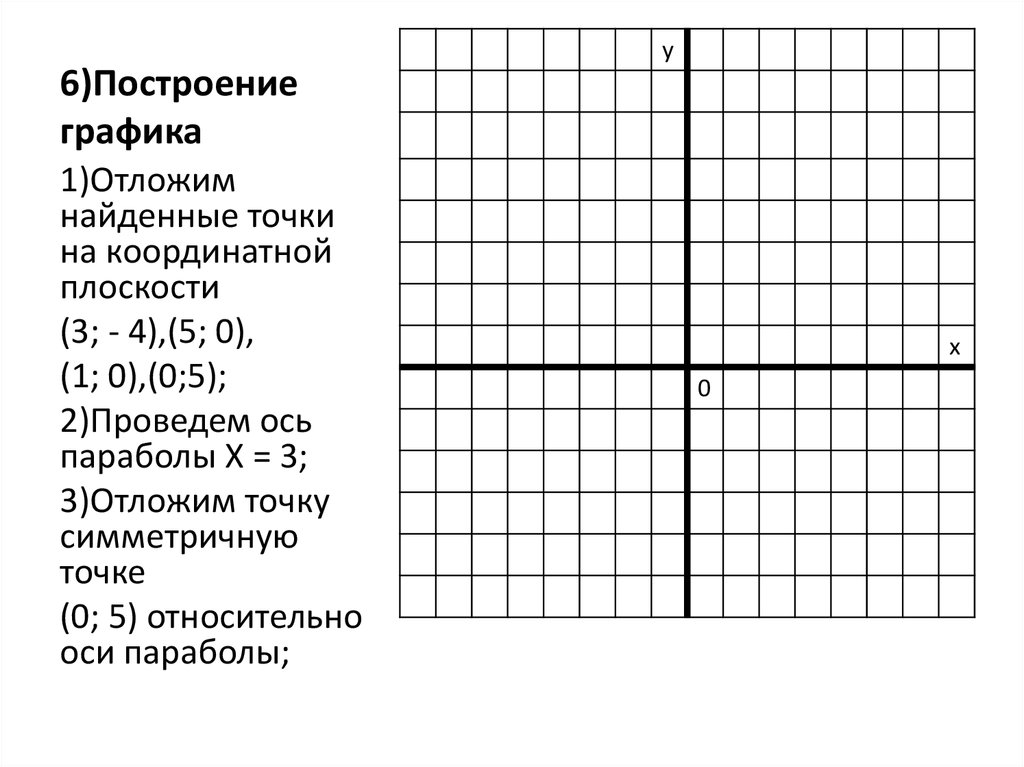
8. 6)Построение графика
у6)Построение
графика
1)Отложим
найденные точки
на координатной
плоскости
(3; - 4),(5; 0),
(1; 0),(0;5);
2)Проведем ось
параболы Х = 3;
3)Отложим точку
симметричную
точке
(0; 5) относительно
оси параболы;
х
0
9.
y4) Соединим
получившиеся точки
0
x







 mathematics
mathematics








