Similar presentations:
Тренировочная работа № 30
1.
2.
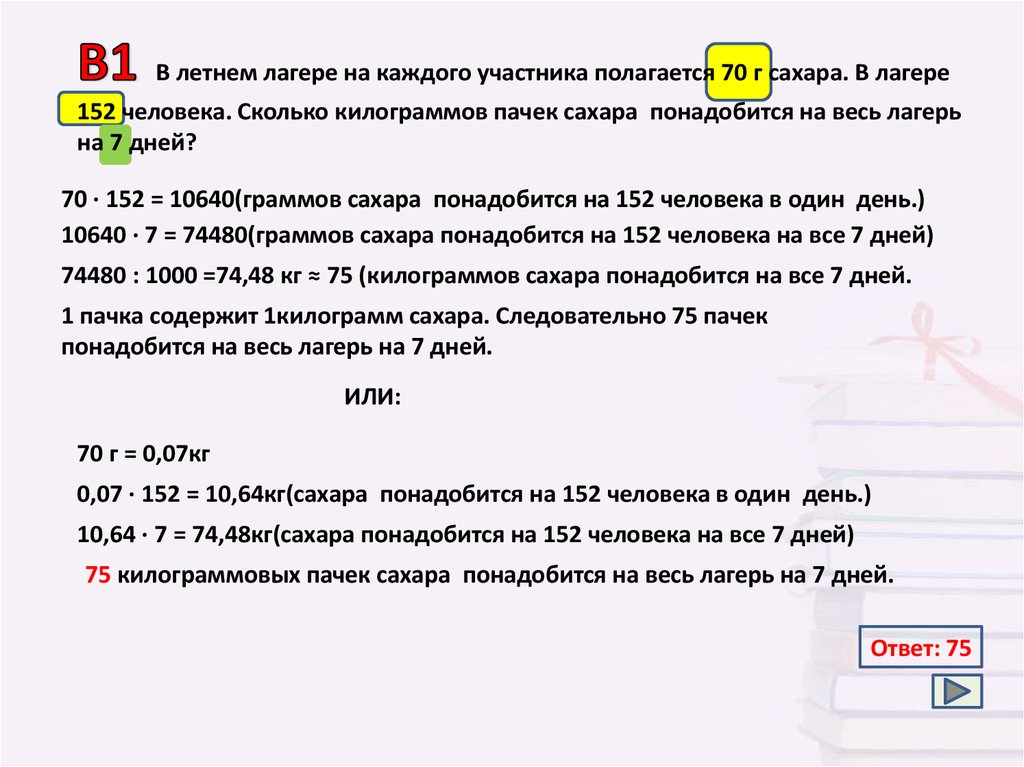
В летнем лагере на каждого участника полагается 70 г сахара. В лагере152 человека. Сколько килограммов пачек сахара понадобится на весь лагерь
на 7 дней?
70 · 152 = 10640(граммов сахара понадобится на 152 человека в один день.)
10640 · 7 = 74480(граммов сахара понадобится на 152 человека на все 7 дней)
74480 : 1000 =74,48 кг ≈ 75 (килограммов сахара понадобится на все 7 дней.
1 пачка содержит 1килограмм сахара. Следовательно 75 пачек
понадобится на весь лагерь на 7 дней.
ИЛИ:
70 г = 0,07кг
0,07 · 152 = 10,64кг(сахара понадобится на 152 человека в один день.)
10,64 · 7 = 74,48кг(сахара понадобится на 152 человека на все 7 дней)
75 килограммовых пачек сахара понадобится на весь лагерь на 7 дней.
Ответ: 75
3.
На диаграмме показана среднемесячная температуравоздуха в Симферополе за каждый месяц 1988 года. По
горизонтали указываются месяцы, по вертикали - температура в
градусах Цельсия. Определите по диаграмме, в каком месяце
произошел самый большой перепад средней температуры по
сравнению с предыдущим месяцем. В ответе напишите номер
месяца.
8о
Ответ: 11
4.
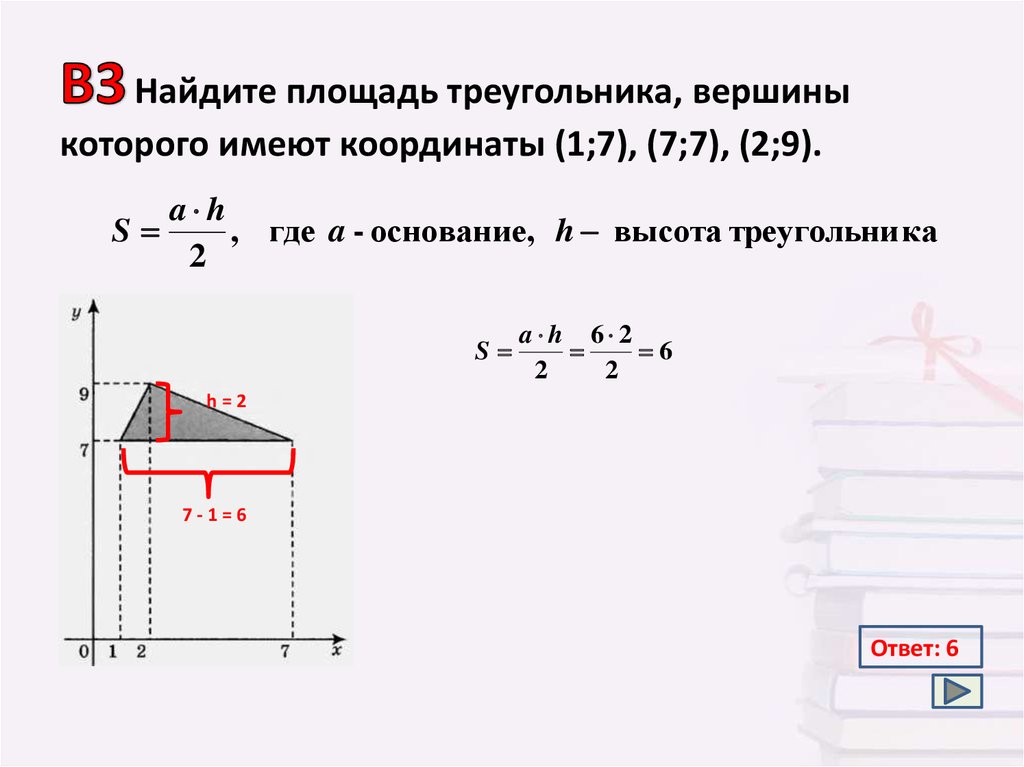
Найдите площадь треугольника, вершиныкоторого имеют координаты (1;7), (7;7), (2;9).
a h
S
, где a - основание, h высота треугольни ка
2
S
a h 6 2
6
2
2
h=2
7-1=6
Ответ: 6
5.
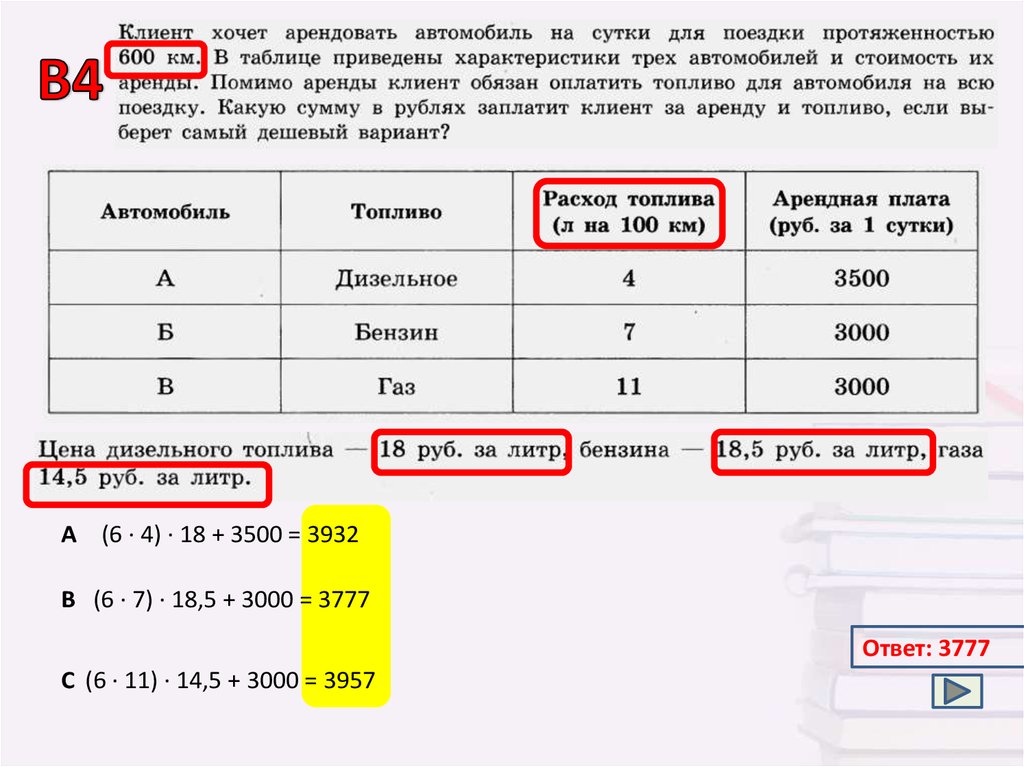
A (6 · 4) · 18 + 3500 = 3932B (6 · 7) · 18,5 + 3000 = 3777
Ответ: 3777
C (6 · 11) · 14,5 + 3000 = 3957
6.
Найти корень уравнения2х 37 (7)
2
2х 37 7
2
2х 37 49;
2х 49 37;
2х 12;
х 6.
Ответ: 6
7.
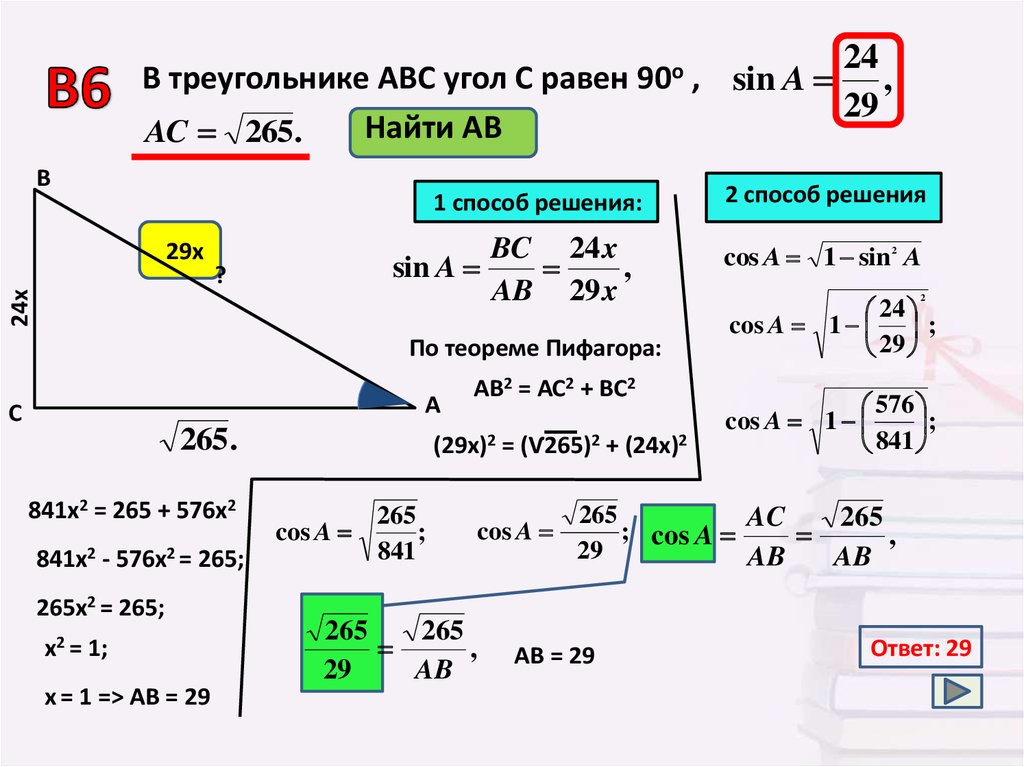
24В треугольнике АВС угол С равен 90о , sin A ,
29
Найти АВ
AC 265.
В
1 способ решения:
24х
29х
BC 24 x
sin A
,
AB 29 x
?
По теореме Пифагора:
А
С
265 .
841х2 = 265 + 576х2
841х2 - 576х2 = 265;
265х2 = 265;
х2 = 1;
х = 1 => АВ = 29
АВ2 = АС2 + ВС2
(29х)2 = (Ѵ265)2 + (24х)2
cos A
265
;
841
265
265
,
29
AB
cos A
2 способ решения
cos A 1 sin A
2
24
cos A 1 ;
29
2
576
cos A 1
;
841
265
AC
265
; cos A
,
29
AB
AB
АВ = 29
Ответ: 29
8.
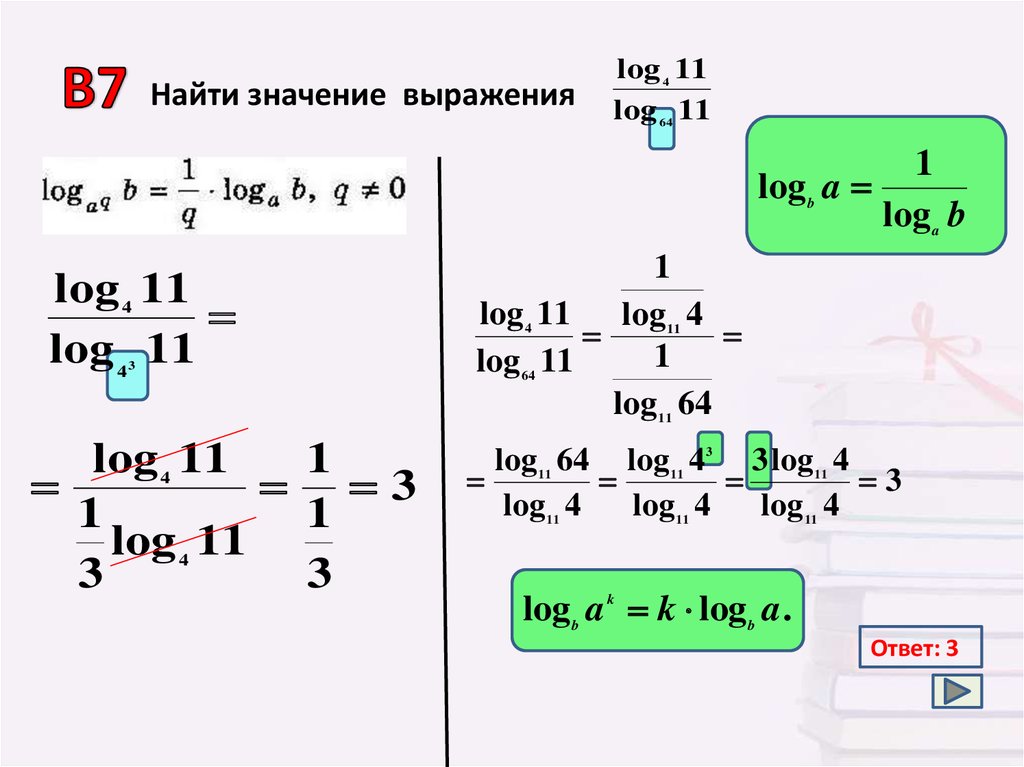
Найти значение выраженияlog 11
log 11
4
64
1
log a
log b
b
a
log 11
log 11
4
43
1
log 11
log 4
1
log 11
log 64
4
11
64
11
log 11
1
3
1
1
log 11
3
3
4
3
log 64 log 4 3 log 4
3
log 4
log 4
log 4
11
11
11
11
11
11
4
log a k log a .
k
b
b
Ответ: 3
9.
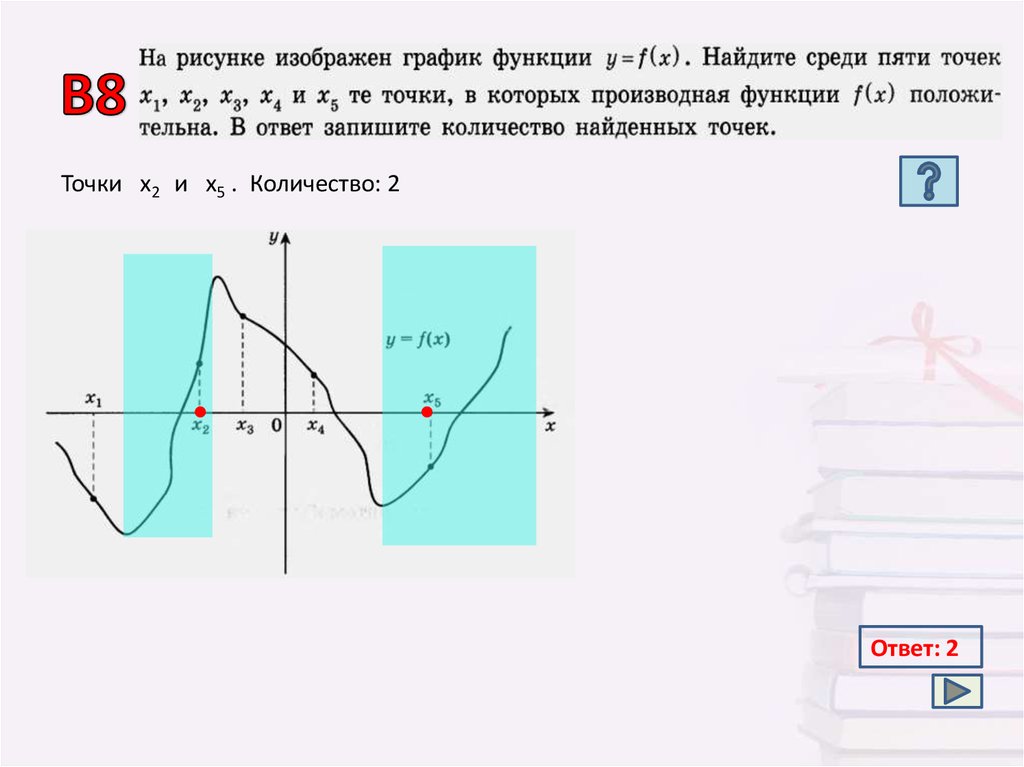
Точки х2 и х5 . Количество: 2Ответ: 2
10.
Теоретические сведенияЕсли функция у = f (х) определена и непрерывна в некотором промежутке и во
всех внутренних точках этого промежутка имеет неотрицательную производную
(f ʹ (х) ≥ 0), причем равенство f ʹ (х) = 0 выполняется не более чем в конечном числе
точек этого промежутка, тогда функция у = f (х) возрастает на этом промежутке.
И ТАК: Решим эту задачу, воспользовавшись следующим утверждением.
Производная непрерывно дифференцируемой функции на
промежутке возрастания не отрицательна. Значит
необходимо выделить промежутки возрастания функции и
сосчитать количество целых чисел, принадлежащих этим
промежуткам. Причем производная равна нулю на концах
этих промежутков, значит, нужно брать только внутренние
точки промежутков.
11.
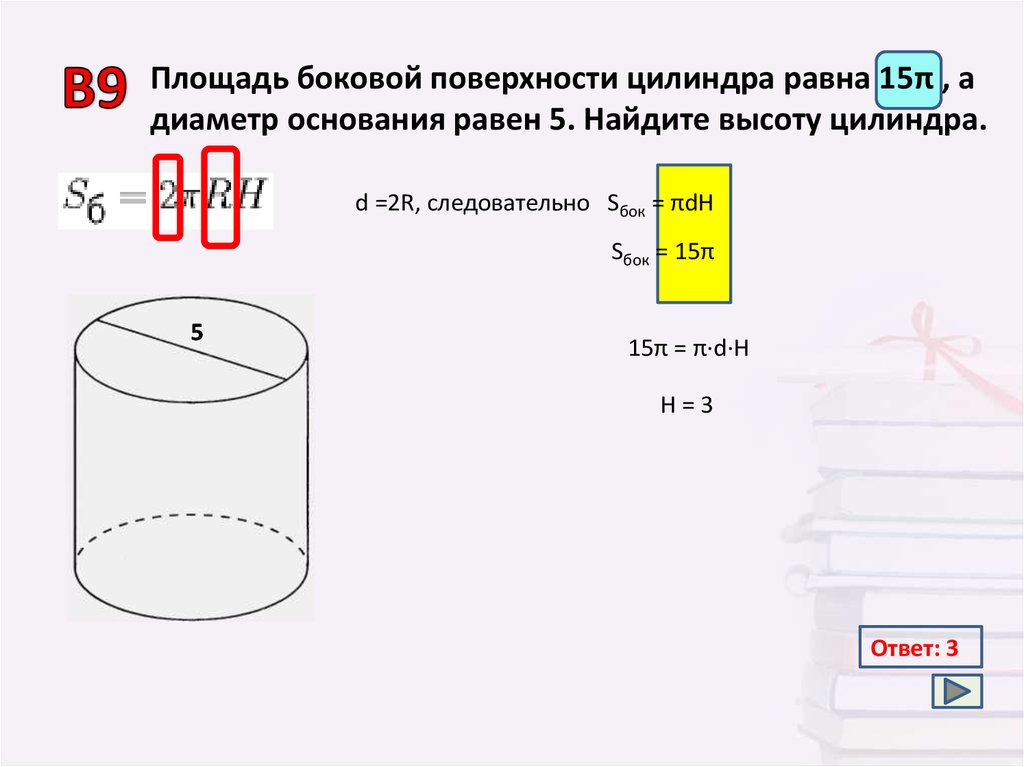
Площадь боковой поверхности цилиндра равна 15π , адиаметр основания равен 5. Найдите высоту цилиндра.
d =2R, следовательно Sбок = πdH
Sбок = 15π
5
15π = π·d·H
H=3
Ответ: 3
12.
Родительский комитет закупил 40 пазлов для подарковдетям на окончание учебного года, из них 14 с видом
природы и 26 с историческими достопримечательностями. Подарки распределяются случайным образом.
Найдите вероятность того, что Вове достанется пазл с
видом природы.
Число благоприятных исходов – это 14 (пазлы с видом природы)
Число всех возможных исходов – это 40 (все пазлы для подарков)
Найдем отношение благоприятных исходов эксперимента 14
к числу всех возможных исходов 40
14
0,35
40
Ответ: 0,35
13.
В основании прямой призмы лежит квадрат со стороной3. Боковые ребра равны 4 . Найдите объем цилиндра,
описанного около этой призмы.
3
3
R
Диагональ квадрата можно найти по теореме Пифагора:
d 3 3 27 3 2
2
4
2
d 3 2
2
2
Найдем площадь основания цилиндра
R
Sоснов = π·R2
3 2
;
S
2
2
3
3
осн
R
R
h
S
осн
9 2
4,5
4
4
V 4,5
Ответ: 18
4
18
14.
U =220 BI ≤ 11 A
R-?
I
U
U
I;
R
R
220
11;
R
220
R;
11
20
R 20.
R = 20
Ответ: 20
15.
Первая труба пропускает на 3 л воды в минуту меньше, чем вторая.Сколько литров воды в минуту пропускает вторая труба, если резервуар
объемом 648 л она заполняет на 3 минуты быстрее, чем первая труба?
Пусть х литров воды в минуту пропускает вторая труба, тогда
(х – 3) литров воды в минуту пропускает первая труба.
648
время, за которое резервуар объемом 648 л заполняет вторая труба.
x
648
время, за которое резервуар объемом 648 л заполняет первая труба.
x 3
648
648
3
;
x
x 3
648( x 3) 3( x 3 x ) 648 x;
2
648 x 3 648 3 x 9 x 648 x;
2
3 x 9 x 3 648 0;
2
x 3 x 648 0;
2
:3
648 x 3 648 3 x 9 x 648 x;
2
x 27;
x 24( постор .корень)
Ответ: 27
16.
Найдите наибольшее значение функцииу ln( x 6) 9 x на отрезке - 5,5; 0 .
9
ОДЗ: х + 6 > 0 => х > -6. Отрезок [-5,5; 0] принадлежит области допустимых значений
Используем свойство логарифмов:
у 9 ln( x 6) 9 x
-6
х
-5,5
0
Производная натурального логарифма определяется так:
( x 6)
1
9;
y 9
9;
x 6
x 6
9 9 x 54
45 9 x
y 0;
y
; y
;
x 6
x 6
y 9
х +6 = 0
9 x 45;
45 9 x 0;
y( 5) ln( 5 6) 9 ( 5);
9
x 5;
y( 5) 0 45 45.
y( 5,5) ln( 5,5 6) 9 ( 5,5);
y( 5,5) 9 ln(0,5) 49,5.
y(0) ln(0 6) 9 0;
y(0) 9 ln 6.
9
9
Ответ: 45










 mathematics
mathematics