Урок 30. Линейная функция у = кх

1.

2.

№ 9.3(а,б)
у = kх
у = kх
12 = k · 3
– 25 = k · 5
k=4
k=–5
возрастает
убывает

3.

№ 9.4(а,б)
х
у
у = 4х
у
у = kх
48 = k · 12
k=4
1
0
1
х

4.

№ 9.4(а,б)
х
у
у = – 2х
у
у = kх
32 = k · (- 16)
32 = – 16k
16k = – 32
k=–2
1
0 1
х

5.

№ 9.5
точка В лежит во II координатном углу
Ответ: у = – 4х

6.

№ 9.7
А(0; 0)
В(2; – 4)
у = – 2х
у = – 2х
0=–2·0
0 = 0 верно
принадлежит
графику
–4=–2·2
– 4 = – 4 верно
принадлежит
графику

7.

№ 9.7
С(5; 3)
D(– 4; 8)
у = – 2х
у = – 2х
3=–2·5
3 = – 10 неверно
не принадлежит
графику
Ответ: А, В и D
8 = – 2 · (– 4)
8 = 8 верно
принадлежит
графику

8.

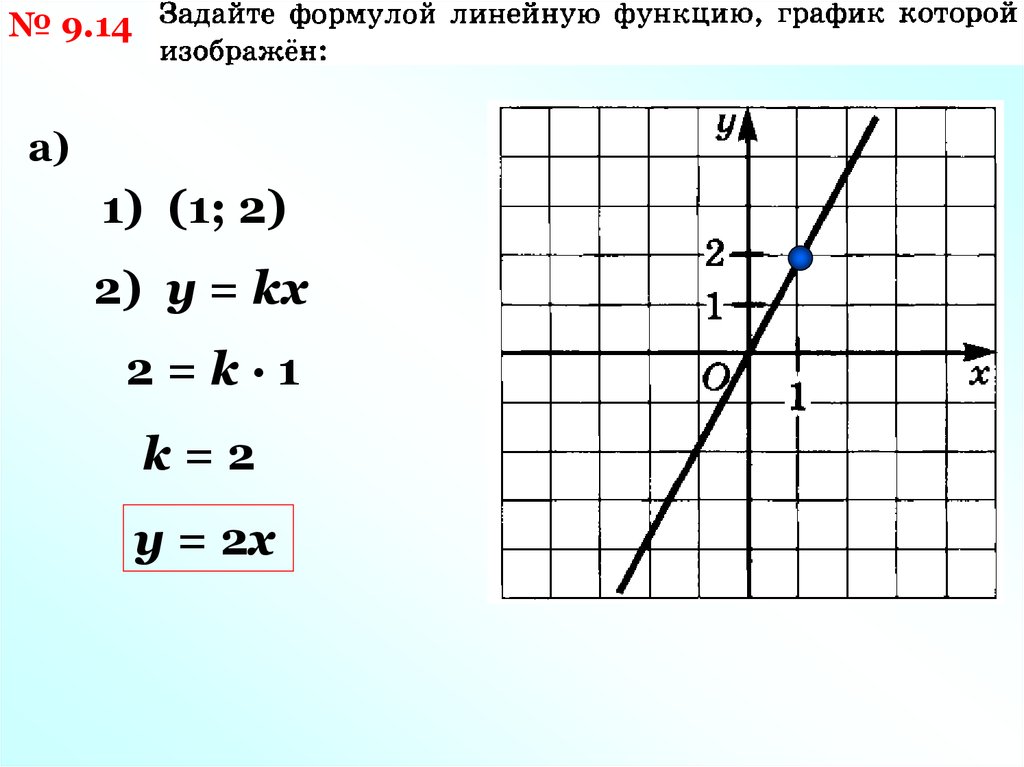
№ 9.14
а)
1) (1; 2)
2) у = kх
2=k·1
k=2
у = 2х

9.

№ 9.14
б) 1) (3; – 3)
2) у = kх
–3=k·3
k=–3:3
k=–1
у=–х

10.

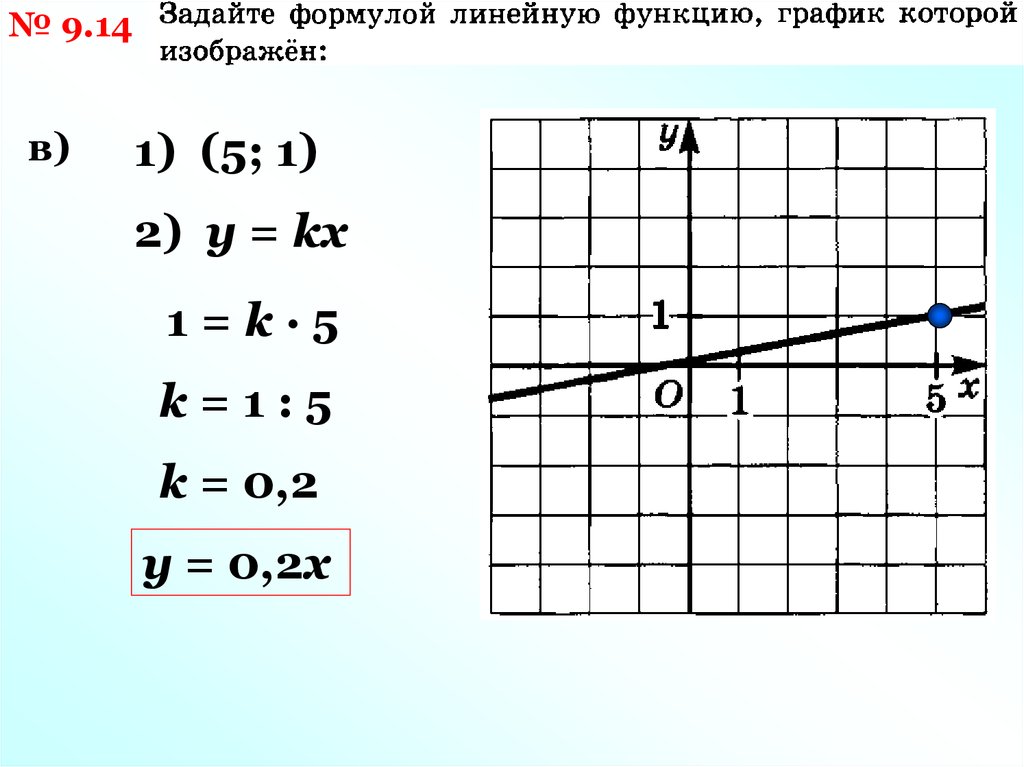
№ 9.14
в)
1) (5; 1)
2) у = kх
1=k·5
k=1:5
k = 0,2
у = 0,2х

11.

№ 9.14
г)
1) (1; – 3)
2) у = kх
–3=k·1
k=–3
у = – 3х

12.

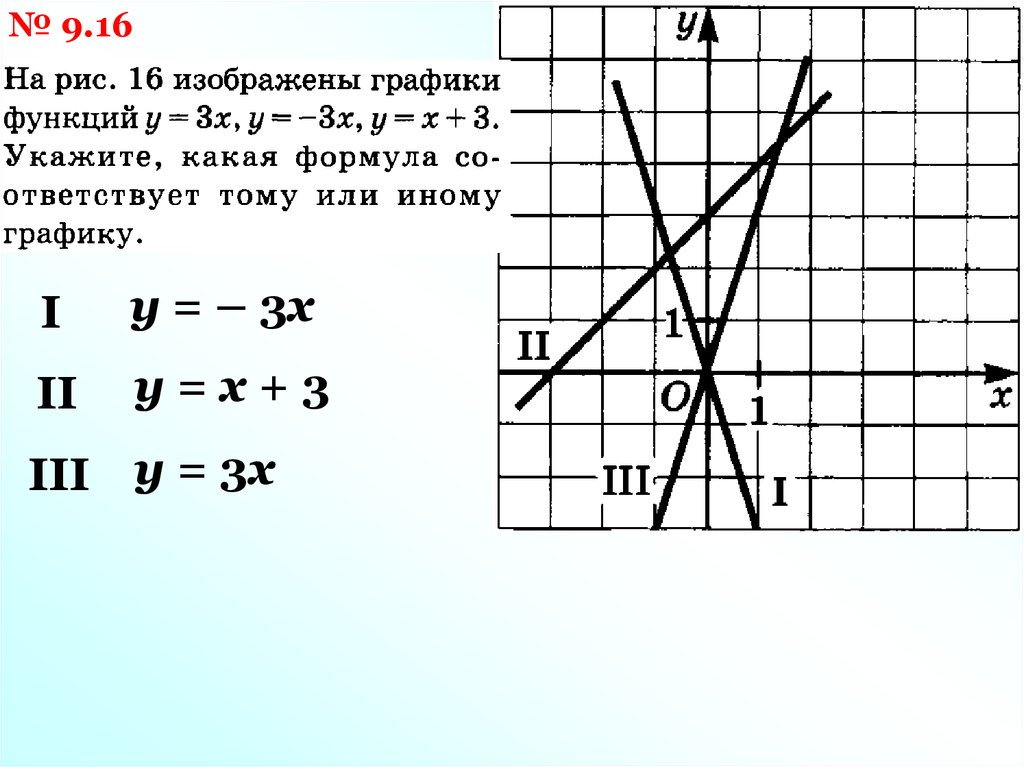
№ 9.16
I
у = – 3х
II
у=х+3
III у = 3х

13.

30.10.2019
Классная
р а б о т а.
Линейная фукция у = kx.

14.

№ 9.15
а)
y = kx + m
k>0
m>0

15.

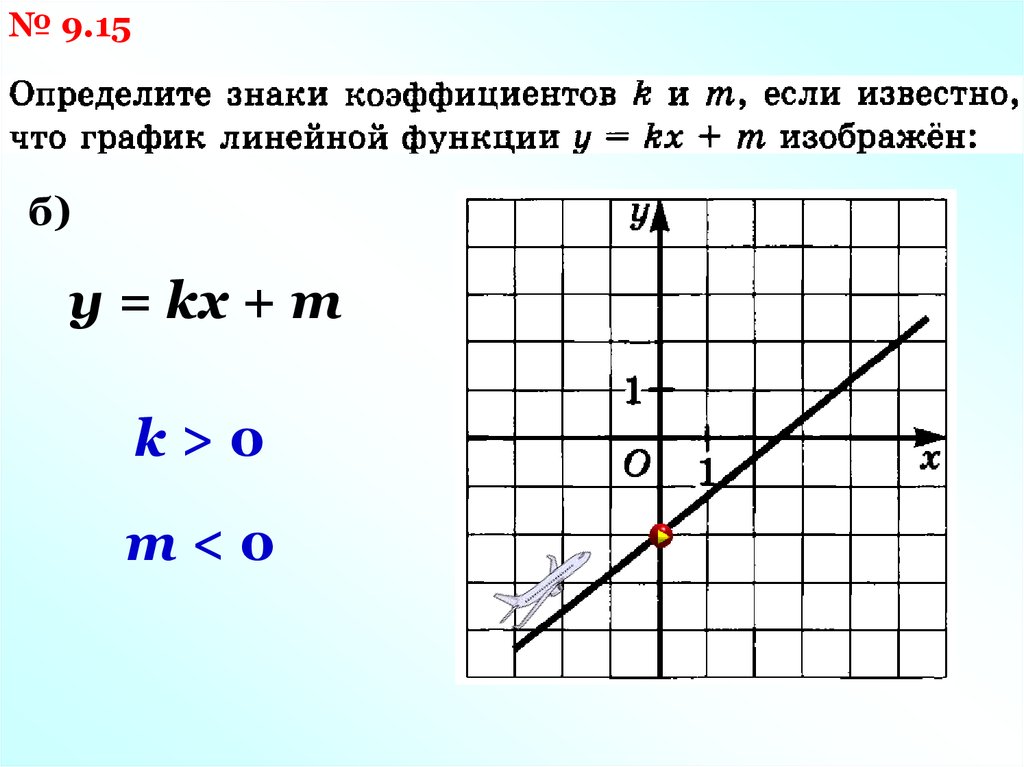
№ 9.15
б)
y = kx + m
k>0
m<0

16.

№ 9.15
в)
y = kx + m
k<0
m>0

17.

№ 9.15
г)
y = kx + m
k<0
m<0

18.

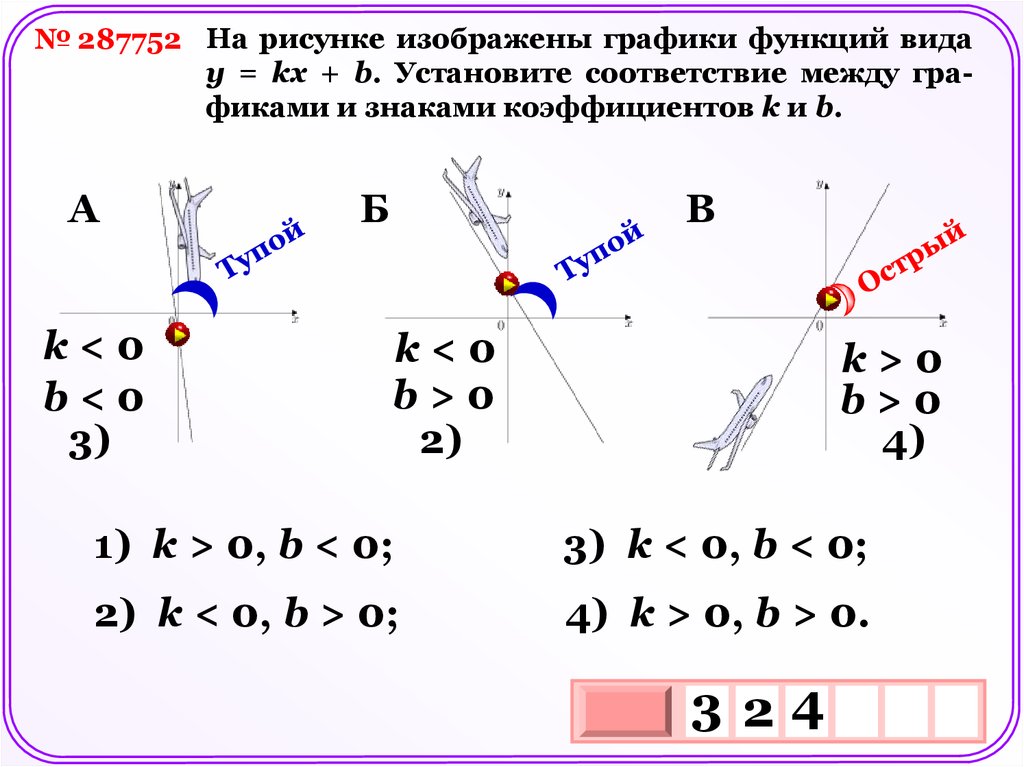
№ 287752 На рисунке изображены графики функций вида
у = kх + b. Установите соответствие между графиками и знаками коэффициентов k и b.
А
k<0
b<0
3)
Б
В
k<0
b>0
2)
k>0
b>0
4)
1) k > 0, b < 0;
3) k < 0, b < 0;
2) k < 0, b > 0;
4) k > 0, b > 0.
324
3
10 х
х

19.

№ 287753 На рисунке изображены графики функций вида
у = kх + b. Установите соответствие между графиками и знаками коэффициентов k и b.
А) k < 0, b < 0; Б) k > 0, b > 0; В) k < 0, b > 0.
1)
2)
k>0
b<0
3)
k>0
b>0
Б)
k<0
b>0
В)
4)
k<0
b<0
А)
423
3
10 х
х

20.

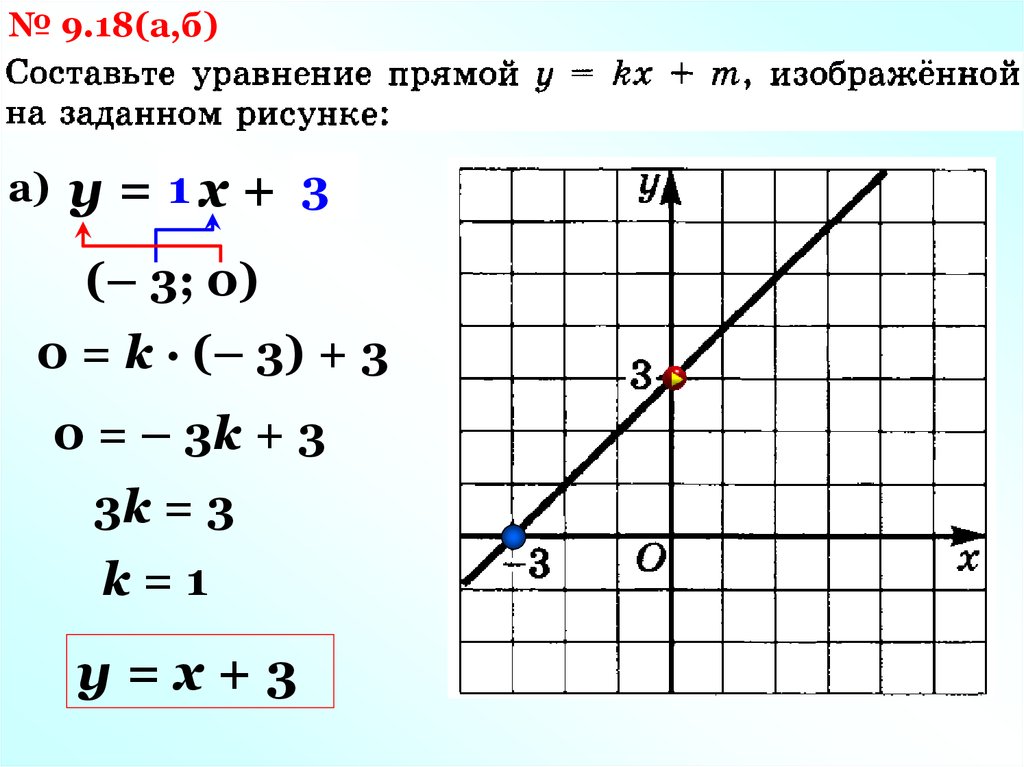
№ 9.18(а,б)
а)
3
1 +m
y = kx
(– 3; 0)
0 = k · (– 3) + 3
0 = – 3k + 3
3k = 3
k=1
y=x+3

21.

№ 9.18(а,б)
б)
2 +
–m
1
y = kx
(2; 3)
3=k·2–1
3 = 2k – 1
– 2k = – 1 – 3
– 2k = – 4
k=2
y = 2x – 1

22.

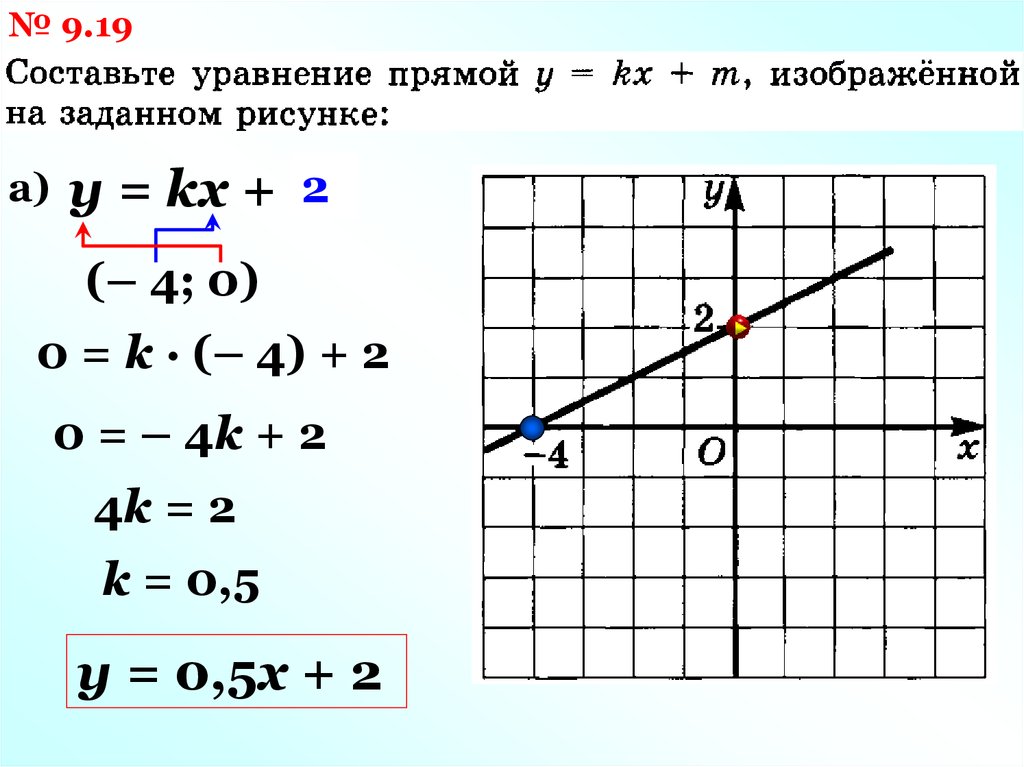
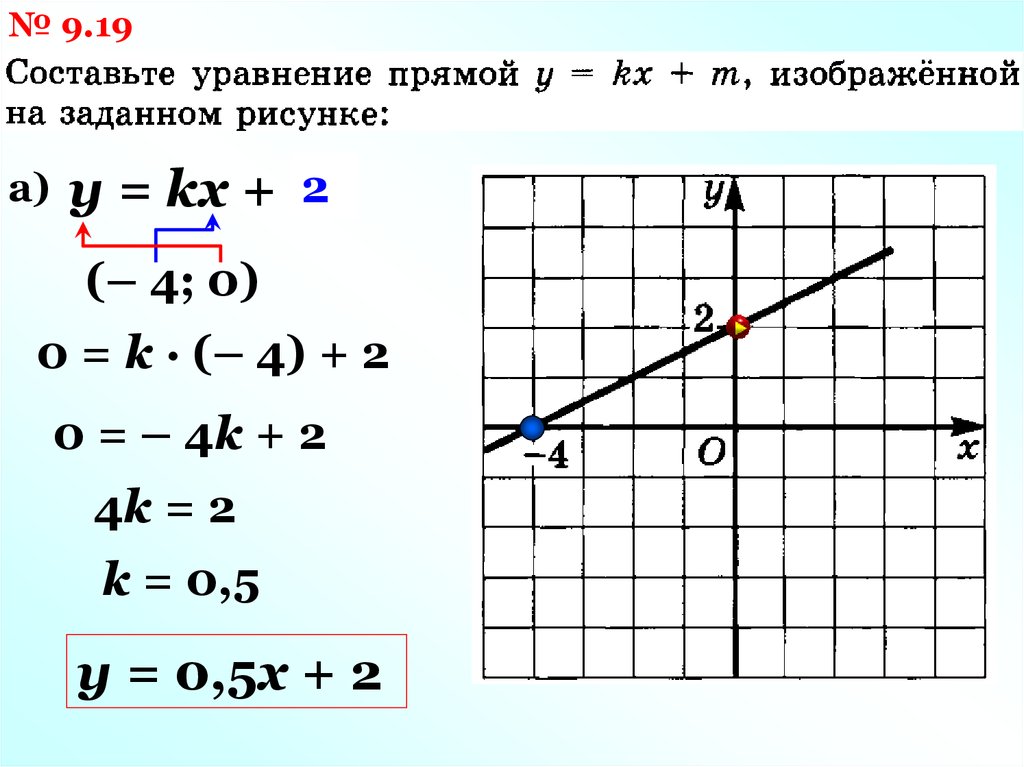
№ 9.19
а)
2
y = kx + m
(– 4; 0)
0 = k · (– 4) + 2
0 = – 4k + 2
4k = 2
k = 0,5
y = 0,5x + 2

23.

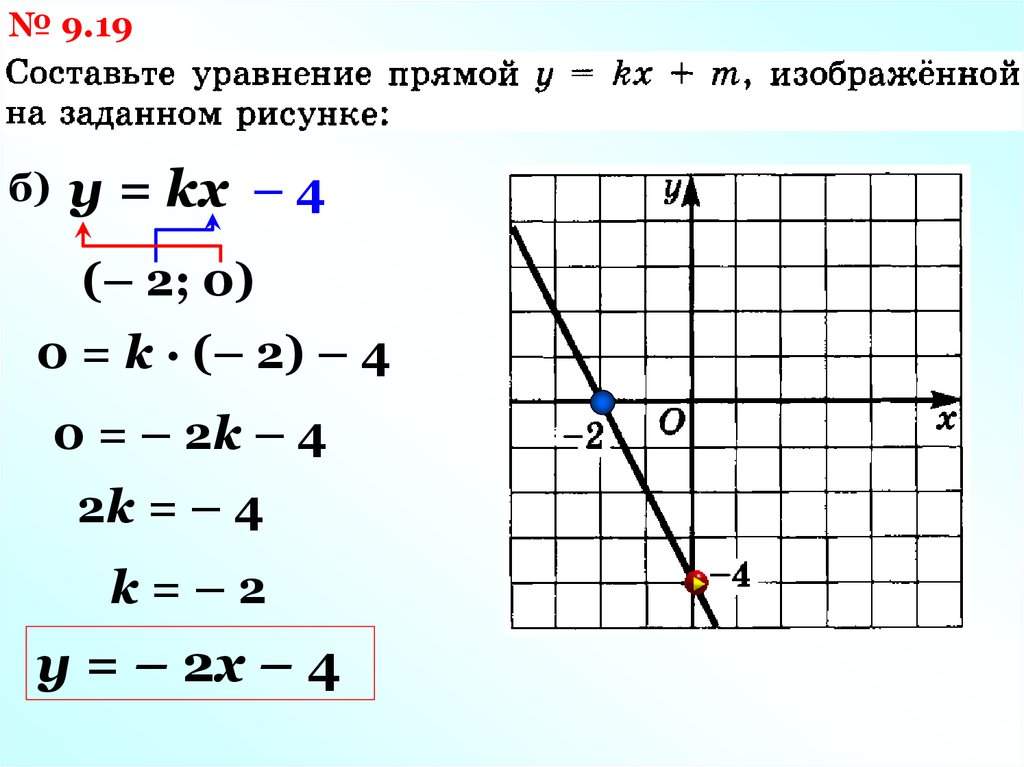
№ 9.19
б)
–m
4
y = kx +
(– 2; 0)
0 = k · (– 2) – 4
0 = – 2k – 4
2k = – 4
k=–2
y = – 2x – 4

24.

№ 9.19
в)
–m
4
y = kx +
(6; 0)
0=k·6–4
0 = 6k – 4
– 6k = – 4
2
у х 4
3
2
k
3

25.

№ 9.19
г)
2
y = kx + m
(2; – 1)
–1=k·2+2
– 1 = 2k + 2
– 2k = 3
k = – 1,5
y = – 1,5x + 2

26.

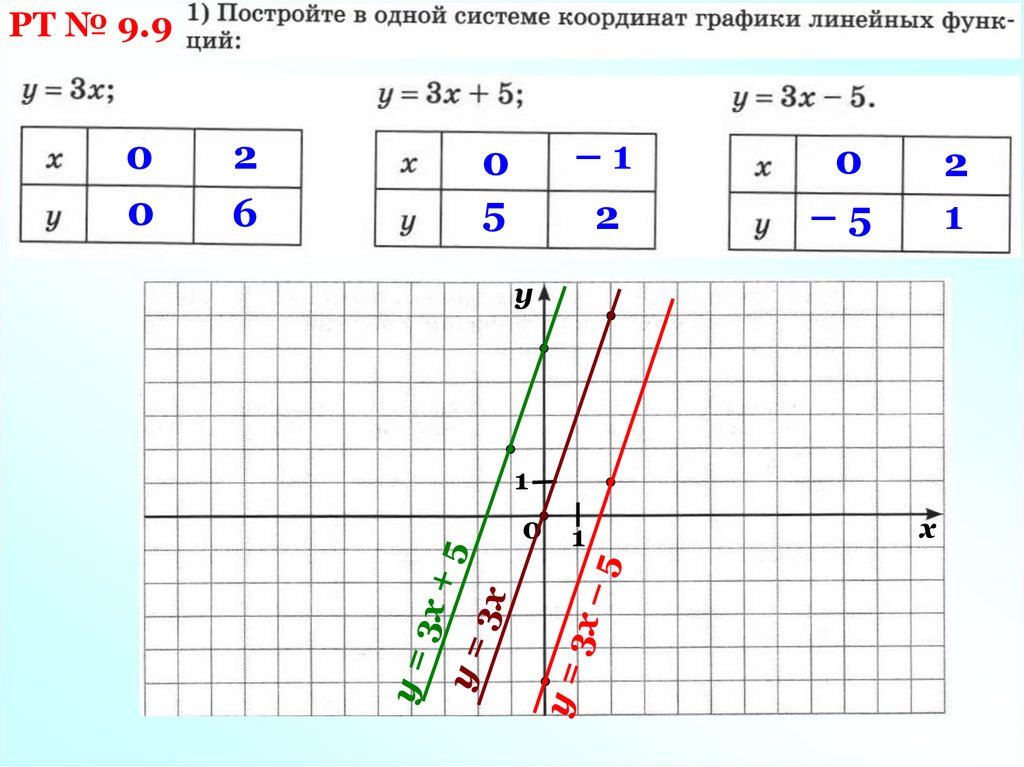
РТ № 9.9
0
0
2
6
–1
0
5
2
0
–5
2
1
у
1
0 1
х

27.

РТ № 9.9
у
1
0 1
параллельно
х

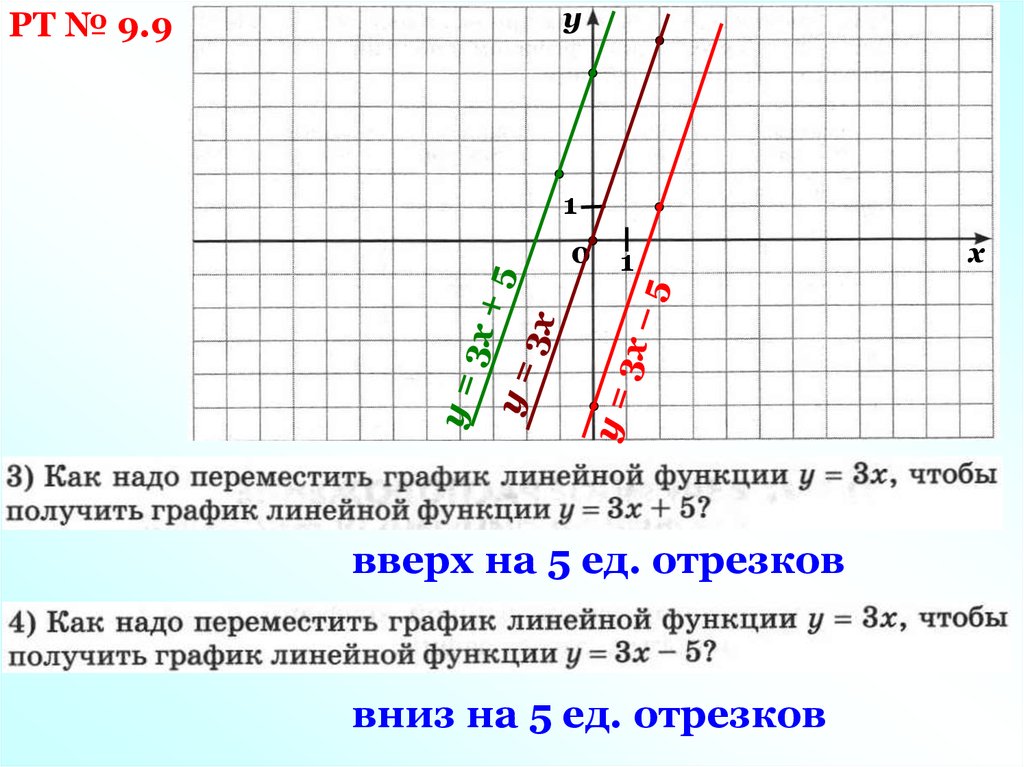
28.

РТ № 9.9
у
1
0 1
вверх на 5 ед. отрезков
вниз на 5 ед. отрезков
х

29.

№ 9.17(а,б) Выясните, корректно ли задание: найти
точку пересечения указанных прямых.
Если задание корректно, то выполните
его.
прямые параллельны

30.

№ 9.17(а,б) Выясните, корректно ли задание: найти
точку пересечения указанных прямых.
Если задание корректно, то выполните
его.
прямые пересекаются
у
1
0
Ответ: (– 1; – 3)
1
х

31.

№ 9.19
а)
2
y = kx + m
(– 4; 0)
0 = k · (– 4) + 2
0 = – 4k + 2
4k = 2
k = 0,5
y = 0,5x + 2

32.

№ 9.19
б)
–m
4
y = kx +
(– 2; 0)
0 = k · (– 2) – 4
0 = – 2k – 4
2k = – 4
k=–2
y = – 2x – 4

33.

№ 9.19
в)
–m
4
y = kx +
(6; 0)
0=k·6–4
0 = 6k – 4
– 6k = – 4
2
у х 4
3
2
k
3

34.

№ 9.19
г)
2
y = kx + m
(2; – 1)
–1=k·2+2
– 1 = 2k + 2
– 2k = 3
k = – 1,5
y = – 1,5x + 2