Similar presentations:
Преобразование числовых выражений, содержащих корень n-ой степени
1. 12.09.11. Классная работа
Преобразование числовых выражений,содержащих корень n – ой степени
a b, b a
2
n
,
n
а
где n- показатель корня,
а- подкоренное выражение.
Знак
называют еще радикалом
a b, b a
n
2. Вычислить:
38
4
16
5
1
;
32
4
81
;
625
3. Уравнение
х аn
Уравнение
при нечетном n имеет единственное
n
решение
х=
а
Например : х3=-125;
х=
3
.
125
х=- 3 125
х=-5.
;
4. Уравнение
х апри четном n имеет и
положительном а имеет два
корня
Например:
n
n
х=±
х4=16;
a
х1=
.
4
16
;
х2=-
4
.
;
х1=2;
х2=-2.
16
5. Решить уравнение:
а) х 56
б)х 5
3
в )0,1х 10 0
3
6. Свойства корня n – ой степени
7. Свойства корня n – ой степени
nx х, если n нечетно.
n
x
n
n
|х|, если n четно.
8.
Например :.
Так как
3 2
2
3 2
3 1,7, то 3 2 <0, следовательно
3 2 3 2 3 2 2 3
.
9.
10.
11.
12.
13.
14. Материалы ЕГЭ
510 2 17 5 10 2 17 Вычислить
2 x 4 3 x Внести множитель под корень
6
3
4
128 a Вынести множитель из под корня
7
1
Избавиться от иррациональности в знаменателе
3
3 2
2 5
4
5
2 5
5
упростить
15. Дома
Ч.2с.7 № 10,с.8 №14,15




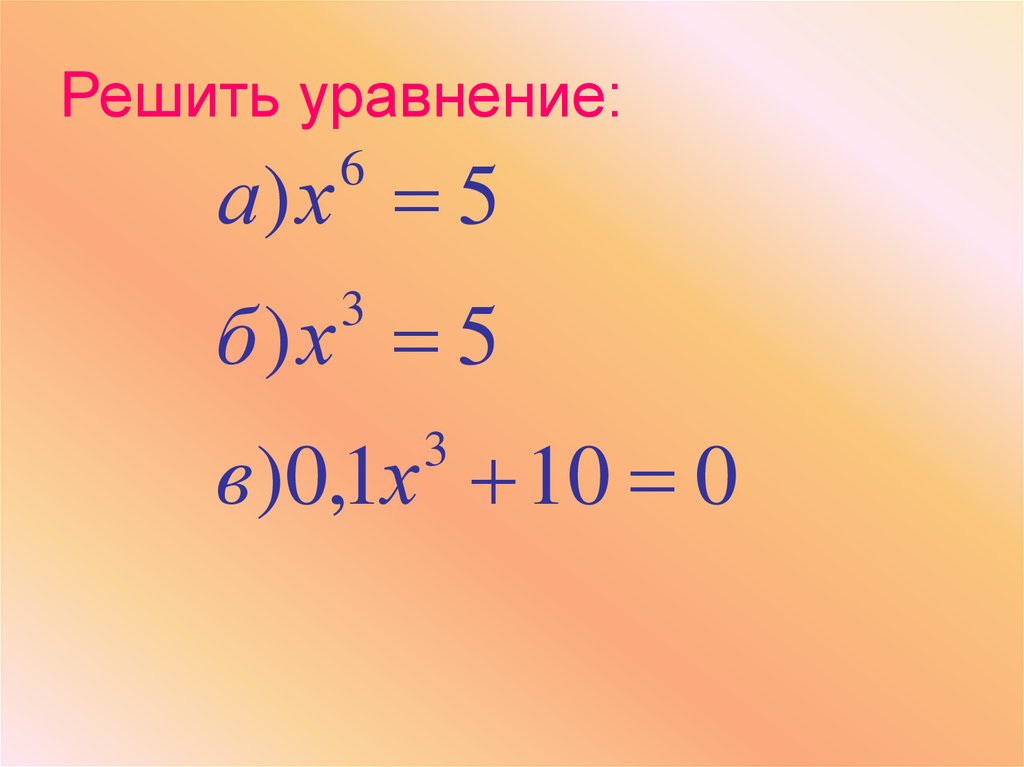










 mathematics
mathematics