Similar presentations:
Функция у х, её свойства и график
1.
Функцияу х,
её свойства и график.
2.
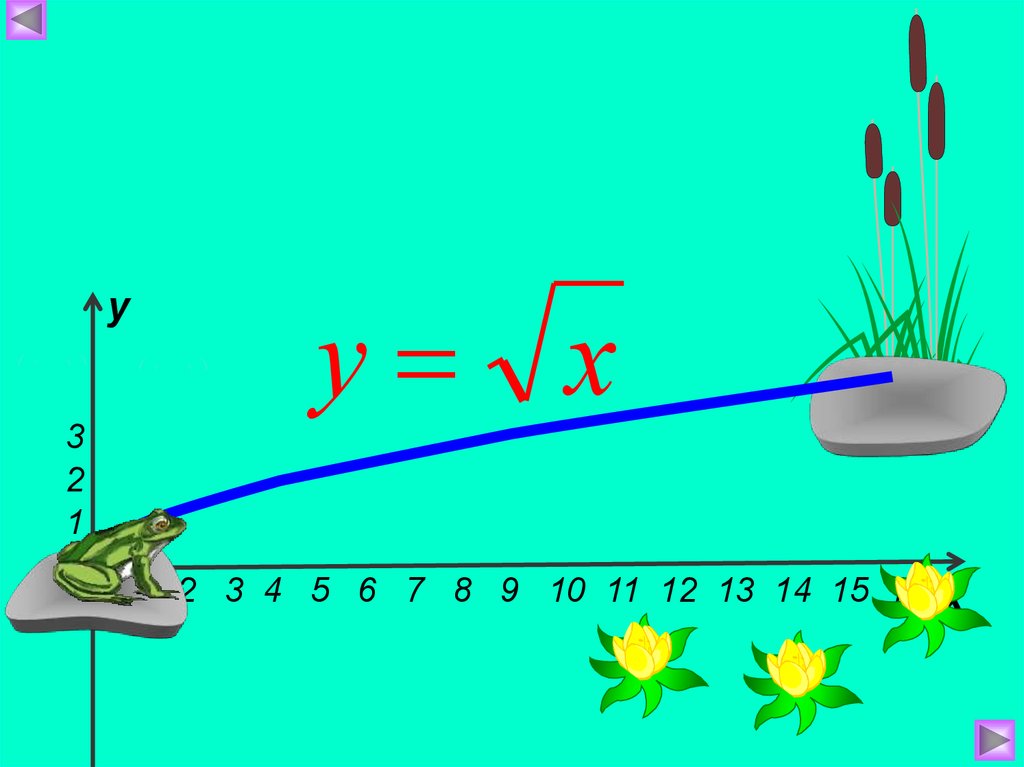
уу х
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 х
3.
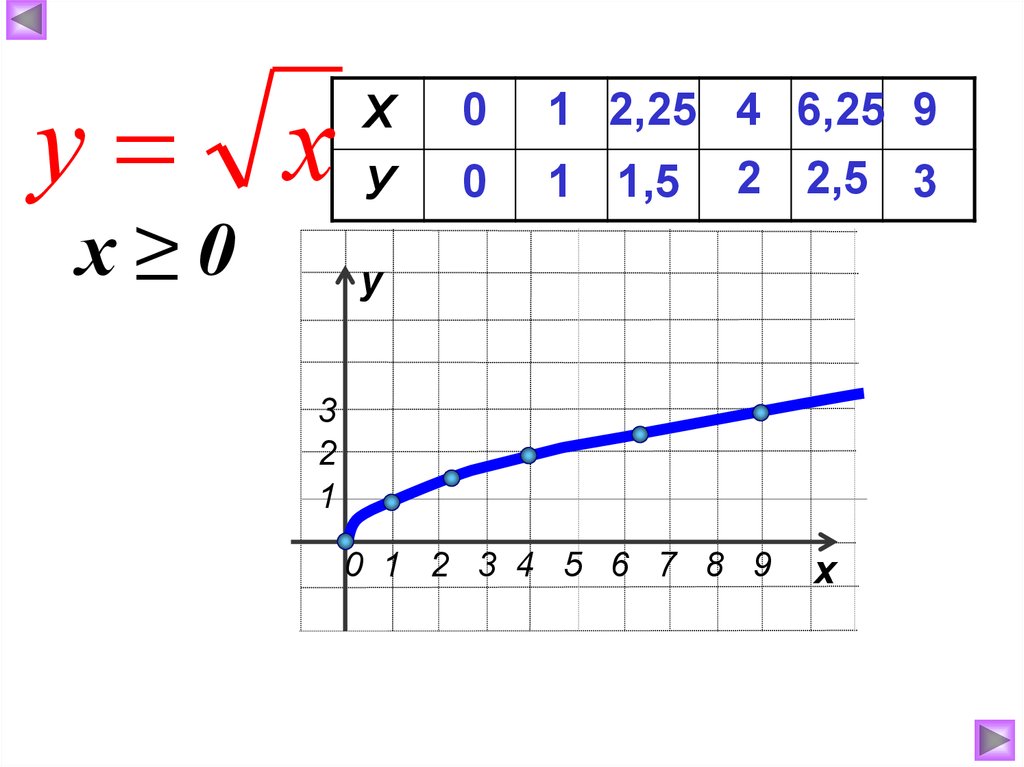
у хх≥0
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х
4.
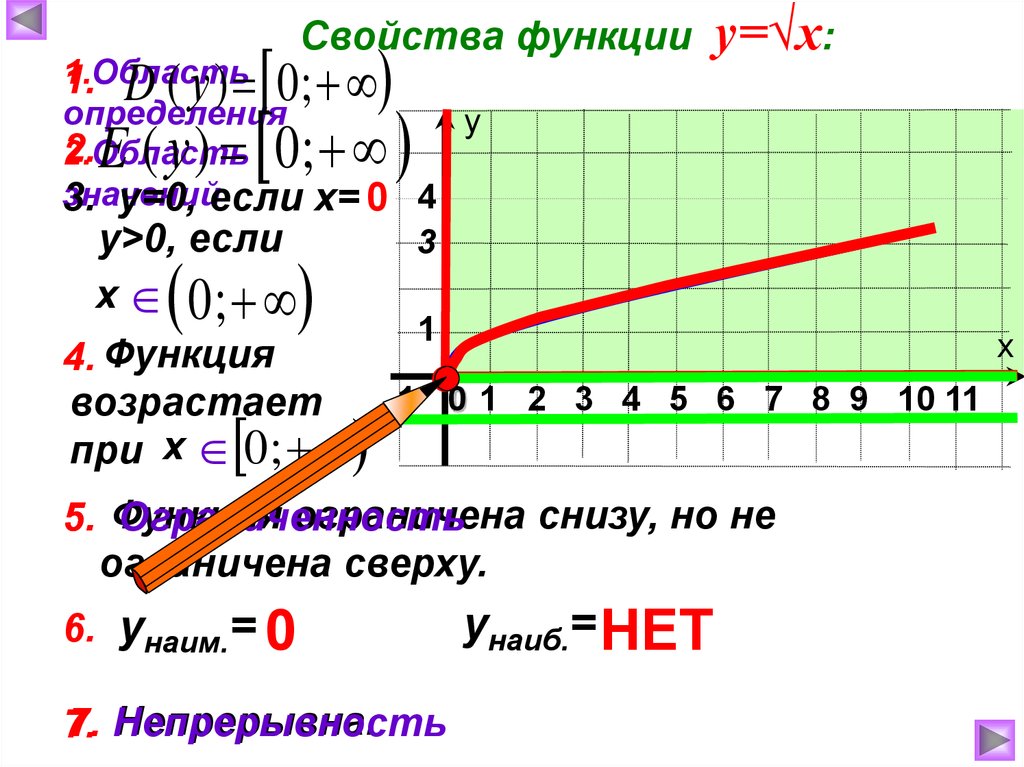
Свойства функции1.Область
1. D ( у ) 0 ;
определения
у
2.
2.Область
значений
3. у=0, если х= 0 4
у>0, если
3
у=√х:
E ( у ) 0;
х 0;
1
х
4. Функция
-1 0 1 2 3 4 5 6 7 8 9 10 11
возрастает
при х 0 ;
ограничена снизу, но не
5. Функция
Ограниченность
ограничена сверху.
6. унаим.= 0
Непрерывна.
7. Непрерывность
7.
унаиб.= НЕТ
5.
у хх≥0
Х
0
У
0
1 2,25 4 6,25 9
-1 -1,5 -2 -2,5 -3
у
х
-1
-2
-3
-4
0 1 2 3 4 5 6 7 8 9 10 11
6.
Свойства функции1.Область
1. D ( у ) 0 ;
определения
2.
2.Область
значений
3. у=0, если х= 0
E ( у ) ; 0
у<0, если
х 0;
4. Функция
убывает
при х 0 ;
-1
-2
-3
-4
у=-√х:
у
х
0 1 2 3 4 5 6 7 8 9 10 11
ограничена сверху, и не
5. Функция
Ограниченность
ограничена снизу.
6. унаим.= НЕТ
Непрерывна.
7. Непрерывность
7.
унаиб.= 0
7.
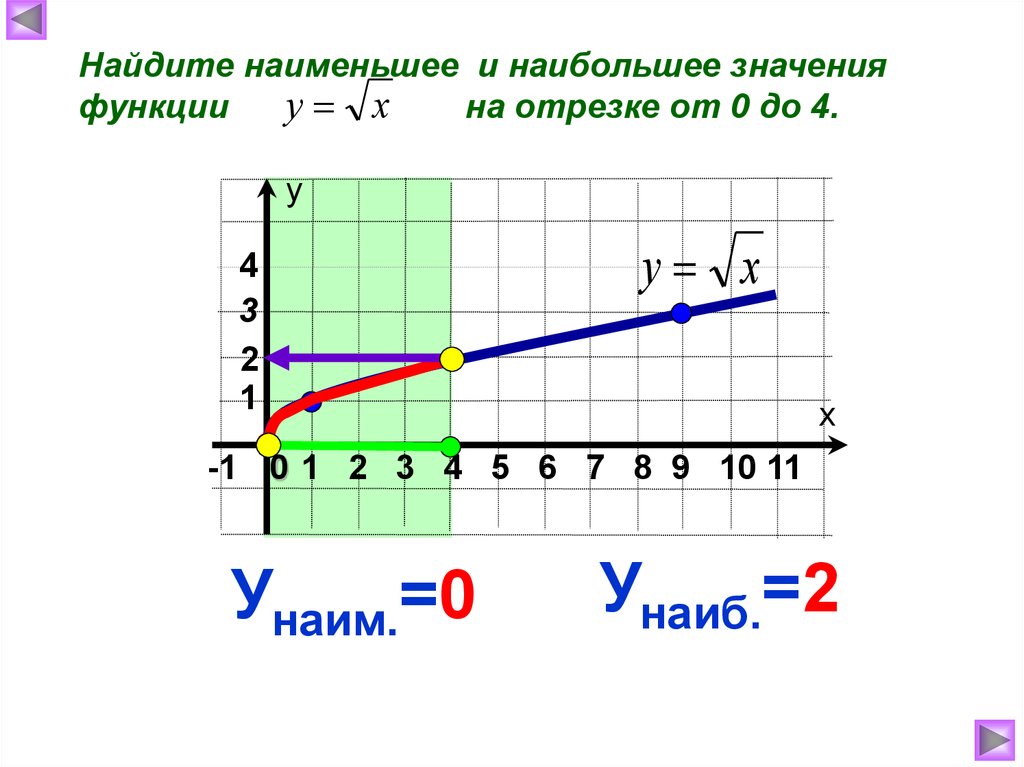
Найдите наименьшее и наибольшее значенияу х
функции
на отрезке от 0 до 4.
у
4
3
2
1
у х
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=0
Унаиб.=2
8.
Решить графически уравнение:√х=х-6
1
4
3
2
Построим в одной системе
координат графики функций:
у=√х
у=х-6
Х 0 6
У -6 0
2
3
у х
1
-1
-2
-3
-4
-5
-6
Х 0 1 4 9
У 0 1 2 3
у
х
0 1 2 3 4 5 6 7 8 9
у=х-6
Найдём абсциссы точек
пересечения графиков
ОТВЕТ:
х=9
9.
Построить и прочитать график функции y=f(x),x , если 0 x 4;
где f ( x)
Решение:
6 x, если 4 x 8.
1. Область определения функции — отрезок [0; 8].
2. у = 0 при х = 0 и при х = 6; у > 0 при 0 < х < 6;
у < 0 при 6 x 8.
3. Функция возрастает на отрезке [0; 4] и убывает на отрезке [4; 8].
4. унаим = -2 (достигается в точке х = 8),
унаиб = 2 (достигается в точке х = 4).
5. Функция непрерывна в заданной области определения.
6. Область значений функции — отрезок [-2; 2].
Игорь Жаборовский © 2012
UR OK IMATE MATIK I.R U
10.
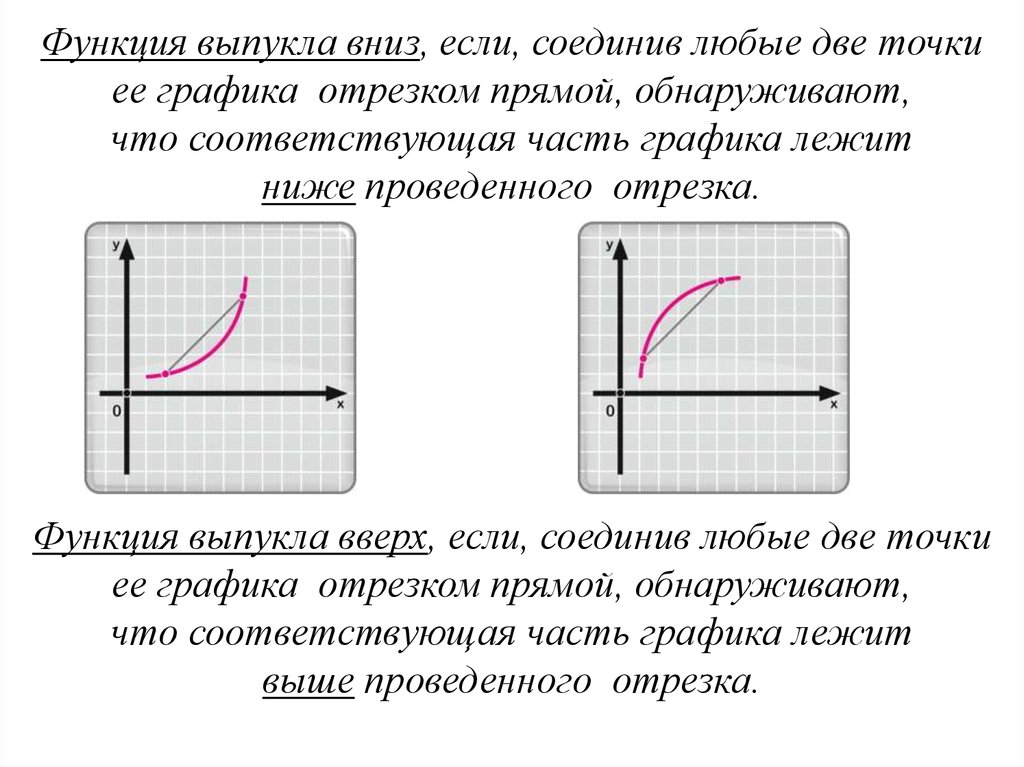
Функция выпукла вниз, если, соединив любые две точкиее графика отрезком прямой, обнаруживают,
что соответствующая часть графика лежит
ниже проведенного отрезка.
Функция выпукла вверх, если, соединив любые две точки
ее графика отрезком прямой, обнаруживают,
что соответствующая часть графика лежит
выше проведенного отрезка.





 mathematics
mathematics