Similar presentations:
решение неравенств второй степени с помощью графика квадратичной функции
1. Может ли помочь график квадратичной функции при решении этого неравенства?
x 2 x 48 02
2. 01.12.2014 г.
3.
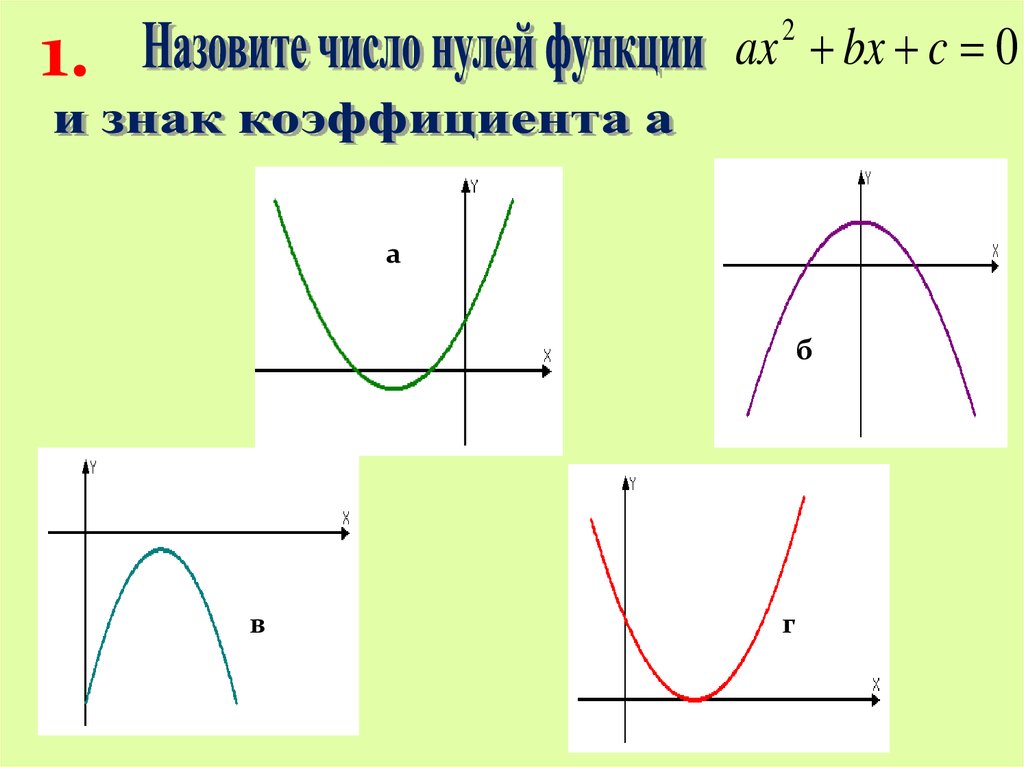
ax bx c 01.
2
а
б
в
г
4.
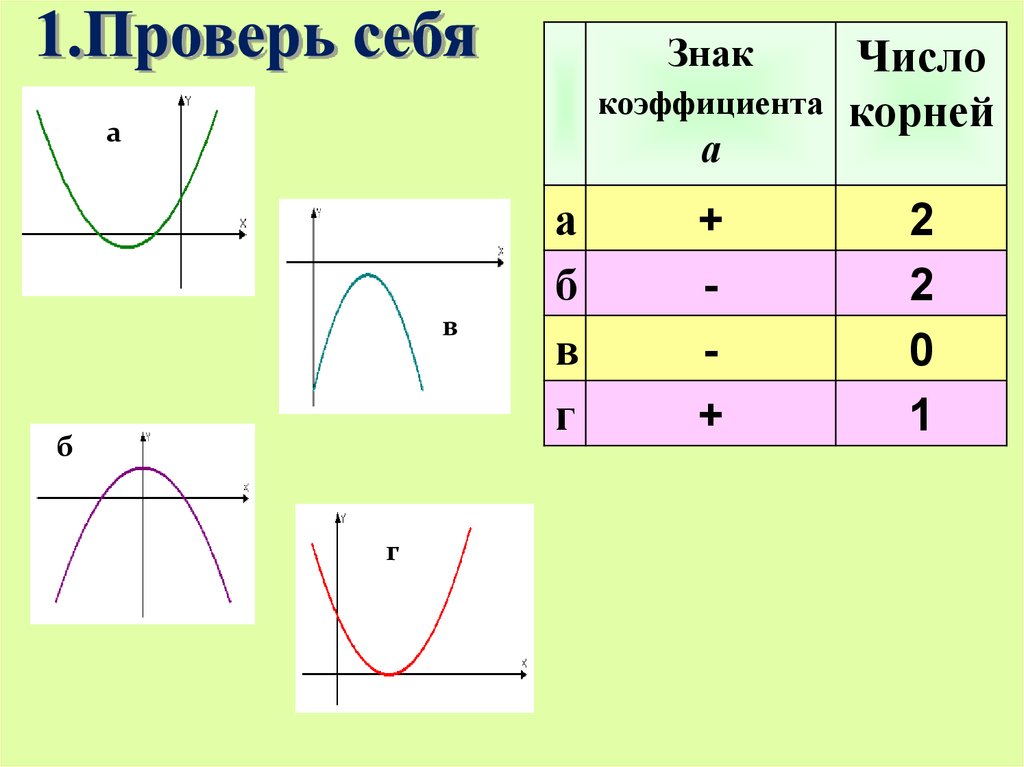
Знаккоэффициента
а
а
в
б
г
а
б
в
г
+
+
Число
корней
2
2
0
1
5. 2. Найдите корни квадратного трехчлена
а) x x 122
б) x 6x 9
2
6.
2.Найдите корни квадратноготрехчлена:
2
х +х-12;
а)
x1=-4; x2=3
2
б) х +6х+9; x1,2=-3
7.
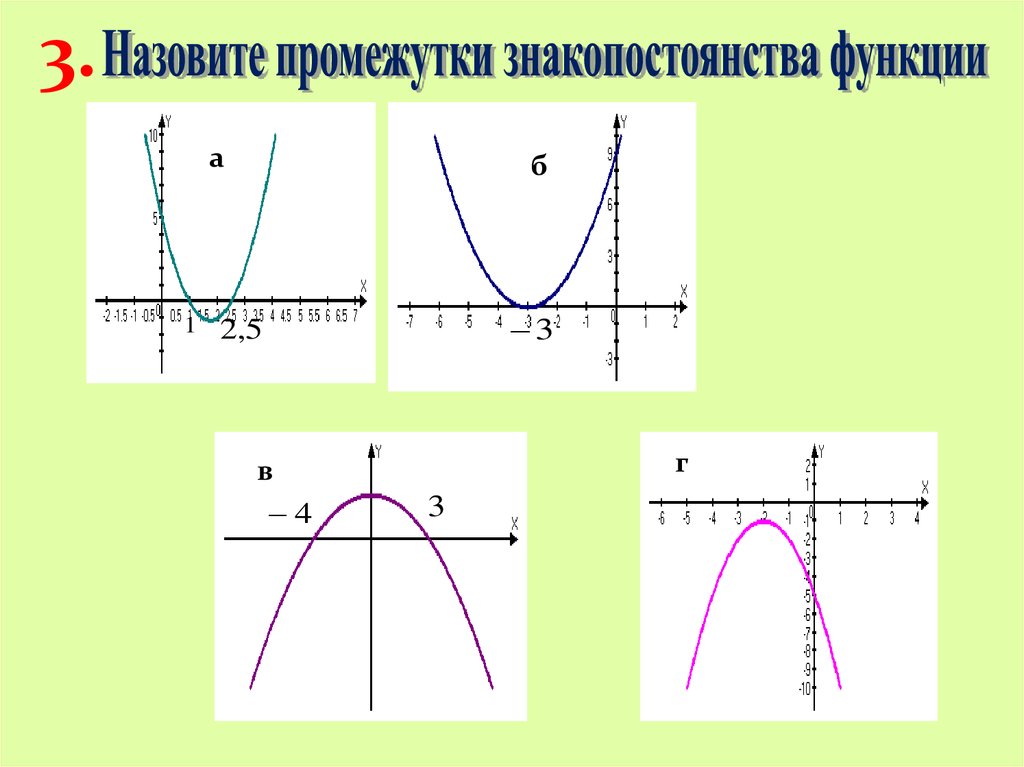
3.а
1
б
3
2,5
г
в
4
3
8.
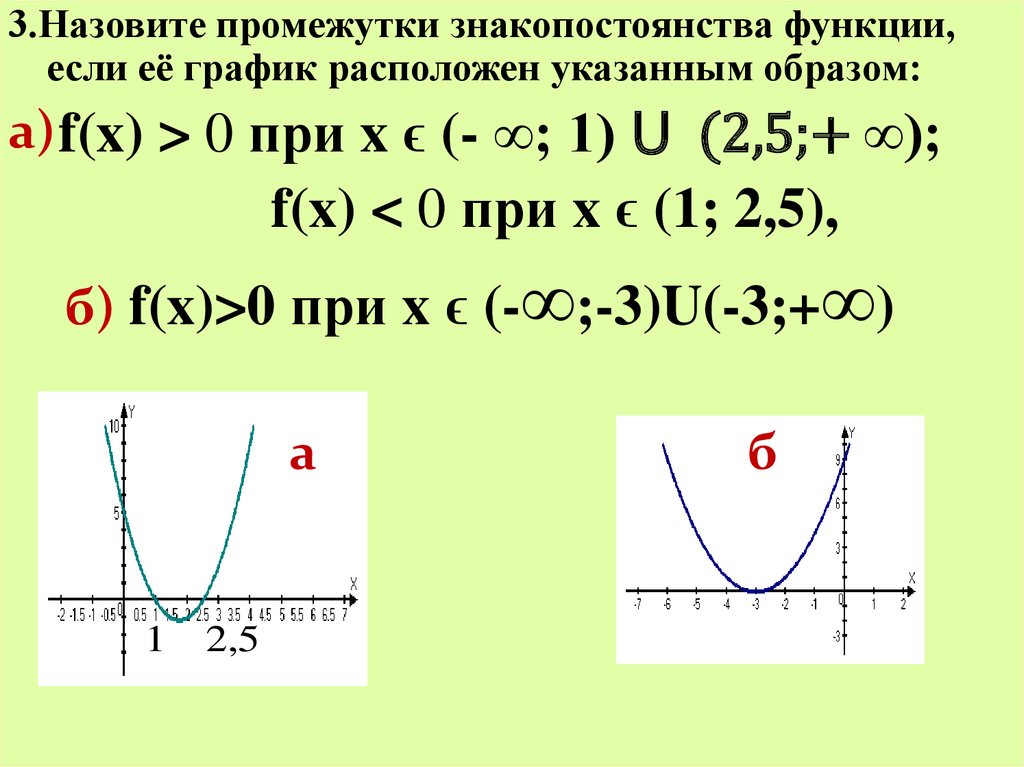
3.Назовите промежутки знакопостоянства функции,если её график расположен указанным образом:
а) f(x) > 0 при x ϵ (- ∞; 1) ⋃ (2,5;+ ∞);
f(x) < 0 при x ϵ (1; 2,5),
б) f(x)>0 при x ϵ (-∞;-3)U(-3;+∞)
а
1
2,5
б
9.
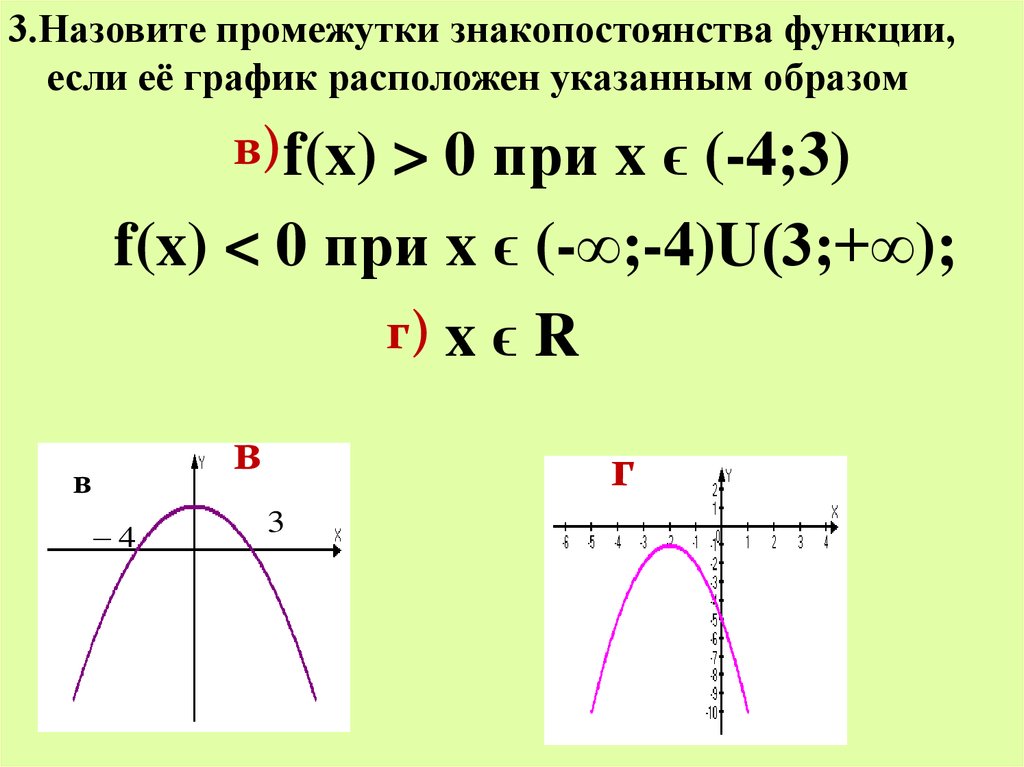
3.Назовите промежутки знакопостоянства функции,если её график расположен указанным образом
0 при x ϵ (-4;3)
f(x) < 0 при x ϵ (-∞;-4)U(3;+∞);
г) x ϵ R
в)f(x) >
в
в
б
г
3
4
2
10. 1.Привести неравенство к виду ax^2 + bx + c >0 (f(x)<0; f(x)≤0; f(x)≥0) 2.Рассмотреть функцию y = ax^2 + bx + c 3.Определить
11.
Высота подъема тела над землей h, начальнойвысотой тела над землей h0, начальной
скоростью v0, ускорением свободного падения
g, углом наклона струи воды α:
Так как h > 3
12.
>3L – дальность полета, α = 45°, L>3.
13.
14.
Решитьнеравенство:
2
1. 5х +9х-2<0
15.
5х2+9х-2<02. Рассмотрим функцию
2
y=5х +9х-2
16.
5х2+9х-2<02.Рассмотрим функцию
y=5х2+9х-2
3. Графиком функции
является парабола, ветви
которой направлены вверх.
17.
25х +9х-2<0
2.Рассмотрим функцию
y=5х2+9х-2
3. Графиком функции является
парабола, ветви которой
направлены вверх.
4. Нули функции: 5х2+9х-2=0
х1=-2; х2=5.
18.
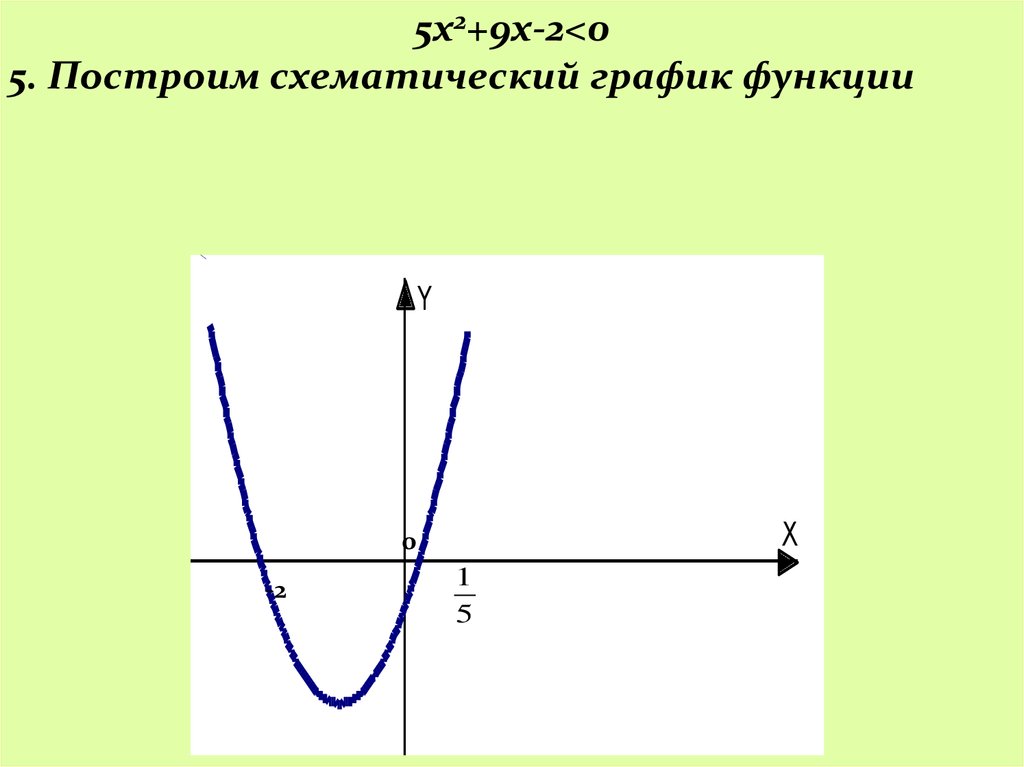
5х2+9х-2<05. Построим схематический график функции
Y
X
0
-2
1
5
19.
5х2+9х-2<06. Выделим часть параболы,
для которой y < 0
Y
1
5
-2
XX
0
1
5
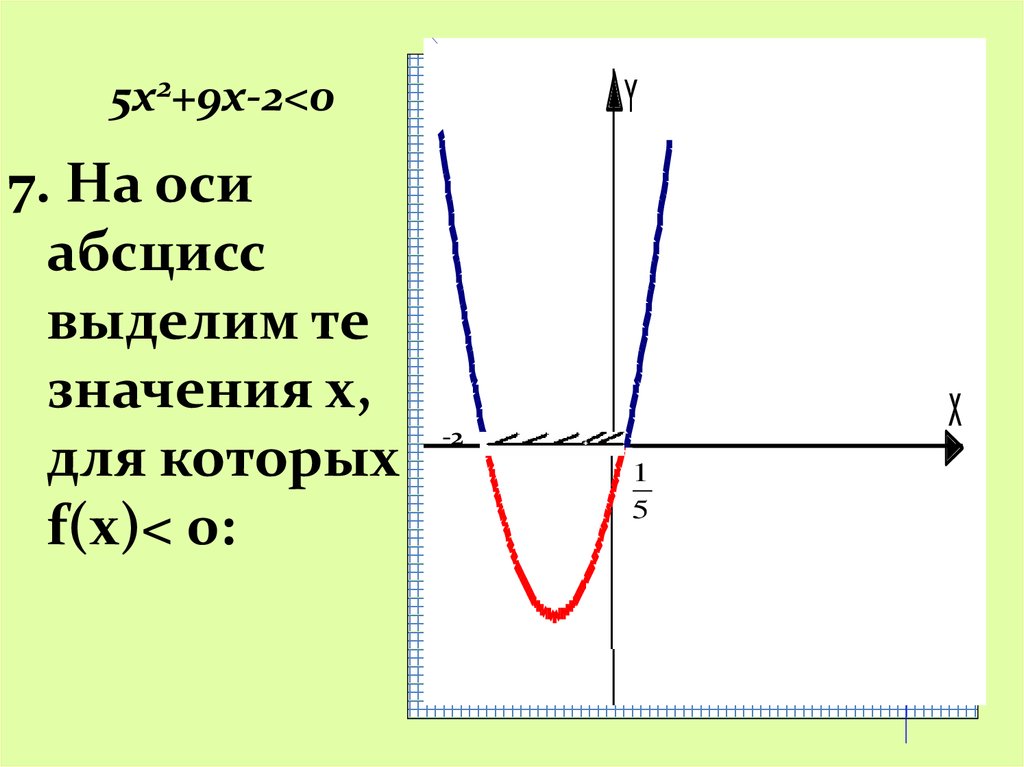
20.
5х2+9х-2<07. На оси
абсцисс
выделим те
значения x,
для которых
f(x)< 0:
YY
XX
-2
1
5
-2
0
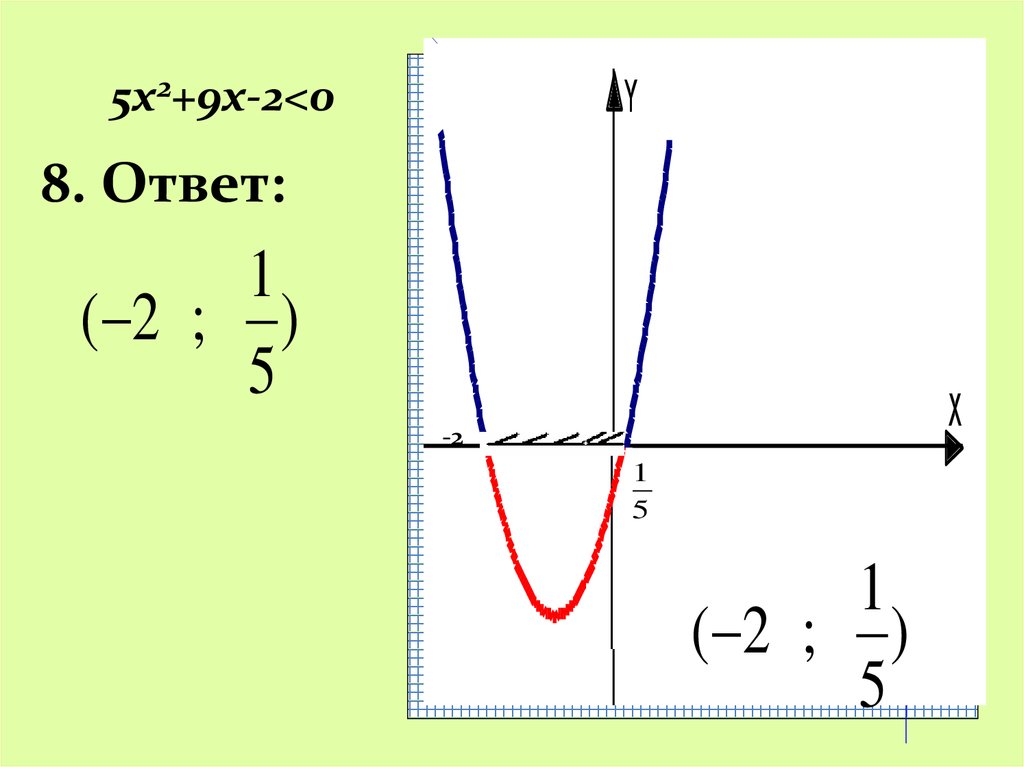
21.
5х2+9х-2<0YY
8. Ответ:
1
( 2 ; )
5
XX
-2
1
5
-2
0
1
( 2 ; )
5
22.
Решите неравенство:2.
x 5 x 6 0.
2
//////
////// //////
3 x 6
1
x
//////
2 3
x
//////
2
////// /////
3 x
2
///// //////
3 x 3
//////
4 x
23.
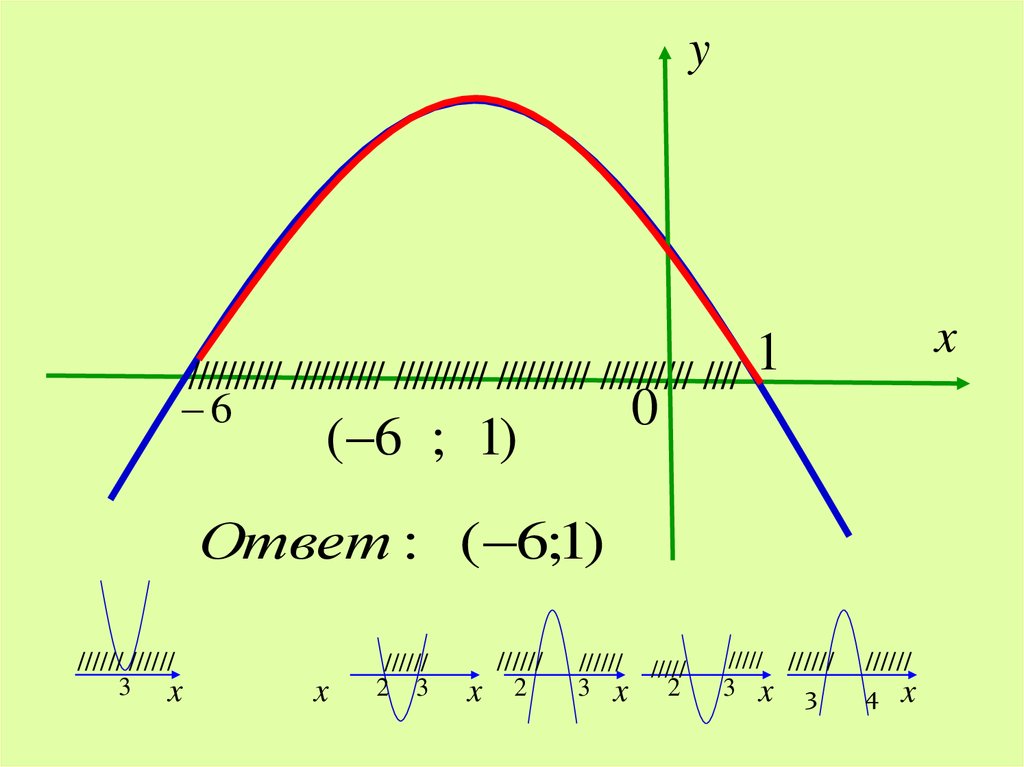
yx
1
////////// ////////// ////////// ////////// ////////// ////
6
0
( 6 ; 1)
Ответ : ( 6;1)
////// //////
3 x
x
//////
2 3
x
//////
2
////// /////
3 x
2
///// //////
3 x 3
//////
4 x
24.
Решите неравенства:3.
4.
x 5 x 6 0.
2
x 7 x 12 0.
2
Для успевающих:
.2
x 6 x 9 0.
№316
//////
////// //////
3 x 6
1
x
//////
2 3
x
//////
2
////// /////
3 x
2
///// //////
3 x 3
//////
4 x
25.
Проверьте себя:2
х−
3)
5х + 6 > 0
Ответ: (−∞; 2); (3;+∞)
2
4)−х + 7х−12<0
Ответ: (−∞; 3); (4;+∞)
2
х − 6х + 9 >0
Ответ: (−∞; 3);(3;+∞)
26. Какой промежуток будет являться решением неравенства?
( x 3) 02
27.
Крайниепромеж:
Средний
(−∞;); промеж:
(; )
(;+∞)
1. x 2 x 48 0
2
2. x 2 2 x 48 0
3. x 2 10 x 25 0
4. x 10 x 25 0
2
5. x 2 2 x 15 0
6. x 2 x 15 0
2
x = x0
x≠x0
x∈R
∅
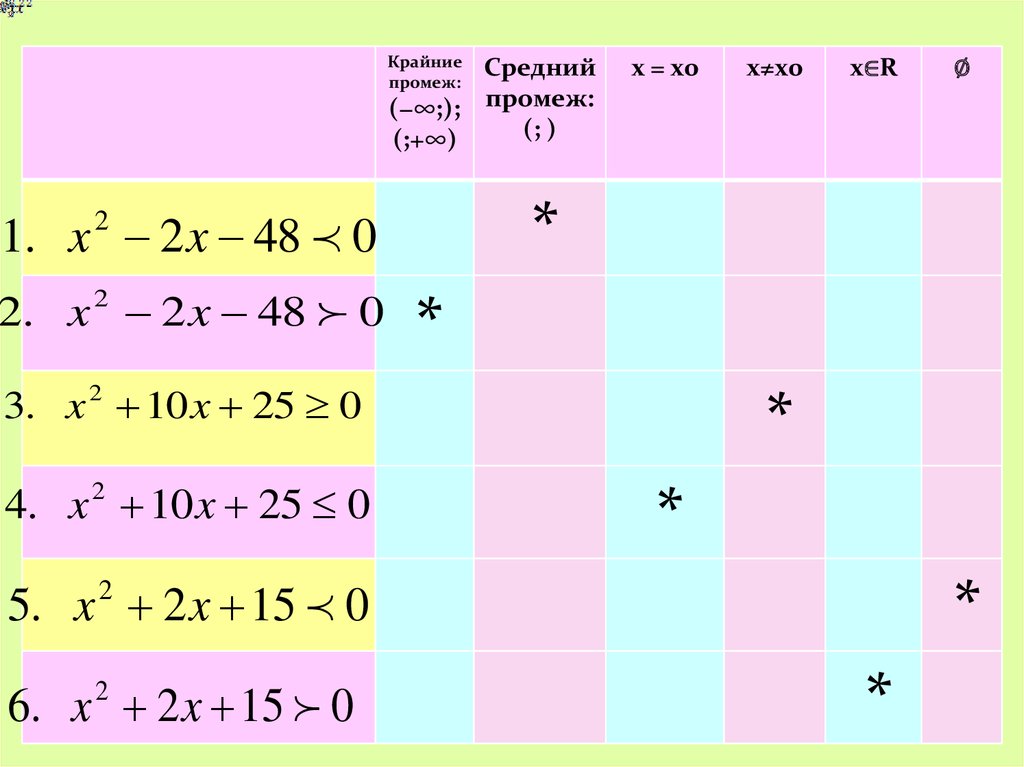
28.
Крайниепромеж:
Средний
(−∞;); промеж:
(; )
(;+∞)
4. x 10 x 25 0
x∈R
*
*
5. x 2 2 x 15 0
6. x 2 x 15 0
2
∅
*
3. x 2 10 x 25 0
2
x≠x0
*
1. x 2 x 48 0
2
2. x 2 2 x 48 0
x = x0
*
*
29.
30. Проверьте себя:
31. Задание на самоподготовку:
32.
Спасибоза
внимание!
















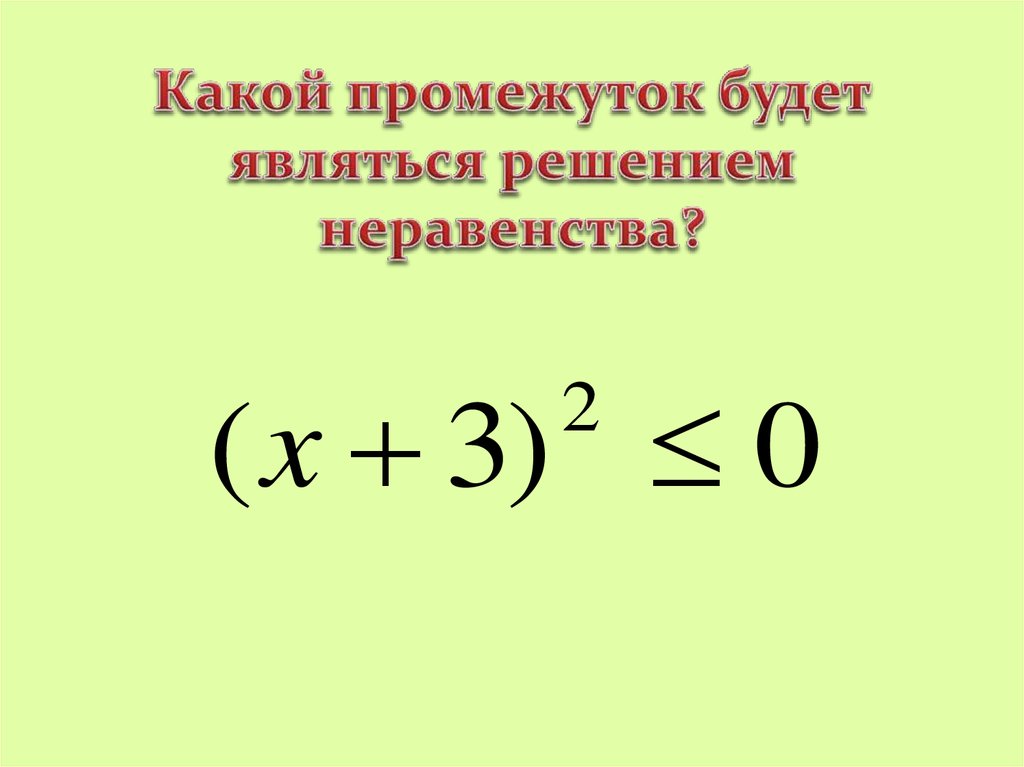






 mathematics
mathematics








