График квадратичной функции. Неравенства с одной переменной

1.

Темы: График
квадратичной функции.
Неравенства с одной
переменной.
Презентацию подготовила
ученица 9 класса
МОУ «СОШ №6»
Шумская Нина.
Руководитель Богдановская В.М.

2. Квадратичная функция и ее график.

Квадратичной функцией называется функция, которую можно
задать формулой вида y = ax² + bx + c, где х – независимая
переменная, a,b,c -некоторые числа, причём a ≠ 0.
Графиком квадратичной функции является парабола
Алгоритм построения параболы.
1)
2)
3)
4)
5)
f(x) = ax² + bx + c
Направление ветвей
Вершина ( x = -b ∕ 2a; y = f(x ). )
Ось симметрии.
Таблица значений
Построение графика

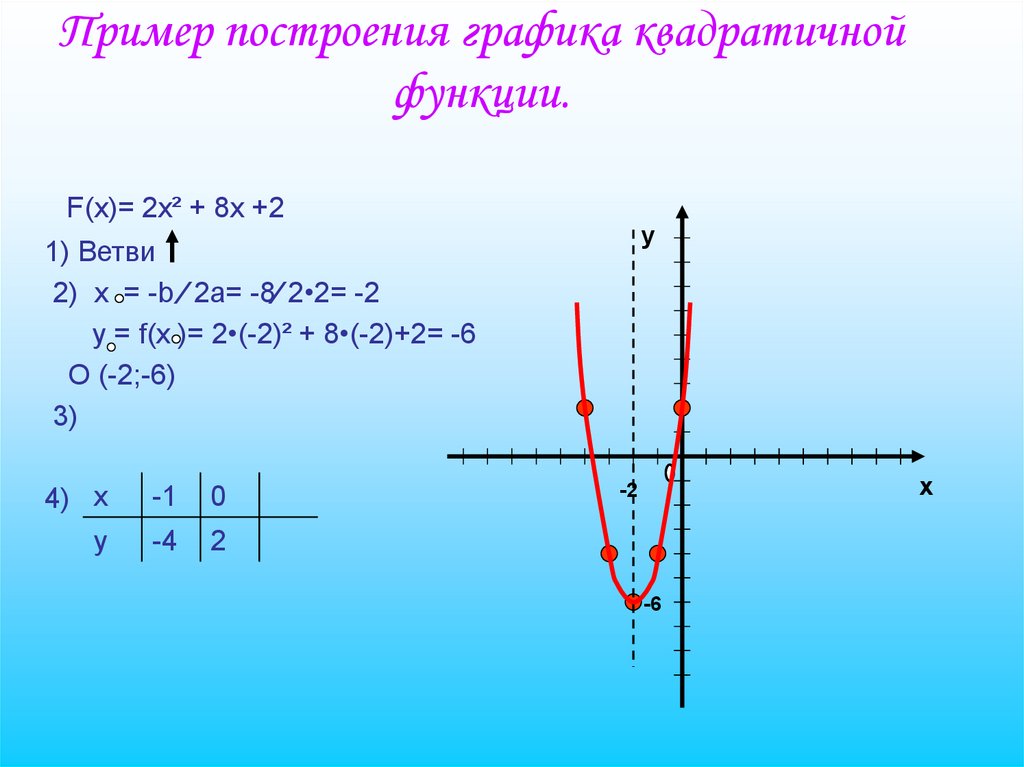
3. Пример построения графика квадратичной функции.

F(x)= 2x² + 8x +2
у
1) Ветви
2) х = -b ∕ 2a= -8∕ 2•2= -2
y = f(x )= 2•(-2)² + 8•(-2)+2= -6
O (-2;-6)
3)
4) х
у
-1
0
-4
2
х
-2
-6

4. Неравенства второй степени с одной переменной.

Неравенства вида ax²+bx+c>0 и ax²+bx+c<0,
где х – переменная, a,b,c – некоторые числа, причём а ≠ 0,
называют неравенствами второй степени с одной
переменной.
Алгоритм решения квадратного неравенства.
1) Вводим функцию (у…..),
2) Находим нули функции (у=0),
3) Определяем направление ветвей,
4) Делаем схематический рисунок ,
5) Выбираем ответ.

5. Пример решения квадратного неравенства.

5х²+9х-2<0
1) у = 5х²+9х-2
2) 5х²+9х-2=0
D=81-4•5•(-2)=121
Х= 1/5;
Х = -2
3) Ветви ↑
5)
Х є(-2;1/5)
Ответ: (-2;1/5)
4)
-2
1/5
х

6. Спасибо за внимание!