Неравенства с двумя переменными и их системы

1.

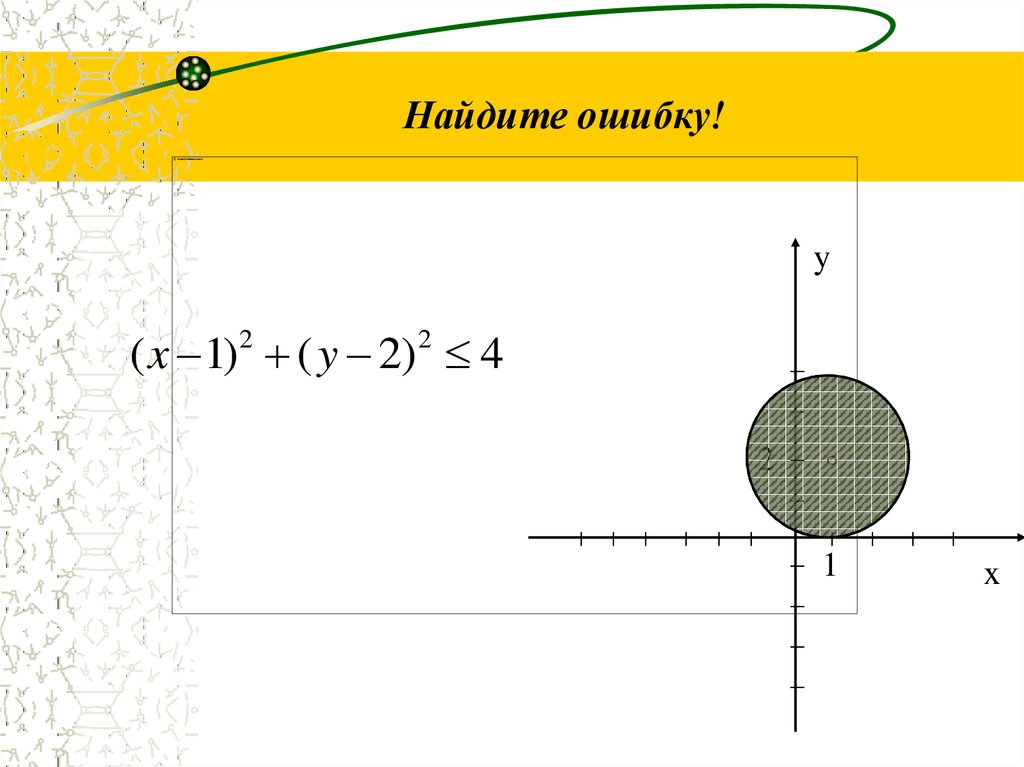
Урок 3

2. Найдите ошибку!

y
6
у х 4
2
4
2
-6
-4
-2
0
2
-2
-4
x

3. Найдите ошибку!

y
|
2
|
|
|
( x 1)2 ( y 2)2 4
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
x

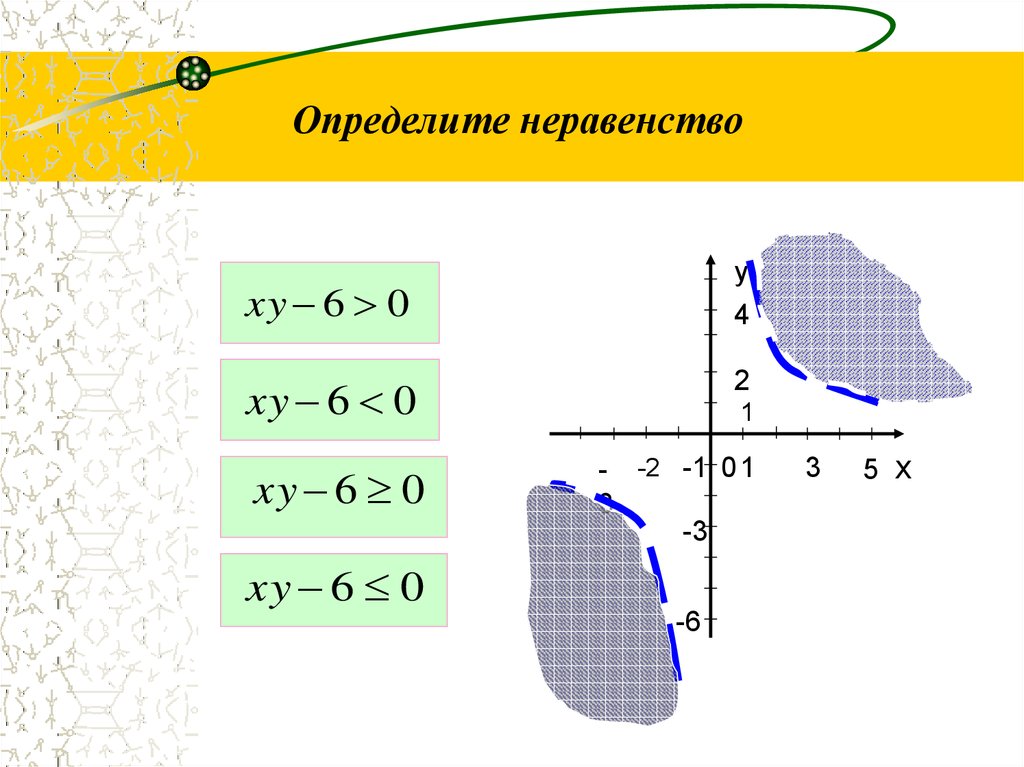
4. Определите неравенство

у
xy 6
8
00
4
xy 6 0
2
xy 6 0
- -2 -1 0 1
3
-3
1
xy 6 0
-6
3
5 х

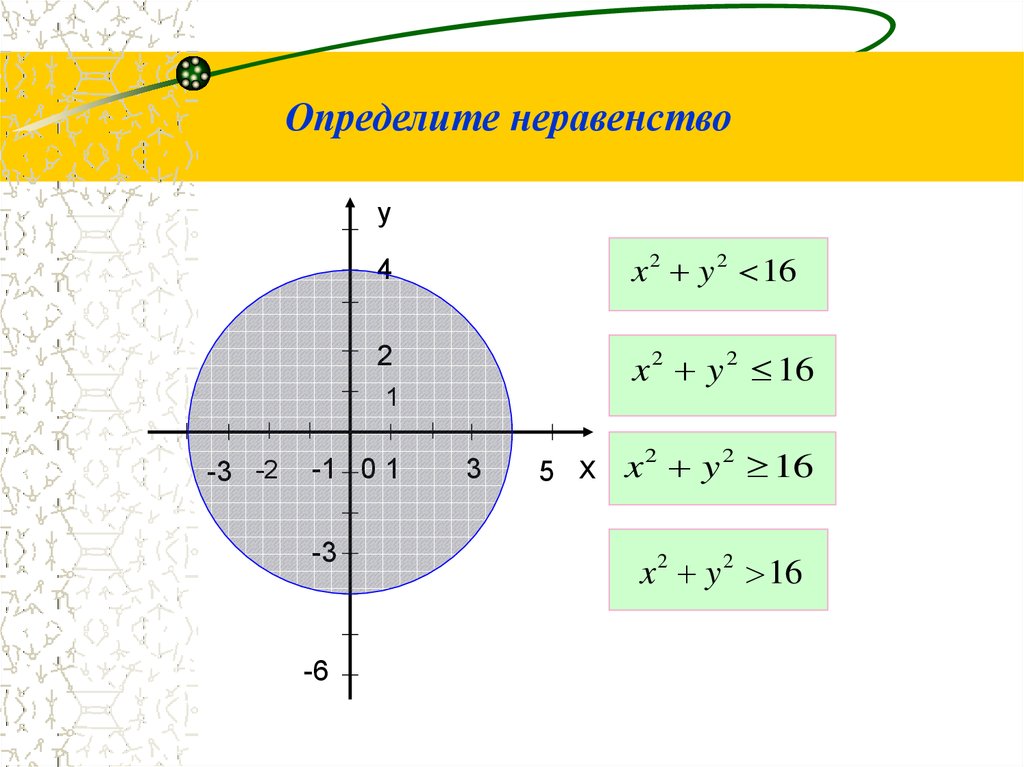
5.

Определите неравенство
у
4
x 2 y 2 16
2
x 2 y 2 16
1
-3 -2
-1 0 1
-3
-6
3
5 х
x 2 y 2 16
x 2 y 2 16

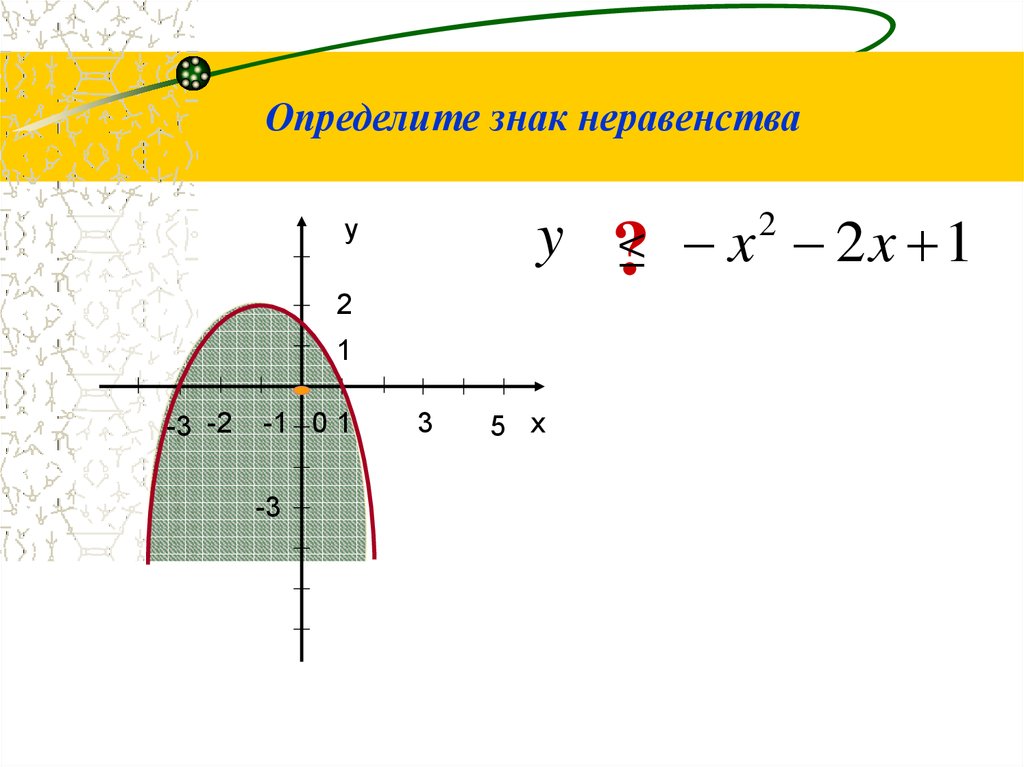
6.

Определите знак неравенства
y
у
2
1
-3 -2
-1 0 1
-3
3
5 х
?≤
x 2x 1
2

7. Решить графически систему неравенств

y
x y 4 0,
y 0,
x 0
2
2
2
1
-2
-1
1
0
-1
-2
2
x

8. Неравенства и системы неравенств высших степеней с двумя переменными

№1. Изобразите на координатной плоскости множество точек,
задаваемых системой неравенств
x y 25,
2
2 y x 1 0.
2
2

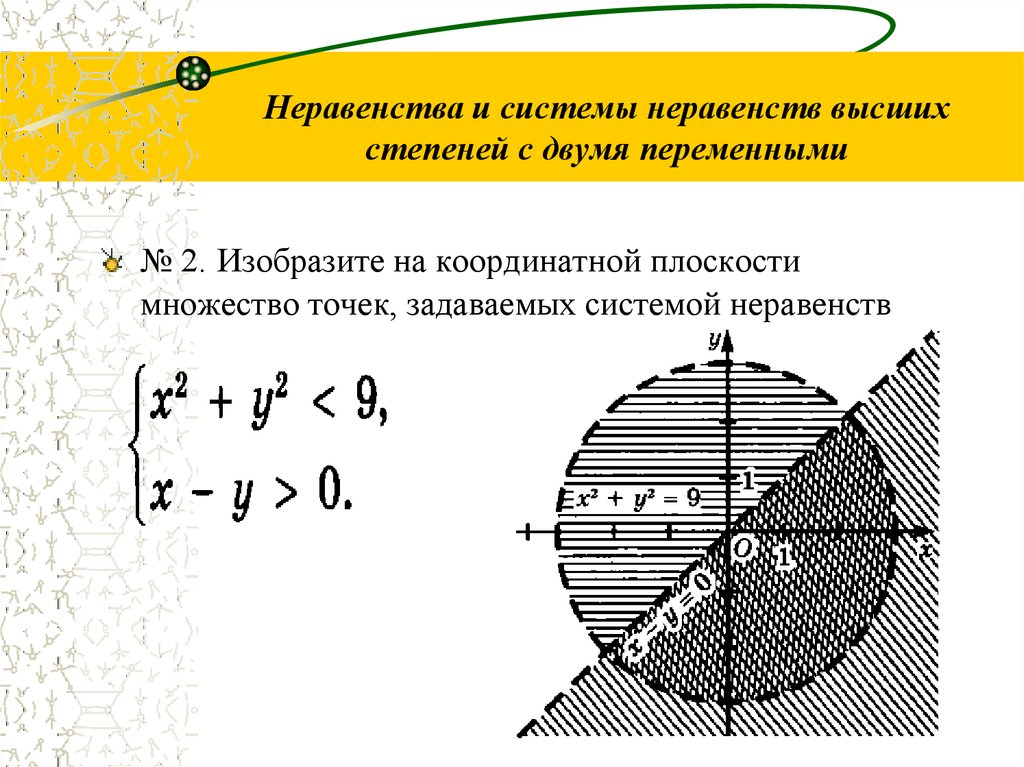
9. Неравенства и системы неравенств высших степеней с двумя переменными

№ 2. Изобразите на координатной плоскости
множество точек, задаваемых системой неравенств

10. Неравенства и системы неравенств высших степеней с двумя переменными

№ 3. Изобразите на координатной плоскости множество точек,
задаваемых системой неравенств
x 2 y 2 4,
2
2
x y 6 x 0.
Преобразуем первое неравенство системы:
x 6x 9 y 9
2
2
( x 3) y 9
2
2

11. Неравенства и системы неравенств высших степеней с двумя переменными

Получим равносильную систему
x 2 y 2 4,
2
2
(
x
3)
y
9.

12. Неравенства и системы неравенств высших степеней с двумя переменными

№ 4. Изобразите на координатной плоскости множество точек,
задаваемых системой неравенств
x y 2,
2
y x 2.
2

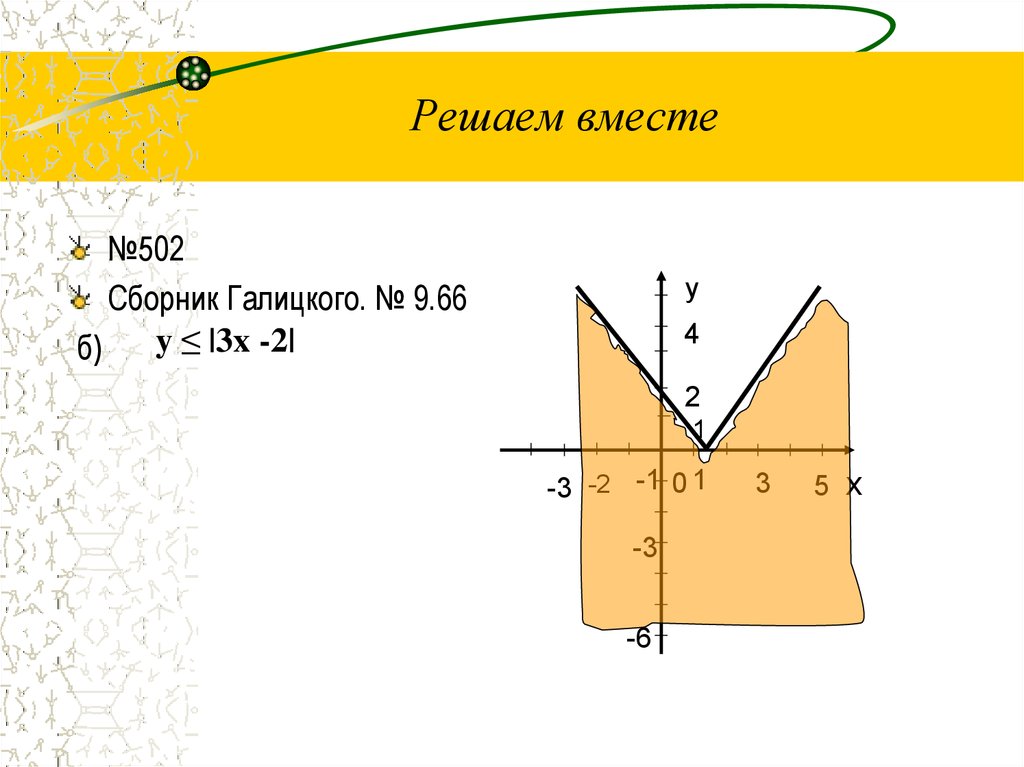
13. Решаем вместе

№502
Сборник Галицкого. № 9.66
y ≤ |3x -2|
б)
у
4
2
1
-3 -2 -1 0 1
-3
-6
3
5 х

14. Решаем вместе

.№ 9.66(в)
у
|y| ≥ 3x - 2
4
2
1
-3 -2 -1 0 1
-3
-6
3
5 х

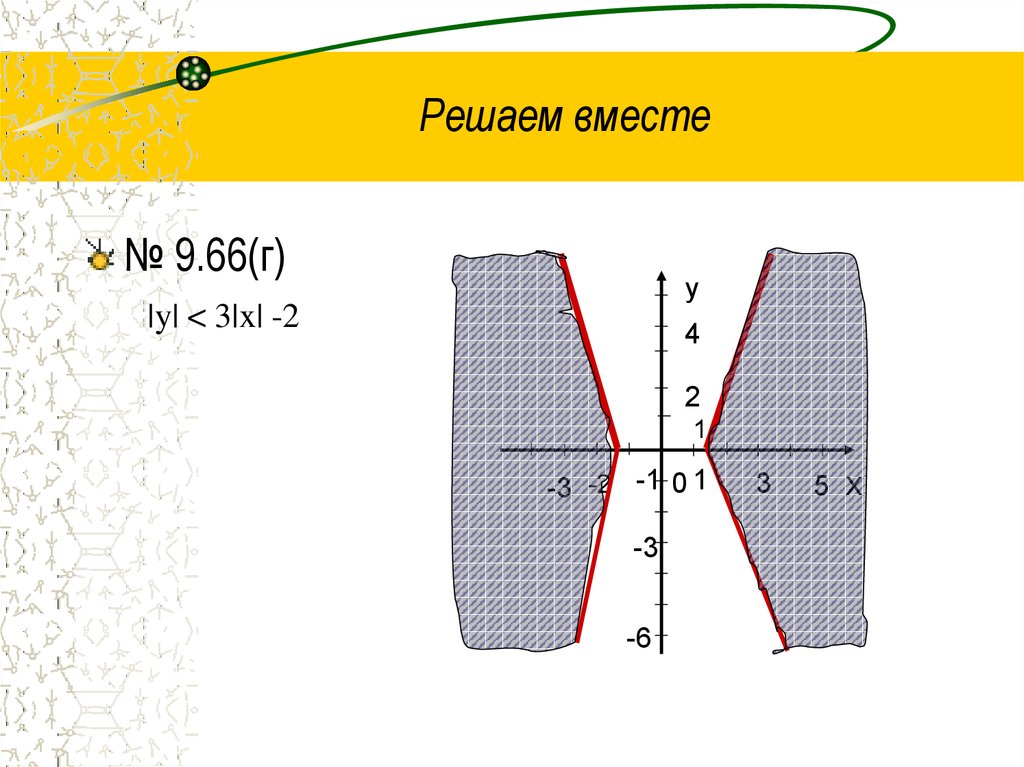
15. Решаем вместе

№ 9.66(г)
у
|y| < 3|x| -2
4
2
1
-3 -2 -1 0 1
-3
-6
3
5 х

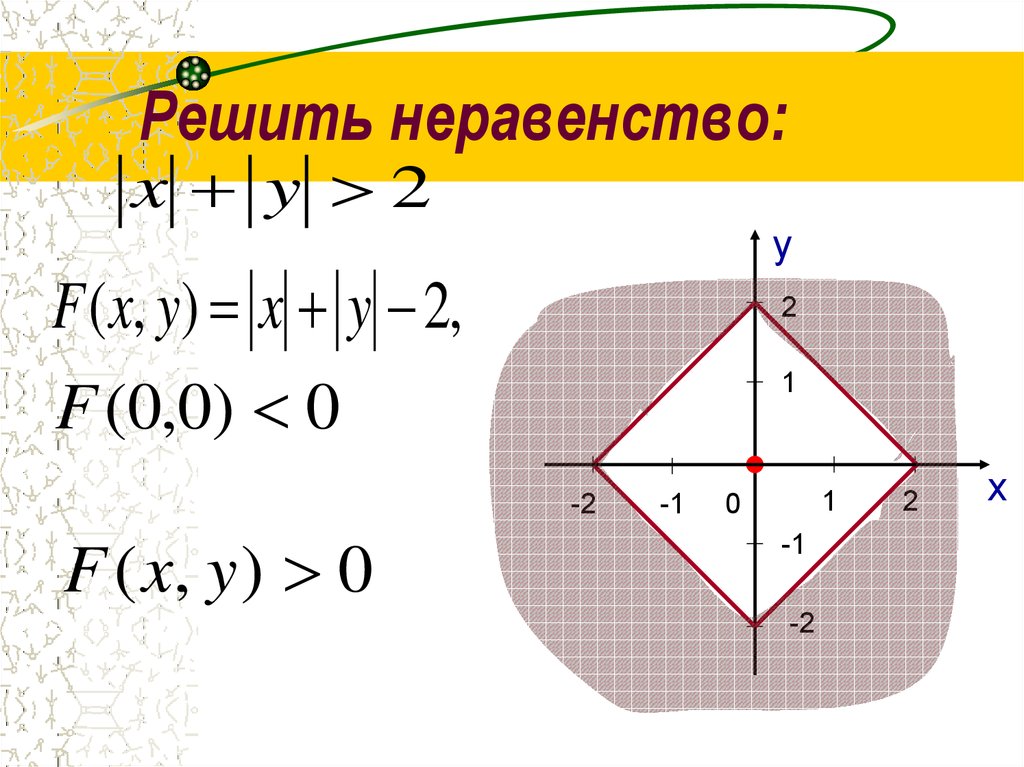
16. Решить неравенство:

x y 2
y
F ( x, y) x y 2,
F (0,0) 0
2
1
-2
F ( x, y ) 0
-1
1
0
-1
-2
2
x

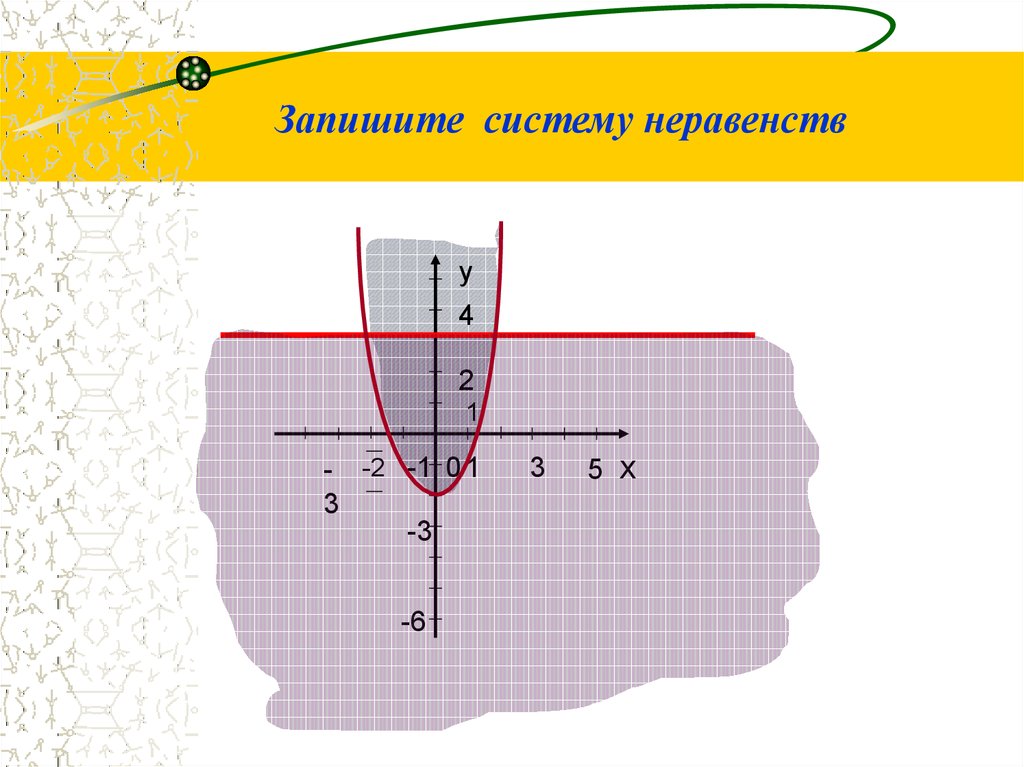
17.

Запишите систему неравенств
у
4
2
1
- -2 -1 0 1
3
-3
-6
3
5 х

18.

Запишите систему неравенств
у
4
2
1
-3 -2
-1 0 1
-3
-6
3
5 х

19. Решение тренировочных упражнений

1) Изобразите на координатной плоскости множество
решений системы:
у х 2 4,
у x 2 1,
у 2,
x 2 y 2 4,
г )
в )
а)
б )
2
х у 2
у 3 х
у 3 х 5
у 4 х
2) Запишите систему неравенств с двумя переменными,
множество решений которой изображено на рисунке
3) Какую фигуру задает множество х у 0,
2 х 4,
решений системы неравенств?
а ) х у 5, б )
1 у 1
Найдите площадь каждой фигуры. х 0.
4) Задайте системой неравенств кольцо,
изображенное на рисунке.
5)Решите систему неравенств
x 2 y 2 2 у,
у 1 х
у
2
0
2
х
у
10
5
0
5
10
х
6)Сколько пар натуральных чисел являются решениями системы неравенств
?
Вычислите сумму всех таких чисел.
05:42
y x 2,
2
2
( x 2) y 4

20. Решение тренировочных упражнений

7) Вычислите площадь фигуры, заданной множеством решений
системы неравенств и найдите наибольшее расстояние между
точками этой фигуры
1 х 3,
2 у 5.
8) При каком значении m система неравенств
имеет только одно решение?
у х 2 m,
y 2 x 2
9)Укажите какие-нибудь значения k и b, при которых система неравенств
задает на координатной плоскости: а) полосу; б) угол.
у 2 х 3,
у kx b

21. Домашнее задание

№503; 9.68 (а, б); 9.69 (а, б);