Similar presentations:
Неравенства с двумя переменными и их системы ( урок - 3 )
1.
Урок 32.
y6
4
2
-6
-4
-2
0
2
-2
-4
x
3. Найдите ошибку!
|2
|
|
|
y
|
|
|
|
|
|
|
|
|
|
|
Найдите ошибку!
( x 1)2 ( y 2)2 4
1
|
|
|
x
4. Определите неравенство
уxy
000
xy – 68
xy
>
4
2
xy 6 0
xy 6 0
1
3
-2 -1 0 1
-3
xy 6 0
-6
3
5
х
5.
Определите неравенствоу
4
x 2 y 2 16
2
x 2 y 2 16
1
-3 -2
-1 0 1
-3
-6
3
5 х
x 2 y 2 16
x 2 y 2 16
6.
Определите знак неравенствау
y
2
1
-3 -2
-1 0 1
-3
3
5
х
?≤
x 2x 1
2
7.
Изображение множества решений системынеравенств с двумя переменными на
координатной плоскости
Множеством решений системы неравенств с двумя
переменными является пересечение множеств решений
неравенств, входящих в систему. На координатной плоскости
множество решений системы неравенств изображается
множеством точек, являющихся общей частью множеств,
представляющих собой решения каждого неравенства
системы.
8.
х 2у 3
у
у = -3
у 3 (прямая )
1. Построим прямую х = 2.
2. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
х =2
О
х 2 (прямая )
х
3. Построим прямую у = -3.
4. Она разбивает плоскость на две
области, выбираем нужную нам
область и наносим штриховку
Решениями данной системы
являются координаты точек
пересечения множеств решений
неравенств системы
(прямой угол)
9.
2 у 3 х 6у 2 х 3
у
2 у 3 х 6 (прямая )
у
6 3х
2
х
0
2
у
3
0
1. Построим прямую 2у + 3х = 6
2. Она разбивает плоскость на две области, выбираем
нужную нам область и наносим штриховку
О
х
у 2 х 3 (прямая )
х
0
2
у 2х 3
у
-3
1
3. Построим прямую у - 2х = -3
4. Она разбивает плоскость на две области, выбираем
нужную нам область и наносим штриховку
Решениями данной системы являются
координаты точек пересечения множеств
решений неравенств системы (угол)
10.
у 2х 1у 2х 1
у
у 2х 1
х
0
1
у
1
3
1. Построим прямую у = 2 х + 1
2. Она разбивает плоскость на две области, выбираем
нужную нам область и наносим штриховку
О
х
у 2х 1
х
0
1
у
-1
1
3. Построим прямую у = 2 х - 1
4. Она разбивает плоскость на две области, выбираем
нужную нам область и наносим штриховку
Решениями данной системы являются
координаты точек пересечения
множеств решений неравенств
системы (полоса)
11.
х2 у 2 12 х у 0
у
х 2 у 2 1 (окружность)
центр (0; 0), R 1
О
х
1. Построим окружность х2 + у2 = 1
2. Она разбивает плоскость на две области,
выбираем нужную нам область и наносим
штриховку
2 х у 0 (прямая )
х
0
1
у 2 х
у
0
-2
3. Построим прямую 2х + у = 0
4. Она разбивает плоскость на две области,
выбираем нужную нам область и наносим
штриховку
Решениями данной системы
являются точки полукруга
12.
у х 2 2 х 1( х 1) 2 ( у 2) 2 1
у
у х 2 2 х 1 (парабола )
у ( х 1) 2 2
О
х
Вершина (1; 2)
1. Построим параболу у = (х - 1)2-2
2. Она разбивает плоскость на две области,
выбираем нужную нам область и наносим
штриховку
( х 1) 2 ( у 2) 2 1 (окружность)
центр (1; 2), R 1
3. Построим окружность (х-1)2+(у+2)2=1
4. Она разбивает плоскость на две области, выбираем
нужную нам область и наносим штриховку
Решениями данной системы являются
точки пересечения множеств решений
неравенств системы
13.
Изобразить множество точек, которыеявляются решениями системы и вычислить
площадь получившейся фигуры
у
х 2 4 х у 2 4 у 0
2
х 2 х у 2 2 у 0
х
О
2 2
2
х2 4х у2 4 у 0
х2 4х 4 4 у2 4 у 4 4 0
х2 4х 4 у2 4 у 4 8
( х 2) 2 ( у 2) 2 ( 2 2 ) 2
R 2 2 R 2
Окр. с 1центром (2; 22) и R 2 2
х S 4 х
уR1 4 у
0R2
2
2
2
2
2 2 у 1 1 02
х2 2х 1 1 у 2
S (2 2 ) ( 2 )
х 2х 1 у2 2 у 1 2
2
12) 2 ( 26) 2
(хS
1
)2 8
(у
Окр. с центром (1; 1) и R 2
14. Решить графически систему неравенств
yx y 4 0,
y 0,
x 0
2
2
2
1
-2
-1
0
1
-1
-2
2
x
15. Неравенства и системы неравенств высших степеней с двумя переменными
№1. Изобразите на координатной плоскости множествоточек, задаваемых системой неравенств
x y 25,
2
2 y x 1 0.
2
2
16. Неравенства и системы неравенств высших степеней с двумя переменными
№ 2. Изобразите на координатной плоскостимножество точек, задаваемых системой неравенств
17. Неравенства и системы неравенств высших степеней с двумя переменными
№ 3. Изобразите на координатной плоскости множествоточек, задаваемых системой неравенств
x 2 y 2 4,
2
2
x y 6 x 0.
Преобразуем второе неравенство системы:
x 6x 9 y 9
2
2
( x 3) y 9
2
2
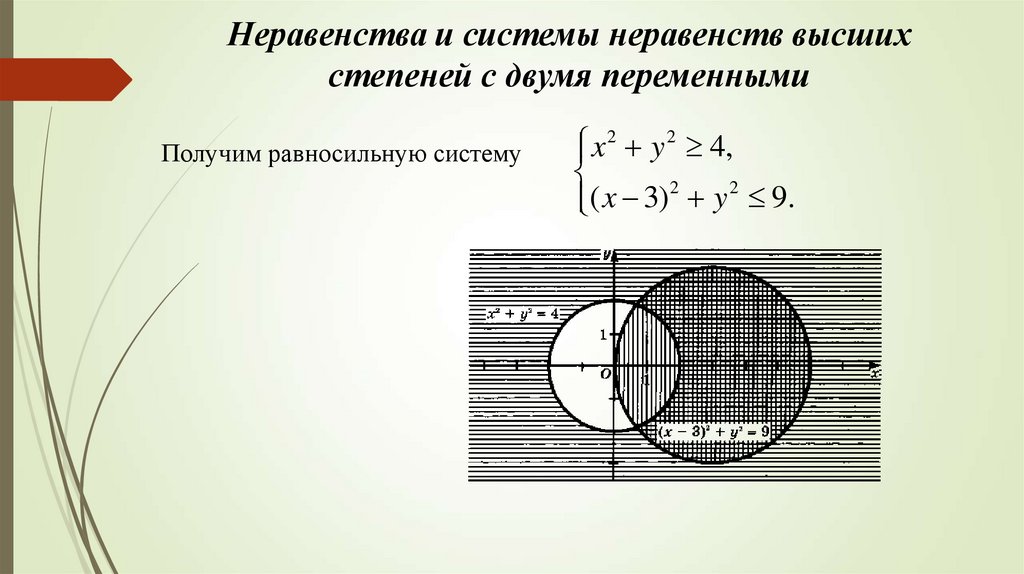
18. Неравенства и системы неравенств высших степеней с двумя переменными
Получим равносильную системуx 2 y 2 4,
2
2
(
x
3)
y
9.
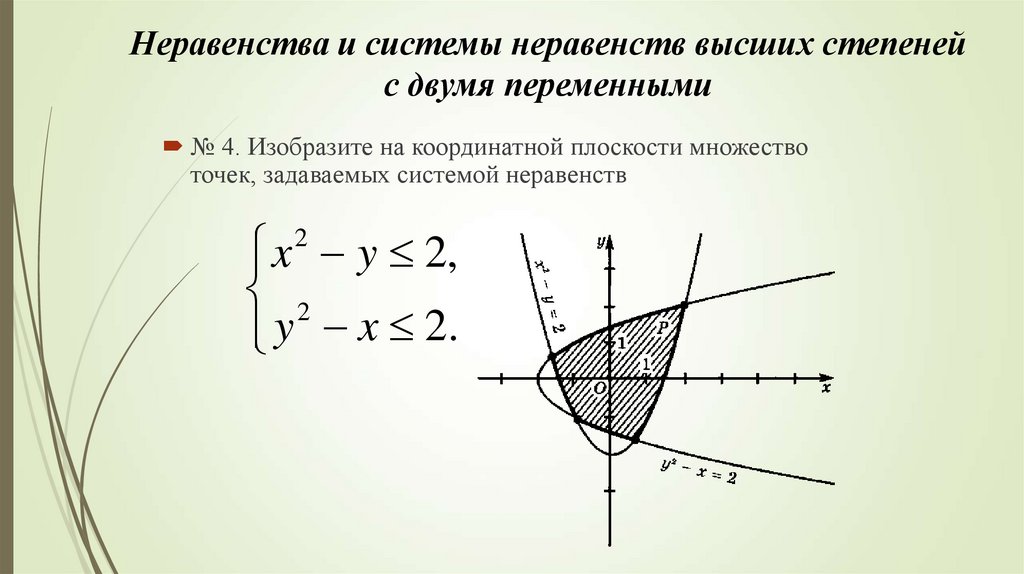
19. Неравенства и системы неравенств высших степеней с двумя переменными
№ 4. Изобразите на координатной плоскости множествоточек, задаваемых системой неравенств
x y 2,
2
y x 2.
2
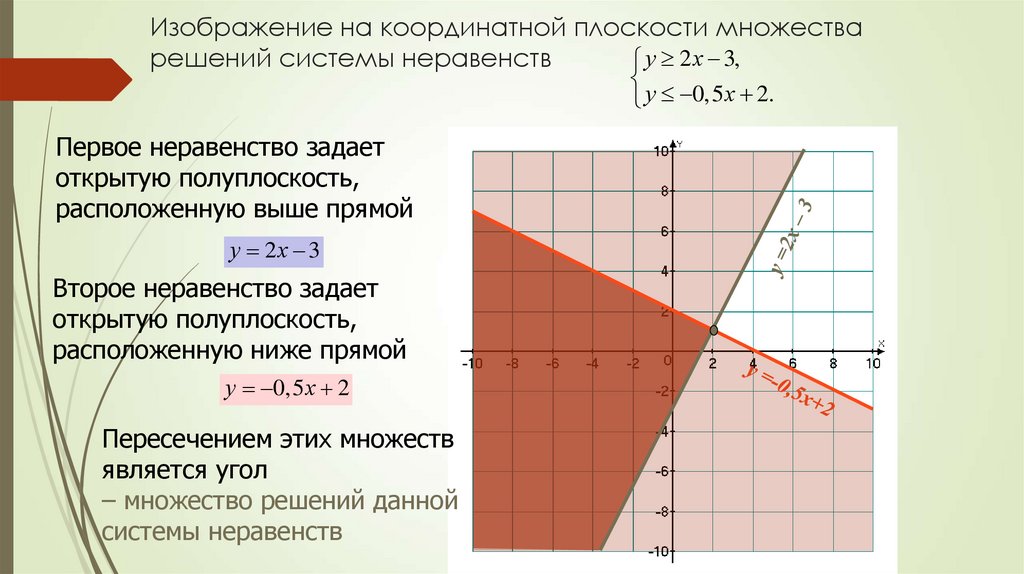
20. Изображение на координатной плоскости множества решений системы неравенств
у 2 х 3,у 0,5 х 2.
Первое неравенство задает
открытую полуплоскость,
расположенную выше прямой
у 2х 3
Второе неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у 0,5 х 2
Пересечением этих множеств
является угол
– множество решений данной
системы неравенств
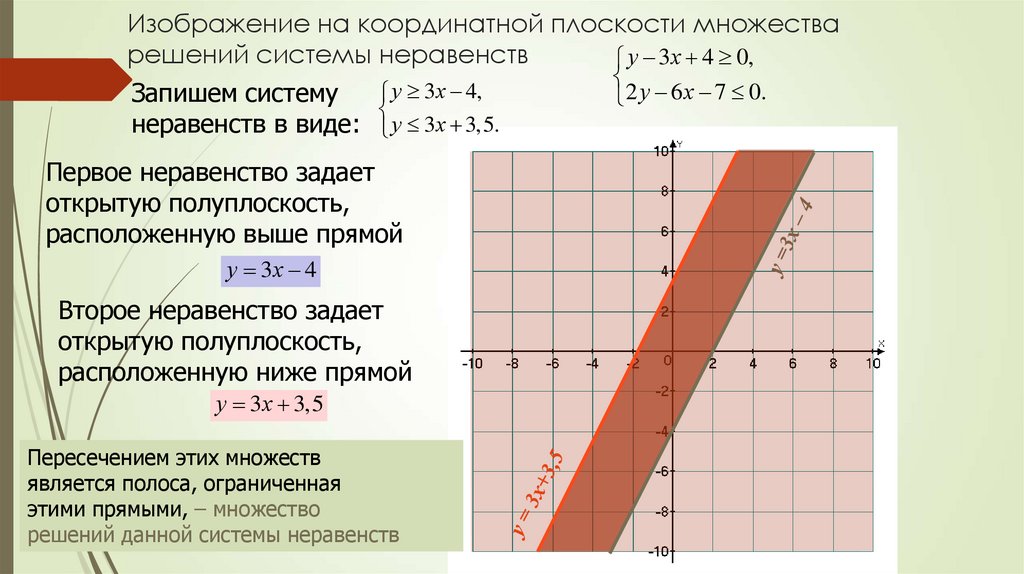
21. Изображение на координатной плоскости множества решений системы неравенств
у 3х 4 0,у
3
х
4,
Запишем систему
2 у 6 х 7 0.
неравенств в виде: у 3х 3,5.
Первое неравенство задает
открытую полуплоскость,
расположенную выше прямой
у 3х 4
Второе неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у 3х 3,5
Пересечением этих множеств
является полоса, ограниченная
этими прямыми, – множество
решений данной системы неравенств
22. Изображение на координатной плоскости множества решений системы неравенств
у 3х 4 0,Запишем систему
неравенств в виде:
у 3х 4,
у 3х 3,5.
Первое неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у 3х 4
Второе неравенство задает
открытую полуплоскость,
расположенную выше прямой
у 3х 3,5
Множество точек, заданное
данной системой неравенств –
пустое множество.
2 у 6 х 7 0.
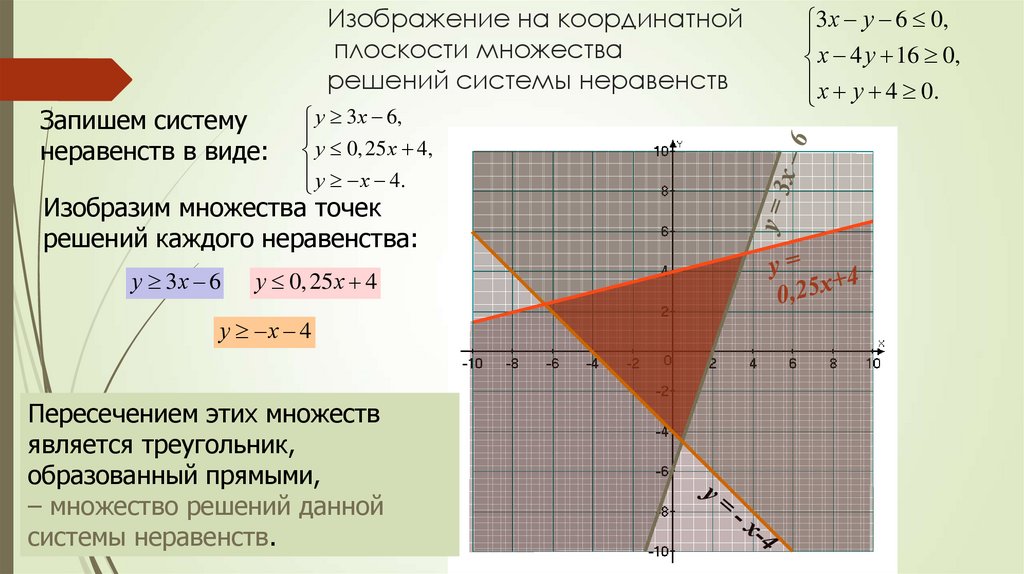
23. Изображение на координатной плоскости множества решений системы неравенств
Запишем системунеравенств в виде:
у 3 х 6,
у 0, 25 х 4,
у х 4.
Изобразим множества точек
решений каждого неравенства:
у 3х 6
у 0, 25 х 4
у х 4
Пересечением этих множеств
является треугольник,
образованный прямыми,
– множество решений данной
системы неравенств.
3 х у 6 0,
х 4 у 16 0,
х у 4 0.
24.
Изображение на координатнойплоскости множества
решений системы неравенств
у x 2 8 х 12,
Запишем систему
неравенств в виде:
у х 2.
у x 2 8 x 12,
y х 2 0.
у х 2 8х 12
Изобразим множества точек
решений каждого неравенства:
у x 2 8х 12
у х 2
Данная система неравенств
задает ту из образовавшихся
областей, которая расположена
выше параболы и ниже прямой.
у х 2
25.
Изображение на координатнойплоскости множества
решений системы неравенств
ху 5 0,
2
2
х
у
36.
Изобразим множества точек
решений каждого неравенства:
ху 5 0
х2 у 2 36
х2 у 2 36
Данная система задает
две области, образовавшиеся
при пересечении множеств
решений ее неравенств.
ху 5 0




















 mathematics
mathematics








