Similar presentations:
Системы неравенств с двумя переменными
1. Системы неравенств с двумя переменными
Демонстрационный материал11 класс
Все права защищены. Copyright с 2010. http://www.mathvaz.ru
Copyright с
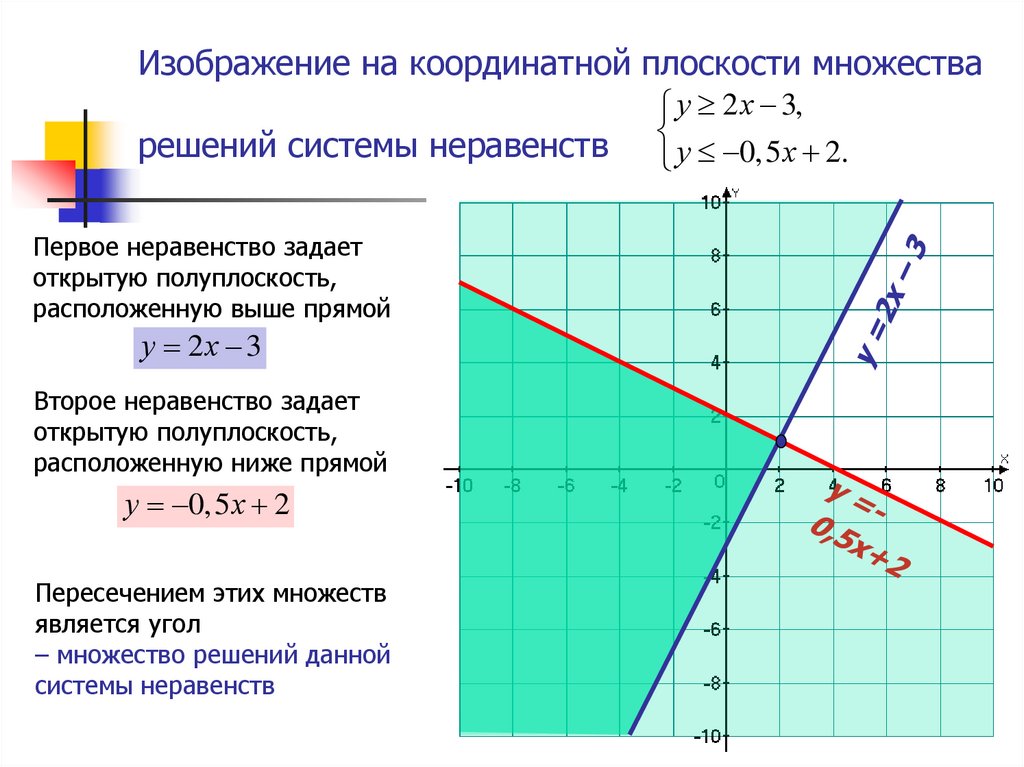
2. Изображение на координатной плоскости множества решений системы неравенств
Первое неравенство задаетоткрытую полуплоскость,
расположенную выше прямой
у 2х 3
Второе неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у 0,5 х 2
Пересечением этих множеств
является угол
– множество решений данной
системы неравенств
у 2 х 3,
у 0,5 х 2.
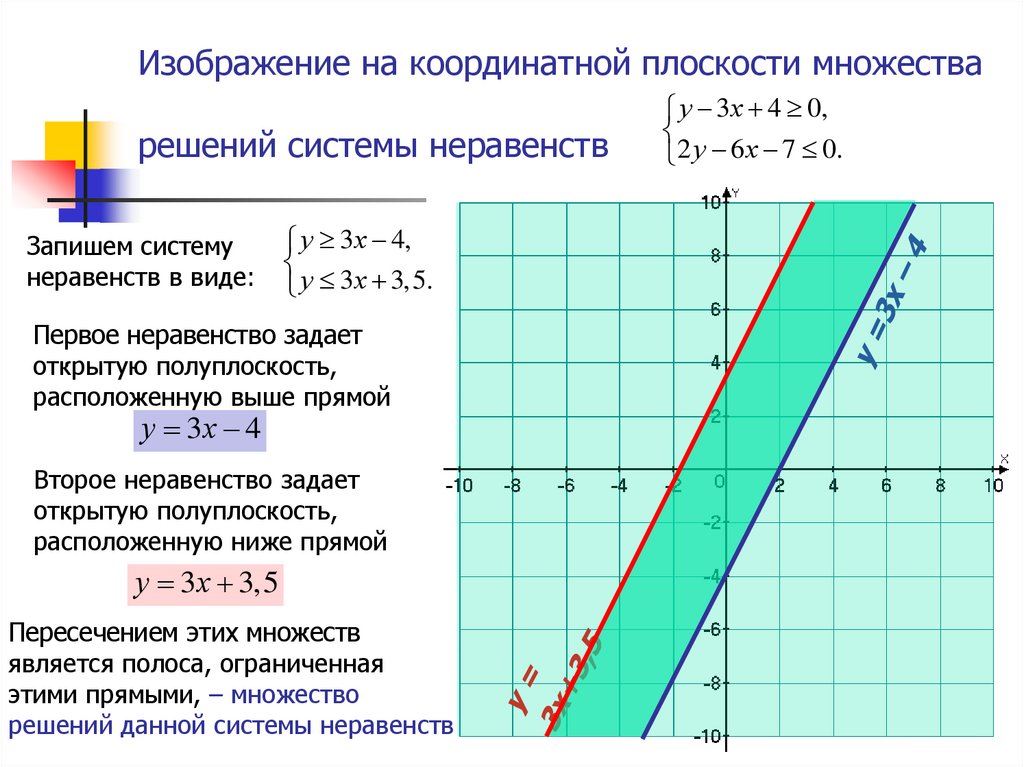
3. Изображение на координатной плоскости множества решений системы неравенств
Запишем системунеравенств в виде:
у 3х 4,
у 3х 3,5.
Первое неравенство задает
открытую полуплоскость,
расположенную выше прямой
у 3х 4
Второе неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у 3х 3,5
Пересечением этих множеств
является полоса, ограниченная
этими прямыми, – множество
решений данной системы неравенств
у 3х 4 0,
2 у 6 х 7 0.
4. Изображение на координатной плоскости множества решений системы неравенств
Запишем системунеравенств в виде:
у 3х 4,
у 3х 3,5.
Первое неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у 3х 4
Второе неравенство задает
открытую полуплоскость,
расположенную выше прямой
у 3х 3,5
Множество точек, заданное
данной системой неравенств –
пустое множество.
у 3х 4 0,
2 у 6 х 7 0.
5. Изображение на координатной плоскости множества решений системы неравенств
у 3 х 6,Запишем систему
у 0, 25 х 4,
неравенств в виде:
у х 4.
Изобразим множества точек
решений каждого неравенства:
у 3х 6
у 0, 25 х 4
у х 4
Пересечением этих множеств
является треугольник,
образованный прямыми,
– множество решений данной
системы неравенств.
3 х у 6 0,
х 4 у 16 0,
х у 4 0.
6.
Изображение на координатнойплоскости множества
решений системы неравенств
Запишем систему у x 8 х 12,
неравенств в виде:
у х 2.
2
у x 2 8 x 12,
y х 2 0.
у х 2 8х 12
Изобразим множества точек
решений каждого неравенства:
у x 2 8х 12
у х 2
Данная система неравенств задает
ту из образовавшихся областей,
которая расположена выше
параболы и ниже прямой.
у х 2
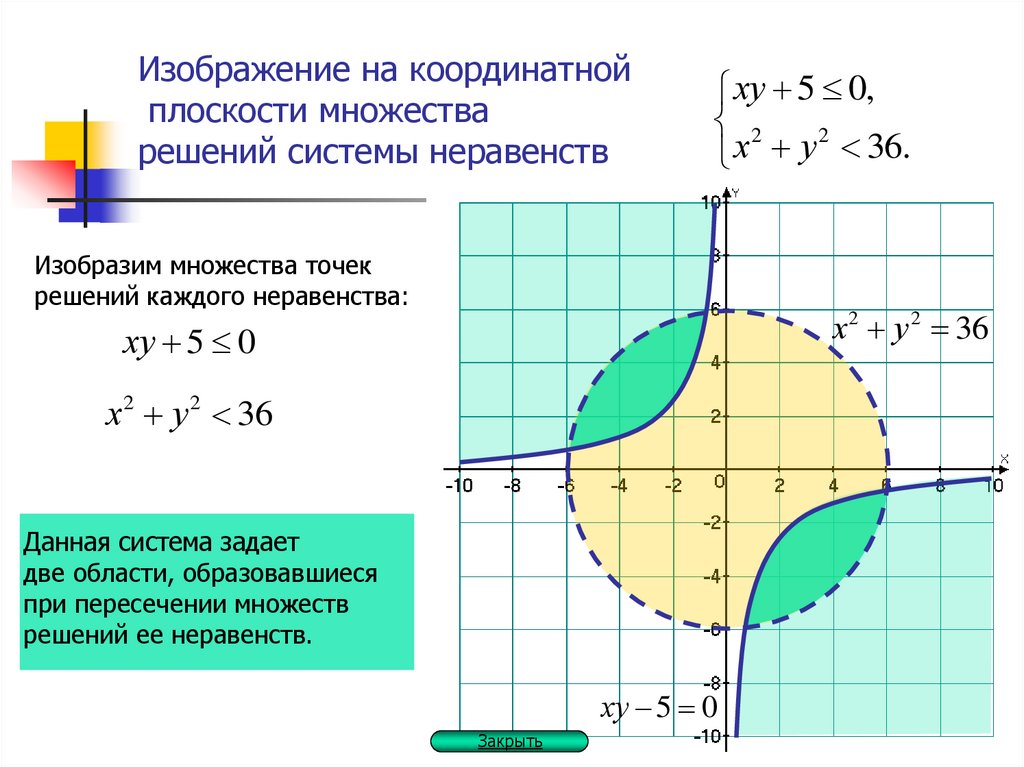
7.
Изображение на координатнойплоскости множества
решений системы неравенств
ху 5 0,
2
2
х
у
36.
Изобразим множества точек
решений каждого неравенства:
х2 у 2 36
ху 5 0
х2 у 2 36
Данная система задает
две области, образовавшиеся
при пересечении множеств
решений ее неравенств.
ху 5 0
Закрыть




 mathematics
mathematics








