Similar presentations:
Решение квадратных уравнений. 8 класс
1.
МОУ БСОШ №2«Образовательный центр.»
Коростина О.В.
2.
Тема урокаРЕШЕНИЕ
КВАДРАТНЫХ
УРАВНЕНИЙ
3. Цель урока:
• Закрепить решения квадратных и биквадратныхуравнений, используя алгоритм решения.
4. Ход урока
Проверка домашнего заданияУстные упражнения
Закрепление изученного
Выполнение теста
Итог урока
Получение отметок
Домашнее задание
5.
• Что называется уравнением?• Какие вы знаете уравнения?
• Какое уравнение называется
квадратным?
• Как решаются квадратные уравнения?
• Как найти дискриминант?
• Д=b2 – 4ac
• Сколько корней имеет квадратное
уравнение, если:
• Д>0
• D<0
• D=0
6.
• Как найти эти корни?в Д
х1, 2
2а
• Какое уравнение называется биквадратным?
• Как решаются биквадратные уравнения?
• Ах2+Вх+С=А(х – х1)(х - х2)
7.
•Х2 =9•Х2 = -25
•Х2 – 4 = 0
•2х2+32 = 0
•2х = 128
•х1 = 3, х2 = -3
•Нет решений
•х1 = 2, х2 = -2
•Нет решений
•Х =64
8. 1-ый уч –ся: 1) х4 – 9х2 + 20=0
2 –ой уч-ся:2) х4 – 11х2 + 18 =0
Класс: № 461 (1) Сократите дробь
2х2 -10х +12
х2 - 7х + 12
9. 2х2 - 10х+12 = 2(х - 3)(х-2) х2 - 7х+ 12 1(х -4)(х – 3)
2
2х
2х2 -10х +12 =0
а=2, в=-10, с=12;
Д=в2-4ас;
Д=(-10)2 – 4*2*12;
Д=100 - 96;
Д=4
х1 = 3; х2 = 2
х2 - 7х + 12=0
• а=1, в= -7, с= 12;
• Д=в2-4ас;
• Д=(-7)2 – 4*1*12;
• Д=49 - 48;
• Д=1
• х1 = 4; х2 = 3
- 10х+12 = 2(х - 3)(х-2)
2
х - 7х+ 12
1(х -4)(х – 3)
10. Решите биквадратное уравнение:
•х4 + 4х2 – 45 =0•х2=у
у2 + 4у – 45 = 0
Д= 196
у1=-9; у2=5
•х2= -9 ;
•Нет
Решений
х2=5
х1=√5
х2= -√5
11. Тест I вариант II вариант
ТестI вариант
• 2х2 + 3х + 1=0
II вариант
2х2 – 3х + 1=0
• 1.Выпишите коэффициенты
• а=
• в=
• с=
а=
в=
с=
• 2.Найдите дискриминант
• 1) 4; 2) 1; 3) 25.
• 3.Найдите корни уравнения:
• 1) 1;-1/2.
2) -1; -1/2 .
3) 1;1/2.








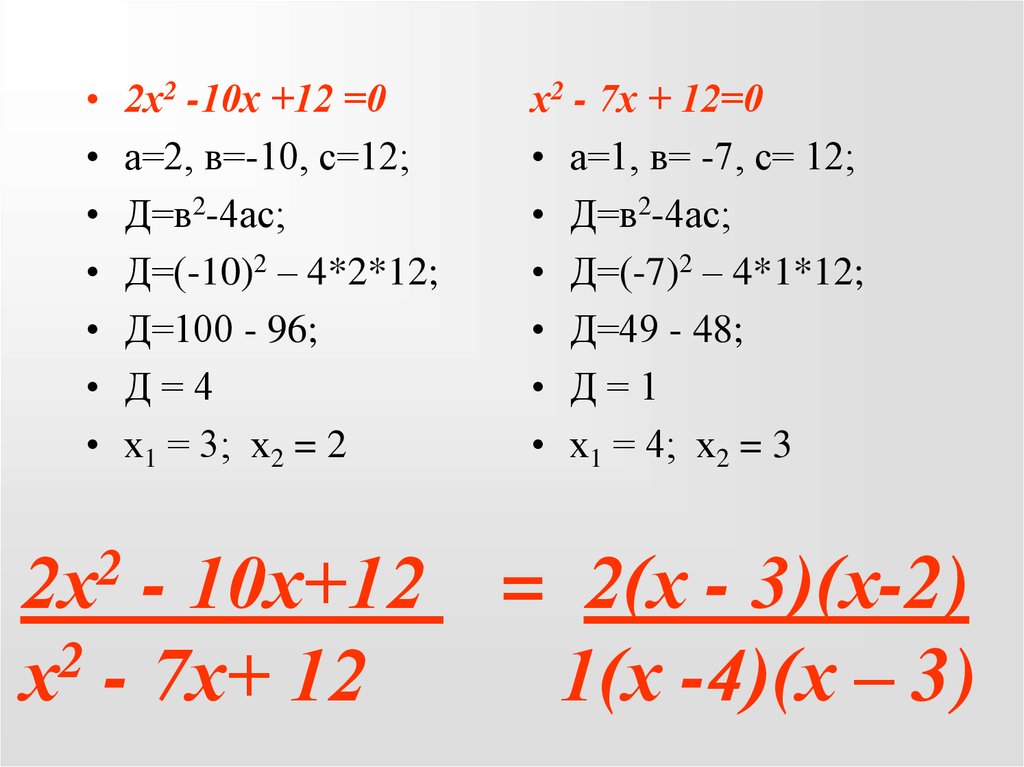



 mathematics
mathematics








