Решение тригонометрических уравнений различными способами

1. Решение тригонометрических уравнений различными способами

2.

Решите уравнение sin x – cos x = 1
Решение:
1. Преобразуем данное уравнение к виду
sin x – ( 1 + cos x) = 0.
2. Применяя формулы половинного и двойного аргумента
x
1 cos x 2 cos ,
2
2
x
x
sin x 2 sin cos ,
2
2
получим:
x
x
2 x
2 sin cos 2 cos 0;
2
2
2
x
x
x
cos sin cos 0
2 2
2

3.

3. Произведение равно нулю, если хотя бы один из
множителей равен нулю, а остальные при этом не
теряют смысла, поэтому
x
x
x
cos sin cos 0;
2
2
2
x
cos 2 0,
sin x cos x 0;
2
2
x
x
x
cos 0;
sin cos 0
2
2
2
x
однородное уравнение
k ;
2 2
I степени
x
x 2 k ; k ; Делим обе его части на cos
2

4.

Получим
x
tg 1 0;
2
x
tg 1;
2
x
n;
2 4
x
Ответ : x
2 n, n
2
x 2 k , k .
2
2 n; n .

5.

x 2 k , k ,
x 2 n, n ,
2
x 2 m, m ,
x 2 l , l .
2
у
2
2 k
2 m
Ответ : x
2 k , k
2
x 2 n, n .
х
0
Первое и четвертое
решения –
посторонние
2 n
2
2 l

6.

Убедимся, что решения данного уравнения
x
4
( 1)
k
4
k
И
x 2 k ,
x 2 n;
2
совпадают
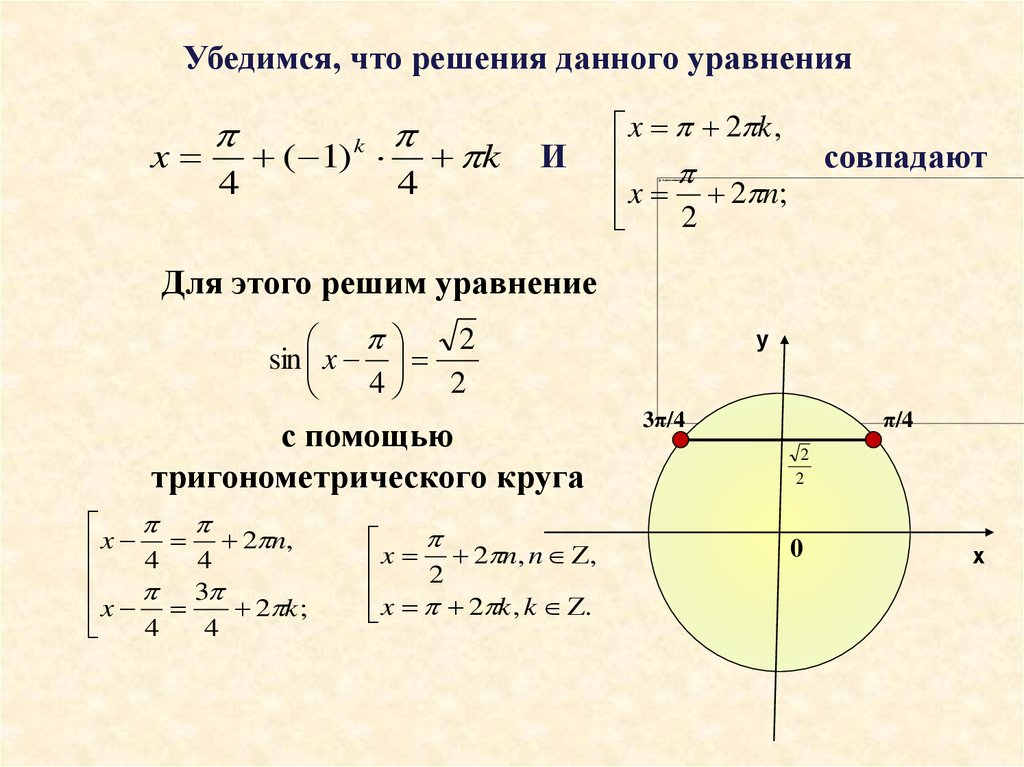
Для этого решим уравнение
2
sin x
4 2
с помощью
тригонометрического круга
x
2 n,
4
4
x 3 2 k ;
4
4
x
2 n, n ,
2
x 2 k , k .
у
π/4
3π/4
2
2
0
х

7.

Решите уравнение sin x – cos x = 1
Решение:
1. Преобразуем данное уравнение к виду
sin x = 1 + cos x.
2. Построим графики функций y=sin x и y=1 + cos x
в одной системе координат.
3. Найдем абсциссы точек пересечения графиков
функций.

8.

sin x – cos x = 1
2,5
у
y=sin(x)
2
y=1+cos(x)
1,5
x
1
0,5
3
2
3
2
2
0
-0,5
-1
-1,5
Ответ : x
2 n, n
2
x 2 k , k .
2
2 n, n
x 2 k , k .
3
2
2
2 5
2
3
х