Similar presentations:
Методы решения различных уравнений
1. Методы решения различных уравнений
Тема урокаМетоды решения
различных
уравнений
Кузнецова Татьяна Алексеевна, учитель высшей квалификационной
категории МБОУ «Берёзовская СОШ»,
Шилова Анастасия Александровна, учитель первой квалификационной
категории МБОУ «Берёзовская СОШ»
2.
Не для школы, а дляжизни мы учимся.
/античный афоризм/
3.
I. Решите устно4.
По графикам квадратичной функцииу=ах2 + в х +с
расскажите о квадратном уравнении
ах2 + в х +с =0
5.
2)4)
6.
№ 1 Выясните, имеет ли корниуравнение
х2 + 2 √3 х - х = - 1,5
7.
Решение:х2 + 2 √3 х - х = - 1,5
х2 + (2 √3 - 1)х + 1,5=0
Д= (2 √3 - 1)2 – 6 = 12 – 4 √3 + 1 – 6
= 7 – 4 √3 = √49– √48 > 0
Ответ: уравнение имеет два корня.
8.
№ 2 При каких значенияхпараметра k уравнение
3х2 + 4 х +k=0
не имеет корней
9.
Решение:3х2+ 4 х +k=0
Д = 16 - 12 k
16 - 12 k < 0
- 12 k < - 16
16
k > 12
4
k>
3
1
k>1
3
1
Ответ: уравнение не имеет корней при k > 1
3
10.
№ 3 Найдите все целые значенияm, при которых уравнение
mх2 - 5х + 0,25 m = 0
имеет два корня
11.
Решение:mх2 - 5х + 0,25m = 0
Д = 25 - 4m • 0,25m = 25 – m2
25 – m2 > 0
m2 – 25 < 0
(m – 5) (m + 5) < 0
m=5 m=–5
+
–
-5
+
m
5
-5<m<5
Ответ: при m равных -4; - 3; - 2; - 1; 0; 1; 2; 3; 4 уравнение
имеет целые корни
12.
№4 Проверьте решение уравнения2х3 – 6х2 – 4х + 12 = 0
(2х3 – 6х2) + (– 4х + 12) = 0
2х2( х – 3 ) – 4 ( х – 3) = 0
х2( х – 3 ) – 2 ( х – 3) = 0
( х – 3 ) ( х2 – 2) = 0
( х – 3 )(х – 2)( х + 2)=0
х – 3 =0 или х – 2 = 0 или х + 2 = 0
х=3
х=2
х=–2
Ответ: – 2; 2; 3
13.
№ 5 Решите уравнениеметодом разложения на
множители
х5 – 3х4 + 2х3 – 6х2 – 3х + 9 = 0
14.
Решение:х5 – 3х4 + 2х3 – 6х2 – 3х + 9 = 0
(х5 – 3х4) +( 2х3 – 6х2) – (3х – 9) = 0
х4(х – 3) + 2х2(х – 3) - 3(х – 3) = 0
(х – 3) (х4+ 2х2- 3) = 0
х = 3 или х4+ 2х2- 3 = 0
х2= t > 0
t2 + 2t – 3 = 0
t1 t 2 2 t1 = -3 – не удовлетворяет условию
t t 3 t2 = 1
1
2
x2 = 1
x = ±1
Ответ: 3; -1; 1
15.
№6 Решите уравнение методомзамены переменной
(х3 + 1)2 – 2(х3 + 1) – 63= 0
16.
Решение:(х3 + 1)2 – 2(х3 + 1) – 63= 0
х3+1 =t:
t2 – 2t – 63 = 0
t1 t 2 2
t1 t 2 63
x3 + 1 = 9
x3 = 8
x=2
t1 = 9
t2 = -7
x3 + 1 = -7
x3 = -8
x = -2
Ответ: 2; -2.
17.
№7 Решите уравнение методомзамены переменной
x x 5
3x
2
4 0
x
x x 5
2
18.
Решение:x2 x 5
3x
2
4 0
x
x x 5
x2 x 5
t
x
3
t 4 0
t
2
t2 – 4t + 3 =0
t1 t 2 4
t1 t 2 3
t1 = 3
t2 = 1
19.
x2 x 53
x
x2 x 5
1
x
x2 – x – 5 – 3x = 0
x2 – 4x – 5 = 0
x2 – x – 5 – x = 0
x2 – 2x – 5 = 0
x1 x2 4
x1 x2 5
Д = 4 + 20 =24
х1 = -1
х2 = 5
Ответ: -1; 5; 1 6 ; 1 6
x 3, 4
2 24 2 2 6
1 6
2
2
20.
Задание на дом:1. Выясните, имеет ли корни
уравнение
х2 + 2 х √3 + 14 = - 4х
2. Решите уравнение методом деления
многочлена на многочлен
х5 – 3х4 + 2х3 – 6х2 – 3х + 9 = 0
3.При каких значениях k уравнение
имеет два различных корня
2х3 – 12х2 + kх = 0


















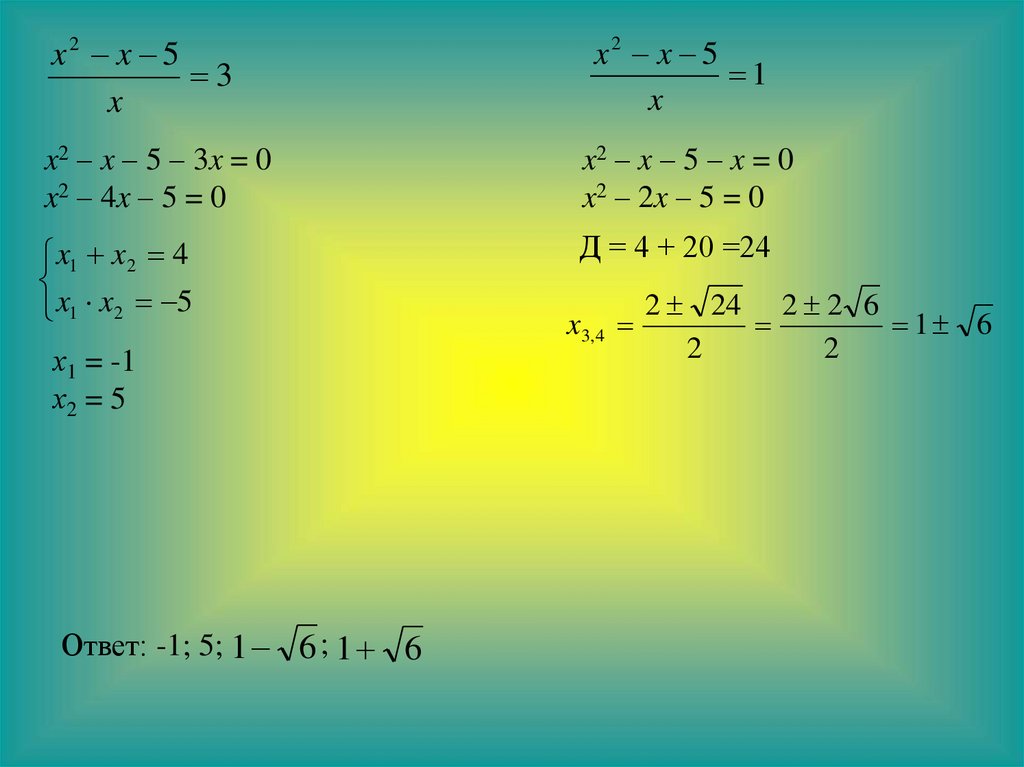


 mathematics
mathematics








