Similar presentations:
Способы решения тригонометрических уравнений
1.
Тема: «Способы решениятригонометрических уравнений»
Алгебра 10 класс
2.
Знать:Уметь:
2.
2.
1.
3.
4.
Свойства
тригонометрических
функций.
Определения обратных
тригонометрических
функций.
Формулы тригонометрии.
Формулы решения
простейших
тригонометрических
уравнений.
1.
3.
4.
Вычислять значения
тригонометрических
функций.
Вычислять значения
обратных
тригонометрических
функций.
Решать простейшие
тригонометрические
уравнения.
Выполнять тождественные
преобразования выражений.
3.
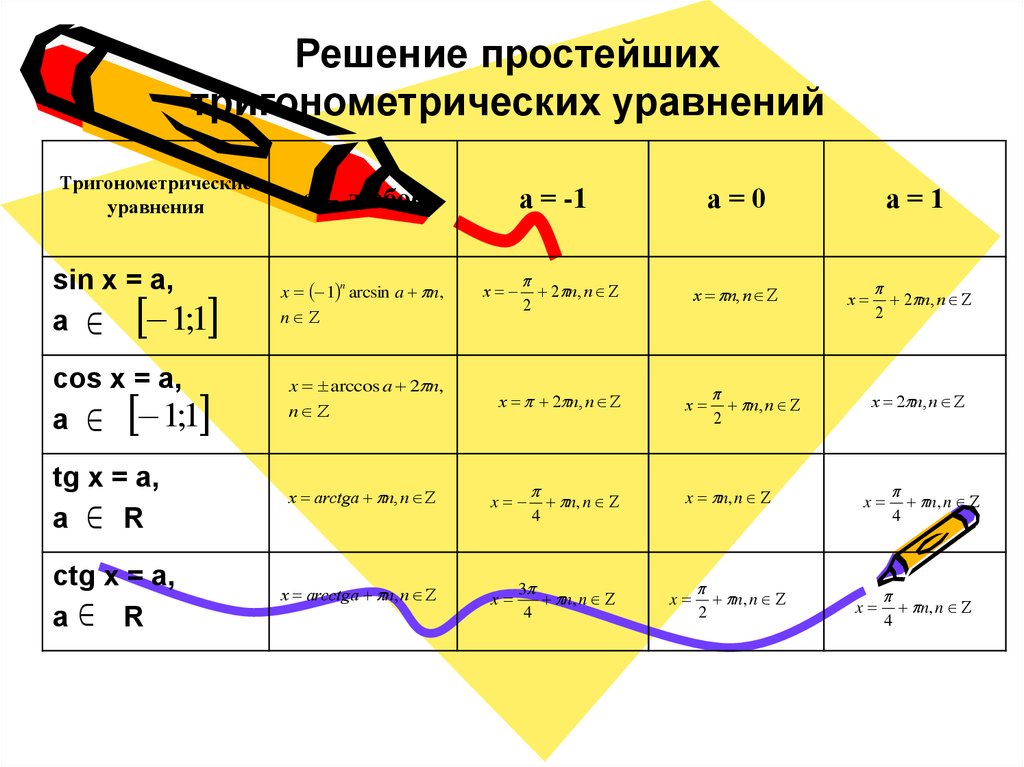
Решение простейшихтригонометрических уравнений
Тригонометрические
уравнения
sin x = a,
1;1
a
cos x = a,
1;1
a
tg x = a,
a
R
ctg x = a,
a
R
а – любое
x 1 arcsin a n,
n
а = -1
x
n
x arccos a 2 n,
n
x arctga n, n
x arсctga n, n
2
2 n, n
x 2 n, n
x
x
а=0
4
n, n
3
n, n
4
x n, n
x
2
n, n
x n, n
x
2
n, n
а=1
x
2 n, n
2
x 2 n, n
x
x
4
4
n, n
n, n
4.
2 sin 2 x 1x
tg ( ) 1
5
2
2 cos(
3
ctg (3 x
2 x) 1
10
) 1 0
5.
1) 2 sin2
x sin x 1 0
2) 2 cos 2 x 5 sin x 4 0
3)tgx 3ctgx 4
sin x
4)
0
1 cos x
5) 2 sin 2 x sin x 0
6) 2 sin 3 x 5 cos 3 x 0
7) sin
2
8) 2 sin
x 2 sin x cos x 3 cos 2 x 0
2
x 2 sin
9) sin x
2
x 2 sin
3 cos x 1
10)3 cos x 4 sin x 5
2
3x 1
6. Методы решения тригонометрических уравнений
Разложение на множители
Сведение к алгебраическому уравнению
Введение вспомогательного угла
Универсальная подстановка
Сведение к однородному уравнению
Использование формул преобразования
суммы в произведение и обратно
Применение формул понижения степени
Обращение к условию равенства
одноименных тригонометрических функций
Использование свойства ограниченности
функций (метод оценки)
7.
Знать:1.
Способы решения
тригонометрических
уравнений:
сведения к квадратному
уравнению
разложения на
множители
понижения степени.
однородные уравнения
введения
вспомогательного угла.
Уметь:
1.
2.
Классифицировать
тригонометрические
уравнения по способу
решения.
Решать тригонометрические
уравнения следующими
способами:
способом сведения к
квадратному уравнению
способом разложения на
множители
способом понижения
степени.
однородные уравнения.
способом введения
вспомогательного угла.
8. Лейбниц
«Метод решения хорош, если с самогоначала мы можем предвидеть – и
впоследствии подтвердить это, что, следуя этому методу, мы
достигнем цели.»
Лейбниц
9. Сведения к квадратному уравнению
2 sin 2 x sin x 1 0Пусть a = sin x
2a 2 a 1 0
1
a1 ; a2 1
2
2) sin x 1
1
1) sin x
2
1
x ( 1) arcsin
k , k Z ;
2
k
x ( 1) k
6
x
2
2 n, n Z
k , k Z
Ответ: x ( 1)
k
6
k , k Z , x
2
2 n, n Z .
10. Сведения к квадратному уравнению
2 cos 2 x 5 sin x 4 0cos 2 x 1 sin
2
x
2(1 sin
2
x ) 5 sin x 4 0
2 2 sin
2
x 5 sin x 4 0
2 sin
x 5 sin x 2 0
2 sin
2
x 5 sin x 2 0
2
Пусть a = sin x
2 a 2 5a 2 0
a1
1
1) sin x
2
6
2) sin x 2
уравнение решения не имеет, так как
x ( 1) k arcsin
x ( 1) k
1
; a2 2
2
1
k , k Z ;
2
sin x 1
k , k Z
Ответ:
x ( 1) k
6
k , k Z
11. Сведения к квадратному уравнению
tgx 3ctgx 4tgx * ctgx 1, tgx
1
ctgx
1
3ctgx 4 * ctgx
ctgx
1 3ctg 2 x 4ctgx
3ctg 2 x 4ctgx 1 0
Пусть a = ctg x
3a 2 4a 1 0
a1
1
1)ctgx
3
1
; a2 1
3
Выполним обратную замену
2)ctgx 1
1
x
n, n Z
x arcctg n, n Z ;
4
3
1
x
n, n Z
x
arcctg
n
,
n
Z
;
Ответ:
4
3
12. Алгоритм решения тригонометрических уравнений.
1. Привести уравнение к квадратному, относительнотригонометрических функций, применяя
тригонометрические тождества.
2. Ввести новую переменную.
3. Записать данное уравнение, используя эту
переменную.
4. Найти корни полученного квадратного уравнения.
5. Перейти от новой переменной к первоначальной.
6. Решить простейшие тригонометрические уравнения.
7. Записать ответ.
13. Разложения на множители
2 sin 2x sin x 0sin 2x 2sin x cos x
4sin x cos x sin x 0
sin x( 4 cos x 1) 0
sin x 0
x n, n Z
Ответ:
4 cos x 1 0
4 cos x 1
1
cos x
4
1
x arccos( ) 2 k , k Z
4
1
x ( arccos ) 2 k , k Z
4
1
x n, n Z , x ( arccos 4 ) 2 k , k Z .
14.
sin 2 x 3 sin x cos xsin 2 x 3 sin x cos x 0
sin x sin x 3 cos x 0
sin x 0
x k , k z
или
sin x 3 cos x 0
15. Однородные уравнения
Первой степени:a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно не равны нулю, то разделим обе
части уравнения на cosx (или на sinx). Получим: простое
уравнение
a∙tgx + b = 0 или tgx = m.
Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x. Получим квадратное
уравнение:
a∙tg²x + b∙tgx + c = 0.
16.
sin 2 x 3 sin x cos xsin 2 x 3 sin x cos x 0
sin x sin x 3 cos x 0
sin x 0
x k , k z
или
sin x 3 cos x 0
( cos x 0
tgx 3 0
tgx 3
x arctg 3 n, n z
Ответ : x k , k z; x arctg 3 n, n z
17. Однородные уравнения
6 sin x 3sin x cos x cos x 12
2
cos x sin 1
2
2
6 sin x 3sin x cos x cos x cos x sin x
2
2
2
2
6 sin 2 x 3sin x cos x cos 2 x cos 2 x sin 2 x 0
5 sin x 3sin x cos x 2 cos x 0 cos x
2
2
5 sin 2 x 3sin x * cos x 2 cos 2 x
0
2
2
2
cos x
cos x
cos x
5tg 2 x 3tgx 2 0
2
18. Однородные уравнения
5tg x 3tgx 2 02
Пусть a = tg x
5a 2 3a 2 0
a1 0,4; a2 1
1)tgx 1
x
4
k , k Z
Ответ: x
2)tgx 0,4
x arctg ( 0,4) n, n Z
x arctg 0,4 n, n Z
4
k , k Z , x arctg 0,4 n, n Z
19. Метод понижения степени
2 sin 2 x 2 sin 2 2 x 2 sin 2 3x 1x 1 cos x
x 1 cos x
; cos 2
2
2
2
2
1 cos 2 x
1 cos 4 x
1 cos 6 x
2*
2*
2*
1
2
2
2
1 cos 2 x (1 cos 4 x) 1 cos 6 x 1
sin 2
1 cos 2 x 1 cos 4 x 1 cos 6 x 1
cos 4 x cos 2 x cos 6 x 0
cos 4 x (cos 2 x cos 6 x) 0
cos cos 2 cos
2
cos
2
20. Метод понижения степени
cos 4x 2 cos 4x cos 2x 0cos 4 x(1 2 cos 2 x ) 0
1 2 cos 2x 0
cos 4 x 0
4x
x
2
8
n, n Z
n
4
, n Z
2 cos 2 x 1
1
cos 2 x
2
1
2 x arccos 2 k , k Z
2
2x
x
Ответ:
x
8
n
4
, n Z,
x
6
3
6
2 k , k Z
k , k Z
k , k Z
21.
Метод понижения степени2 sin 2 x cos 4 x 0
1
1 cos 2 x cos 2 2 x 0
2
1 cos 2 x cos 2 2 x sin 2 2 x 0
2
cos 2 2 x cos 2 x cos 2 2 x 0
2 cos 2 2 x cos 2 x 0
cos 2 x 2 cos 2 x 1 0
1) cos 2 x 0
2x
x
2
4
или
1
cos2 x
2
k , k Z
k
2
2) 2 cos 2 x 1 0
, k Z.
2x
x
x
Ответ:
4
k
2
, k Z;
x
6
n, n Z ;
6
3
2 n, n Z
n, n Z
x
6
m, m Z
22. Метод введения вспомогательного угла
a cos x b sin x ca 2 b 2 A >0
а
а b
2
2
cos x
a
2
2
a b
2
b
a b
2
2
b
2
2
a b
sin x
c
a b
2
;
2
1
a
b
;
2
2
a2 b2
a b
sin cos x cos sin x 1,
sin( x) 1
x
x
2
n, n Z
sin
n, n Z
cos
2
a
a2 b2
b
a2 b2
23. Метод введения вспомогательного угла
sin x3 cos x 1: 2
1
sin x
2
cos
cos
3
3
1
cos x
2
2
1
3
, sin
2
3
2
3
sin x sin cos x
3
3
2
sin( ) sin cos cos sin
1
sin( x )
3
2
x
x
3
3
( 1) n arcsin
( 1) n
x ( 1) n
6
6
3
1
n, n Z
2
n, n Z
n, n Z
Ответ : x ( 1) n
6
3
n, n Z
24.
Правила.Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму – делай произведение.
25.
Проблемы, возникающие прирешении тригонометрических
уравнений.
26.
1.Потеря корней:делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
27. Можно ли насладиться решением уравнения sinx+cosx=1? Да, если стать его исследователем!
28. 1 способ: Введение вспомогательного аргумента
sin x cos x 1sin x cos x
2 sin( x ) 1
2
2
4
2 sin( x ) 1
sin
sin( x )
x
2
2
2 n, n z
4
3
x
2 n, n z
4
x 2 n, n z
x
2
2 n, n z
Ответ : 2 n, n z 2 n, n z
2
29. 2 способ: Применение универсальной подстановки
xx
sin x
2tg 2
1 tg 2 2x
1 tg 2 2
cos x
1 tg 2 2x
tg 2x y
2y
1 y2
1
1 y2 1 y2
2 y 1 y2
1
1 y2
2 y 1 y2 1 y2
y 0
2 y 2 y2 0
tg x 0
2
x
n, n z
2
y ( y 1) 0
x 2 n, n z
или
y 1
1 tg x 0
2
tg x 1
2
x
k , k z
2 4
x
Проверка. x 2 m, m
Ответ : 2 n, n z 2 k , k z
2
2
2 k , k z
30.
«Мне приходится делить времямежду политикой и уравнениями.
Однако уравнения, по-моему,
гораздо важнее.
Политика существует только для
данного момента, а уравнения
будут существовать вечно.»
А. Эйнштейн


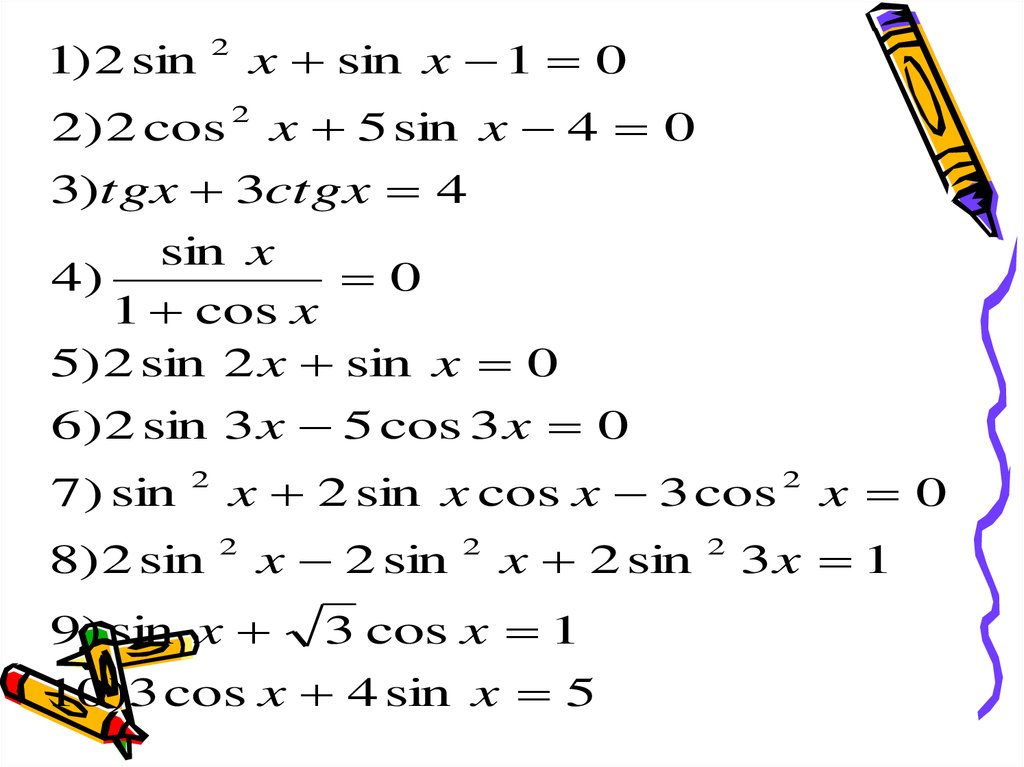








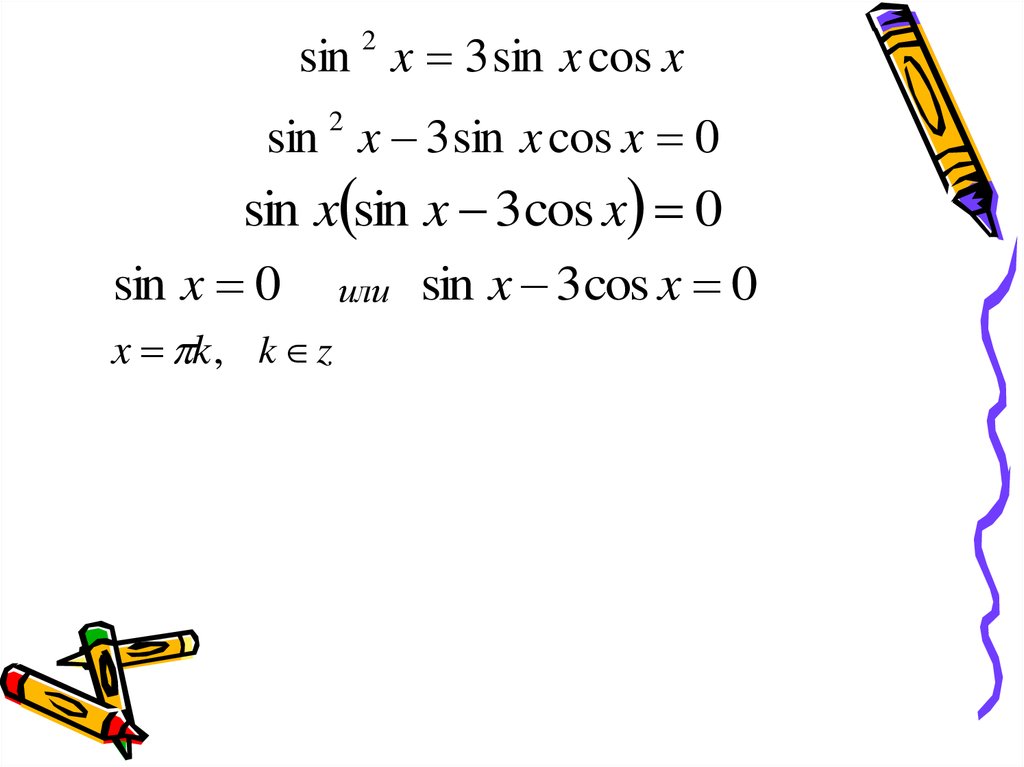
















 mathematics
mathematics








