Анаграммы. Квадратные уравнения

1. Анаграммы

Наритимскидн
Винаренуе
Фэкоцинетиф
Ерокнь

2.

Дискриминант
Уравнение
Коэффициент
Корень

3. Квадратные уравнения

4. (2m-5)х²+(4m+8)+36=0

При каких значениях параметра m
данное уравнение
А) является приведенным
квадратным уравнением
В) является неполным квадратным
уравнением
С) не является квадратным
уравнением

5.

А)
В)
С)
m=3
m = -2
m = 2,5

6.

18х²+х+2014=0

7. В каком древнем городе еще около 2ооо лет до н.э. первыми научились решать квадратные уравнения?

1.
2.
3.
4.
5.
6.
7.
Как называется уравнение вида ах2 +вх+с=0?
Название выражения в 2- 4 а с
Сколько корней имеет квадратное уравнение, если D > 0 ?
Сколько коней имеет квадратное уравнение если D=0 ?
Чему равен корень уравнения ах 2 = 0 ?
Как называется квадратное уравнение, где коэффициенты в
или с равны нулю?
Как называется квадратное уравнение, в котором первый
коэффициент
а =1

8.

Вавилон

9. Тест№1. Установите связь между квадратным уравнением и способами его решения

ах²+вх=0
ах²+вх+с=0
ах²+с=0
ах²=0
Уравнение не имеет
решений при х = с/ <0
а
Х=±√-с/а; -с/а>0
Х=0
Х= -в±√в²-4ас/2а
Х=0, х = -в/а

10. Тест№1. Проверьте правильность выполнения

Х=0, х = -в/а
Х= -в±√в²-4ас/2а
Уравнение не имеет решений при х =
Х=±√-с/а; -с/а>0
Х=0
-с/
а<0

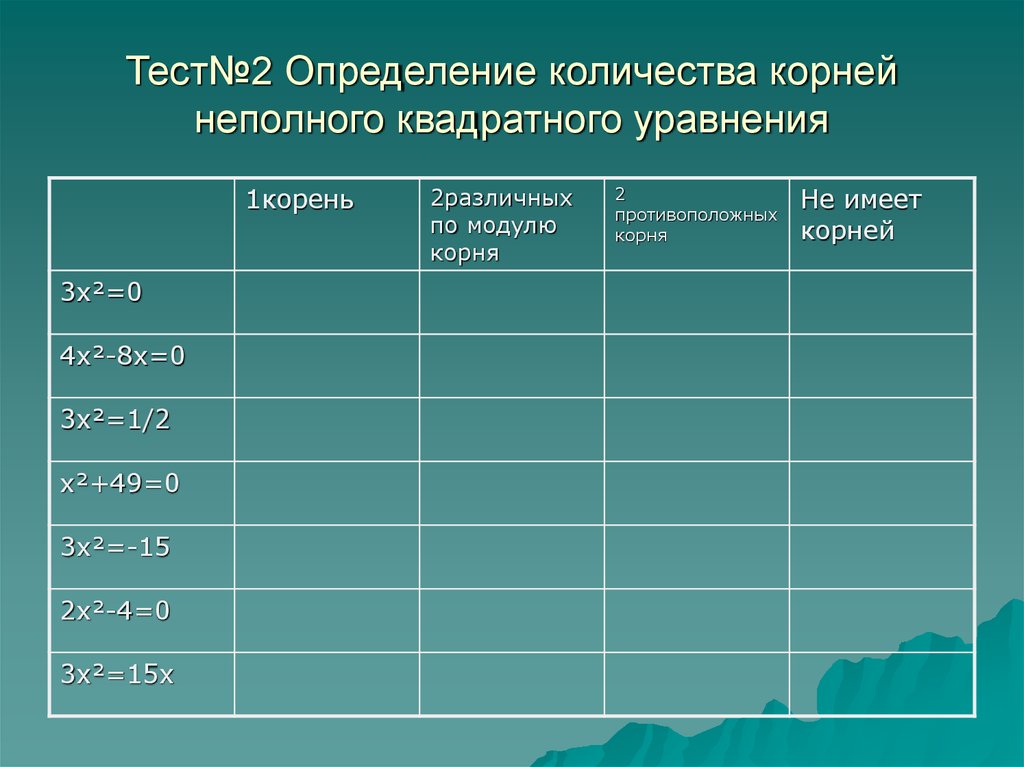
11. Тест№2 Определение количества корней неполного квадратного уравнения

1корень
3х²=0
4х²-8х=0
3х²=1/2
х²+49=0
3х²=-15
2х²-4=0
3х²=15х
2различных
по модулю
корня
2
противоположных
корня
Не имеет
корней

12. Тест№2 Проверьте правильность выполнения

1корень
3х²=0
4х²-8х=0
2различных
по модулю
корня
2
противоположных
корня
Не имеет
корней
+
+
+
3х²=1/2
х²+49=0
+
3х²=-15
+
+
2х²-4=0
3х²=15х
+

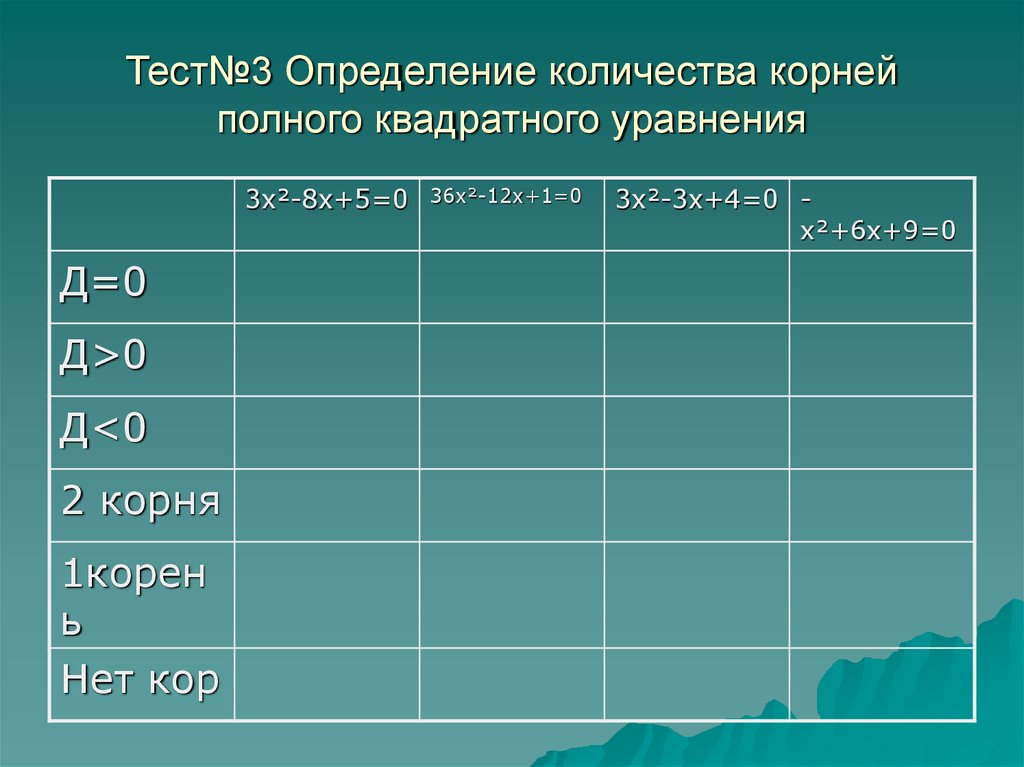
13. Тест№3 Определение количества корней полного квадратного уравнения

3х²-8х+5=0
Д=0
Д>0
Д<0
2 корня
1корен
ь
Нет кор
36х²-12х+1=0
3х²-3х+4=0 х²+6х+9=0

14. Тест№3 Проверьте правильность выполнения

3х²-8х+5=0
Д=0
Д>0
36х²-12х+1=0
+
+
+
Д<0
2корня
1корен
ь
Нет кор
3х²-3х+4=0 х²+6х+9=0
+
+
+
+
+

15. Найди «лишнее»

3х²+5х-8=0
0,3х²-х+7=0
х²-25=0
(х-2)(х+3)=0
4х²-5х+2-0
-х²+5х-8=0
3,5х²+х+1=0
х²+2х+8=0
х²-3х+4=0
3х²+5х-8=0
х²+х-8=0
7х+х²-8=0
3х²-х=0
х²-10х+25=0
х²-81=0
2х²=0

16. «Лишнее»

х²-25=0
х²+2х+8=0
3х²+5х-8=0
х²-10х+25=0

17. Задача Бхаскара

Обезьянок резвых стая
Всласть поевши, развлекаясь.
Их в квадрате часть восьмая
На поляне забавлялась.
А 12 по лианам…
Стали прыгать, повисая.
Сколько было обезьянок,
Ты скажи мне, в этой стае?

18. Решение Бхаскары

х²/
64+12=х
х²-64х=768
х²-64х+32²=-768+1024
(Х-32)²=256
Х-32=16
х-32=-16
Х=48
х=16
Ответ: 48 или 16 обезьянок

19. Практическая часть

1 вариант
2 вариант
А: х²-16х+15=0
А: х²-14х-15=0
В: -9=3х(2-х)
В: 10х=5(х²-3)
С:
С:
х²-5х
/
2
-3=0
х²-7х
/8 -1=0