Признак существования определенного интеграла. Лекция 2

1. Здравствуйте!

Лекция №7

2.

Признак существования определенного интеграла
Теорема. Для существования определенного интеграла
необходимо и достаточно, чтобы lim S s 0 .
0
Доказательство.
Необходимость. Пусть существует lim I . Это значит, что
0
0 I I .
Но тогда, учитывая, что s inf и S sup , можем записать
I s S I ,
откуда следует, что
S s ( I ) ( I ) 2 ,
и, в силу произвольности , это и означает, что lim S s 0 .
0

3.

Достаточность. Пусть lim S s 0 . Это означает, что
0
0 S s .
Но s I* I * S , откуда следует, что I * I* . Так как сколь
угодно мало, то это означает, что I * I* I .
Далее имеем s I S , s S ; следовательно, | I | , и, в
силу произвольности , это означает, что существует lim I .
0

4.

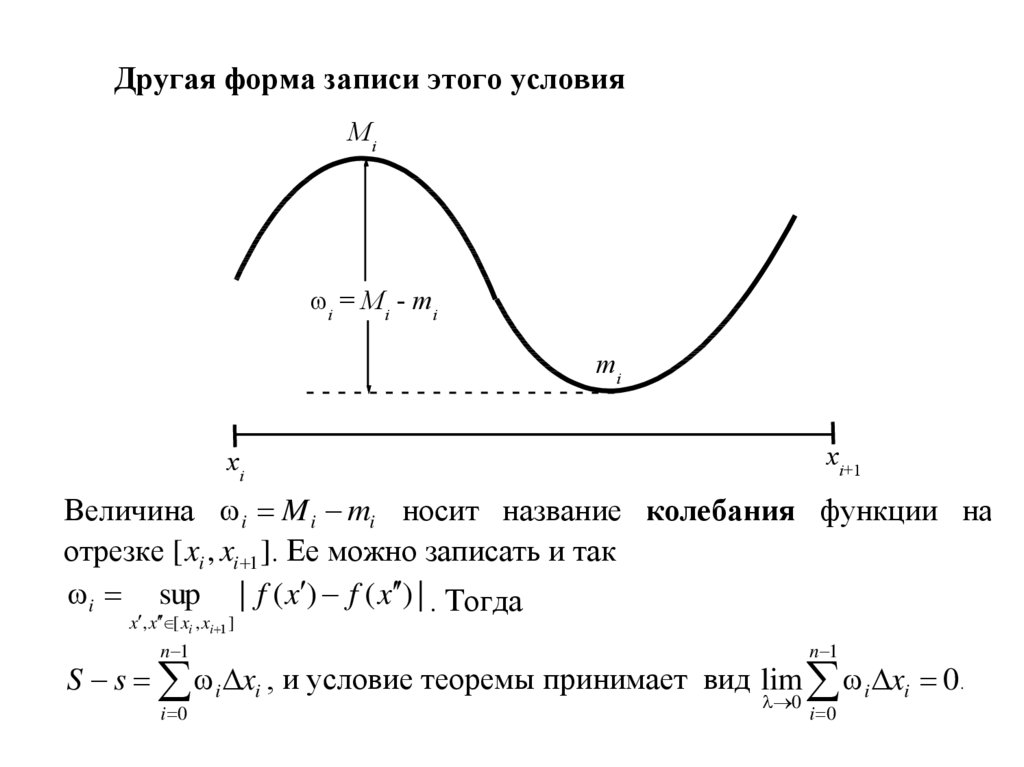
Другая форма записи этого условия
Mi
i = Mi - mi
mi
xi+1
xi
Величина i M i mi носит название колебания функции на
отрезке [ xi , xi 1 ]. Ее можно записать и так
i sup | f ( x ) f ( x ) | . Тогда
x , x [ xi , xi 1 ]
n 1
n 1
S s i xi , и условие теоремы принимает вид lim i xi 0 .
i 0
0
i 0

5.

Классы интегрируемых функций
Теорема 1. Если функция f (x) непрерывна на отрезке [a, b] ,
то она интегрируема на этом отрезке.
Доказательство.
Если функция f (x) непрерывна на отрезке [a, b] , то она, по
теореме Кантора, равномерно непрерывна на этом отрезке. В
обозначениях этой главы, это означает, что
0 0 xi i .
Возьмем любое . Тогда i i и мы получаем
n 1
n 1
i 0
i 0
0 i xi xi (b a)
n 1
и, в силу произвольности , отсюда следует, что lim i xi 0 .
0
i 0

6.

Теорема 2. Если функция f (x) ограничена на отрезке [a, b] и
имеет на нем лишь конечное число точек разрыва, то она
интегрируема на этом отрезке.
Доказывать эту теорему мы не будем.

7.

Теорема 3. Если функция f (x) монотонна и ограничена на
отрезке [a, b], то она интегрируема на этом отрезке.
Доказательство.
Пусть, для определенности, функция f (x) монотонно
возрастает. Возьмем произвольное и положим
.
f (b) f (a)
Разобьем весь отрезок [a, b] на кусочки, длина каждого из которых
xi будет меньше . Тогда на кусочке [ xi , xi 1 ] будет
i f ( xi 1 ) f ( xi ) и мы получим
n 1
n 1
n 1
i 0
i 0
i 0
0 i xi i f ( xi 1 ) f ( xi )
( f ( x1 ) f ( x0 )) ( f ( x2 ) f ( x1 )) ( f ( x3 ) f ( x2 )) ... ( f ( xn ) f ( xn 1 ))
f ( xn ) f ( x0 ) f (b) f (a) ,
n 1
и, в силу произвольности , отсюда следует, что lim i xi 0.
0
i 0

8.

Свойства интегрируемых функций
1. Если функция f (x) интегрируема на [a, b] , то функция kf (x)
также интегрируема на [a, b] .
Пусть i sup | f ( x ) f ( x ) | есть колебание функции f (x)
x , x [ xi , xi 1 ]
на отрезке [ xi , xi 1 ]. Тогда ее интегрируемость на отрезке [a, b]
означает, что
n 1
x 0 .
i 0
i
0
i
Пусть далее i есть колебание функции kf (x) на отрезке [ xi , xi 1 ].
Тогда имеем
i sup | kf ( x ) kf ( x ) | | k | sup | f ( x ) f ( x ) | | k | i ,
x , x [ xi , xi 1 ]
и поэтому
x , x [ xi , xi 1 ]
n 1
x
i 0
i
i
n 1
| k | i xi
0 ,
0
i 0
откуда и следует интегрируемость функции kf (x) на [a, b] .

9.

2. Если функция f (x) интегрируема на [a, b] , то функция | f ( x) |
также интегрируема на [a, b] .
Пусть i есть колебание функции | f ( x) | на отрезке [ xi , xi 1 ].
Тогда имеем
i sup | f ( x ) | | f ( x ) | sup | f ( x ) f ( x ) | i
x , x [ xi , xi 1 ]
x , x [ xi , xi 1 ]
(воспользовались неравенством | a b | | a | | b | , написанным в
обратном порядке) и поэтому
n 1
n 1
i 0
i 0
0 i xi i xi
0 ,
0
откуда и следует интегрируемость функции | f ( x) | на [a, b] .

10.

3. Если функции f (x) и g (x ) интегрируемы на [a, b] , то функция
f ( x) g ( x) также интегрируема на [a, b] .
Пусть i sup | f ( x ) f ( x ) | и i sup | g ( x ) g ( x ) |
x , x [ xi , xi 1 ]
x , x [ xi , xi 1 ]
есть колебания функций f (x) и g (x ) на
отрезке [ xi , xi 1 ]
соответственно. Тогда для колебания их суммы или разности имеем
i sup | ( f ( x ) g ( x )) ( f ( x ) g ( x )) |
x , x [ xi , xi 1 ]
sup {| f ( x ) f ( x ) | | g ( x ) g ( x ) |}
x , x [ xi , xi 1 ]
(модуль суммы или разности не превосходит суммы модулей)
sup {| f ( x ) f ( x ) |} sup {| g ( x ) g ( x ) |} i i
x , x [ xi , xi 1 ]
x , x [ xi , xi 1 ]
(супремум суммы не превосходит суммы супремумов). Поэтому
n 1
n 1
n 1
i 0
i 0
i 0
0 i xi i xi i xi
0
0
откуда и следует интегрируемость функции f ( x) g ( x) на [a, b] .

11.

4. Если функции f (x) и g (x ) интегрируемы на [a, b] , то функция
f ( x) g ( x) также интегрируема на [a, b] .
Вспомним, что пока мы умеем интегрировать только
ограниченные функции. Это значит, что sup | f ( x) | M f и
x [ a , b ]
sup | g ( x) | M g . Тогда имеем
x [ a , b ]
f ( x ) g ( x ) f ( x ) g ( x ) [ f ( x ) f ( x )]g ( x ) [ g ( x ) g ( x )] f ( x ) ,
| f ( x ) g ( x ) f ( x ) g ( x ) | | f ( x ) f ( x ) | M g | g ( x ) g ( x ) | M f ,
и для колебания i функции f ( x) g ( x) на отрезке [ xi , xi 1 ] имеем
i M g i M f i
и поэтому
n 1
n 1
n 1
i 0
i 0
i 0
0 i xi M g i xi M f i xi
0 ,
0
откуда и следует интегрируемость функции f ( x) g ( x) на [a, b] .

12.

5. Если функция f (x) интегрируема на [a, b] , то она
интегрируема на любой части этого промежутка.
Пусть отрезок [c, d ] [a, b] разобьем отрезок [a, b] на кусочки,
так, чтобы точки с и d оказались в числе точек деления (см. рис.).
d
c
a
Тогда имеем
0
x
i:xi [ c , d )
i
i
b
x 0 ,
i:xi [ a , b )
i
i
0
что и доказывает интегрируемость f (x) на отрезке [c, d ].

13.

6. Если отрезок [a, b] разбит на части и функция f (x)
интегрируема на каждой из частей, то она интегрируема и на [a, b] .
Пусть отрезок [a, b] разбит на две части точкой с (см. рис.).
b
c
a
Разобьем отрезок [a, b] на части так, чтобы точка с вошла в число
точек деления. Если функция f (x) интегрируема на отрезках [a, c] и
0 и i xi
0 .
[c, b], то это значит, что i xi
0
0
i:xi [ a , c )
Но тогда
x
i:xi [ a , b )
i
i
i:xi [ c , b )
x x 0 ,
i:xi [ a , c )
i
i
i:xi [ c , b )
i
i
0
что и доказывает интегрируемость f (x) на отрезке [a, b] .