Similar presentations:
Квантовая статистика
1.
Квантовая статистикаВ классической механике частицы одинаковой природы
можно различать, пронумеровав (пометив) можно следить
при движении по траектории и в любой момент указать на
нужную частицу.
В квантовой механике, в силу принципа неопределенности,
нет понятия траектории,
следить и различать невозможно
потеря индивидуальности
глубокие физические следствия.
2.
Квантовая статистикаРассмотрим систему из двух тождественных частиц.
Координаты одной 1, другой 2 Функция ψ( 1, 2),
не меняется при перестановке ,т.е. не меняются физические
свойства системы.
ψ( 1, 2) 2 = ψ( 2, 1) 2
Возможны два случая:
симметричная ψ – функция
ψ( 1, 2) = ψ( 2, 1),
и антисимметричная ψ – функция
ψ( 1, 2) = – ψ( 2, 1).
3.
Квантовая статистикаЧастицы с целым и нулевым спином могут находиться в
пределах одной системы в неограниченном количестве.
Подчиняются статистике Бозе – Эйнштейна, называются
бозонами, описываются симметричной функцией.
Частицы с полуцелым спином (электроны, нуклоны)
описываются антисимметричными ψ – функциями,
находятся в квантовых состояниях поодиночке (принцип
Паули). Подчиняются статистике Ферми – Дирака и
называются фермионами.
4.
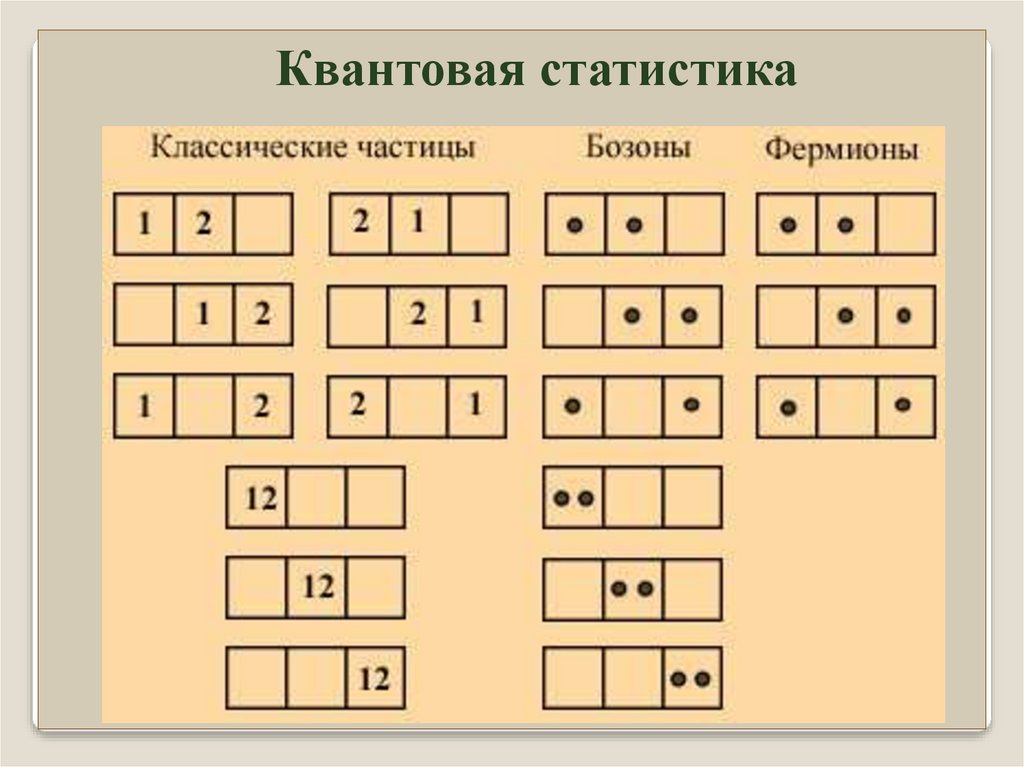
Квантовая статистикаФермионы и бозоны при размещении по ячейкам ведут себя
по-разному.
Фермионы согласно принципу Паули.
Для бозонов вероятность рождения в состоянии, где уже есть
n бозонов, пропорциональна n (бозоны любят накапливаться).
Идеальный ферми-газ и идеальный бозе-газ.
Количество частиц – N, количество фазовых ячеек Z, число
способов, которыми можно распределить N частиц по Z
ячейкам – Ω.
Ω – статистический вес системы.
Задача – его определить, найти Ω(N,Z).
Если N = Z, то фермионы распределяются только одним
способом: по одной частице в ячейку.
5.
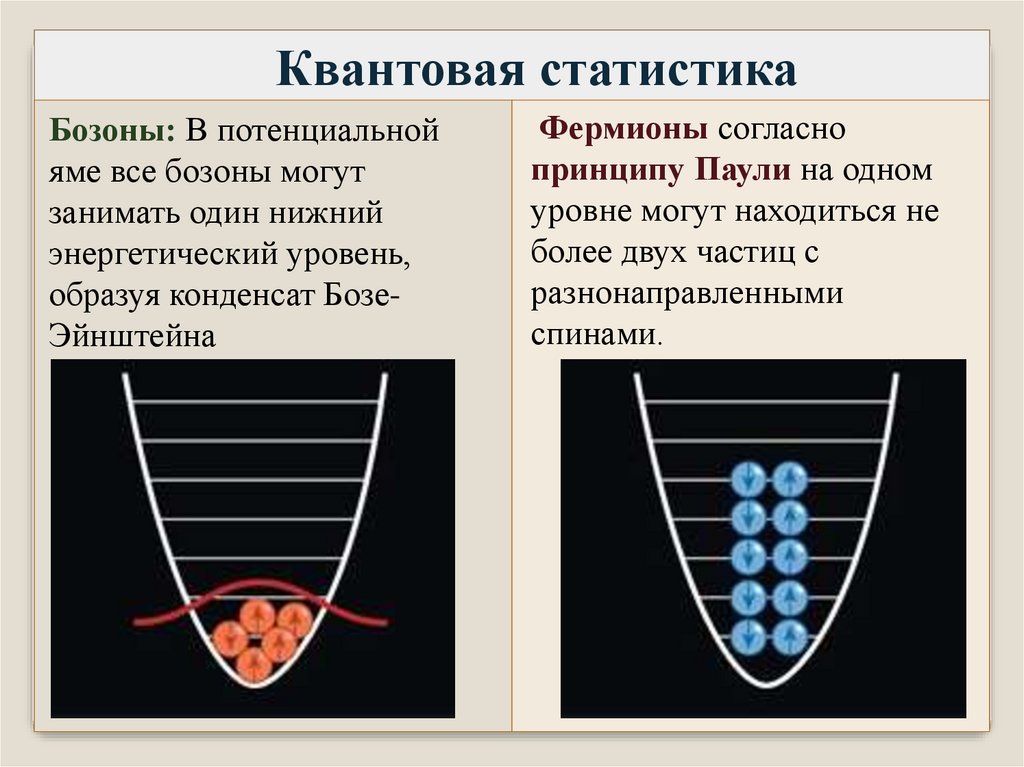
Квантовая статистикаБозоны: В потенциальной
яме все бозоны могут
занимать один нижний
энергетический уровень,
образуя конденсат БозеЭйнштейна
Фермионы согласно
принципу Паули на одном
уровне могут находиться не
более двух частиц с
разнонаправленными
спинами.
6.
Фазовое пространствоОдной из основных задач статистической физики является
нахождение закона распределения частиц по разным
квантовым состояниям.
Рассматривается система невзаимодействующих частиц
(идеальный газ, невырожденный). Каждая частица может
находиться в состояниях с энергиями: <ε1>,
<ε2>, …
Равновесному состоянию системы соответствует среднее
число заполнений состояний с соответствующими энергиями:
<n1>, < n2>, … (дробные).
Задача заключается в нахождении наиболее вероятного
распределения частиц по ячейкам.
7.
Фазовое пространствоФазовое пространство – шестимерное пространство с
взаимно-перпендикулярными осями:
x, y, z, px, py, pz –,.
Состояние частицы с координатами xi, yi, zi, и импульсами
pxi, pyi, pzi –обозначается в этом пространстве точкой.
Но из принципа неопределенности:
x px∙ y py∙ z pz = ħ3
возможно только определить ячейку, объемом ħ3 в фазовом
пространстве, в которую попадает частица.
8.
Квантовая статистика9.
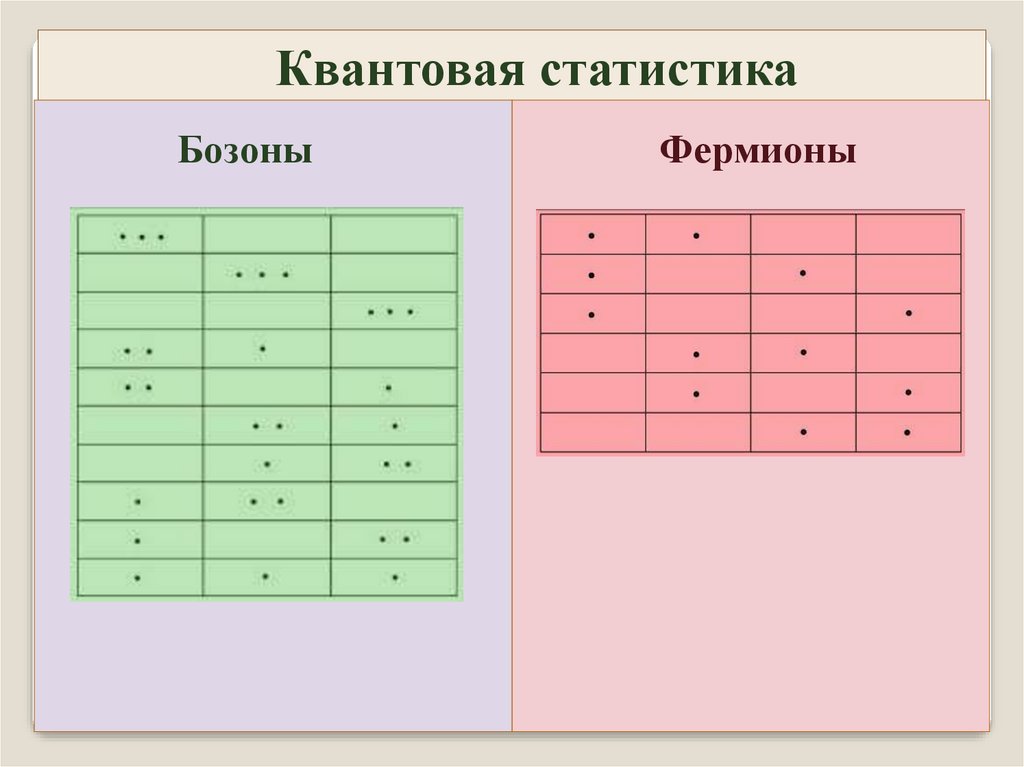
Квантовая статистикаБозоны
Фермионы
10.
Квантовая статистикаДля бозонов считаем все
возможные перестановки
частиц и перегородок
(N + Z – 1)!, ничего не
меняют перестановки между
собой частиц и между собой
перегородок
Z N 1 !
B
Z 1 ! N!
Для фермионов считаем
все возможные
перестановки ячеек
(пустых и занятых) Z!,
перестановки местами
частиц N! и пустых ячеек
(Z – N)! ничего не меняют.
Z!
F
Z N ! N!
11.
Квантовая статистикаЭнергия частицы ε зависит от координат и импульса
ε = f(x, y, z, px, py, pz).
По аналогии с уравнением поверхности в трехмерном
пространстве: f(x, y, z) = const ,Гиперповерхность в
фазовом пространстве, все точки которой соответствуют
одной и той же энергии частицы.
Между двумя близкими поверхностями
f(x, y, z, px, py, pz) = εi и f(x, y, z, px, py, pz) = εi + εi
образуется тонкий энергетический слой. Все пространство
разбивается на такие слои. В пределы тонкого слоя попадает
Zi ячеек и Ni частиц.
Z i N i 1 !
Bi
Zi 1 ! Ni !
Zi!
Fi
Zi Ni ! Ni !
12.
Квантовая статистикаСтатистический вес системы равен произведению
Zi Ni 1 !
B Bi
Zi 1 ! Ni !
Zi !
F
Z i Ni ! Ni !
Надо найти наиболее вероятное распределение частиц по
ячейкам, т.е. найти максимум этого выражения при условиях:
N i = N и εiN i =E.
То же самое: искать максимум энтропии: S = klnΩ.
S B k ln Ni Zi 1 ! ln Ni ! ln Zi 1 !
S F k ln Zi ! ln Ni ! ln Zi Ni !
13.
Квантовая статистикаПосле сложных математических преобразований (формула
Стирлинга, множители Лагранжа) получаются формулы:
Для фермионов:
Для бозонов:
Ni Z i 1
i
exp
Ni
k
1
T
Z i Ni
i
exp
Ni
k
T
14.
Квантовая статистикаРаспределение
Ферми- Дирака
Распределение
Бозе – Эйнштейна.
ni
B
1
i
exp
1
kT
ni
F
1
i
exp
1
kT
Отличаются только знаком в знаменателе.
15.
Квантовая статистикаПри малых по сравнению
с единицей числах
заполнения, единицей в
знаменателе можно
пренебречь, оба
распределения переходят в
распределение Больцмана.
16.
Квантовая статистикаПараметр распределения μ называется химическим
потенциалом. Является функцией температуры,
определяется, как и энергия частицы, с точностью до
аддитивной постоянной.
Для фермионов при абсолютном нуле μ может быть только
положительной величиной (иначе <ni> = 0).
Химический потенциал для бозонов, наоборот, не может
быть положительным (некоторые заполнения будут
отрицательными). Более того, если число частиц переменное
и Ni ≠ N μ = 0
для бозе-газа с переменным числом частиц
ni
B
1
i
exp 1
kT
17.
Квантовая статистика18.
Фотонный газ и формула ПланкаПри обычных (не лазерных) интенсивностях световые волны
не возмущают друг друга. равновесное излучение в полости
можно представить как идеальный фотонный газ.
Энергия фотона
εi= ħ i
Число фотонов не является заданной константой, т.к. стенки
полости поглощают и испускают фотоны. распределение
их описывается формулой:
1
ni
i
exp
1
kT
19.
Фотонный газ и формула ПланкаЭнергия фотона не зависит от координат и от направления
движения, изоэнергетическая поверхность представляет
сферу в пространстве импульсов. объем тонкого
энергетического слоя:
Py
Vμ = V∙4πp2dp
Число ячеек Zi в этом слое
определяется как
Px
2∙ Vμ / h3,
P
т.к. в каждой ячейке два
состояния фотона
с разной поляризацией.
dP
Pz
8 p dp
p dp
Zi
V V
;
8
2
i
3 3
2
i
2 3
20.
Фотонный газ и формула ПланкаУчитывая
i
pi
;
c
d
Zi V
;
c
2
i
2 3
и
d i
;
dpi
c
Ei = Zi·<ni>·ħ i
d
Ei V
c
3
i
2 3
Совпадает с формулой Планка.
d
u , T
c
3
i
2 3
e
1
e
1
kT
kT
1
;
1
;
21.
Фононный газ и формула ДебаяАналогично, колебания
кристаллической решетки
можно представить как
фононный газ.
22.
Фононный газ и формула ДебаяХотя фононы – квазичастицы, они подчиняются той же
статистике и к ним применяется распределение Бозе –
Эйнштейна
2
3 i d
Zi V
;
2 3
2 c
3 d
Ei V
2 c
3
i
2 3
1
e
kT
(Три вида поляризации)
;
1
3
E E0 V
2 2c 3
v 6 n;
3
m
3
2
m
0
i3d
e
Формула Дебая.
kT
;
1
23.
Фононный газ и формула ДебаяПлотность энергии
Для упругих волн в
кристалле:
u dN
9n 1
2
u 3
d
m 0 2
e kT 1
m
3
u0
2 2v 3
3 kT
u0 2 3
2 v
m
3
0
4 m
e
kT
3
d
1
x dx
4
0 e x 1 u0 BT
24.
Распределение Ферми-Диракаni
F
1
f
i
exp
1
kT
f(ε)
1
.5
0
T=0
T>0
εF
ε
25.
Электронный газ в металлах26.
Электронный газ в металлахВалентные электроны в металлах свободно перемещаются в
пределах образца и обуславливают его проводимость,
электроны проводимости. Они ведут себя подобно молекулам
идеального газа, электронный газ = идеальный ферми –
газ.
27.
Электронный газ в металлахМеталлический образец представляет собой для электронов
трехмерную потенциальную яму, квантование энергии.
Электроны распределяются по
энергетическим уровням в
соответствии с функцией
Ферми – Дирака. Электроны
0 A
обладают одной и той же
энергией в двух состояниях,
F
различающихся спином.
Среднее число на уровне с
энергией εi:
ε
ε
параметр μ обозначен εF
(энергия Ферми).
2
ni
i F
exp
kT
1
28.
Электронный газ в металлахПри абсолютном нуле электроны
располагаются попарно на самых
низких уровнях:
<ni> = 2 если εi εF
εF
<ni> = 0 если εi εF
при T
ε
T=0
f(ε)
0
1
= 0 εF = εmax,
f(ε)
1
T=0
0.5
0
εF
ε
29.
Теплоемкость электронного газаε
T>0
При температурах T ≠ 0
отличие наблюдается лишь в
области порядка kT.
f(ε)
εF
f(ε)
1
при
0
εi= εF ; <ni> = ½
1
½
0
T>0
εF
независимо от T.
Определение: Уровень Ферми – это энергия, при которой
функция распределения Ферми – Дирака
f = ½.
ε
30.
Электронный газ в металлах31.
Электронный газ в металлах2
2
Для свободных электронов U = 0
;
2m
r c exp ikr ;
P
y
2
2
2
p
k
p
k ;
;
2m 2m
В случае свободных электронов
изоэнергетическая поверхность εi= εF
в k – пространстве имеет форму сферы:
поверхность
Ферми
2
2
k
F;
2m
P=ћk
Pz
Px
При T = 0 отделяет состояния,
заполненные электронами, от
незаполненных.
32.
Электронный газ в металлахТ.к. каждой ячейке соответствуют два состояния с разными
спинами, число состояний
V i
1
p dp
m 2m i 2 i
2
Zi 2 3 V
V
A
i i ;
2 3
h
2
i
2 3
3
где
V 2m 2
A
;
2
2
2
1
33.
Электронный газ в металлахпри T = 0 заполнены N нижних состояний N = nV,
где n – концентрация свободных электронов,
N = Zi
F
2 32
т.к. εi εi N A d A F ;
3
0
1
2
2
2
F 0
3 n 3 ;
2m
2
Для концентрации n = 5∙1028м–3
температура Ферми TF = 6∙104 К
TF
F 0
k
εF = 5 эВ.
34.
Электронный газ в металлахСредняя энергия электронов при абсолютном нуле:
E Zi i A i 2 i ;
3
F
2 52
2
E A d A F ;
5
0
3
3
F 0
5
= 3 эВ, соответствует 2.5∙104 К
Уровень ферми слабо зависит от температуры, при kT εF
2 kT 2
F 0 ;
F F 0 1
12 F 0
35.
Электронный газ в металлах36.
Электронный газ в металлахВырожденным
называется идеальный
газ, распределение
частиц которого по
энергиям сильно
отличается от
классического.
T TF вырожденный,
T TF не
вырожденный.
37.
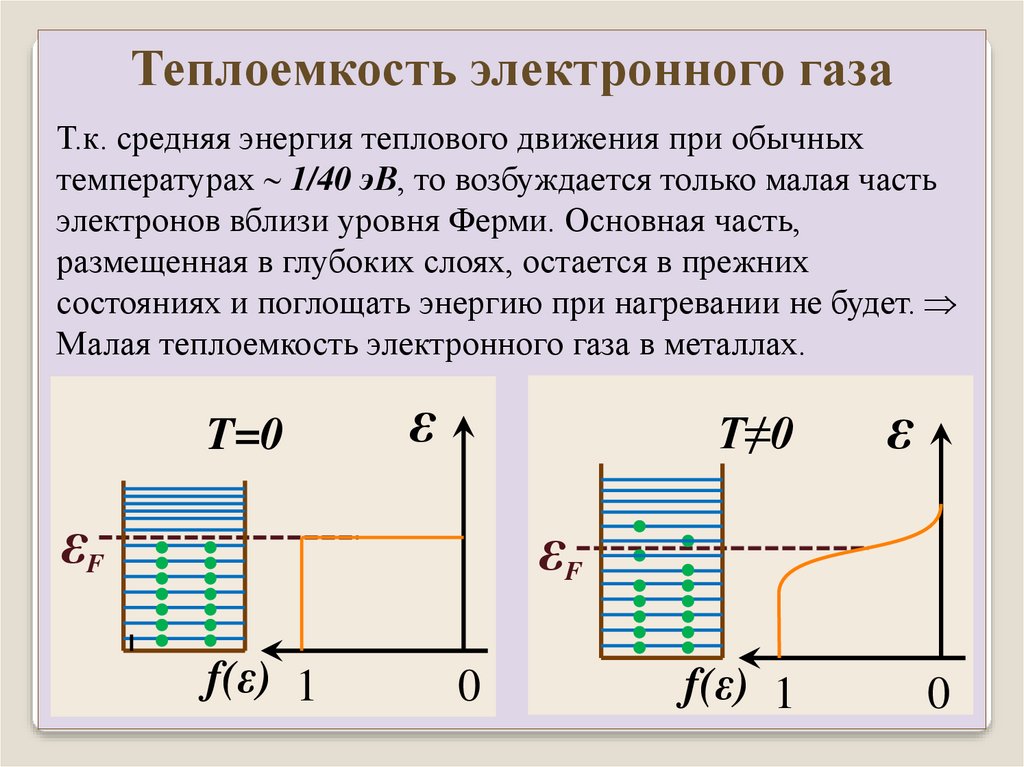
Теплоемкость электронного газаТ.к. средняя энергия теплового движения при обычных
температурах 1/40 эВ, то возбуждается только малая часть
электронов вблизи уровня Ферми. Основная часть,
размещенная в глубоких слоях, остается в прежних
состояниях и поглощать энергию при нагревании не будет.
Малая теплоемкость электронного газа в металлах.
T=0
ε
T≠0
εF
ε
εF
f(ε) 1
0
f(ε) 1
0
38.
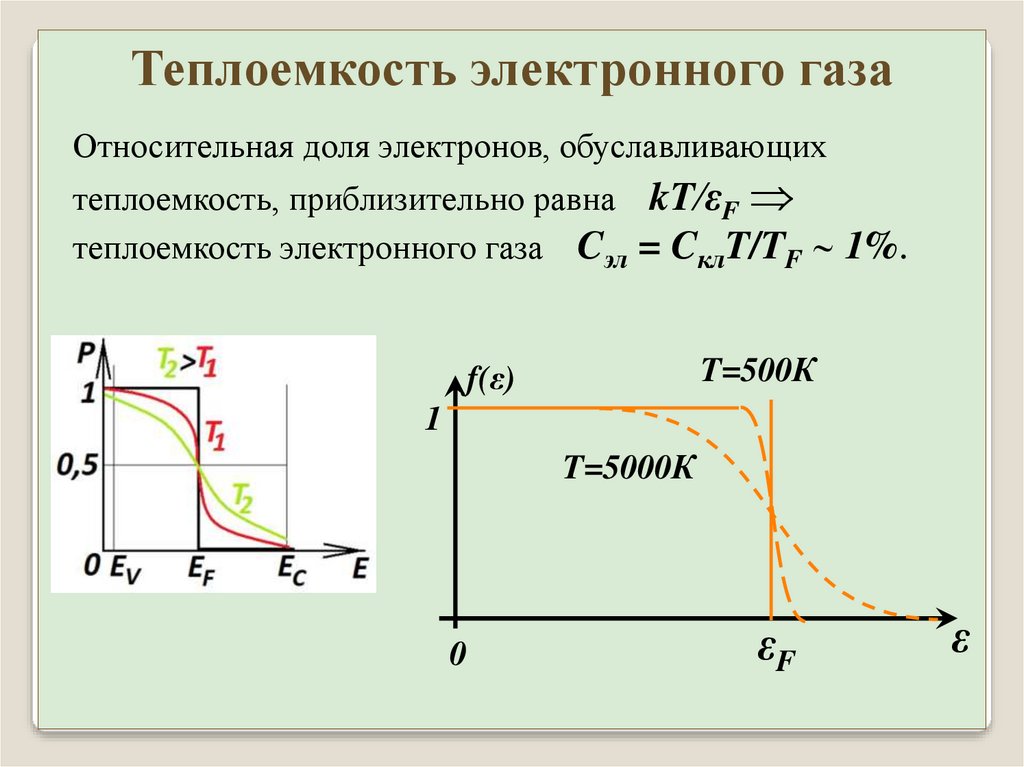
Теплоемкость электронного газаОтносительная доля электронов, обуславливающих
теплоемкость, приблизительно равна kT/εF
теплоемкость электронного газа Cэл = CклT/TF 1%.
T=500К
f(ε)
1
T=5000К
0
εF
ε



































 physics
physics








