Similar presentations:
Элементы квантовой статистики
1.
ЭЛЕМЕНТЫ КВАНТОВОЙСТАТИСТИКИ
2.
Квантовая статистика –разделфизики, исследующий поведение
многих частиц, подчиняющихся
квантовым законам.
3.
ПРИНЦИП НЕРАЗЛИЧИМОСТИТОЖДЕСТВЕННЫХ ЧАСТИЦ
Будем рассматривать
многоэлектронные системы
Если частицы имеют одинаковые
физические характеристики ( масса,
заряд, спин, квантовые числа) , то
они наз. ТОЖДЕСТВЕННЫМИ
4.
В классической механике можновсегда отследить поведение частицы
– ее траектория известна
5.
В квантовой механике понятиятраектории нет
Можно говорить только о
вероятности обнаружения частицы в
данной точке пространства
6.
Если волновые функции двух частицперекрываются, то решить вопрос,
какая из двух частиц находится в
данной области – невозможно.
В квантовой механике частицы
теряют свою индивидуальность и
становятся неразличимыми.
7.
ПРИНЦИП неразличимоститождественных частиц
Невозможно экспериментально
различить тождественные частицы
8.
xiЕсли обозначить
волновую функцию
системы 2
электронов
( x1 , x2 )
Совокупность пространственных и спиновых
координат i частицы
( x2 , x1 )
Частицы поменялись местами
9.
Из принципа неразличимости( x1 , x2 ) ( x2 , x1 )
2
2
( x1, x2 ) ( x2 , x1 )
Симметричная волновая функция
( x1, x2 ) ( x2 , x1 )
Антисимметричная волновая функция
10.
Симметрия или антисимметрияопределяется спином частиц
Частицы с полуцелым спином
(электроны, протоны, нейтроны)
описываются антисимметричными
волновыми функциями и наз.
ФЕРМИОНАМИ
Частицы с нулевым или целым
спином( мезоны, фотоны)
описываются симметричными
волновыми функциями и наз.
БОЗОНАМИ
11.
Поведение фермионов описываетсястатистикой Ферми-Дирака
Поведение бозонов - статистикой
Бозе -Эйнштейна
12.
Обобщенный принцип ПаулиСистемы фермионов встречаются в
природе только в состояниях,
описываемых антисимметричными
волновыми функциями.
Количество бозонов, находящихся в
одинаковом состоянии не
ограничивается
13.
РАСПРЕДЕЛЕНИЕФЕРМИ-ДИРАКА
Вероятность
обнаружения
электрона с
энергией Е при
температуре Т
EF
-
f (E)
1
1 e
E EF
kT
Уровень Ферми (химический потенциал)
-Уровень Ферми – максимальная энергия,
которую может иметь электрон при Т=0
k -постоянная Больцмана
14.
При Т=0E EF
e
E EF
kT
e
E EF
0
e
1
0
f (E)
1 0
15.
При Т=0E EF
e
E EF
0
e
1
1
f (E)
1 0
1 0
e
16.
f(Е)kT
1
Т=0
0.5
Т >0
ЕF
Е
kT
17.
f ( E EF )1
1 e
EF EF
kT
1
1
1
0
1 e
1 1
2
18.
1) Электроны заполняют нижниеуровни в соответствие с принципом
Паули
2) При Т=0 максимально возможная
энергия электрона – это энергия
Ферми
E E
3) при E E F , e
f (E) e
E
kT
F
kT
1
Распределение
Больцмана
19.
kT EFЭлектронный газ называется вырожденным
и подчиняется статистике Ферми-Дирака
kT EF
Электронный газ называется невырожденным
и подчиняется статистике Больцмана
20.
Статистика Бозе-Эйнштейна1
f B (E)
e
E EB
kT
1
EB – химический потенциал
системы бозонов
21.
ФИЗИКА ТВЕРДОГО ТЕЛА22.
Металлы,диэлектрики,полупроводники
В твердом теле при сближении
атомов отдельные уровни
расщепляются и объединяются в
зоны
23.
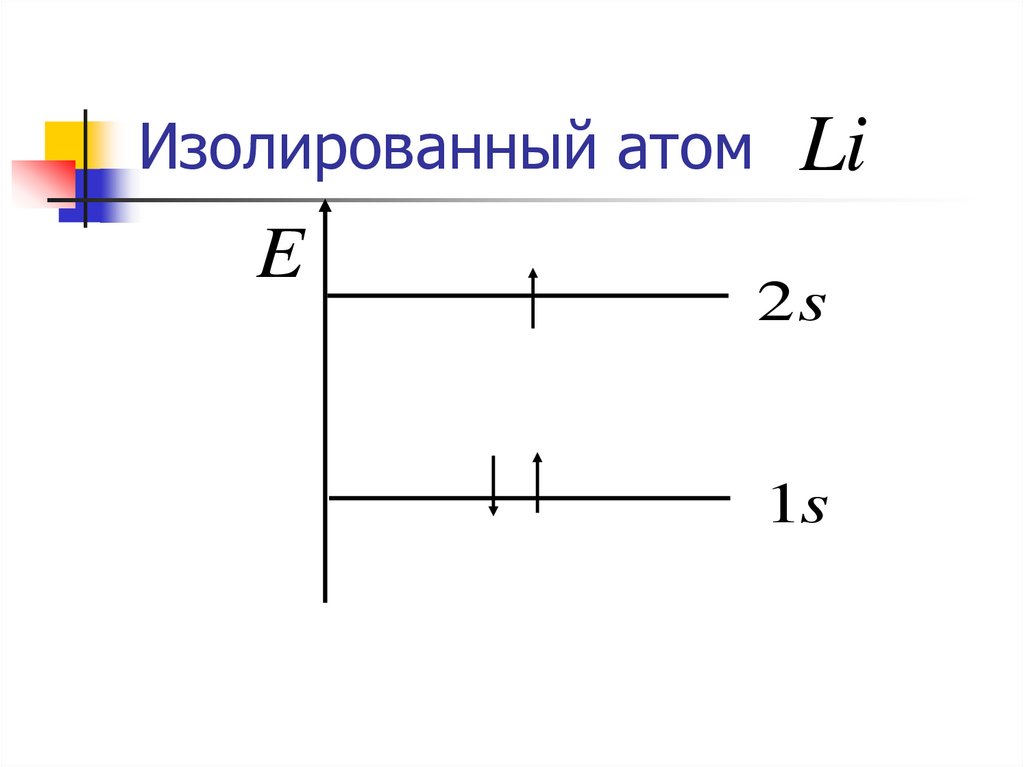
24.
Изолированный атомE
Li
2s
1s
25.
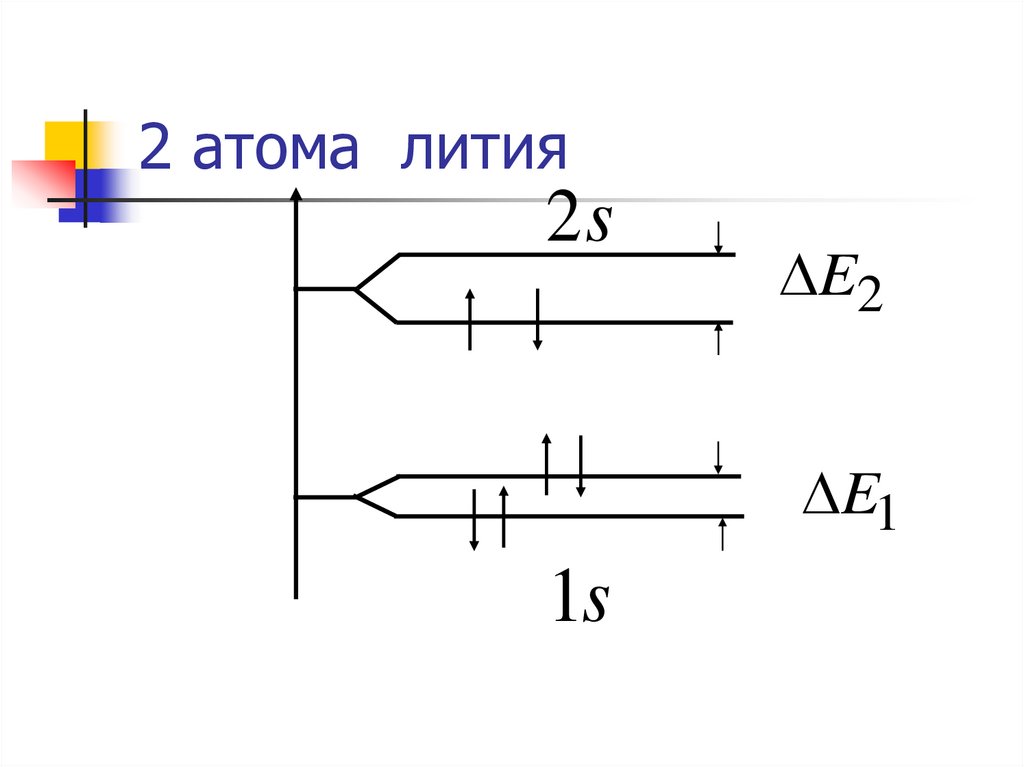
2 атома лития2s
E2
E1
1s
26.
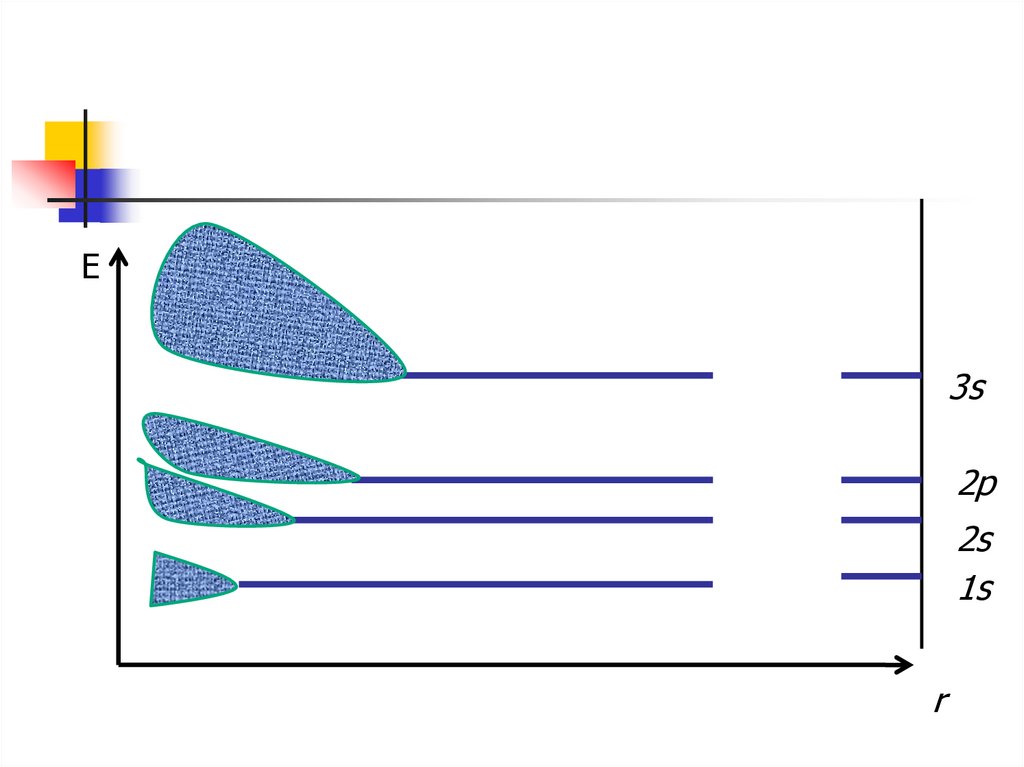
Е3s
2p
2s
1s
r
27.
Образуются разрешенные областиэнергии
В разрешенной зоне столько
дискретных уровней ,сколько их
содержится во всех изолированных
атомах
Разрешенные зоны разделены
промежутками энергии –
запрещенными зонами
28.
Металлы,диэлектрики,полуроводники
1) Существуют либо полностью
заполненные, либо полностью
свободные зоны
∆E
∆E-ширина запрещенной зоны
между последней полностью
заполненной и следующей
свободной зоной
29.
Если ∆E < 3 эВ , то такие веществаназываются полупроводниками
Электрону может хватить тепловой
энергии, чтобы перейти из одной зоны в
другую
Если ∆E >5 эВ то такие вещества
называются диэлектриками
30.
2) Верхняя зона заполнена частично3)Полностью заполненная зона
перекрывается со следующей свободной
31.
Такие вещества называютсяметаллами
32.
Собственные и примесныеполупроводники
Собственный полупровдник, когда в
нем отсутствуют примеси
Eс
зона проводимости
∆Е – запрещенная зона
Ev Валентная зона
33.
Примесный полупроводники – вкристаллической решетки
встречаются атомы посторонней
примеси
34.
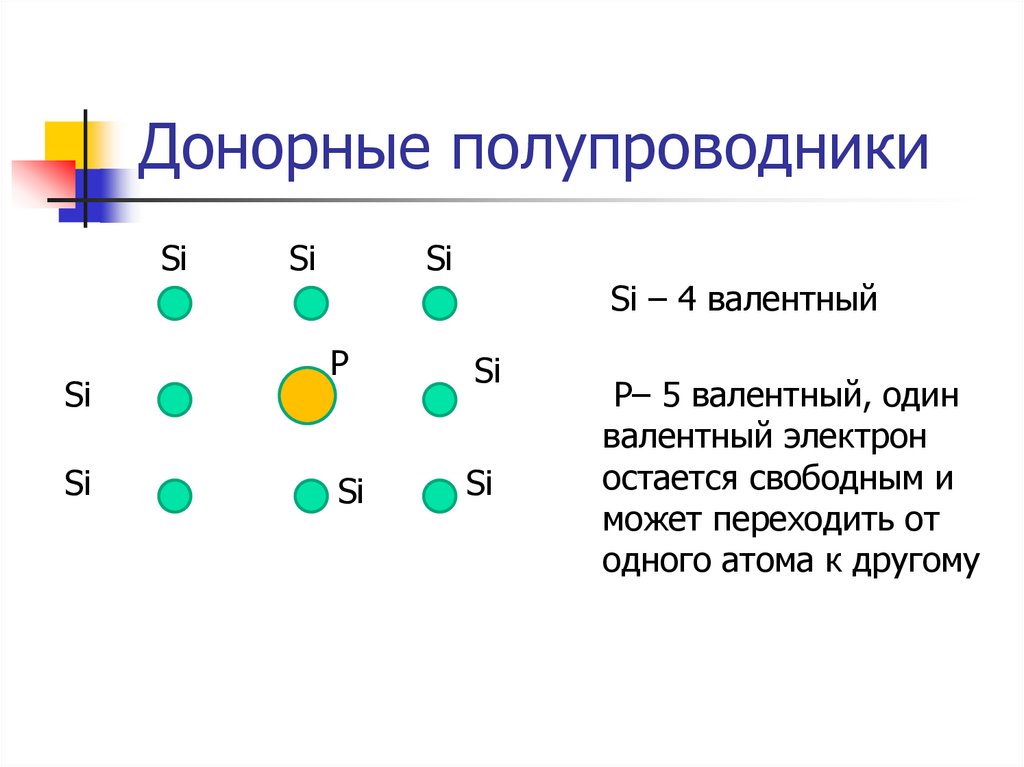
Донорные полупроводникиSi
Si
Si
Si
Si
Si – 4 валентный
P
Si
Si
Si
P– 5 валентный, один
валентный электрон
остается свободным и
может переходить от
одного атома к другому
35.
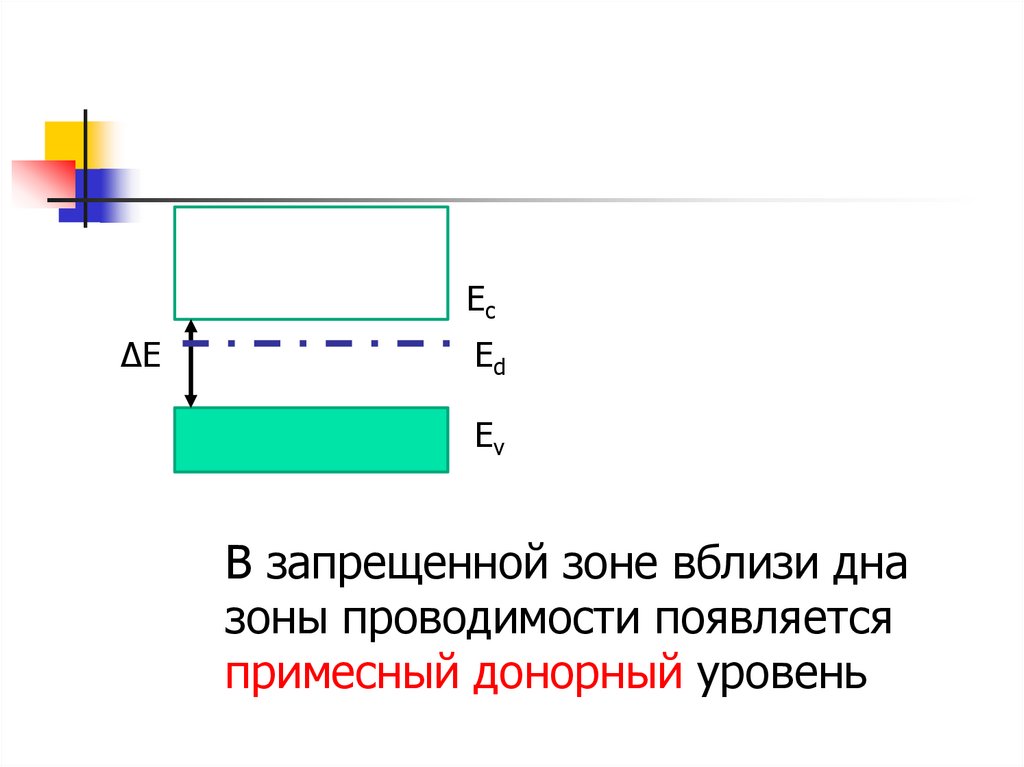
Eс∆Е
Ed
Ev
В запрещенной зоне вблизи дна
зоны проводимости появляется
примесный донорный уровень
36.
Акцепторныеполупроводники
Si
Si
Si
Si
Si
Si – 4 валентный
в
Si
Si
Si
В– 3 валентный, одна
валентная связь остается
незаполненной, Si может
отдать один электрон В,
а на его место придет
электрон от другого атома
Пустое место (дырка) может перемещаться по решетке
37.
Ec∆Е
Eа
Ev
В запрещенной зоне вблизи потолка
валентной зоны появляется
примесный акцепторный уровень
38.
Движение электрона вкристалле
В кристалле на электрон действует
поле кристаллической решетки
Поведение электронов в кристалле
похоже на поведение свободных
электронов
Их называют квазисвободными
39.
Эффективная массаэлектрона
Эффективная масса учитывает
взаимодействие электрона с
кристаллической решеткой и позволяет
описывать его движение теми же
уравнениями, что и свободный электрон
2
m 2
2
E ki
*
i
P k
k - Волновой вектор
40.
Для свободного электронаm0- масса электрона
p2
E
2m0
dE 2 2 k
dk 2m0
p k
2k 2
E
2m0
d 2E 2
2
dk
m0
2
mi* 2
E ki2
Для свободного электрона
эффективная масса равна
массе электрона
2
m0 2
d E
dk 2
m0 mi*













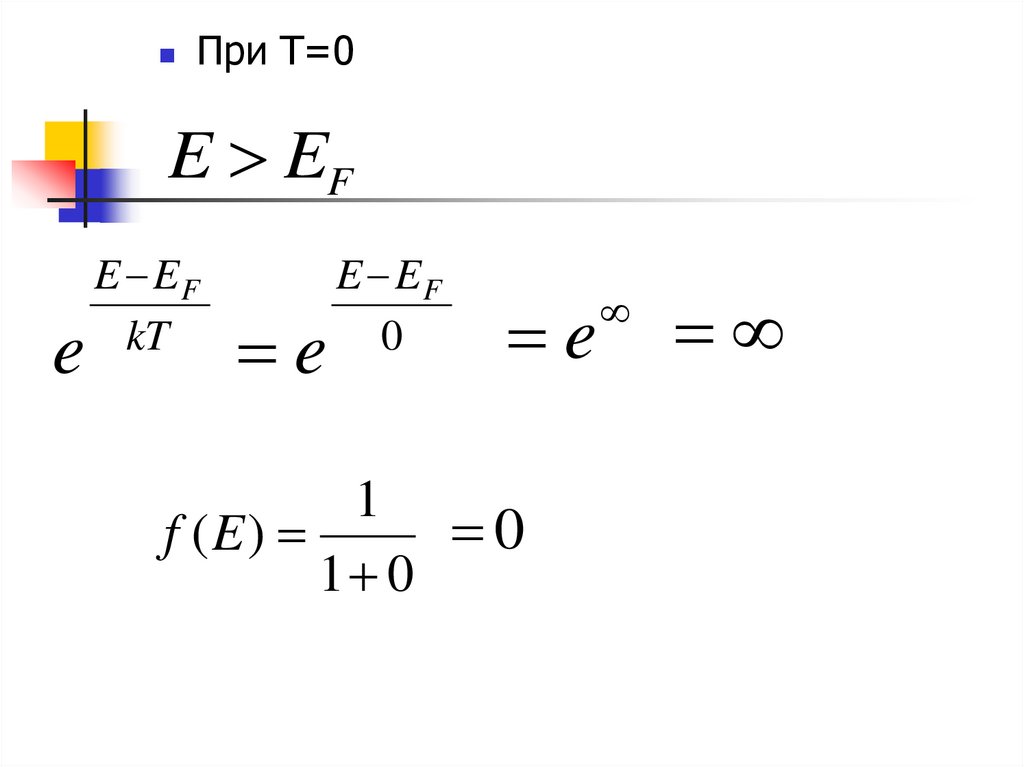
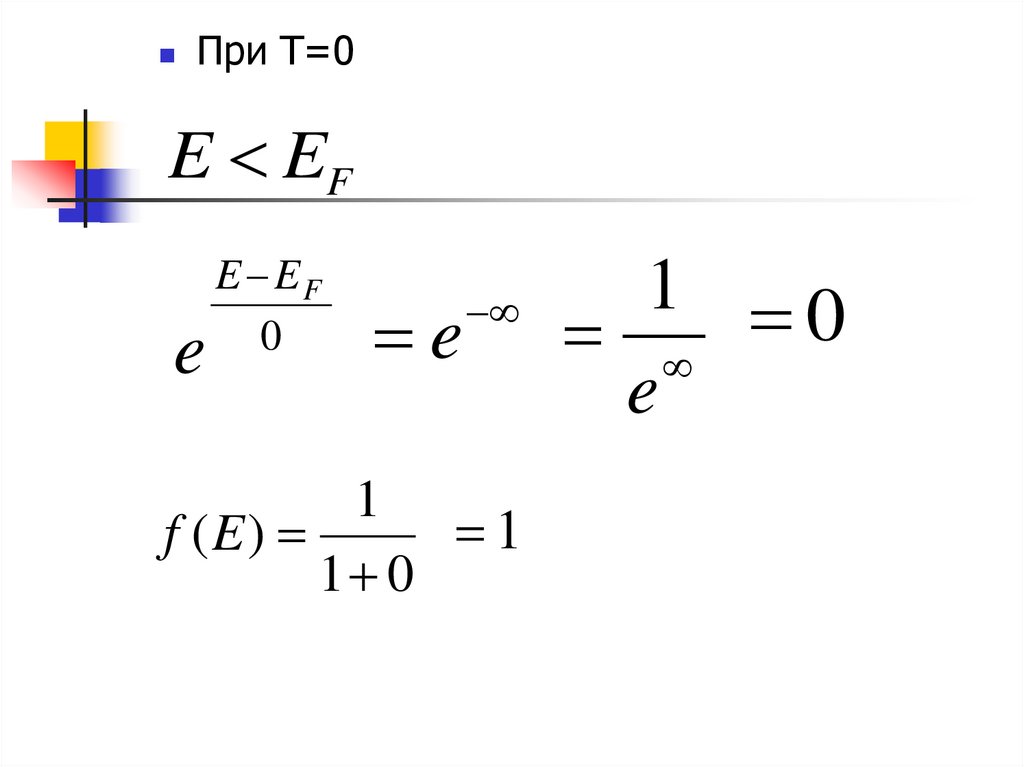

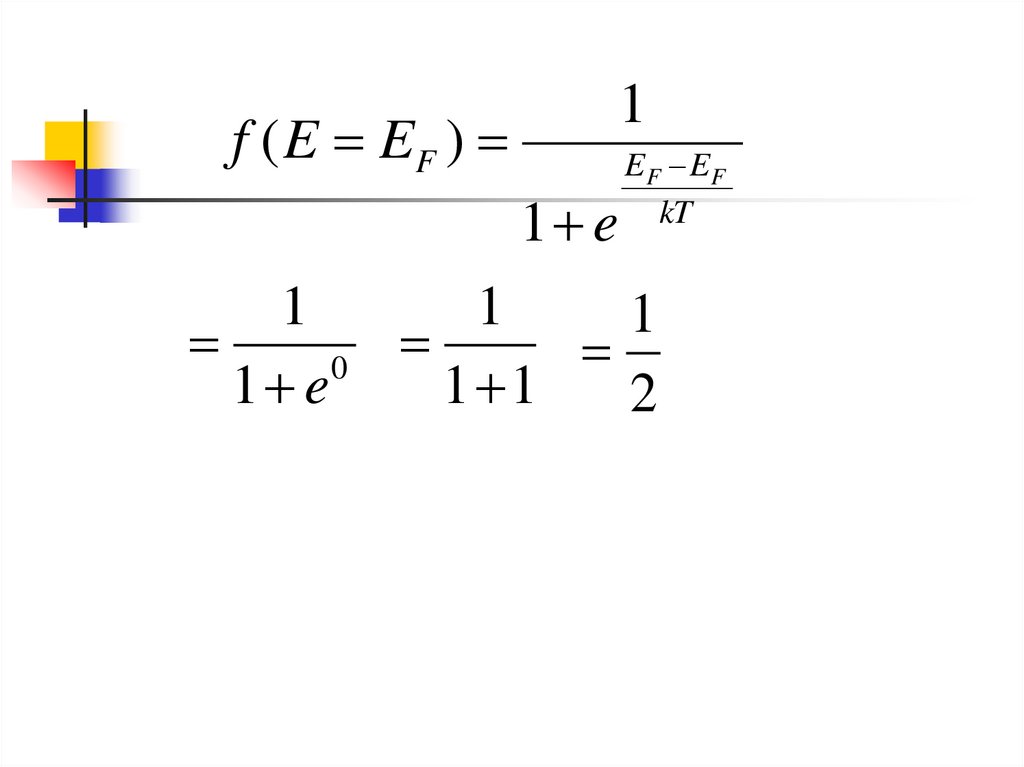


















 physics
physics








