Similar presentations:
Статистическая физика. Квантовая статистика. Физика. 2 курс. 4 семестр
1.
Физика. 2 курс. 4 семестрСпециалитет
Лекция 13. Статистическая физика
Квантовая статистика
- Статистика Ферми-Дирака
- Статистика Бозе-Эйнштейна
В.И. Читайкин
кандидат физико-математических наук
доцент
2.
План лекцииНаименование раздела, параграфа
Номер
слайда
Наименование раздела, параграфа
Номер
слайда
Введение
3
Раздел 3. Статистика Бозе-Эйнштейна
17
Раздел 1. Основные положения квантовой статистики
4
3.1. Постановка задачи
18
5
3.2. Распределение Бозе-Эйнштейна (формула)
19
6
3.3. Распределение Бозе-Эйнштейна (сравнительные
графики)
20
1.1. О неразличимости тождественных квантовых частиц
1.2. Замечание о границе между классической и
квантовой статистиками
1.3. Симметрия волновой функции
7
1.4. Бозоны и фермионы
8
1.4.1. Уточнённый принцип Паули
8
1.5. Иллюстрации
9
Раздел 2. Статистика Ферми-Дирака
10
2.1. Постановка задачи
11
2.2. Распределение Ферми-Дирака (формула и график)
12
2.3. Электронный газ
13
2.4. Энергия Ферми
14
2.4.1. Температура Ферми
14
2.5. Уравнение состояния электронного газа
15
2.5.1. Замечание о вырожденном электронном газе
15
2.6. Иллюстрация
16
3.4. Иллюстрации
21
2
3.
ВведениеВ 13-ой лекции продолжается краткое рассмотрение основ статистической физики для
системы, состоящей из огромного числа частиц.
В предыдущей, 12-ой лекции, рассматривалась классическая статистика, основанная на
предположении, что траекторию каждой частицы можно рассчитать и отследить. Если частиц
много, то надо лишь применить всё более мощные компьютеры и более прецизионные средства
измерения. Считается, что частицы одинаковые, но каждую из них можно различить и
перенумеровать. Соответствующее распределение таких частиц по импульсам (или по скоростям)
и о координатам в классической статистике – это распределение Максвелла-Больцмана.
В квантовой физике такое «самоуверенное» представление о частицах, а именно о том, что
их можно все учесть, траектории их рассчитать и измерить, отсутствует полностью. Поэтому для
квантовых частиц надо применять свою, квантовую статистику.
В разделе 1 лекции 13 изложены основные положения квантовой статистики и их отличие от
основных положений классической статистики.
Раздел 2 лекции 13 – это основные уравнения квантовой статистики Ферми-Дирака для
квантовых частиц – фермионов.
Раздел 3 лекции 13 – это основные уравнения квантовой статистики Бозе-Эйнштейна для
квантовых частиц – бозонов.
3
4.
Раздел 1. Основные положения квантовой статистики4
5.
1. Основные положения квантовой статистики1.1. О неразличимости тождественных квантовых частиц
Классическая статистика предполагает: множество частиц (например, газ) состоит из одинаковых
частиц, для которых известны координаты и скорость, а, значит, можно проследить или рассчитать
траекторию каждой из них. Классические частицы индивидуальны.
Квантовая статистика предполагает: множество частиц состоит из одинаковых частиц, но
координаты и скорость их не могут быть известны с точностью, достаточной, чтобы проследить или
рассчитать траекторию отдельной частицы из-за принципа неопределённостей Гейзенберга. Понятие
конкретной частицы теряет смысл, как и понятие траектории её движения. Квантовые частицы не
имеют индивидуальности, различить их невозможно.
Определение: тождественные квантовые микрочастицы – это частицы, имеющие одинаковые
физические характеристики. Например, электроны тождественны, т.к. все они обладают одинаковыми
значениями массы, заряда и спина.
Утверждение (принцип): тождественные квантовые микрочастицы
(ψ1)2
(ψ2)2
неразличимы в фазовом пространстве координат q и импульсов p, т.е.
в пространстве, для которого справедлив принцип неопределённостей
Гейзенберга – см. на рисунке справа.
Действительно, в области максимума пересекающихся вероятностей для первой (ψ1)2
и второй (ψ2)2 частиц различить эти частицы нельзя. Они слились воедино (пунктирная линия).
х
5
6.
1. Основные положения квантовой статистики1.2. Замечание о границе между классической и квантовой статистиками
Граница между классической и квантовой статистикой может быть выражена в единицах постоянной
Планка, т.к. этот вопрос напрямую связан с соотношением неопределённостей Гейзенберга.
Действительно, неопределённости основных фазовых параметров каждой частицы (Δх и Δр) таковы,
что их произведение должно быть:
Δх∙Δр ≥ h (соотношение неопределённостей Гейзенберга).
Такие неопределённости являются фундаментальными, основными.
В системе из множества частиц можно оценить среднюю неопределённость во взаимном положении
ближайших частиц как по координатам (Δх'), так и по импульсам (Δр'), т.е. в фазовом пространстве. Эти
величины определяются в каждом конкретном случае. По сути, величины Δх' и Δр' – это «расстояние» между
соседними частицами в фазовом пространстве.
Из опыта анализа квантовых систем следует: если произведение неопределённостей координат (Δх')
и импульсов (Δр') во взаимном положении множества частиц в фазовом пространстве таково, что:
1). Δх'∙Δр' ≈ (1 … 10)∙h, – то «работает» квантовая статистика (квантовые системы: электронные
облака в атомах, электронный газ в металлах, нуклонная жидкость в ядрах, сильно сжатый газ и др.).
2). Δх'∙Δр' ≥ 100∙h, – то следует пользоваться классической статистикой, квантовые эффекты
несущественны (частицы: большие молекулы, кластеры, пылинки и т.д.).
В промежуточной области 10∙h ≤ Δх'∙Δр' ≤ 100∙h требуется тщательное рассмотрение каждой
конкретной ситуации.
6
7.
1. Основные положения квантовой статистики1.3. Симметрия волновой функции
Вернёмся к квантовой статистике, предварительно, конечно, убедившись, что она применима в
конкретном рассматриваемом случае.
Каждая квантовая частица в отдельности характеризуется соответствующей волновой функцией
ψ(ξ) = ψ(q,p), где q – совокупность пространственных координат частицы, p – совокупность импульсов
частицы; ξ – совокупность всех координат в фазовом пространстве ξ = {q, p}.
Рассмотрим две квантовые частицы, каждая из которых имеет свои фазовые координаты:
ξ1 = {q1, p1} и ξ2 = {q2, p2}.
Очевидно, что если поменять частицы местами, то вероятность обнаружить их останется прежней –
в силу их тождественности и неразличимости. Это означает, что
[ψ(ξ1,ξ2)]2 = [ψ(ξ2,ξ1)]2 , - сделана перестановка фазовых координат ξ1 и ξ2.
Извлечём квадратный корень:
ψ(ξ1,ξ2) = ± ψ(ξ2,ξ1), т.е. возможны оба знака: «+» и «-».
Определение: если при перестановке частиц 1↔2 волновая функция ψ(ξ1,ξ2):
- не меняет знак: ψ(ξ1,ξ2) = ψ(ξ2,ξ1), то она – симметричная волновая функция;
- меняет знак: ψ(ξ1,ξ2) = - ψ(ξ2,ξ1), то она – антисимметричная волновая функция.
7
8.
1. Основные положения квантовой статистики1.4. Бозоны и фермионы
Симметрия волновой функции квантовой частицы определяется её спином.
Частица с целым или нулевым спином описывается симметричной волновой функцией. Такая
частица называется бозон. Примеры бозонов: фотон, пи-мезон и другие элементарные частицы.
Частица с полуцелым спином описывается антисимметричной волновой функцией. Такая частица
называется фермион. Примеры фермионов: электрон, протон, нейтрон и ряд элементарных частиц.
Наибольший интерес в рамках нашего курса представляет фермион – электрон, т.к. именно электрон определяет характер
химических взаимодействий.
1.4.1 Уточнённый принцип Паули (1925 год)
«В одном и том же атоме не может быть двух фермионов – частиц с полуцелым спином, в частности,
электронов, обладающих одинаковой совокупностью квантовых чисел».
Другими словами, фермионы, в том числе, электрон, могут находиться в квантовых состояниях
только поодиночке.
Для бозонов с целым или нулевым спином принцип Паули неприменим, поэтому бозоны могут и
«любят» накапливаться в одном и том же квантовом состоянии.
Фермионы (электроны) – «индивидуалисты», бозоны (фотоны) – «коллективисты».
8
9.
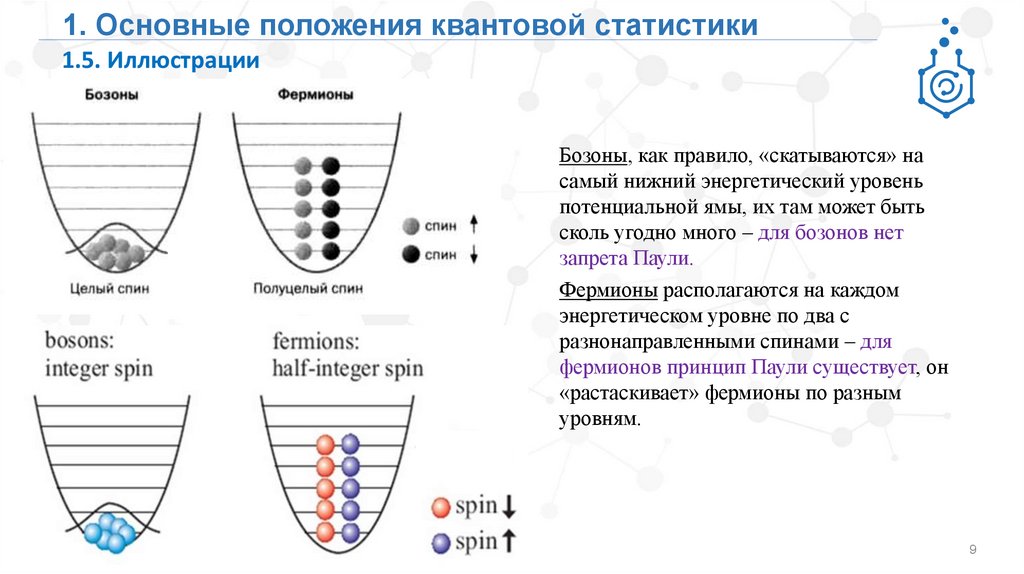
1. Основные положения квантовой статистики1.5. Иллюстрации
Бозоны, как правило, «скатываются» на
самый нижний энергетический уровень
потенциальной ямы, их там может быть
сколь угодно много – для бозонов нет
запрета Паули.
Фермионы располагаются на каждом
энергетическом уровне по два с
разнонаправленными спинами – для
фермионов принцип Паули существует, он
«растаскивает» фермионы по разным
уровням.
9
10.
Раздел 2. Статистика Ферми-Дирака(статистика фермионов)
10
11.
2. Статистика Ферми-Дирака2.1. Постановка задачи
Одна из основных задач статистической физики, как классической, так и квантовой – это
нахождение распределения частиц по импульсам (скоростям). В классической статистике – это
распределение Максвелла (точнее, Максвелла-Больцмана) – см. лекцию 12.
Задача: найти законы распределения квантовых частиц (фермионов и бозонов) по импульсам.
Напомню, 6N-мерное пространство N частиц, образованное совокупностью координат {x,y,z} и
проекций импульсов {px,py,pz}, называется фазовым пространством. В классической статистике
элементарный объём этого пространства, т.е. для одной частицы (элементарная ячейка):
dV = {dx,dy,dz, dpx,dрy,dpz} может быть сколь угодно малым.
В квантовой статистике из-за действия соотношения неопределённостей Гейзенберга элементарная
ячейка ограничена снизу: dVmin = {dx,dy,dz, dpx,dрy,dpz} ~ h3. Покажите это самостоятельно.
Второе отличие квантовой статистики от классической: на фермионы (электроны, протоны и др.)
действует принцип (запрет) Паули. Ситуацию с бозонами обсудим в следующем разделе 3.
В остальном вывод формулы распределения для фермионов и бозонов аналогичен выводу формулы
для классических частиц.
Полезно: Физически простой, но математически громоздкий вывод формул для квантовых частиц (фермионов и бозонов)
содержится в учебнике И.В.Савельева, том 5, параграф 7.1. В издании 2019 года, из-во «Лань» – том 3, часть 3, глава 7, параграф
11
34. При выводе используются понятия микросостояний, вероятности и энтропии – см. лекцию 12.
12.
2. Статистика Ферми-Дирака2.2. Распределение Ферми-Дирака (формула и график)
Предварительное замечание: Традиционно распределение квантовых частиц записывается в виде распределения по энергиям –
в отличие от распределения классических частиц: по импульсам или по скоростям. Нетрудно преобразовать распределение по
импульсам в распределение по энергиям. Сделайте это самостоятельно, например, применительно к распределению Максвелла.
Формула распределения фермионов по энергии Е (распределение Ферми-Дирака):
Т – температура всей совокупности фермионов, например, температура электронного газа
k – постоянная Больцмана
μ – химический потенциал или энергия Ферми ЕF, максимальная энергия
фермионов (электронов) – уровень Ферми.
График распределения Ферми-Дирака:
График необычен.
1. При нулевой температуре (Т=0) – это строгий прямоугольник,
резко обрывающийся при Е=ЕF, т.е. фермионов (электронов) с
энергией выше уровня Ферми не существует – сплошная линия.
2. По мере повышения температуры резкая граница
«размывается», появляются фермионы (электроны) с энергией
выше энергии Ферми EF – пунктирная линия.
12
13.
2. Статистика Ферми-Дирака2.3. Электронный газ
Электронный газ – это совокупность электронов в одной квантовой системе. Например, свободные
электроны в металлах образуют электронный газ.
Распределение электронов по энергии в электронном газе – это распределение среднего числа
электронов на определённом уровне энергии, которое с учётом спина электрона (два состояния: ± 1/2 ,
т.к. электрон, как фермион, антисимметричная частица) записывается так:
Обозначения ε и εF – это немного другое обозначение энергии Е и
энергии Ферми ЕF
При нулевой температуре (Т=0):
- если ε < εF →
2
- если ε > εF →
0
Проверьте это самостоятельно.
При любой температуре, включая Т=0:
- если ε = εF →
1
Упрощенный образ: Электронный газ – это, по сути, идеальный газ невзаимодействующих частиц,
но с существенно иным распределением частиц (электронов) по энергиям, чем в распределении
13
Максвелла.
14.
2. Статистика Ферми-Дирака2.4. Энергия Ферми
Энергия Ферми ЕF или химический потенциал μ (другое название) рассчитываются через
концентрацию электронов n:
Обратите внимание: в формуле используется постоянная Планка h (без черты).
Напишите формулу с перечёркнутой постоянной Планка ℏ.
Для свободных электронов в металле характерное значение концентрации составляет n ≈ 10 28…29 м-3,
тогда ЕF(T=0) = 5 эВ.
2.4.1. Температура Ферми
Температура Ферми определяется традиционно, с использованием связи температуры и энергии:
Е = kТ.
Тогда, температура Ферми ТF, соответствующая энергии Ферми ЕF, рассчитывается так:
TF = EF / k.
Для свободного электронного газа в металле с ЕF = 5 эВ температура Ферми составляет 60000К(!).
14
15.
2. Статистика Ферми-Дирака2.5. Уравнение состояния электронного газа
Уравнение состояния связывает энергию газа с его температурой: E = f(T).
Для классических частиц: Е =
N – число частиц;
температура Т задаётся в энергетических единицах (как правило, в эВ).
Полезно вспомнить: уравнение состояния для идеального газа – это уравнение Клапейрона-Менделеева: PV = f(T).
Произведение давления на объём характеризует энергию газа.
Для квантовых частиц фермионов (электронов) уравнение состояния выглядит так:
Т – температура (эВ)
ЕF – энергия Ферми (эВ)
Эта формула «работает» при низких температурах: T < TF , напомню, что TF ~ десятки тысяч градусов.
При высоких температурах (T > TF ) квантовое уравнение состояние переходит в классическое.
2.5.1. Замечание о вырожденном электронном газе
Электронный газ при низких температурах T < TF (или kT < EF) называется вырожденым.
При высоких температурах T > TF (или kT > EF) электронный газ называется невырожденым.
Следствие: при практически значимых температурах, не превышающих, как правило, несколько тысяч
градусов, электронный газ в металле – вырожденный. Вспомните, чему равна температура Ферми в металле (п.2.4). 15
16.
2. Статистика Ферми-Дирака2.6. Иллюстрация
Образ (условный) электронного газа в металле
Напишите – что есть что на картинке слева:
Что есть что на картинке справа:
чёрные шары?, синие шарики?, белесые полосы?
яркие фонари?, туман в воздухе?
Кому установлен памятник?, где это место?
16
17.
Раздел 3. Статистика Бозе-Эйнштейна(статистика бозонов)
17
18.
3. Статистика Бозе-Эйнштейна3.1. Постановка задачи
Задача: найти закон распределения квантовых частиц – бозонов по импульсам, точнее, по энергии.
Вывод формулы распределения бозонов совершается точно так же, как и для фермионов.
Напомню: физически простой, но математически громоздкий вывод формул для квантовых частиц (фермионов и бозонов)
содержится в учебнике И.В.Савельева, том 5, параграф 7.1. В издании 2019 года, из-во «Лань» – том 3, часть 3, глава 7, параграф
34. При выводе используются понятия микросостояний, вероятности и энтропии – см. лекцию 12.
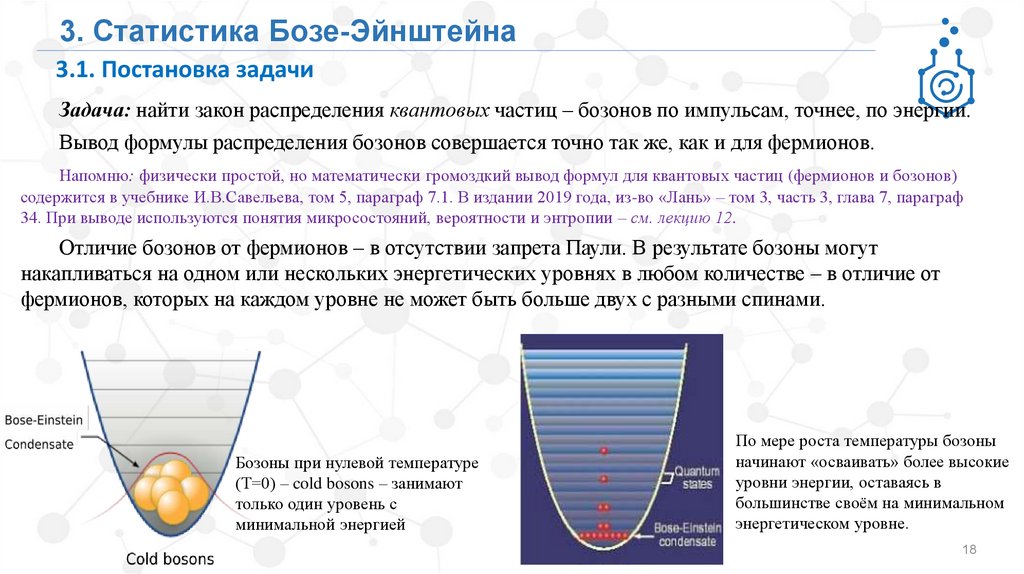
Отличие бозонов от фермионов – в отсутствии запрета Паули. В результате бозоны могут
накапливаться на одном или нескольких энергетических уровнях в любом количестве – в отличие от
фермионов, которых на каждом уровне не может быть больше двух с разными спинами.
Бозоны при нулевой температуре
(Т=0) – cold bosons – занимают
только один уровень с
минимальной энергией
По мере роста температуры бозоны
начинают «осваивать» более высокие
уровни энергии, оставаясь в
большинстве своём на минимальном
энергетическом уровне.
18
19.
3. Статистика Бозе-Эйнштейна3.2. Распределение Бозе-Эйнштейна (формула)
Формула распределения бозонов по энергии Е (распределение Бозе-Эйнштейна):
Т – температура всей совокупности бозонов
k – постоянная Больцмана
μ – химический потенциал
Для наиболее интересного с точки зрения приложений бозона – фотона (спин = 0) значение
химического потенциала μ = 0. Формула распределения Бозе-Эйнштейна существенно упрощается –
получите сами.
Характерной особенностью бозонов с нулевым химическим потенциалом является непостоянство
их количества в системе. Такие бозоны (фотоны) могут поглощаться и излучаться стенками системы
или другими частицами, находящимися в ней, например, электронами.
Для сравнения: Для фермионов несохранение числа частиц в системе категорически невозможно.
19
20.
3. Статистика Бозе-Эйнштейна3.3. Распределение Бозе-Эйнштейна (сравнительные графики)
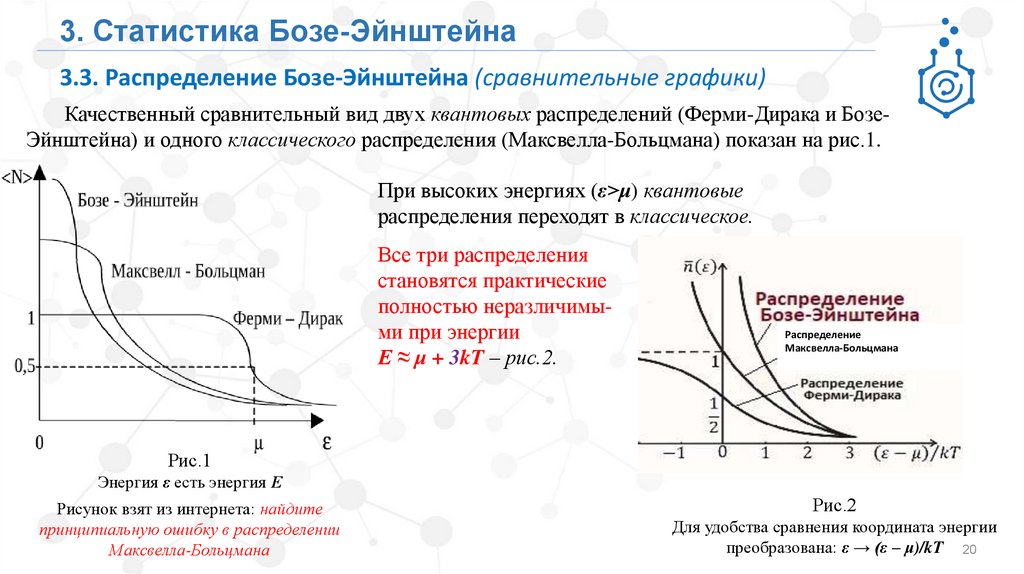
Качественный сравнительный вид двух квантовых распределений (Ферми-Дирака и БозеЭйнштейна) и одного классического распределения (Максвелла-Больцмана) показан на рис.1.
При высоких энергиях (ε>μ) квантовые
распределения переходят в классическое.
Все три распределения
становятся практические
полностью неразличимыми при энергии
Е ≈ μ + 3kT – рис.2.
Распределение
Максвелла-Больцмана
Рис.1
Энергия ε есть энергия Е
Рисунок взят из интернета: найдите
принципиальную ошибку в распределении
Максвелла-Больцмана
Рис.2
Для удобства сравнения координата энергии
преобразована: ε → (ε – μ)/kT 20
21.
3. Статистика Бозе-Эйнштейна3.4. Иллюстрации
Показаны результаты математического моделирования применительно к одному из наиболее интересных
бозонов – бозону Хиггса, откалиброванные на эксперимент.
21
Рождение бозона Хиггса
Траектория движение бозона Хиггса в Большом Адронном Коллайдере, ЦЕРН, Швейцария



















 physics
physics








