Similar presentations:
Лекция 24 (7). Квантовые статистики
1. Квантовые статистики
ВоГУЛекция 24 (7)
Квантовые статистики
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
1
2. План
23.
Квантовая статистикаКвантовая статистика изучает состояние систем, состоящих
из большого числа квантовых частиц
Любое состояние частицы характеризуется набором
квантовых чисел, полностью определяющих это состояние
Набор таких состояний дискретен; их можно пронумеровать
i – номер состояния;
Еi – энергия частицы в i–том состоянии;
Ni – число частиц системы, находящихся в i–том
состоянии.
Ni называется числом заполнения i–того состояния.
Если N – полное число частиц системы, то N равно сумме
чисел заполнения по всем состояниям:
N Ni
i
4.
Частицы подчиняются разным статистическимзакономерностям в зависимости от того, имеют частицы
целый или полуцелый спин
Существование двух статистик связано с:
свойствами их волновых функций
принципом неразличимости тождественных частиц
Квадрат модуля волновой функции определяет плотность
вероятности найти частицу в данной точке:
dp
dV
2
Квадрат модуля не должен меняться при перестановке
тождественных частиц
x1, x2 x2 , x1
2
2
5.
x1, x2 x2 , x12
2
У этого уравнения два решения:
x1, x2 x2 , x1
x1, x2 x2 , x1
Волновая функция частиц с
целым спином симметрична
относительно перестановки
частиц
Волновая функция частиц с
полуцелым спином
антисимметрична
относительно перестановки
частиц
статистика Бозе-Эйнштейна
бозоны
статистика Ферми-Дирака
фермионы
6.
Принцип Паулиx1, x2 x2 , x1
Фермионы
Принцип Паули справедлив только для частиц с полуцелым
спином (фермионов)
Если две частицы находятся в одинаковом состоянии, их
волновая функция не может менять знак при перестановке
частиц
Расширенная формулировка принципа Паули может быть такой:
У фермионов волновая функция антисимметрична
относительно перестановки частиц
Отсюда вытекает невозможность двум фермионам находиться в
одинаковом состоянии
Фермионы – «индивидуалисты»
Число заполнения – 0 или 1 (состояние пусто или занято).
7.
x1, x2 x2 , x1Бозоны
Бозоны, напротив, «коллективисты»:
вероятность того, что при добавлении в систему
нового бозона он займёт состояние с номером i,
пропорциональна корню из числа заполнения этого
состояния:
pi ~ Ni
Число заполнения состояния – любое
Запрет Паули не действует
8.
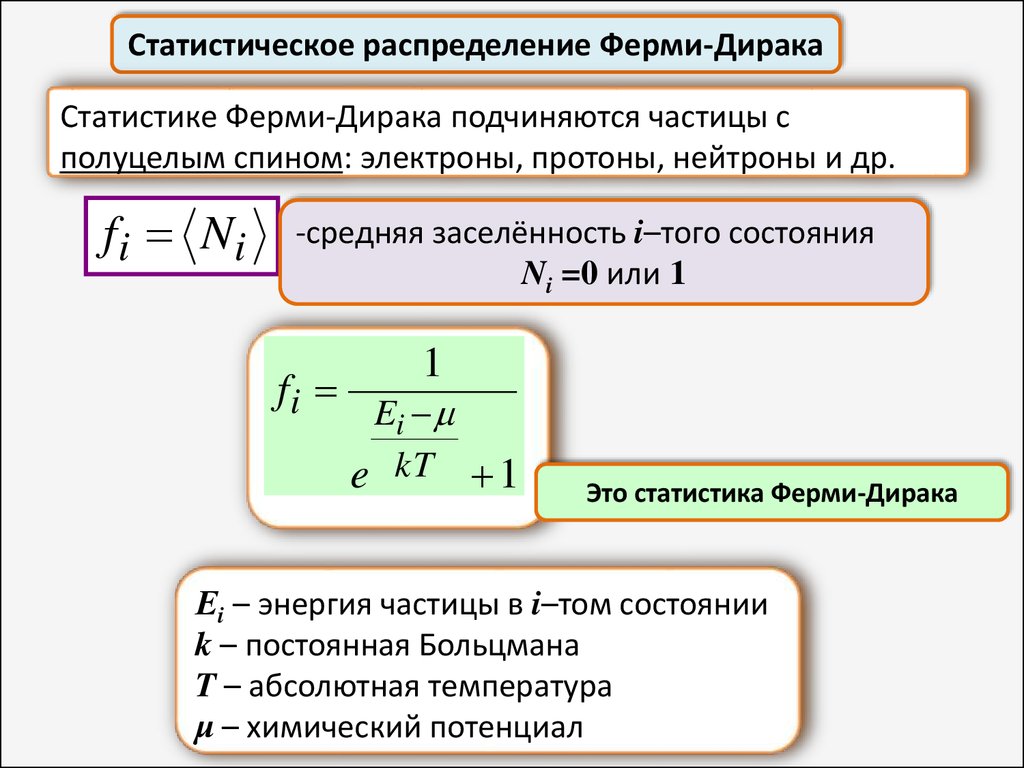
Статистическое распределение Ферми-ДиракаСтатистике Ферми-Дирака подчиняются частицы с
полуцелым спином: электроны, протоны, нейтроны и др.
f i Ni
-средняя заселённость i–того состояния
Ni =0 или 1
fi
1
Ei
e kT 1
Это статистика Ферми-Дирака
Еi – энергия частицы в i–том состоянии
k – постоянная Больцмана
T – абсолютная температура
μ – химический потенциал
9.
fi1
Ei
e kT 1
По определению:
Химический потенциал μ – это увеличение энергии
системы при добавлении в неё одной частицы
dE
dN
Для фермионов химический потенциал всегда
положителен: μ>0
Химический потенциал зависит от числа частиц в системе
и температуры
10.
Статистика Ферми-ДиракаВычислим функцию f(E) при T→0
Если E<μ, то:
E
kT
E
exp
0
kT
1
f E
1
E
exp
1
kT
fi
1
Ei
e kT 1
Если E>μ, то:
E
kT
E
exp
kT
1
0
E
exp
1
kT
f E 0
11.
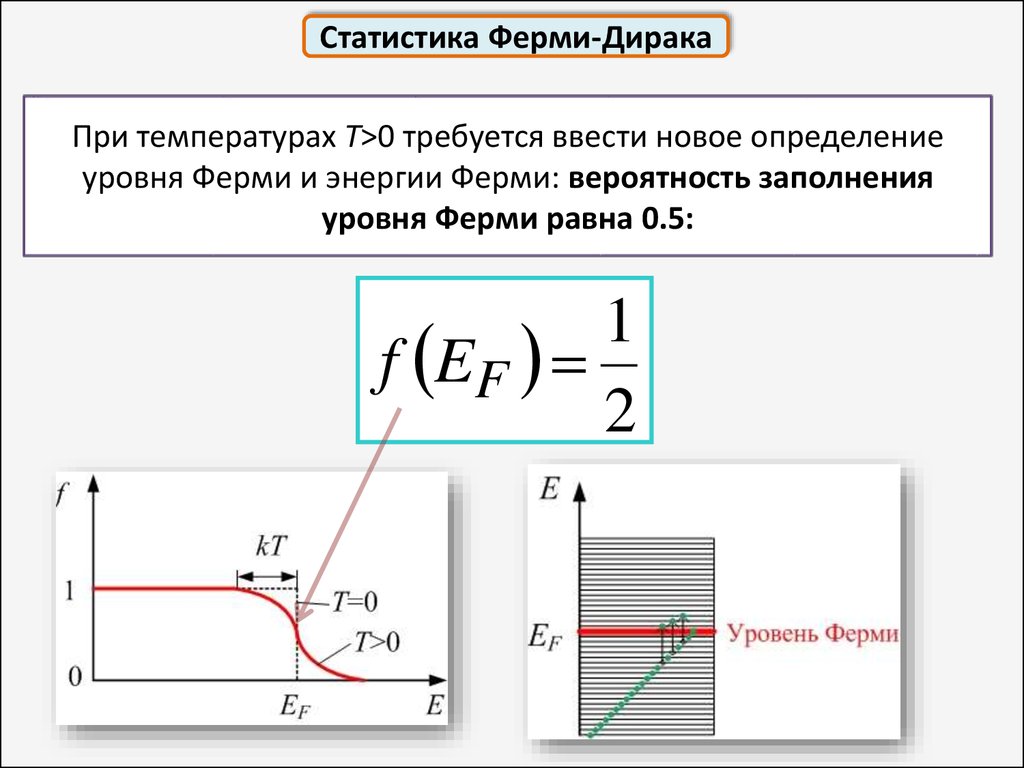
Статистика Ферми-ДиракаЕсли E<μ, то
f E 1
Если E>μ, то
f E 0
f
Все состояния ниже уровня Ферми заняты;
выше - свободны
1
E
e kT 1
12.
Смысл химического потенциала для фермионов:μ - это максимальная энергия, которую может иметь
частица при абсолютном нуле
Соотвествующая энергия называется энергией Ферми, а
энергетический уровень – уровень Ферми
EF
13.
EFЗапрет Паули заставляет частицы «взбираться» вверх по энергетическим
уровням
При абсолютном нуле энергия системы минимальна; сначала заполняются
состояния с минимальной энергией, а наивысший занятый уровень – это
уровень Ферми
Все уровни ниже него заняты: N=1, f=1; выше него – свободны: N=0, f=0
Уровень Ферми при абсолютном нуле – это наивысший занятый уровень.
Энергия Ферми зависит от количества частиц: чем их больше, тем большее
число уровней будет занято и выше окажется последний занятый уровень.
2
2
h 3n 3
EF
8m
14.
Температура Ферми TFОпределение:
kTF EF
EF
TF
k
2
2
h 3n 3
EF
8m
Из-за запрета Паули температура Ферми при больших
концентрациях частиц может быть очень большой
Для металлов концентрация электронов
n=1029 м-3 → TF=106 К
15.
Статистика Ферми-Диракаdν – количество квантовых
состояний в узком диапазоне
энергий от E до E+dE
Плотность квантовых состояний
g(E) – число состояний, приходящихся на
единичный интервал энергий:
Плотность квантовых состояний g(E) возрастает
с увеличением энергии:
если глубина потенциальной ямы конечна, то
чем выше, тем ближе уровни энергии
расположены друг к другу:
Без доказательства:
3
V 2m 2
g (E) 2
E
2
2
4
d ( E )
g (E)
dE
16.
Статистика Ферми-ДиракаЧисло электронов dN, находящихся в
состояниях с энергией от E до E+dE:
d ( E )
g (E)
dE
3
V 2m 2
g (E) 2
E
4 2 2
3
1
V 2m 2
dN ( E ) f E g ( E ) dE
E dE
2
2
E
exp
1 2
kT
Короче, при E<μ и T→0:
dN
~ E
dE
17.
Статистика Ферми-ДиракаЧисло электронов dN, находящихся в состояниях с энергией E
до E+dE, в расчёте на единичный интервал энергий,
при E<μ и T→0:
dN
~ E
dE
18.
Статистика Ферми-ДиракаПри температурах T>0 распределение «расплывается» в
интервале энергий порядка kT вблизи уровня Ферми
Электроны, находящиеся вблизи
уровня Ферми, за счёт тепловой
энергии поднимаются выше на
свободные уровни
19.
Статистика Ферми-ДиракаПри температурах T>0 требуется ввести новое определение
уровня Ферми и энергии Ферми: вероятность заполнения
уровня Ферми равна 0.5:
1
f E F
2
20.
Статистика Бозе-ЭйнштейнаСтатистическому распределению Бозе-Эйнштейна подчиняюся
частицы с целым спином (бозоны)
Число заполнения состояния Ni может принимать любые
значения, так как запрету Паули бозоны не подчиняются.
Примеры частиц – бозонов:
фотоны, (спин s=1)
фононы (спин s=0)
Фонон – это квант колебаний кристаллической решётки
Энергия упругих волн, распространяющихся в кристалле, квантуется
Фонон – минимальная порция этой энергии
Фонон – квазичастица, или, точнее, не совсем частица, или совсем даже не
частица: распространение упругих волн в кристалле удобно описывать так,
как будто это перемещаются частицы – фононы, имеющие определённую
энергию и импульс
21.
Статистика Бозе-ЭйнштейнаДля частиц с целым спином:
f Ei
1
Ei
e kT 1
Химический потенциал для бозонов μ≤0
Конкретно для фотонов и фононов μ=0
Если число частиц в системе не сохраняется (фотоны и фононы
могут поглощаться или рождаться), то химический потенциал
для таких частиц равен нулю
При сверхнизких температурах все частицы находятся в
одинаковом основном состоянии с минимальной энергией
(запрет Паули этому не мешает), следовательно, полная
энергия Бозе-газа может быть очень мала
22.
Статистика Ферми-Диракаf E
1
E
e kT 1
Спин - полуцелый
Статистика Бозе-Эйнштейна
f E
1
E
e kT 1
Спин - целый
23.
Вырожденный и невырожденный газОпределение:
Газ называется вырожденным, если его свойства отличаются от свойств
классического газа, то есть нельзя использовать классическую статистику
(Больцмана), а нужно учитывать квантовые свойства газа
Если
Ei
exp
1
kT
f Ei
1
Ei
e kT 1
, обе статистики можно записать:
1
Ei
Ei
Ei
e kT e kT A e kT
e kT
это – классическая статистика Больцмана
24.
Вырожденный и невырожденный газОбе квантовые статистики при определённых условиях переходят в
классическую статистику Больцмана:
получается классический идеальный газ
E
f A e kT
Квантовые свойства нужно учитывать при низких
температурах и больших концентрациях частиц
Определение:
2
2 n 3
TB
3 m k
- температура вырождения
При T<TB газ вырожденный (квантовый)
при T>TB газ невырожденный (классический)
25.
2n 3
TB
3 m k
Вырожденный и невырожденный газ
Примеры: В полупроводниках концентрация
электронов n=1018 м-3
2
TB 10 4 K
T>TB → электронный газ в полупроводнике – классический, невырожденный
В металлах концентрация электронов n=1029 м-3
TB 104 K
Температура вырождения превышает любую температуру, при которой
металл обычно используется
В металле электронный газ вырожденный
Это значит, что лишь небольшая доля электронов с энергией, близкой к
энергии Ферми, возбуждается за счёт теплового движения и переходит на
вышележащие уровни
Следовательно, в тепловом движении участвует лишь небольшая доля
электронов, и теплоёмкость металла определяется колебаниями
кристаллической решётки, а электроны практически не участвуют в
теплоёмкости
26.
Фотонный газ2
n 3
TB
3 m k
m 0 TB
Фотонный газ всегда вырожден
Фотоный газ – Бозе-газ, так как спин фотона – целый:
sγ=1
Химический потенциал
μγ=0
1
f
Энергия фотона Eγ=hν, и тогда
2
h
e kT 1
27.
Фононный газФонон – квазичастица; квант колебаний
кристаллической решётки
Упругие волны имеют квантовые свойства; энергия
фонона равна
E=hν
Фононый газ – Бозе-газ, так как спин фонона – целый: s=0
Химический потенциал μ=0
f
1
h
e kT 1
28.
Фононный газ. Температура ДебаяДлина упругой волны в кристалле не может быть меньше межатомных
расстояний d
Только при λ>d волна распространяется как бы в сплошной среде:
λmin=d
Если υ – скорость распространения упругих волн в кристалле, то
максимальная частота фонона:
max
энергия фонона:
min
h h
E h max
min
d
Определение: Характеристическая температура Дебая T соответствует
D
фононам с максимальной энергией:
h
TD
k d
h
k TD
d
kTD h max
29.
Теплоёмкость кристаллической решёткиОсновной вклад в теплоёмкость твёрдого тела вносит
энергия тепловых колебаний частиц, находящихся в узлах
кристалличнской решётки
Для металлов некоторый вклад вносит также
вырожденный электронный газ, но этот вклад не очень
большой, и вопрос о теплоёмкости электронного газа
здесь рассматриваться не будет
30.
Теплоёмкость кристаллической решётки1) Классическая теория
По теореме о равнораспределении энергии по степеням свободы на
одну степень свободы приходится в среднем энергия, равная
Число колебательных степени свободы i=3
При колебаниях:
E1
k T k T
2
2
Кинетическая
энергия
Энергия одного атома (иона):
k T
E1
2
Потенциальная
энергия
Eатома i kT 3kT
Внутренняя энергия одного моля кристалла, состоящего из NА частиц
(химически простое тело):
U m N А Eатома N А 3kT 3RT
31.
Теплоёмкость кристаллической решёткиU m 3RT
Молярная теплоёмкость:
1) Классическая теория
dU m
CV
3R
dT
Молярная теплоёмкость всех химически простых тел одинакова, не
зависит от температуры и равна:
Дж
CV 3R 25
Это – закон Дюлонга и Пти:
моль К
Для химических соединений число частиц в одном моле вещества в z раз
больше (z – число атомов в молекуле)
Пример: в моле NaCl содержится NА атомов натрия и NА атомов хлора; z=2
CV 3Rz
32.
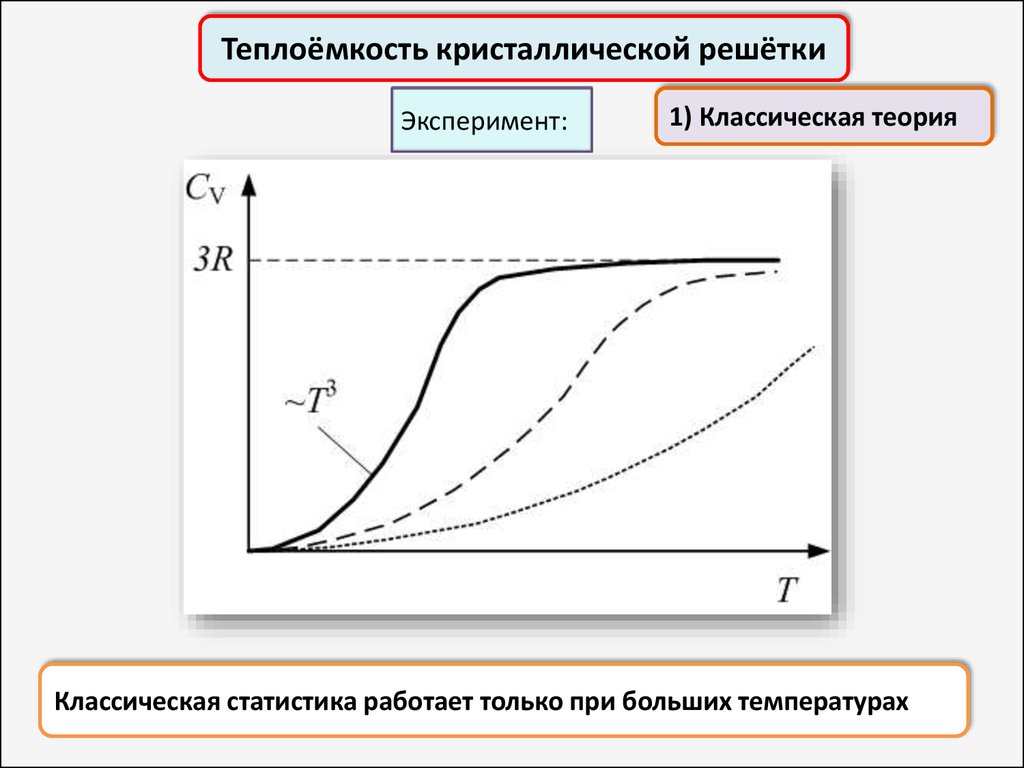
Теплоёмкость кристаллической решёткиЭксперимент:
1) Классическая теория
Классическая статистика работает только при больших температурах
33.
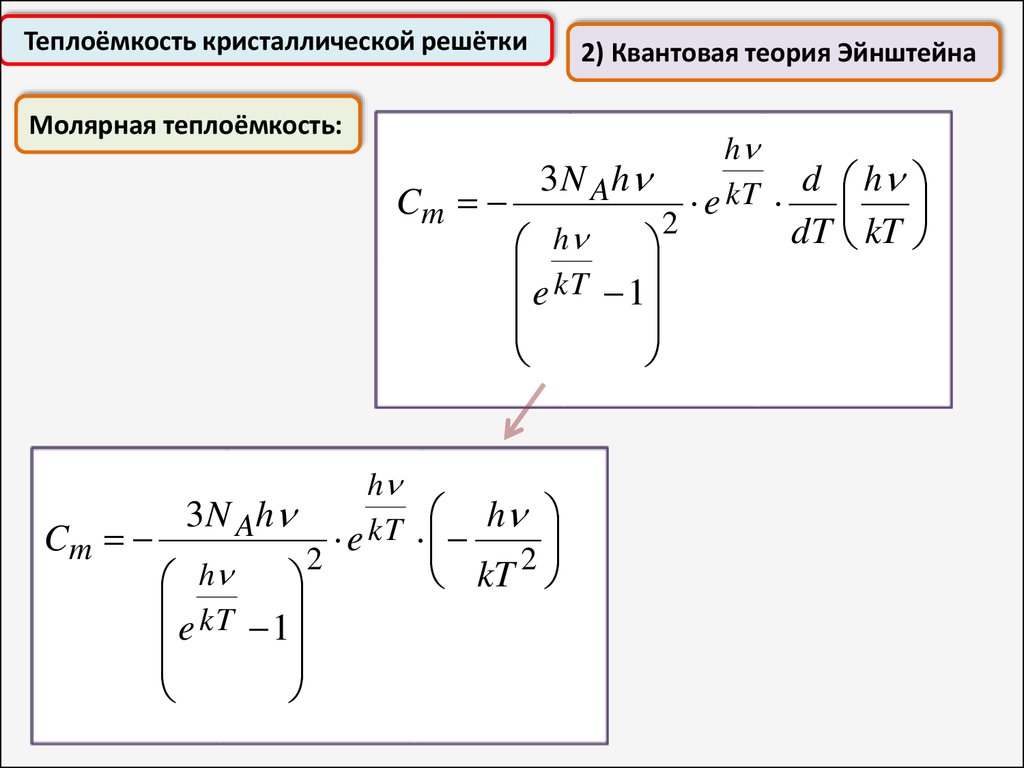
Теплоёмкость кристаллической решётки2) Квантовая теория Эйнштейна
Кристалл рассматривается как система независимых квантовых
осцилляторов
Средняя энергия, приходящаяся на одну степень свободы квантового
осциллятора с частотой ν, равна:
E 1
h
h
e kT 1
h
2
энергия нулевых колебаний
Внутренняя энергия одного моля химически простого вещества:
3 N Ah
Число колебательных
степеней свободы
U m 3N A E 1
h
e kT 1
3 N Ah
2
34.
Теплоёмкость кристаллической решётки3 N Ah
U m 3N A E 1
h
e kT 1
2) Квантовая теория Эйнштейна
3 N Ah
2
Молярная теплоёмкость по определению:
Cm
3 N A h
2
h
kT
e 1
молярная нулевая
энергия (const)
dU m
Cm
dT
h
d h
kT
e
dT kT
35.
Теплоёмкость кристаллической решётки2) Квантовая теория Эйнштейна
Молярная теплоёмкость:
Cm
3 N A h
2
h
kT
e 1
h
h
3 N A h
kT
Cm
e
2
2
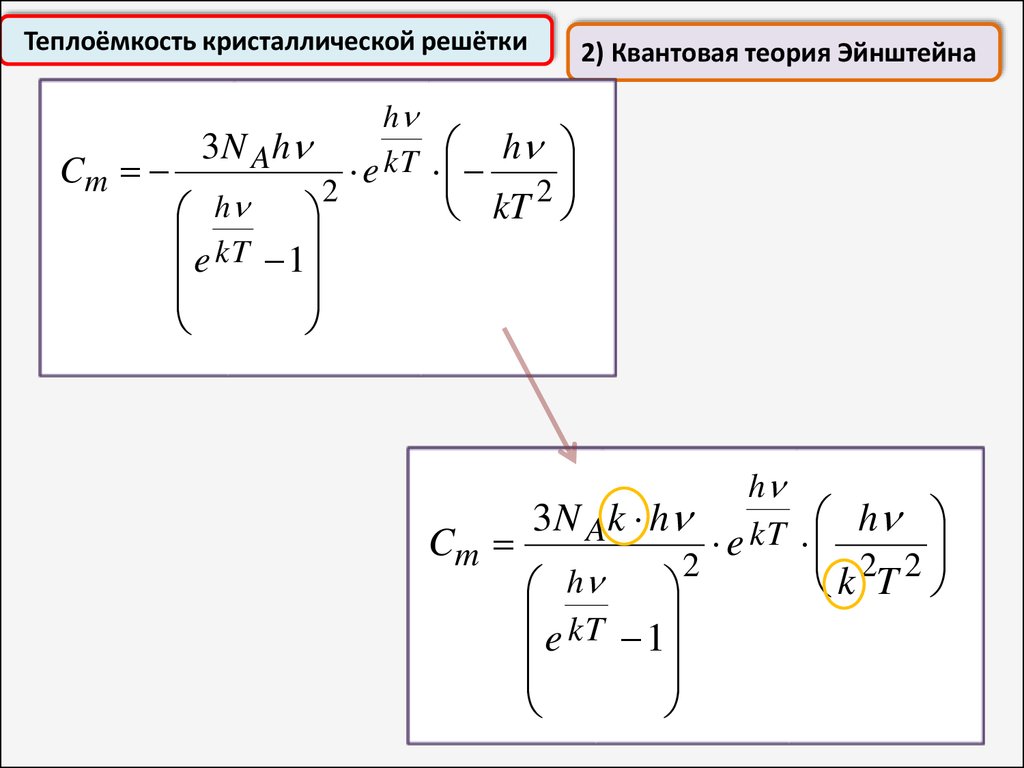
h
kT
kT
e 1
h
d h
kT
e
dT kT
36.
Теплоёмкость кристаллической решётки2) Квантовая теория Эйнштейна
h
h
3 N A h
kT
Cm
e
2
2
kT
h
kT
e 1
h
3 N Ak h kT h
Cm
e
2
2 2
h
kT
e 1
k T
37.
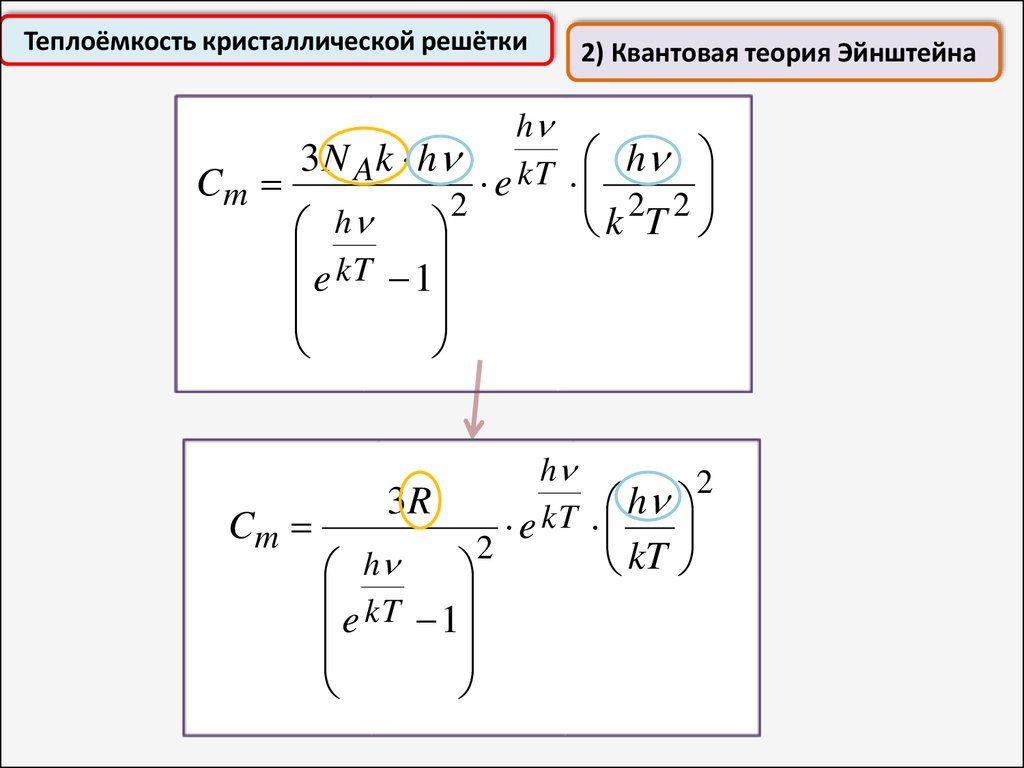
Теплоёмкость кристаллической решётки2) Квантовая теория Эйнштейна
h
3 N Ak h kT h
Cm
e
2
2
2
h
k T
kT
e 1
Cm
3R
2
h
kT
e 1
h
2
h
kT
e
kT
38.
Теплоёмкость кристаллической решёткиCm
3R
2
h
kT
e 1
Определение:
2) Квантовая теория Эйнштейна
h
2
h
e kT
kT
kTE h
TE – характеристическая температура Эйнштейна
2
TE
eT
TE
Cm 3R
2
T TE
T
e 1
39.
Теплоёмкость кристаллической решётки2
TE
eT
T
Cm 3R E
2
T TE
T
e 1
2) Квантовая теория Эйнштейна
При высоких температурах теория
Эйнштейна даёт то же, что и
классическая теория:
T
TE
TE
T
TE
e 1 1 T 1 T
TE
TE
2
TE e T
T 3R e 0 3R
Cm 3R
3
R
e
T TE 2
T
40.
Теплоёмкость кристаллической решётки2
TE
eT
2) Квантовая теория Эйнштейна
При низких температурах теория
Эйнштейна даёт то же, что и
классическая теория:
T
Cm 3R E
2
T TE
T
e 1
T 0
2
2
TE
eT
TE
Cm 3 R
T TE
T
e
2
TE
3R
T
0
TE
eT
Теория Эйнштейна даёт качественное согласие поведения
теплоёмкости, но не даёт количественного согласия:
зависимость C~T3 в теории Эйнштейна не получается
41.
Теплоёмкость кристаллической решётки3) Квантовая теория Дебая
Дебай учёл взаимодействие квантовых осцилляторов и
получил хорошее согласие с экспериментом
Результат, полученный Дебаем при низких температурах:
T TD
3
T
12 R
T
234 R
Cm
5 TD
TD
4
3
Cm ~ T
3
42.
Электропроводимость металлов(выводы квантовой теории)
Квантовая теория электропроводимости металлов, основывающаяся на
статистике Ферми-Дирака, даёт удельную электропроводимость металлов:
концентрация электронов
проводимости в металле
средняя длина свободного
пробега электронов,
имеющих энергию Ферми
ne F
m * uF
2
эффективная масса
электрона
средняя скорость теплового
движения электронов,
имеющих энергию Ферми
43.
Электропроводимость металлов(выводы квантовой теории)
ne F
m * uF
2
По классической теории электропроводимости:
ne
2m u
2
44.
Электропроводимость металлов(выводы квантовой теории)
ne F
m * uF
2
Эффективная масса m* может очень сильно отличаться от реальной массы
электрона и даже быть отрицательной
Понятие эффективной массы вводится для того, чтобы автоматически
учесть действие на электрон периодического поля кристаллической
решётки Eреш.:
F e E E реш.
m * a e E
ma e E E реш.
m * a ma e E реш.
45.
Электропроводимость металлов(выводы квантовой теории)
ne2 F
m * uF
Движению электрона в металле сопоставляется волновой процесс
(волны де Бройля)
Идеальная регулярная кристаллическая решётка с неподвижными
ионами электронные волны не рассеивает; то есть не оказывает
сопротивления движению электронов
Электронные волны рассеиваются на неоднородностях
(нерегулярностях) решётки – атомах примесей, дефектах, а также на
тепловых колебаниях ионов
Электронные волны рассеиваются на фононах – квантах колебаний
кристаллической решётки
Причина сопротивления металлов – неоднородности
решётки и тепловые колебания ионов
46.
Электропроводимость металлов(выводы квантовой теории)
ne2 F
m * uF
В квантовой теории средняя скорость теплового движения электронов
Ферми не зависит от температуры: изменение температуры мало влияет
на электроны, находящиеся вблизи уровня Ферми, поскольку энергия
Ферми много больше энергии теплового движения:
E F kT
С увеличением температуры возрастает рассеяние электронных волн на
фононах, уменьшается средняя длина свободного пробега электронов:
1
F ~
T
1
~ F ~
T
47.
Электропроводимость металлов(выводы квантовой теории)
1
~ F ~
T
Удельное сопротивление:
1
~T
0 T
удельное
сопротивление
при 0о С
0 1 t
температурный коффициент сопротивления
1
1
град K
48.
Электропроводимость металлов(выводы квантовой теории)
0 T
При уменьшении температуры
сопротивление металлов
уменьшается, так как
уменьшается рассеяние
электронных волн на тепловых
колебаниях ионов, и при T→0
стремится к некоторому
значению – остаточному
сопротивлению, связанному с
примесями и дефектами
кристаллической решётки
49.
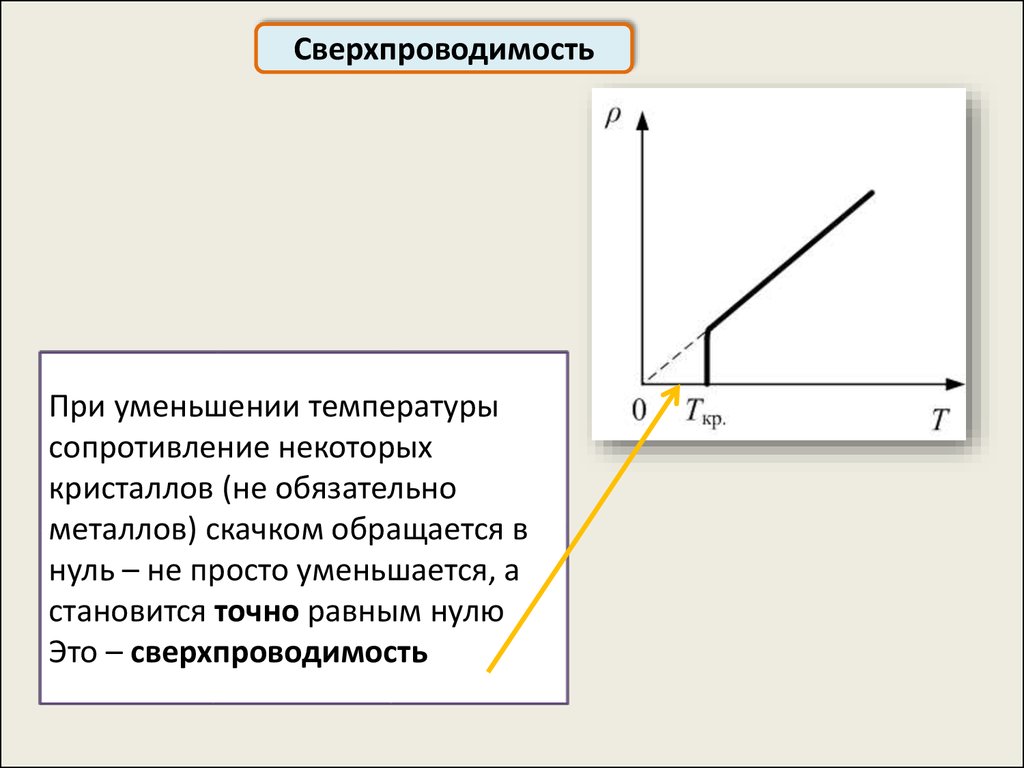
СверхпроводимостьПри уменьшении температуры
сопротивление некоторых
кристаллов (не обязательно
металлов) скачком обращается в
нуль – не просто уменьшается, а
становится точно равным нулю
Это – сверхпроводимость
50.
СверхпроводимостьСверхпроводимость была открыта в 1911 г. КамерлингОннесом в экспериментах с ртутью
При сверхнизких температурах ртуть теряла свое
сопротивление
Критическая температура (температура, при которой
сопротивление исчезает) для ртути равна Ткр.=4.15 К
Было установлено, что лучшие по электрическим
параметрам проводники – платина, золото, медь – не
являются сверхпроводниками
51.
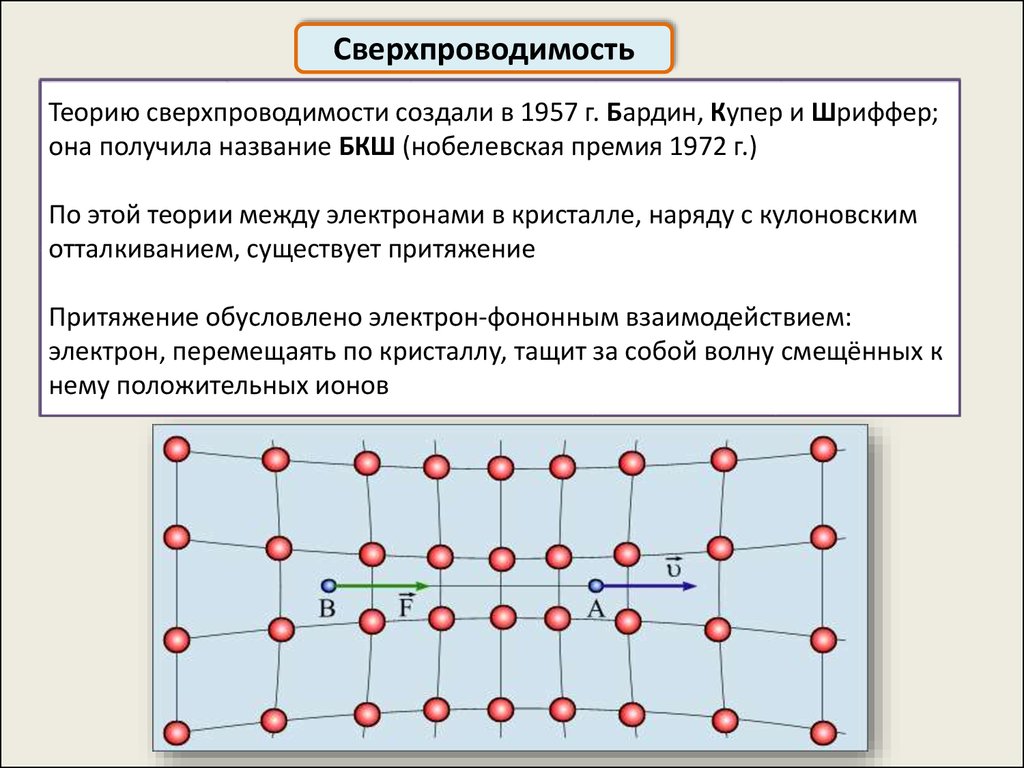
СверхпроводимостьТеорию сверхпроводимости создали в 1957 г. Бардин, Купер и Шриффер;
она получила название БКШ (нобелевская премия 1972 г.)
По этой теории между электронами в кристалле, наряду с кулоновским
отталкиванием, существует притяжение
Притяжение обусловлено электрон-фононным взаимодействием:
электрон, перемещаять по кристаллу, тащит за собой волну смещённых к
нему положительных ионов
52.
СверхпроводимостьВ результате между двумя электронами возникает эффективный
положительный заряд сдвинутых ионов решётки, и к этому заряду
притягиваются электроны
Два электрона образуют связанное состояние – «куперовскую» пару
Размеры пары в 104 раз превышают межатомные расстояния
Между электронами пары есть много других электронов
Два электрона могут образовать пару только в том случае, если их
спины противоположны
Поэтому куперовская пара имеет спин, равный нулю, а значит, это –
бозон; подчиняется статистике Бозе-Эйнштейна, а запрет Паули на
бозоны не распространяется
53.
СверхпроводимостьВ одном и том же квантовом состоянии может находиться любое число
частиц
Бозоны проявляют «стремление» к объединению, то есть тем интенсивнее
заселяют данное состояние, чем больше частиц в этом состоянии уже
находится
При сверхнизких температурах происходит бозе-конденсация: куперовские
пары занимают самое нижнее энергетическое состояние
Находясь на нижнем энергетическом уровне, куперовские пары не могут
отдавать энергию, так как она у пары минимальная, меньше быть не может
Не могут куперовские пары и принять
энергию, если она меньше, чем 2ΔЕ
(в расчёте на один электрон пары – ΔЕ)
ΔЕ – расстояние до ближайшего
разрешённого уровня от основного,
где сконденсировались
куперовские пары
54.
СверхпроводимостьЭлектроны сверхпроводника, объединённые в куперовские пары,
образуют единое целое квантовое состояние
Они ведут себя как единая квантовая система
Куперовские пары образуют когерентное, «коллективное», состояние, в
котором все они имеют один и тот же импульс
Можно сказать, что они образуют квантовую сверхтекучую жидкость
Эта когерентность электронов в
большом масштабе –
макроскопическая демонстрация
квантовых принципов
55.
СверхпроводимостьБлагодаря такому «единению» электроны проводимости без потерь
энергии, а следовательно, и без сопротивления, могут протекать через
кристаллическую решетку вещества
Электроны, объединенные в куперовские пары, перестают
взаимодействовать как между собой, так и с кристаллической решеткой
Это и есть отсутствие сопротивления у проводника
(физической природой омического сопротивления является обмен
энергией между носителями заряда и кристаллической решеткой)
Сверхпроводящее состояние исчезает, когда при повышении температуры
средняя энергия теплового движения kТ превысит ΔЕ, так как
разрушаются все куперовские пары и электроны переходят на более
высокие энергетические состояния
56.
СверхпроводимостьВ теории сверхпроводимости
интервал энергии ΔЕ носит
специфическое название –
«энергетическая щель»
Куперовские пары образуют
основное (наиболее выгодное с
энергетической точки зрения)
состояние сверхпроводника
На энергетической шкале оно располагается в узкой области в окрестности
уровня Ферми EF
Остальные электронные состояния отделены энергетической щелью ΔE.
57.
СверхпроводимостьТеория БКШ объясняет, почему хорошие проводники, такие, как медь и
золото, не являются сверхпроводниками
Электроны проводимости в этих веществах легко проходят сквозь атомную
решетку, почти не взаимодействуя с ней
Это делает такие материалы хорошими электрическими проводниками,
поскольку в них теряется мало энергии из-за рассеяния решеткой
Для достижения же сверхпроводящего состояния необходимо сильное
взаимодействие между атомами решетки и электронами
По этой причине очень хорошие проводники электричества, как правило,
не бывают сверхпроводниками
58.
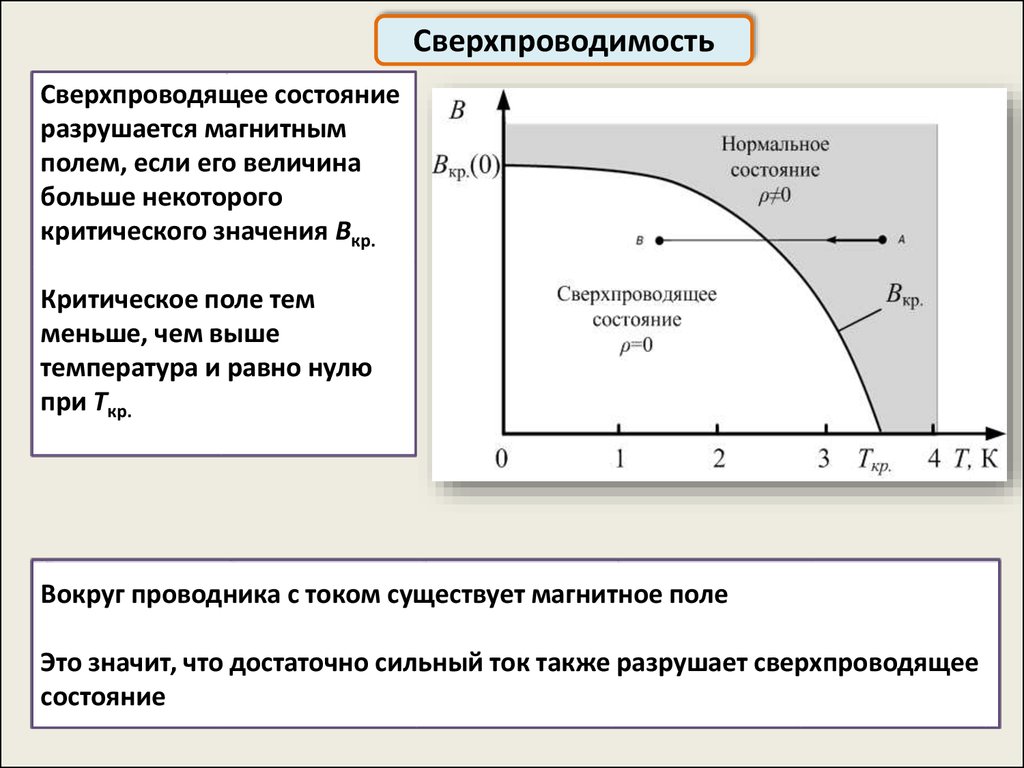
СверхпроводимостьСверхпроводящее состояние
разрушается магнитным
полем, если его величина
больше некоторого
критического значения Вкр.
Критическое поле тем
меньше, чем выше
температура и равно нулю
при Ткр.
Вокруг проводника с током существует магнитное поле
Это значит, что достаточно сильный ток также разрушает сверхпроводящее
состояние
59.
Сверхпроводимость. Эффект МейснераОткрыт в 1933 г.
Не очень сильное магнитное
поле (меньше Вкр.) выталкивается
из сверхпроводящего образца,
то есть сверхпроводники
являются идеальными
диамагнетиками
60.
Сверхпроводимость. Эффект МейснераЭффект Мейснера связан с тем, что при В<Вкр. в поверхностном слое
сверхпроводящего образца появляется круговой незатухающий ток, сила
которого как раз такова, что магнитное поле этого тока компенсирует
внешнее поле в толще сверхпроводника
Опыт показывает, что в случае больших
образцов слабое магнитное поле в
условиях эффекта Мейснера проникает
в металл на глубину d~10-5÷10-6 см;
именно в этом слое течёт
поверхностный ток
61.
Сверхпроводимость. Эффект МейснераЭффект Мейснера объясняет «левитацию» магнита над сверхпроводником,
охлаждаемым жидким азотом: магнитное поле выталкивается из
сверпроводника, поэтому возникает такое же отталкивание, как между
магнитом и любым диамагнетиком
62.
СверхпроводимостьЕсть ещё один эффект: квантование магнитного потока
Если придать сверхпроводнику форму кольца, то в нем будет циркулировать
незатухающий ток
В момент перехода проводника в сверхпроводящее состояние внешнее
магнитное поле сосредотачивается внутри выреза кольца
Установлено, что величина захваченного магнитного потока может принимать
только значения, кратные Ф0= hc/q:
hc
0
q
где q – заряд носителей сверхпроводящего тока
Оказалось, что q=2e
Это подтверждает предположение о куперовском спаривании электронов.
63.
Высокотемпературная сверхпроводимостьВ 1986 г. был открыт сплав, сверхпроводящие свойства которого
сохраняются и при 30 K (высокотемпературная сверхпроводимость)
Сегодня уже известны материалы, остающиеся сверхпроводниками даже
при 160 К, то есть выше температуры жидкого азота, с которым работать
значительно легче и дешевле, чем с жидким гелием
При этом общепринятой теории, которая объясняла бы этот класс
высокотемпературной сверхпроводимости, до сих пор не создано, но ясно,
что в рамках теории БКШ ее объяснить невозможно
64.
Высокотемпературная сверхпроводимостьВ основе теоретической модели высокотемпературной сверхпроводимости
(ВТСП), разработанной академиком В.Л. Гинзбургом, лежит так называемый
экситонный механизм взаимодействия электронов
Дело в том, что в электронной системе существуют особые волны – экситоны
Подобно фононам, описывающим тепловые колебания решетки, экситоны
являются квазичастицами, перемещающимися по кристаллу, и не
связанными с переносом электрического заряда и массы
Такой сверхпроводник, например, представляет собой металлическую
пленку в слоях диэлектрика или полупроводника
Электроны проводимости, движущиеся в металле, отталкивают электроны
диэлектрика, то есть окружают себя облаком избыточного положительного
заряда, который и приводит к образованию электронной пары
65.
Высокотемпературная сверхпроводимостьТакой механизм предсказывает высокие значения критической
температуры. Открытие сверхпроводника с комнатной критической
температурой означало бы большую экономию: ведь потери на «джоулево
тепло» составляют почти 30% от вырабатываемой в мире электроэнергии
Есть ещё одна неприятность, связанная с высокотемпературной
сверхпроводимостью: высокотемпературные сверхпроводники – это
керамические соединения: они хрупкие, их нельзя спаять или изготовить из
них длинный гибкий провод
66.
Высокотемпературная сверхпроводимостьРеальное использование сверхпроводников началось в 50-х − начале 60-х
годов XX века
В настоящее время работают сверхпроводящие магниты различных размеров
и форм. Их применение вышло за рамки чисто научных исследований, и
сегодня они широко используются в лабораторной практике, в ускорительной
технике, томографах, установках для управляемой термоядерной реакции
Наибольшее применение сверхпроводники нашли в настоящее время в
области создания сильных магнитных полей
Современная промышленность производит из сверхпроводников
разнообразные провода и кабели, используемые для изготовления обмоток
сверхпроводящих магнитов, с помощью которых получают значительно более
сильные поля, чем при использовании железных магнитов
Сверхпроводящие магниты являются и более экономичными
67.
Высокотемпературная сверхпроводимостьЕще одно применение сверхпроводников − создание подшипников и опор
без трения
Если над металлическим кольцом с током поместить сверхпроводящую сферу,
то на ее поверхности в силу эффекта Мейснера индуцируется
сверхпроводящий ток, что приводит к появлению сил отталкивания между
кольцом и сферой, и сфера может повиснуть над кольцом
На этом может быть основано создание, например, новых видов транспорта.
Речь идет о создании поезда на магнитной подушке, в котором будут
полностью отсутствовать потери на трение о колею дороги
Модель такой сверхпроводящей дороги длиной 400 м была построенав
Японии еще в 1970-х годах. Расчеты показывают, что поезд на магнитной
подушке сможет развивать скорость до 500 км/ч. Такой поезд будет «зависать»
над рельсами на расстоянии 2−3 см
68.
Высокотемпературная сверхпроводимостьПрименений сверхпроводимости может привести к созданию сверхбыстрых
электронно-вычислительных машин
Речь идет о так называемых криотронах − переключающих сверхпроводящих
элементах
Такие устройства могут легко сочетаться со сверхпроводящими
запоминающими элементами
69.
Сверхпроводимость и сверхтекучестьСверхпроводящее состояние является макроскопическим квантовым
состоянием
Открытая в 1938 г. сверхтекучесть жидкого гелия – тоже макроскопический
квантовый эффект
Сверхтекучий гелий – это еще одна квантовая жидкость (первой
являются куперовские электронные пары)
Поэтому логично объяснить свойства сверхтекучего гелия на той же основе,
как и объяснение сверхпроводимости
70.
СверхпроводимостьЛевитация:
http://clipiki.ru/video/148657/sverhprovodimost
http://www.youtube.com/watch?v=tva4yTj-cpU
Сверхпроводимость (старый советсткий фильм):
http://www.youtube.com/watch?v=kDxD2d8dkpk
Высокотемпературная сверхпроводимость:
http://www.youtube.com/watch?v=anNvsGD5FUk
http://www.youtube.com/watch?v=wDGbzw2fSeg





























































 physics
physics








