Similar presentations:
Квантовая теория электропроводности. Электропроводность металлов. Лекция №8
1.
Лекция № 8КВАНТОВАЯ ТЕОРИЯ
ЭЛЕКТРОПРОВОДНОСТИ.
ЭЛЕКТРОПРОВОДНОСТЬ
МЕТАЛЛОВ
61
1
2.
ВОПРОСЫ23. Электроны в металлах. Функция
распределения Ферми-Дирака.
Энергия и уровень Ферми.
24. Элементы зонной теории
твердых тел. Металлы (проводники),
полупроводники и диэлектрики с
точки зрения зонной теории твердых
тел.
61
2
3.
25. Электросопротивление, еготемпературная зависимость.
Сверхпроводимость. Свойства
сверхпроводников.
Высокотемпературные
сверхпроводники.
61
3
4.
614
5.
23. Электроны в металлах.Функция распределения
Ферми-Дирака.
Энергия и уровень Ферми.
61
5
6.
В квантовой механике, как и вклассической статистической
физике, закономерности поведения
частиц имеют статистический и
вероятностный характер. Однако в
квантовой механике необходимость
статистического описания поведения
ансамбля частиц является
следствием корпускулярноволнового дуализма частиц материи,
открытого Луи де Бройлем.
61
6
7.
Квантовая теория для объясненияэлектропроводности металлов учла
все особенности новых свойств
электронов:
1) электрон отрицательно
заряженная частица
qe = 1,6 10- 19 Кл;
2) электрон имеет массу покоя
me = 9,11 10- 31 кг;
61
7
8.
3) заряд электрона инвариантен и независит от скорости движения;
4) электрон имеет двойственную
корпускулярно-волновую природу;
5) электрон относится к
тождественно-неразличимым
частицам;
6) электрон имеет собственный
момент импульса Lsz ≠ 0;
61
8
9.
7) электрон имеет спиновоемагнитное число
ms = 1/2 (спин S =1/2);
8) электроны имеют собственный
магнитный момент рms ≠ 0;
9) электроны описываются
статистикой Ферми-Дирака,
являются фермионами с полуцелым
спином.
61
9
10.
В квантовой механике состояниеэлектрона описывается набором
квантовых чисел: главное квантовое
число n = 1, 2, 3, ... ; характеризует
энергию электрона в атоме;
орбитальное квантовое число
ℓ = 0, 1, 2, 3, ... , n 1;
характеризует энергию
взаимодействия электронов;
61
10
11.
магнитное квантовое числоmℓ = 0, 1, 2, 3, ... , ℓ;
характеризует проекцию момента
импульса; спиновое квантовое число
mS = 1/2 ( спин S =1/2).
61
11
12.
При заполнении электронамиэнергетических состояний
(уровни энергии) для фермионов
выполняется принцип Паули:
В данной системе тождественных
фермионов любые два из них не
могут одновременно находиться в
одном и том же состоянии.
61
12
13.
Заполнение электронамиэнергетических уровней происходит
при одновременном выполнении
трех условий:
а) электроны должны иметь вполне
определенные значения квантовых
чисел: n, ℓ, mℓ, ms;
б) соответствовать минимуму
энергии;
в) подчиняться принципу запрета
Паули.
61
13
14.
Электронный газ(электроны проводимости)
находится в трёхмерной
потенциальной яме
(кристаллическая решётка).
В квантовой механике доказывается,
что энергия таких частиц может
иметь только дискретные
(квантовые) значения.
61
14
15.
Электроны являются фермионами(их спин равен ±½)
и их распределение по энергиям
описывается формулой
Ферми-Дирака:
1
ni
e
Wi WF
kT
61
1
15
16.
ni – среднее число частиц,приходящихся на одно квантовое
состояние,
k – постоянная Больцмана,
T – термодинамическая
температура,
Wi – энергия данного состояния,
WF – уровень Ферми
(максимально возможная энергия
при абсолютном нуле).
61
16
17.
Бозоны – частицы с целым спином,в некотором квантовом состоянии
может находиться неограниченное
число частиц.
Формула Бозе-Эйнштейна:
1
ni
e
Wi WF
kT
61
1
17
18.
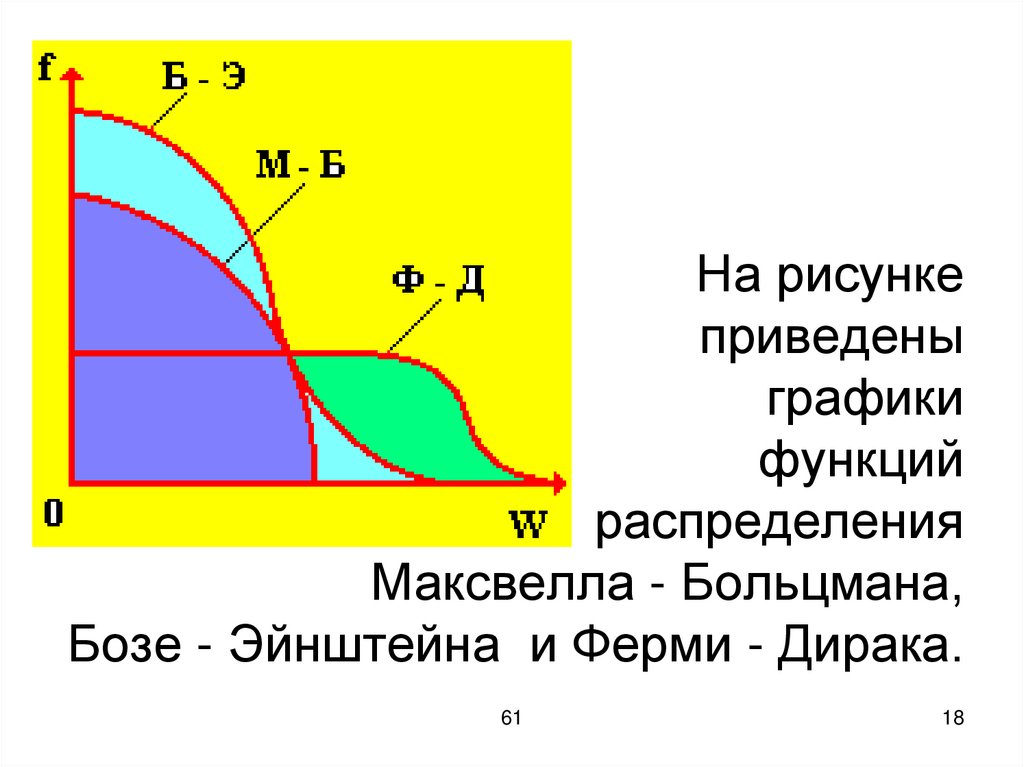
На рисункеприведены
графики
функций
распределения
Максвелла - Больцмана,
Бозе - Эйнштейна и Ферми - Дирака.
61
18
19.
При абсолютном нуле электронырасполагаются попарно на самых
низких, доступных для них уровнях.
ni 2,
ni 0,
n 1,
i
если
если
если
61
Wi WF ;
Wi WF ;
Wi WF .
19
20.
Энергия Фермипри абсолютном нуле:
2
2
h 3n 3
WF
2m 8π
h = 6,626·10–34 Дж·с – постоянная
Планка;
n ≈ 1028 – 1029 м–3 – концентрация
электронов.
61
20
21.
Температура Ферми:WF 0
TF
kБ
WF(0) = 5 эВ, TF ≈ 60 000 К.
61
21
22.
Средняя энергия электронов2
3
5π kT
W WF 1
5 12 WF
Средняя энергия (в эВ) свободных
электронов при абсолютном нуле
3
3
W WF 5 3
5
5
Чтобы классическому электрону
сообщить такую энергию, его нужно
нагреть до 25 000 К.
61
22
23.
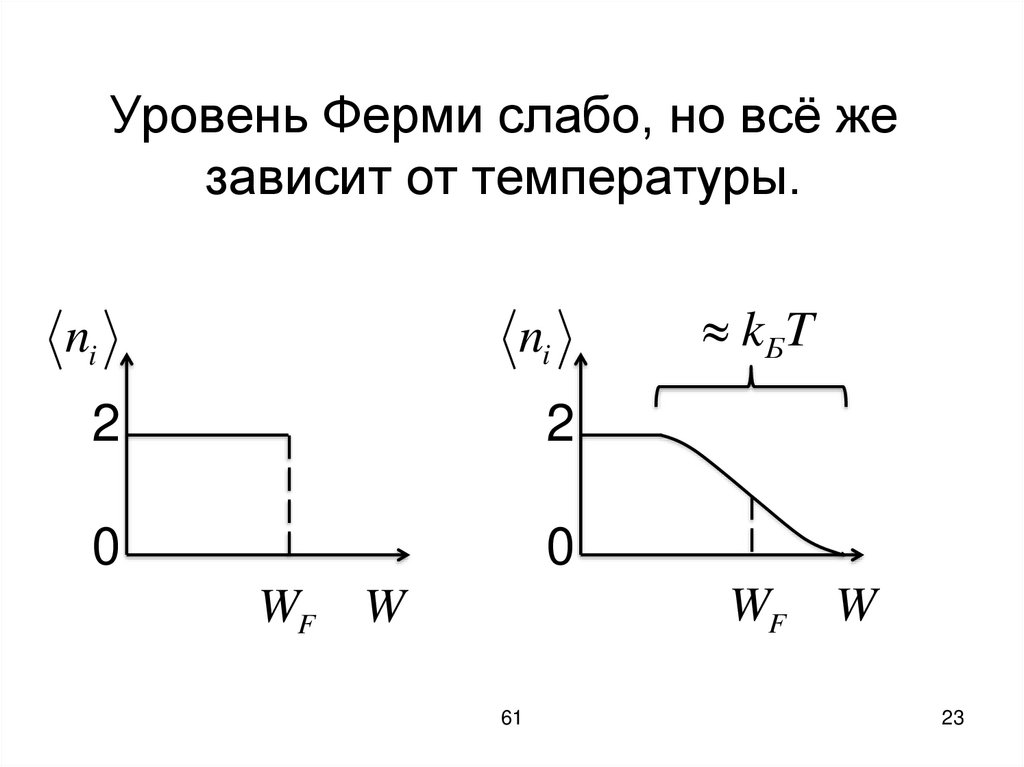
Уровень Ферми слабо, но всё жезависит от температуры.
ni
ni
2
2
0
0
k БT
WF W
WF W
61
23
24.
Средняя энергия тепловогодвижения, равная по порядку
величины kБT, составляет при
комнатной температуре 1/40 эВ.
Такая энергия может возбуждать
только электроны, находящиеся на
самых верхних уровнях,
примыкающих к уровню Ферми.
Остальная масса электронов
поглощать энергию не будет.
61
24
25.
6125
26.
24. Элементы зонной теориитвердых тел.
Металлы (проводники),
полупроводники и диэлектрики с
точки зрения зонной теории
твердых тел.
61
26
27.
Электрон – квантовая частица,обладающая волновыми
свойствами.
Согласно квантовой механике,
электрон в изолированном атоме
обладает определённым набором
энергетических уровней.
Для одинаковых атомов эти уровни
одинаковы.
61
27
28.
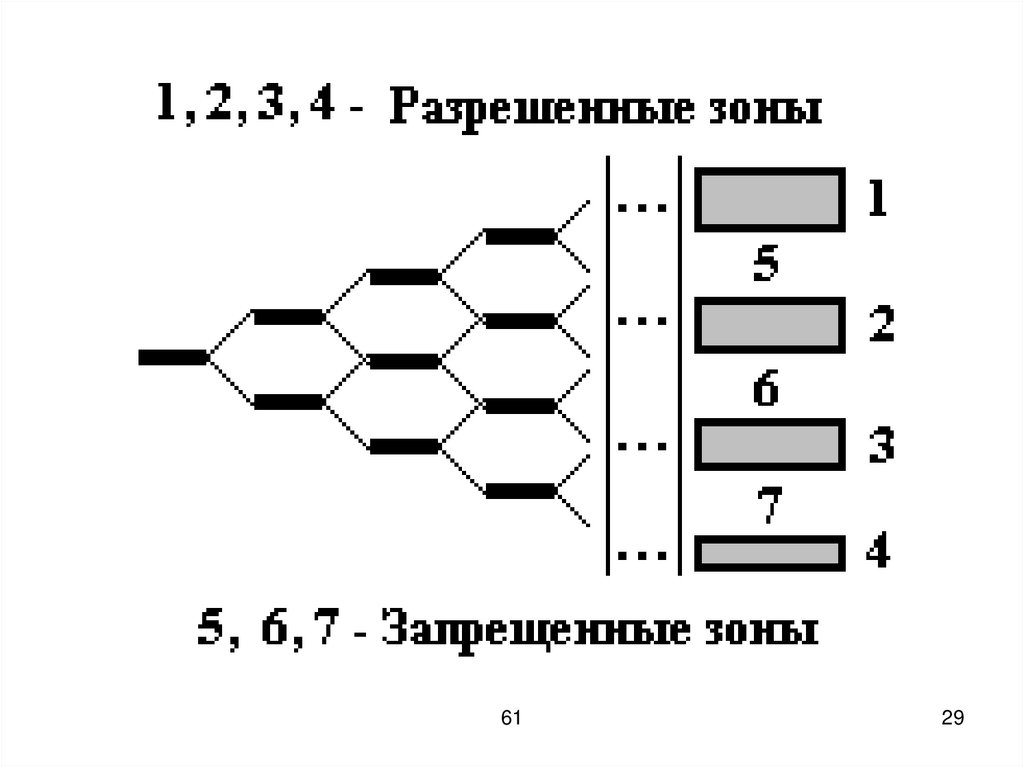
При сближении атомов(допустим N штук)
на месте одного, одинакового для
всех атомов, возникает N уровней,
очень близких. Такие уровни
образуют полосу или зону.
Уровни, заполненные в атоме
внешними электронами,
возмущаются сильнее.
61
28
29.
6129
30.
Расстояние между уровнями вразрешенной зоне кристалла очень
мало. Например, при ширине
разрешенной зоны в 1 эВ
(1эВ = 1,6 10 19 Дж) это расстояние
составляет примерно 10 22 эВ.
Но число уровней в разрешенных
зонах конечно, что оказывает
влияние на распределение
электронов по энергетическим
состояниям.
61
30
31.
6131
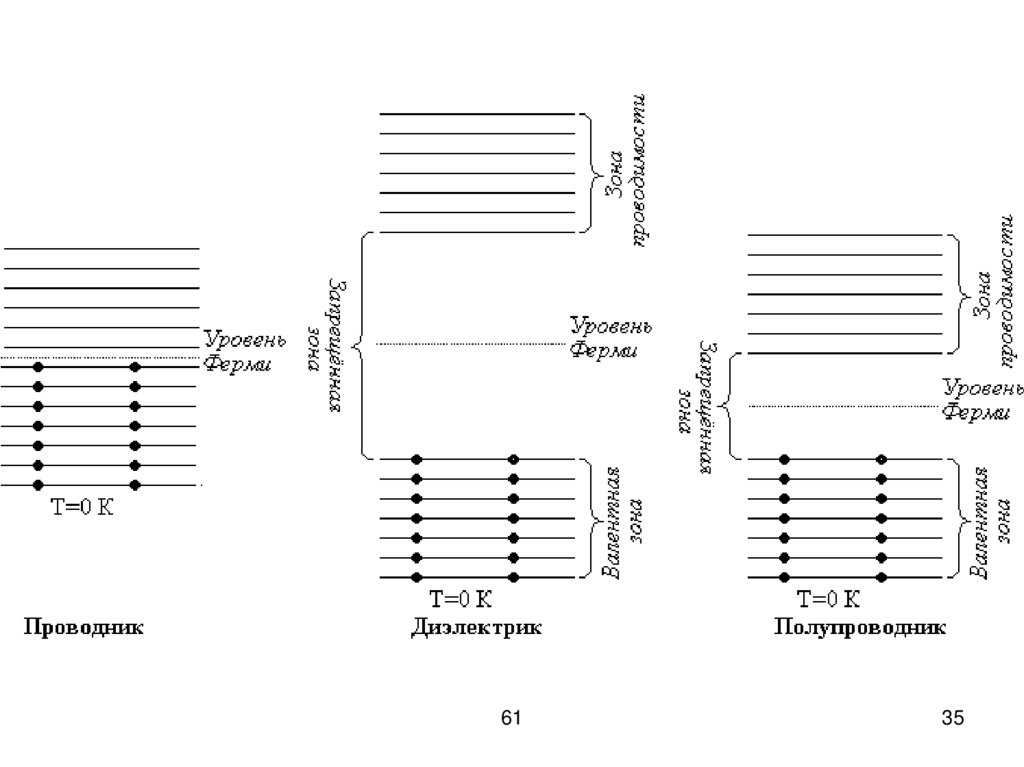
32.
Заполнение зон.Металлы – вещества с высокой
электро- и теплопроводностью,
хорошо отражают электромагнитные
волны, зависимость сопротивления
от температуры – ρ = ρ0 (1 + αt).
Диэлектрики (изоляторы) – вещества
с очень низкой
электропроводностью.
61
32
33.
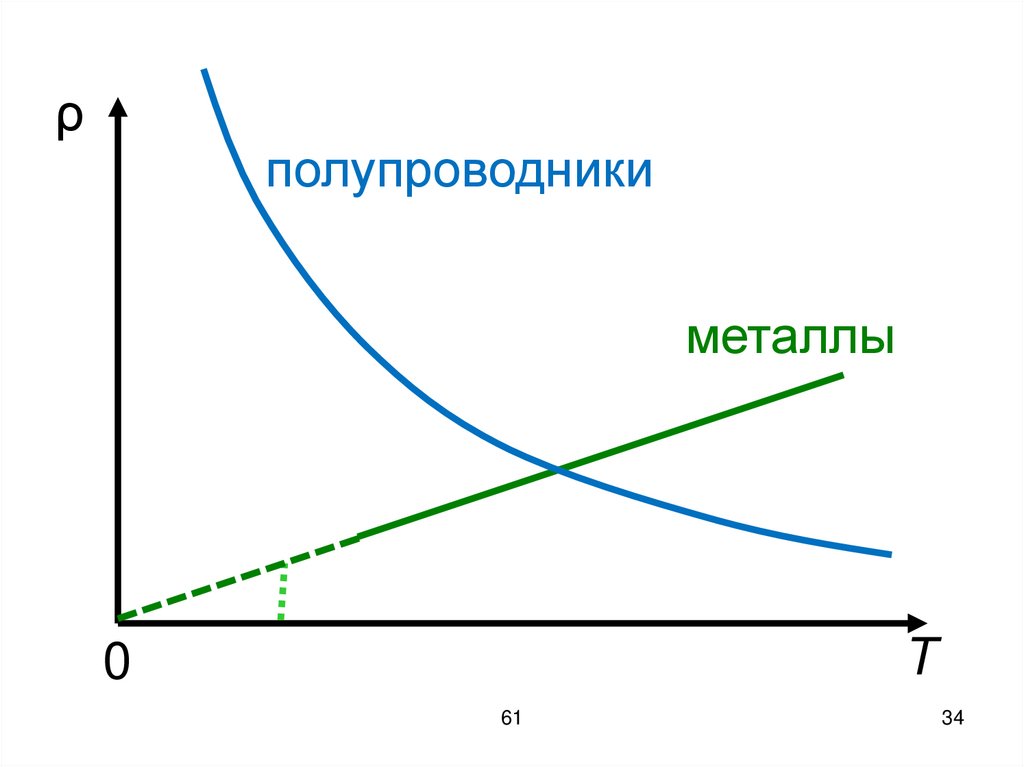
Полупроводники – широкий классвеществ, с промежуточным
значением сопротивления или
проводимости по сравнению с
металлами и диэлектриками.
Температурная зависимость
проводимости
(ΔW – размер запрещённой зоны)
σ σ 0e
W
2 kT
ρ ρ 0e
61
W
2 kT
33
34.
ρполупроводники
металлы
T
0
61
34
35.
6135
36.
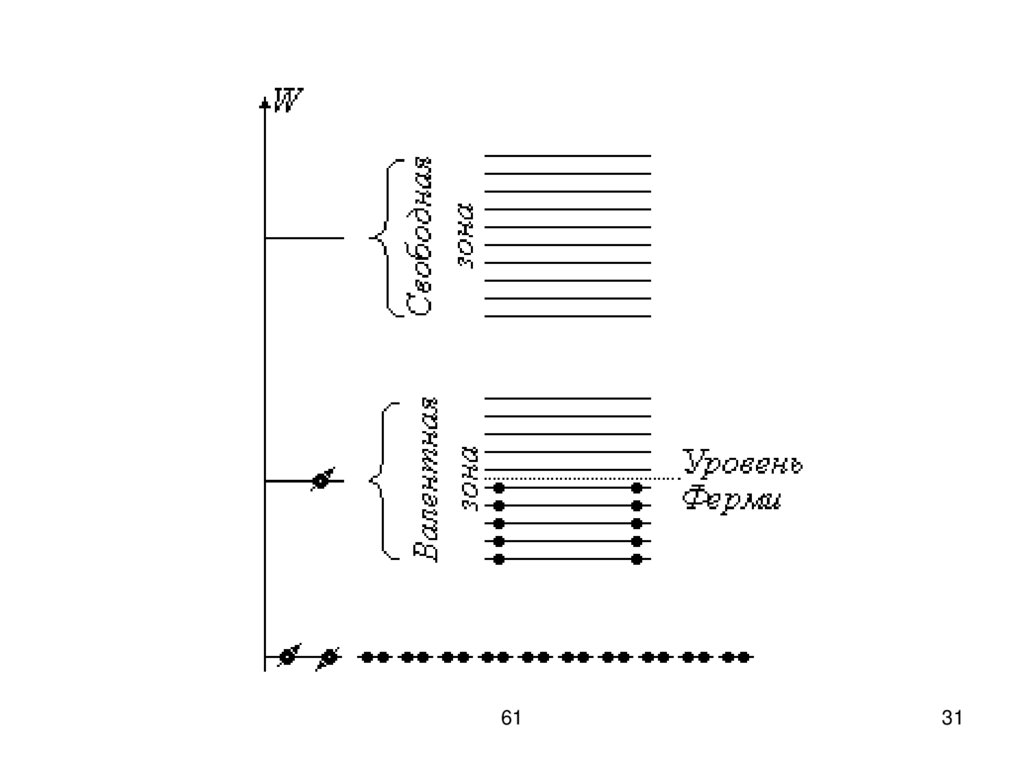
В металлах валентный уровеньзаполнен не полностью, поэтому для
перевода электрона на более
высокий уровень достаточно мало
энергии (10-23-10-22 эВ – расстояние
между соседними уровнями).
Энергии теплового движения
(~10-4 эВ) для этого достаточно.
61
36
37.
Достаточно даже дополнительнойэнергии со стороны электрического
поля
(может быть сообщена электронам
энергия
W 10 3 эВ при Е = 105 В/м –
обычные источники тока).
61
37
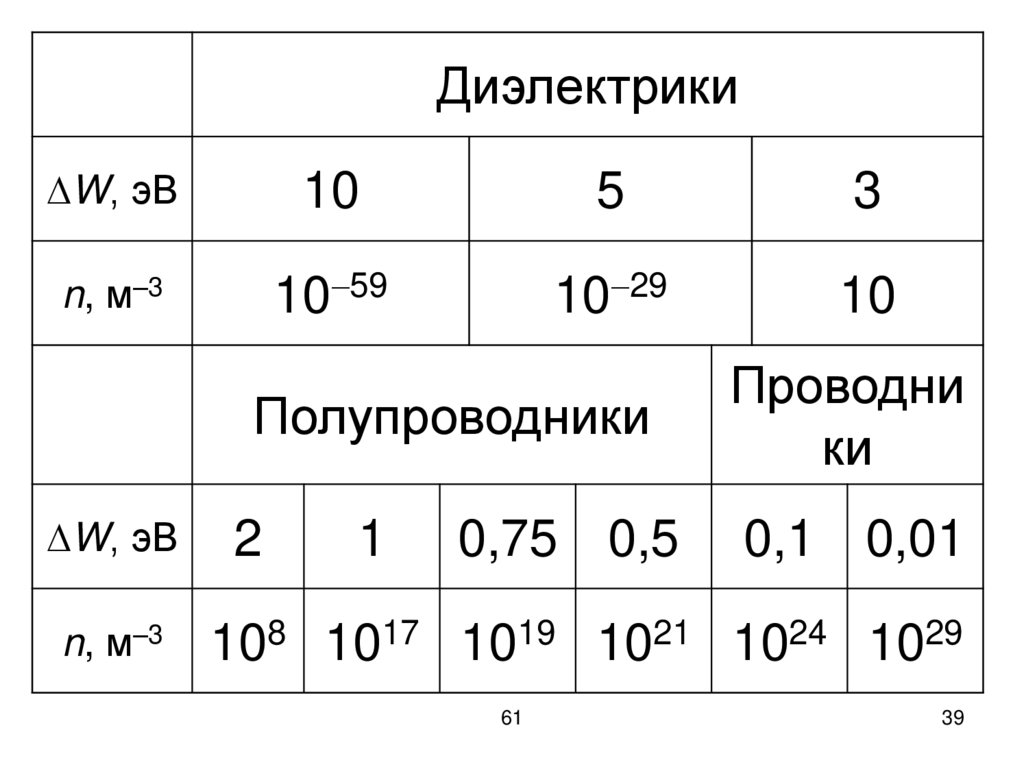
38.
В таблице приведены значенияширины запрещенной зоны
(энергии активации)
W и концентрации электронов n
в металлах, диэлектриках
и полупроводниках.
61
38
39.
ДиэлектрикиW, эВ
10
5
3
n, м–3
10 59
10 29
10
Полупроводники
Проводни
ки
W, эВ
2
0,1 0,01
n, м–3
108 1017 1019 1021 1024 1029
1
0,75 0,5
61
39
40.
6140
41.
25. Электросопротивление,его температурная зависимость.
Сверхпроводимость.
Свойства сверхпроводников.
Высокотемпературные
сверхпроводники.
61
41
42.
Зависимость сопротивления оттемпературы в металлах –
ρ = ρ0 (1 + αt).
Эта зависимость
экспериментальная, она плохо
согласуется с выводами
классической теории:
1
ne λ
σ
μne
ρ
2m
2
61
42
43.
но хорошо соответствует квантовойтеории, которая учитывает волновые
свойства электрона:
ne τ
σ
2m *
2
здесь n – концентрация электронов,
τ – время релаксации – время, за
которое скорость дрейфа электрона
уменьшается в «е» раз,
61
43
44.
m* – эффективная масса электронаm* 2
2
d ε dk
2
ε – энергия электрона,
k – волновой вектор электрона.
61
44
45.
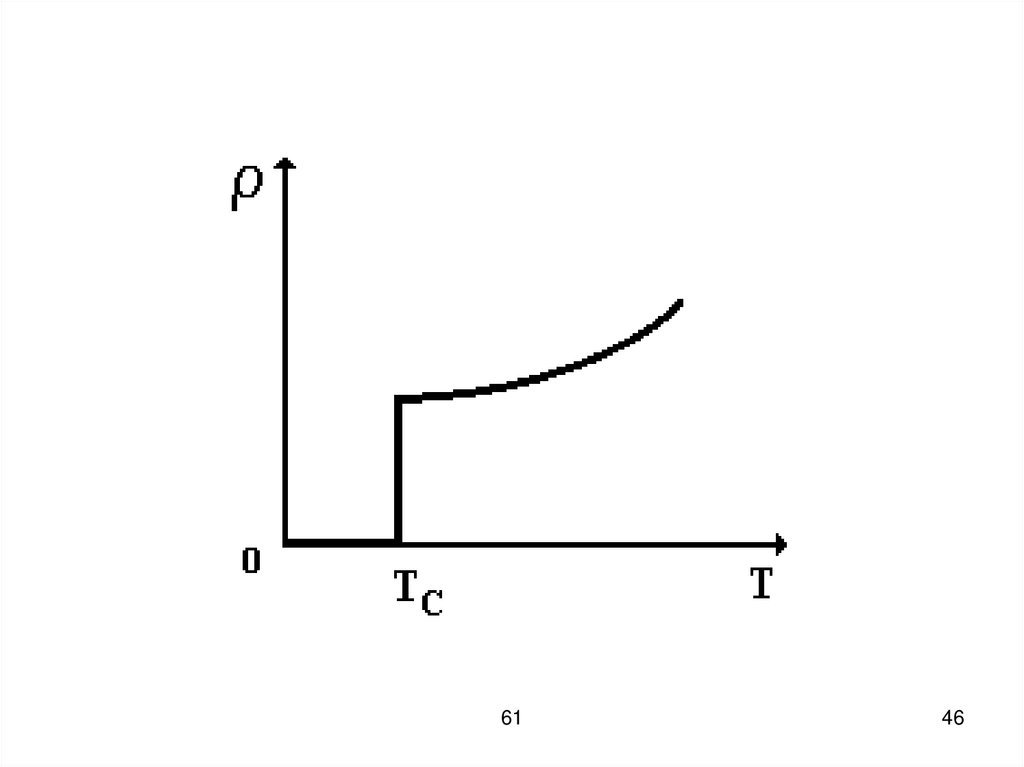
Вблизи абсолютного нуля возможнотак называемое сверхпроводящее
состояние. Сверхпроводимость
свойство многих веществ, в том
числе и проводников и многих
сплавов и др., состоящее в том, что
их электрическое сопротивление
скачком уменьшается до нуля при
охлаждении образцов ниже
критической температуры ТС,
характерной для данного материала.
61
45
46.
6146
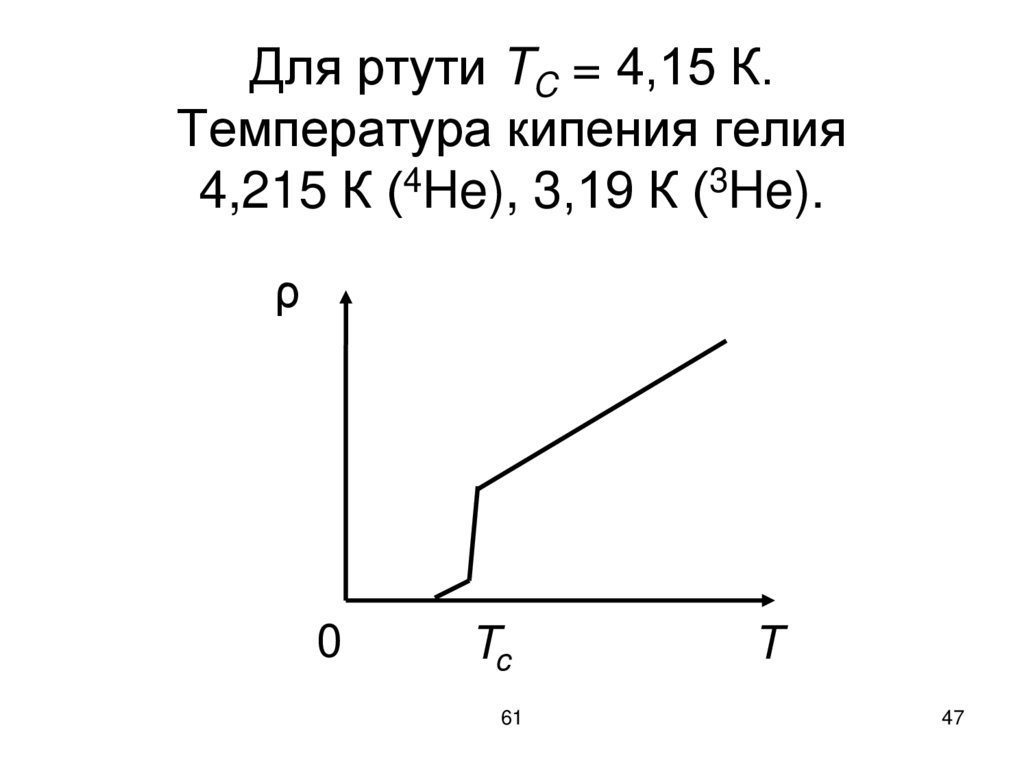
47.
Для ртути TC = 4,15 К.Температура кипения гелия
4,215 К (4He), 3,19 К (3He).
ρ
0
Tc
61
T
47
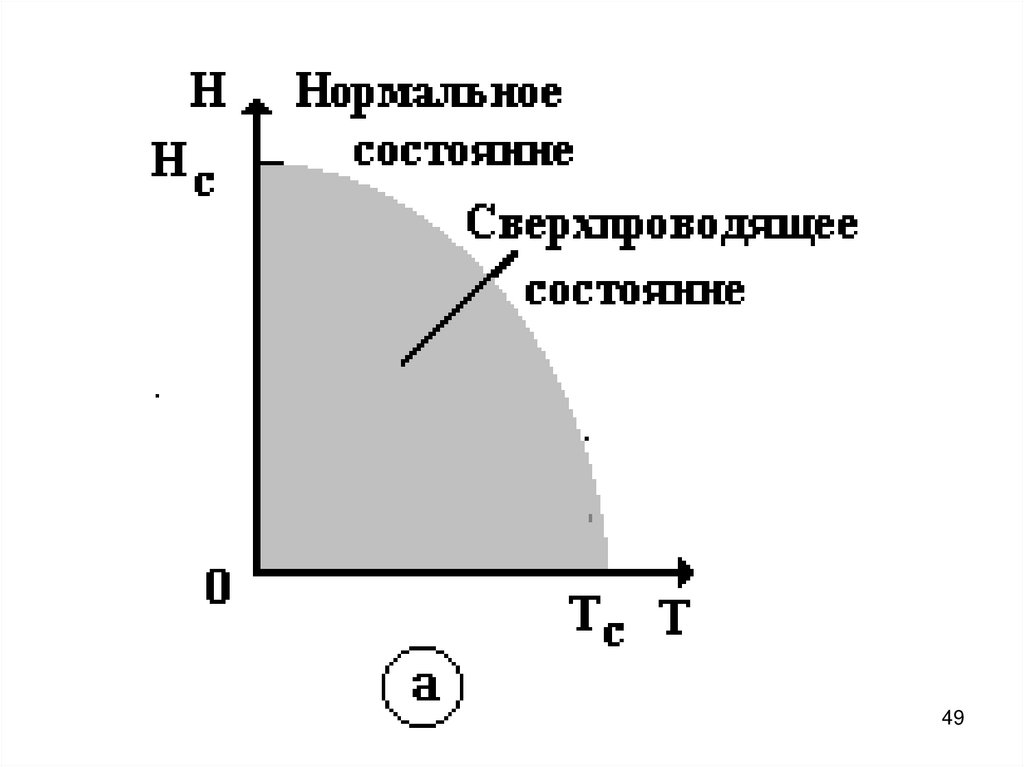
48.
Если при превышении некоторогозначения температуры
(или магнитной индукции
или силы тока)
сверхпроводящее состояние
разрушается, то это значение
называется критическим.
Критическое значение тем меньше,
чем больше два других параметра.
61
48
49.
6149
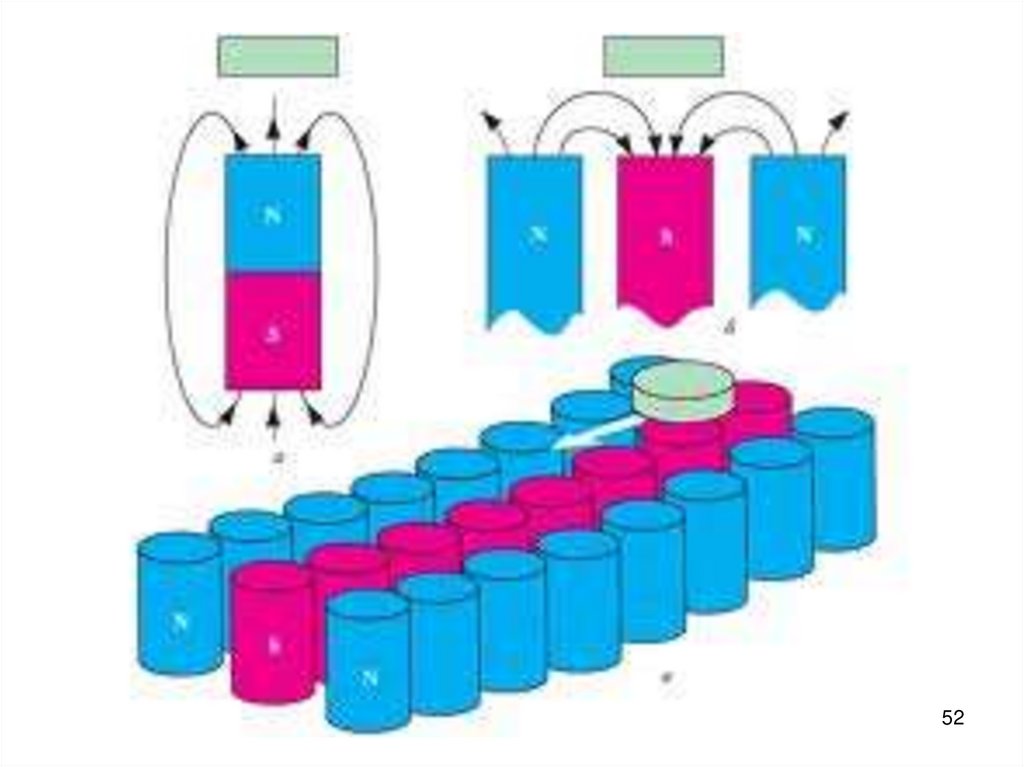
50.
Сверхпроводники – идеальныедиамагнетики, они полностью
выталкивают из себя магнитное поле
(μ = 0).
Эффект Мейснера – магнитное поле
в сверхпроводник не проникает,
поэтому возможно зависание
сверхпроводника в воздухе,
исключительно за счет внешнего
магнитного поля.
61
50
51.
6151
52.
6152
53.
Куперовское спаривание электронов:электроны проводимости, с
различными спинами могут
объединяться в так называемые
куперовские пары.
61
53
54.
Такие пары представляют бозон, абозоны могут накапливаться в
основном состоянии, из которого их
сравнительно трудно перевести в
возбуждённое состояние.
Такие пары существуют долго и
двигаются согласованно – это и есть
ток сверхпроводимости.
61
54
55.
Спин бозонов равен целому числу(0, ±1) и их распределение по
энергиям описывается формулой
Бозе-Эйнштейна:
1
ni
e
Wi WF
kT
61
1
55
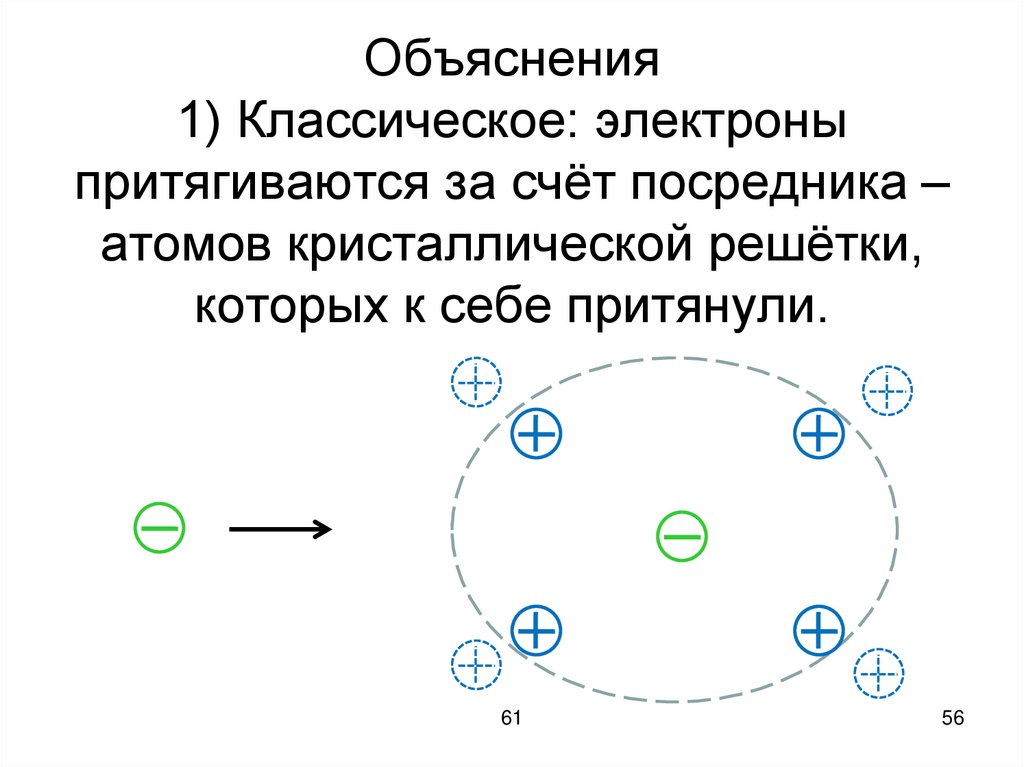
56.
Объяснения1) Классическое: электроны
притягиваются за счёт посредника –
атомов кристаллической решётки,
которых к себе притянули.
61
56
57.
2) Квантовое: электроныобмениваются фононами.
При низких температурах, у
сверхпроводников это притяжение
больше кулоновского отталкивания.
Расстояние между куперовскими
электронами примерно 10–4 см.
Фононы – квазичастицы,
передающие колебания в твёрдых
телах (фонон – квант колебаний).
61
57
58.
Чтобы разрушить такую связьнеобходимо паре сообщить энергию
3,2kБTкрит 1 T Tкрит
Это размеры щели, запрещённой
зоны, которая появляется в
энергетическом спектре электрона в
области уровня Ферми, когда он
образует пару.
61
58
59.
Квантование потокаИз теории сверхпроводимости
следует, что магнитный поток Φ,
связанный со сверхпроводящим
кольцом, по которому циркулирует
ток, должен быть равен
2π
n 0 n
, n 1,2,3
q
Φ0 – квант магнитного потока,
q – заряд носителя тока.
61
59
60.
Высокотемпературнаясверхпроводимость (ВТСП):
Обычная сверхпроводимость
Tкрит.макс. = 23,2 К (Nb3Ge).
ВТСП открыта в 1986 г (Беднорц и
Мюллер), основа оксид меди, по сути
керамика, (то есть проволоку не
вытянешь).
61
60
61.
HgBa2CaCu2O6 T = 125 KTl2B2CaCu2O8
T = 110 K
Bi2Sr2CaCu2O8 T = 95 K
YBa2Cu3O7-x
T = 90 K
температура жидкого азота
77 К
61
61
62.
Эффект ДжозефсонаПротекание сверхпроводящего тока
через тонкий слой диэлектрика,
разделяющий два сверхпроводника
– туннельный переход.
1-го рода: стационарный, I < Iк, ΔU=0.
2-го рода: нестационарный, I > Iк,
ΔU ≠ 0, идёт излучение
электромагнитных волн с частотой
ω = 2eU/ħ, через контакт течёт
переменный ток.
61
62
63.
Куперовска пара электронов припрохождении контакта получает
энергию 2eU, возвращаясь в
исходное состояние, пара излучает
эту энергию на частоте
2eU .
ω
61
63
64.
6164




















































 physics
physics








