Построение графиков функций. Решение уравнений и неравенств

1.

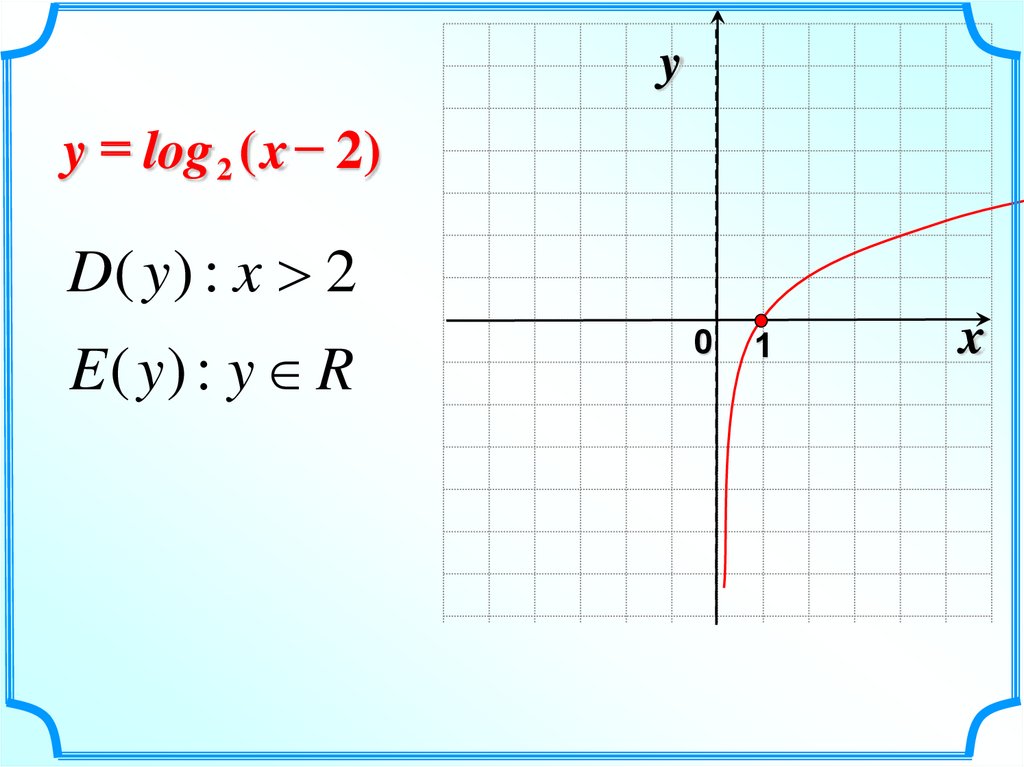
y
y = log 2 ( x – 2)
D( y ) : x 2
E ( y) : y R
0
1
x

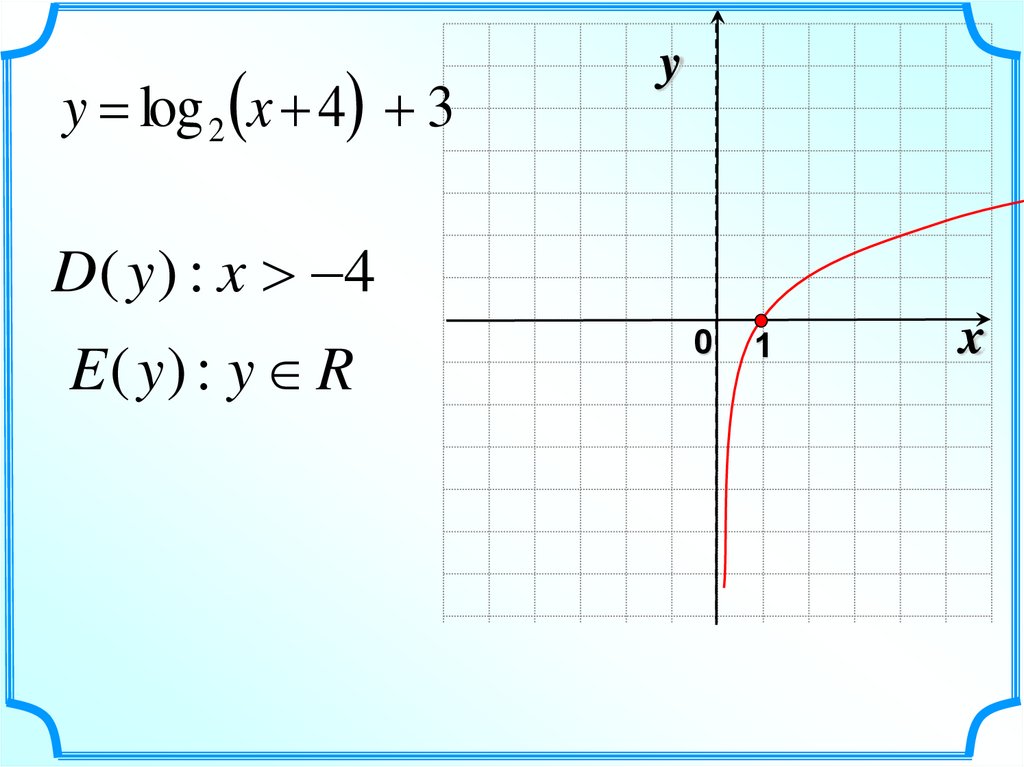
2.

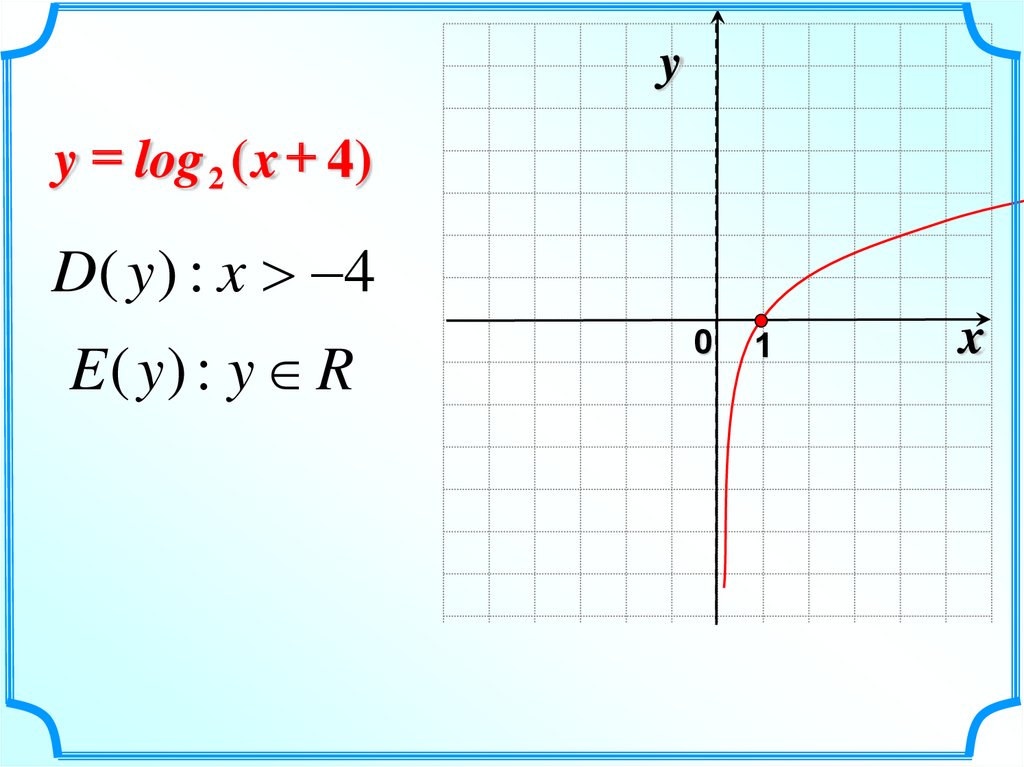
y
y = log 2 ( x + 4)
D( y ) : x 4
E ( y) : y R
0
1
x

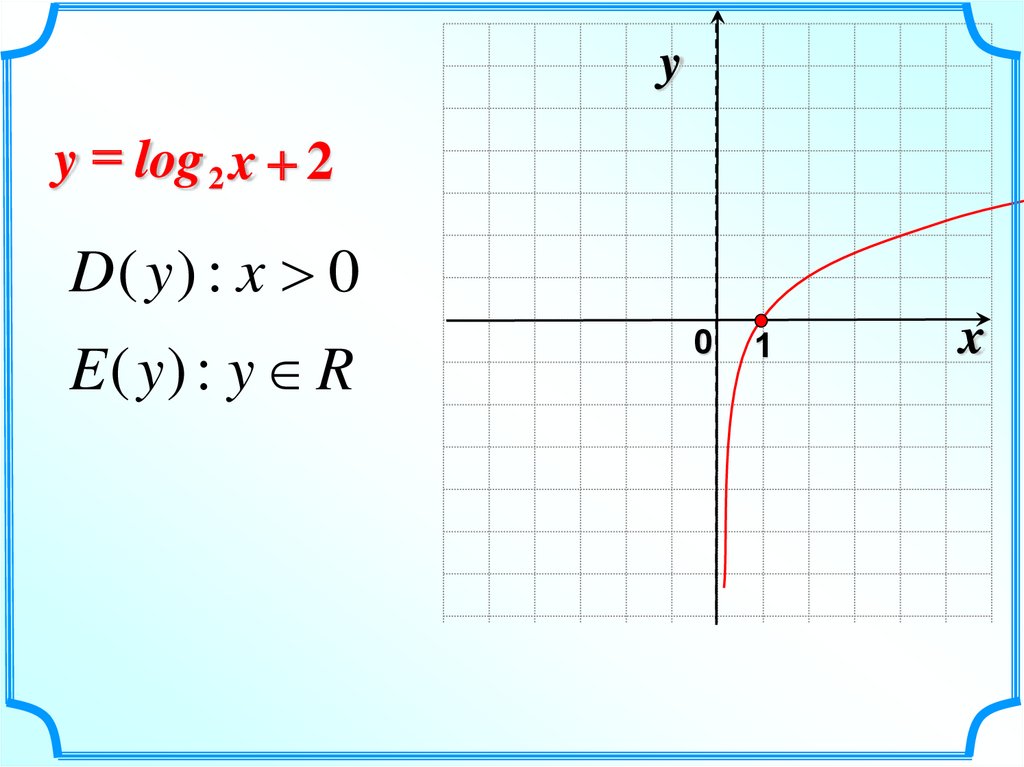
3.

y
y = log 2 x + 2
D( y ) : x 0
E ( y) : y R
0
1
x

4.

y = log 2 x + 4 + 3
y
D( y ) : x 4
E ( y) : y R
0
1
x

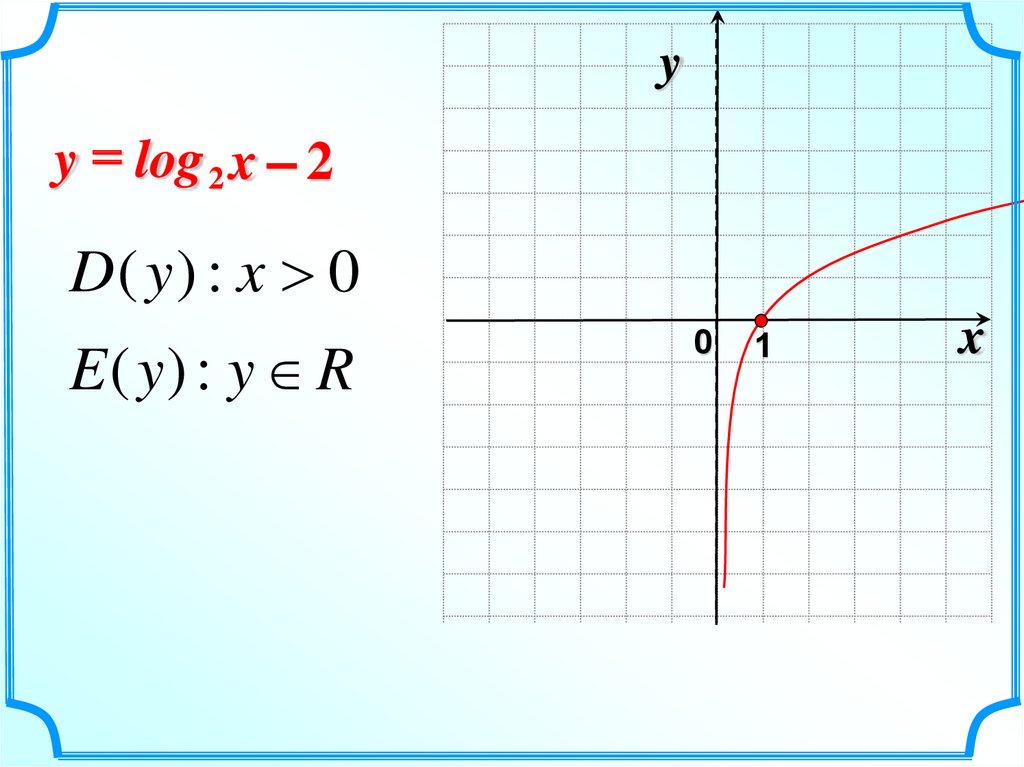
5.

y
y = log 2 x – 2
D( y ) : x 0
E ( y) : y R
0
1
x

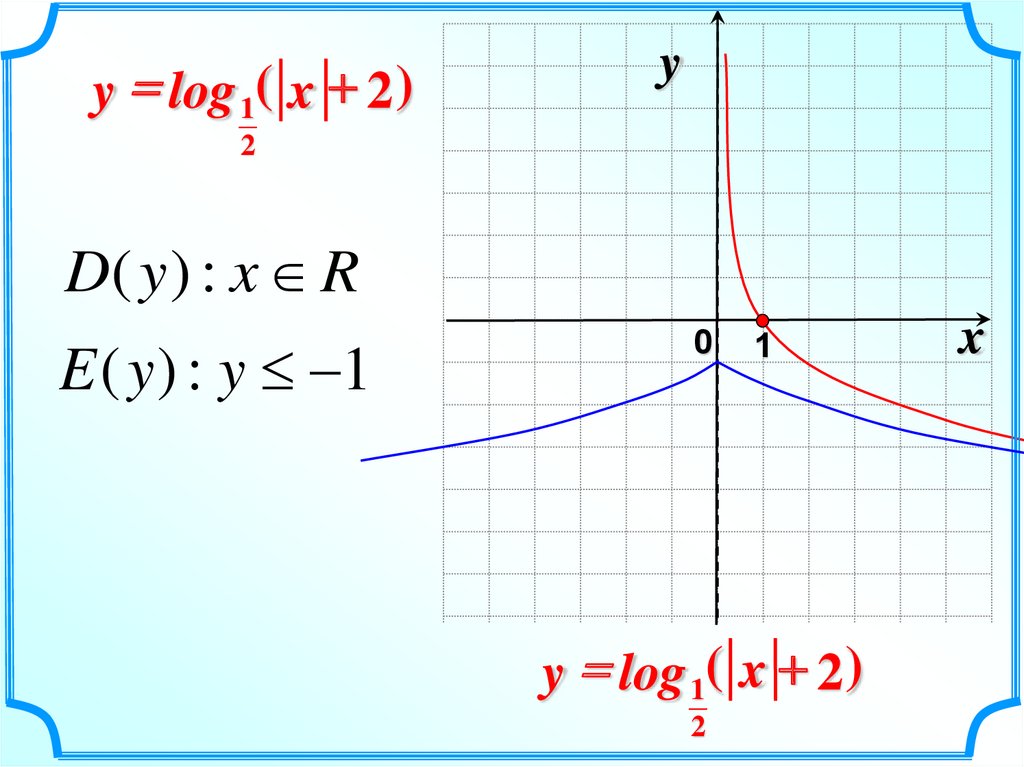
6.

y = log 1( x + 2 )
y
2
D( y ) : x R
E ( y ) : y 1
0
1
y = log 1( x + 2 )
2
x

7.

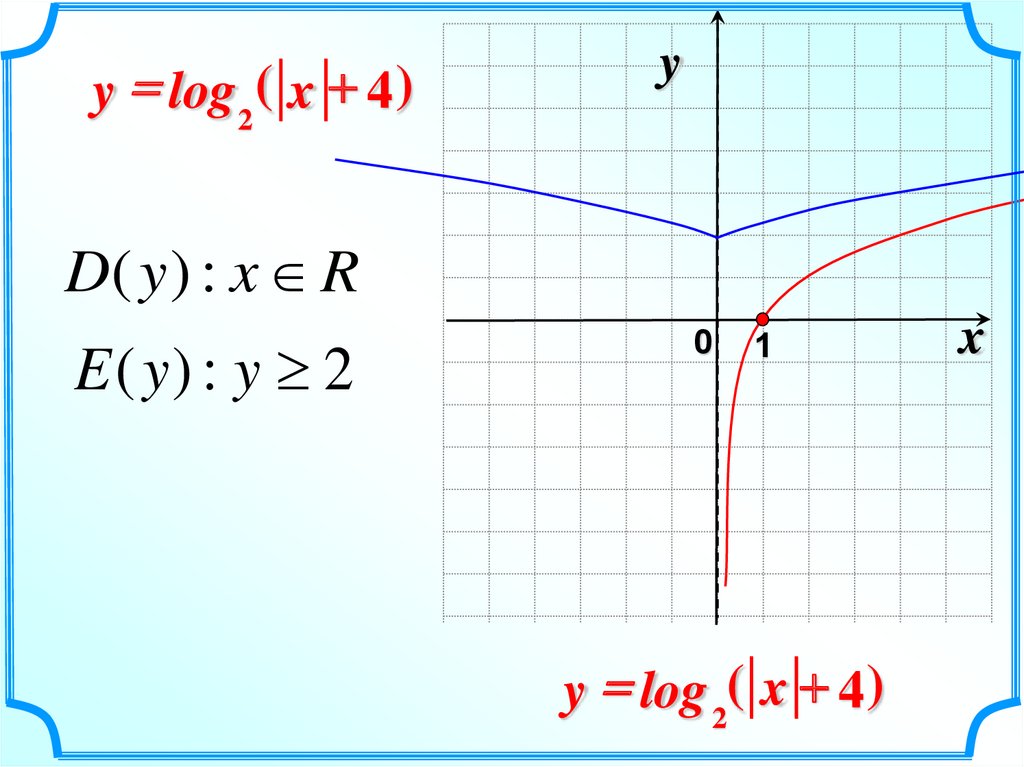
y = log 2 ( x + 4 )
y
D( y ) : x R
E ( y) : y 2
0
1
y = log 2( x + 4 )
x

8.

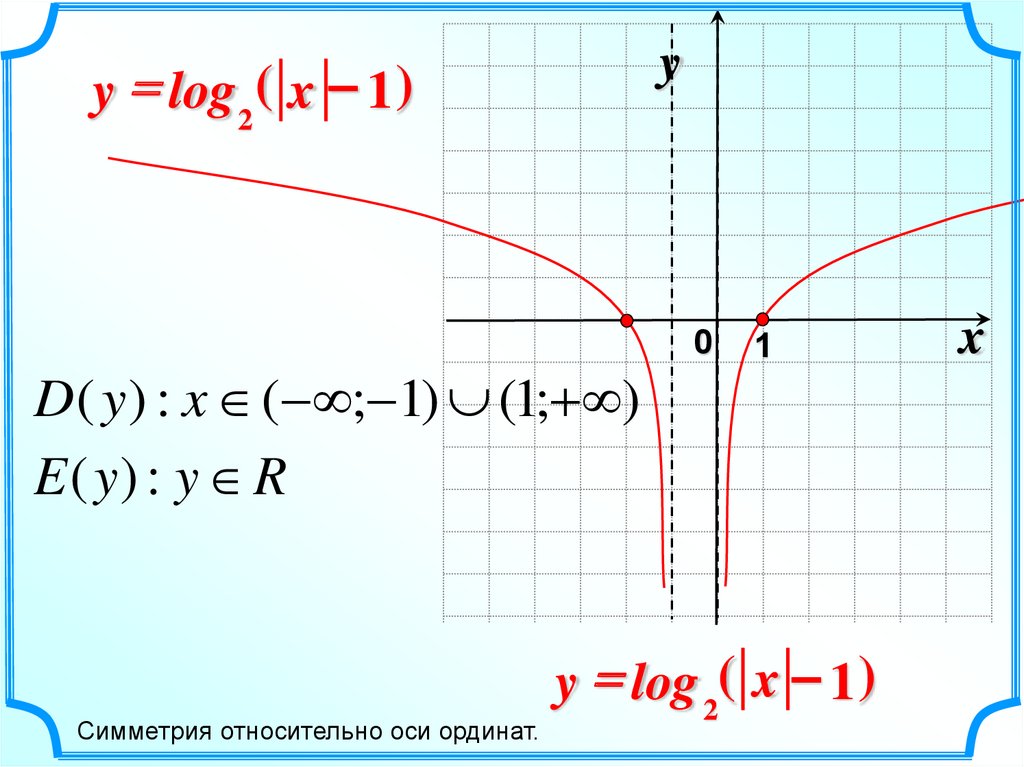
y
y = log 2 ( x – 1 )
0
D( y ) : x ( ; 1) (1;+ )
E ( y) : y R
Симметрия относительно оси ординат.
1
y = log 2( x – 1 )
x

9.

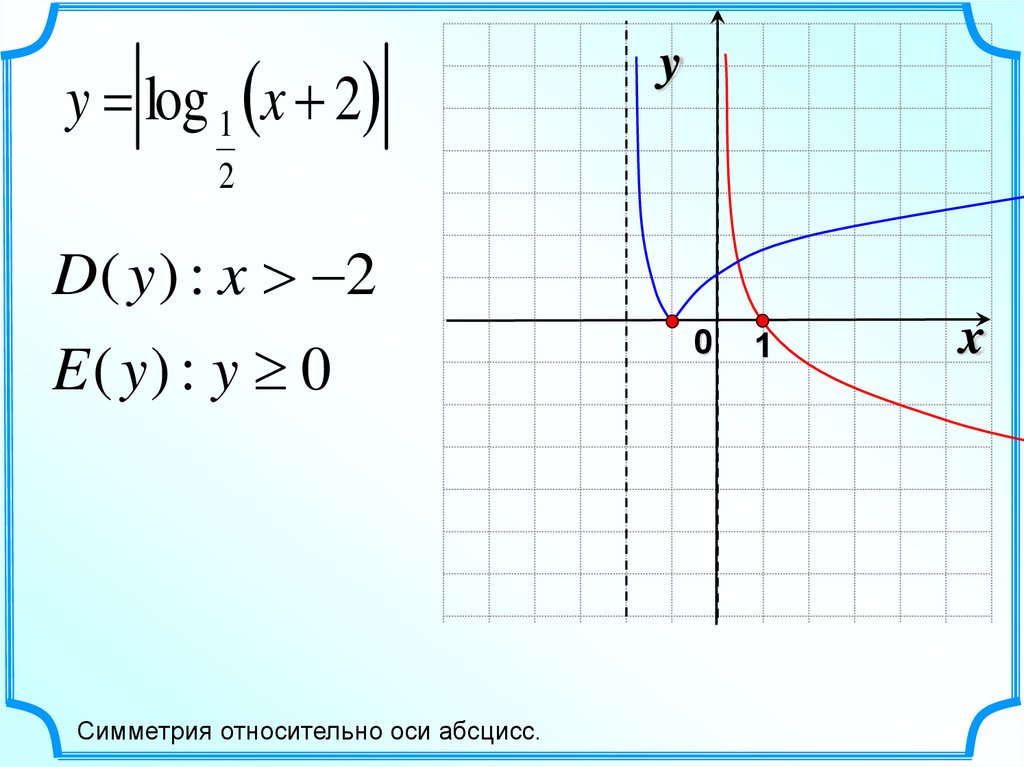
y = log 1 x + 2
y
2
D( y ) : x 2
E ( y) : y 0
Симметрия относительно оси абсцисс.
0
1
x

10.

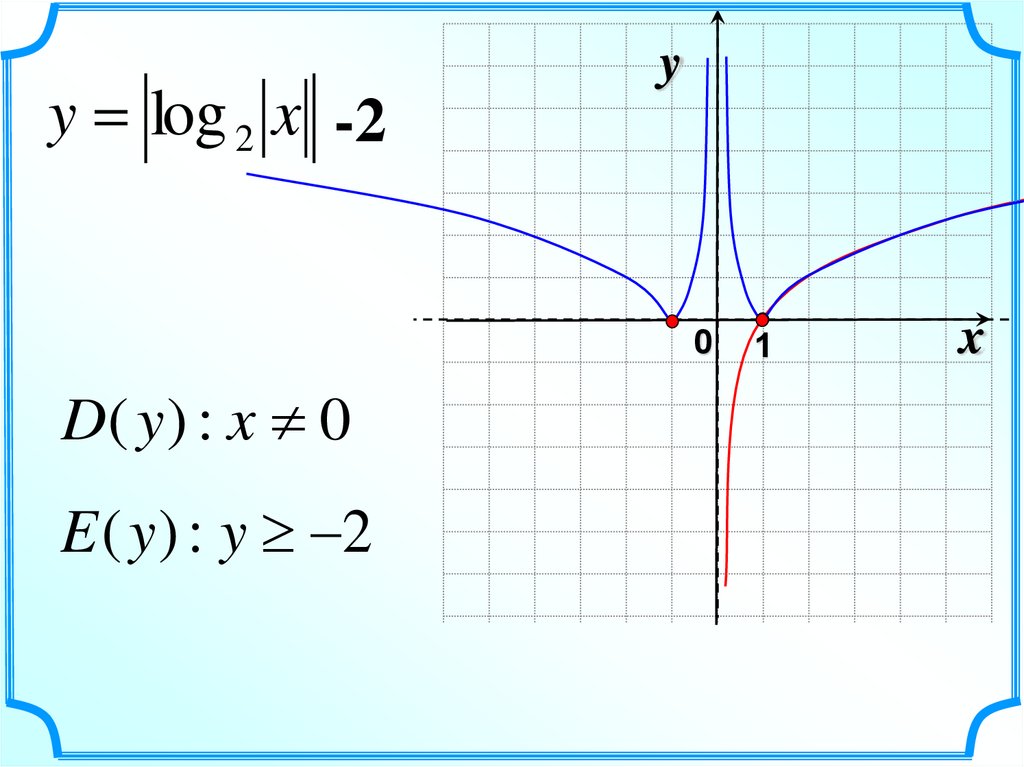
y = log 2 x -2
y
0
D( y ) : x 0
E ( y ) : y 2
1
x

11.

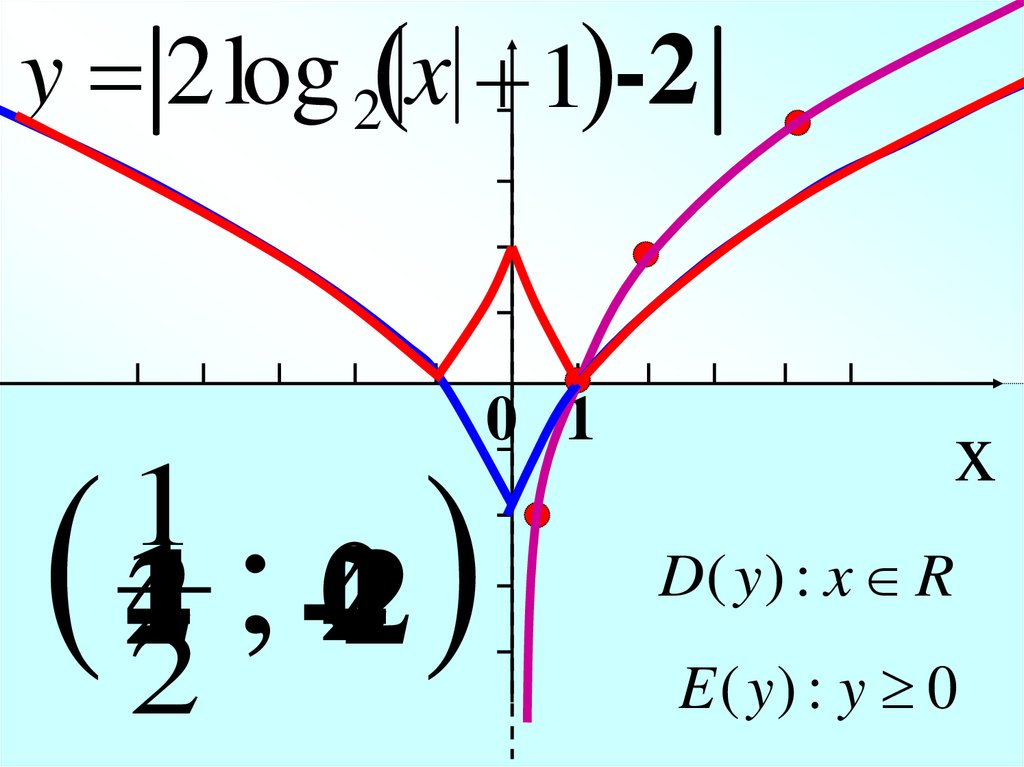
y = 2 log 2 x + 1 -2
1
1
02
2 ; -2
4
4
2
0 1
x
D( y ) : x R
E ( y) : y 0

12.

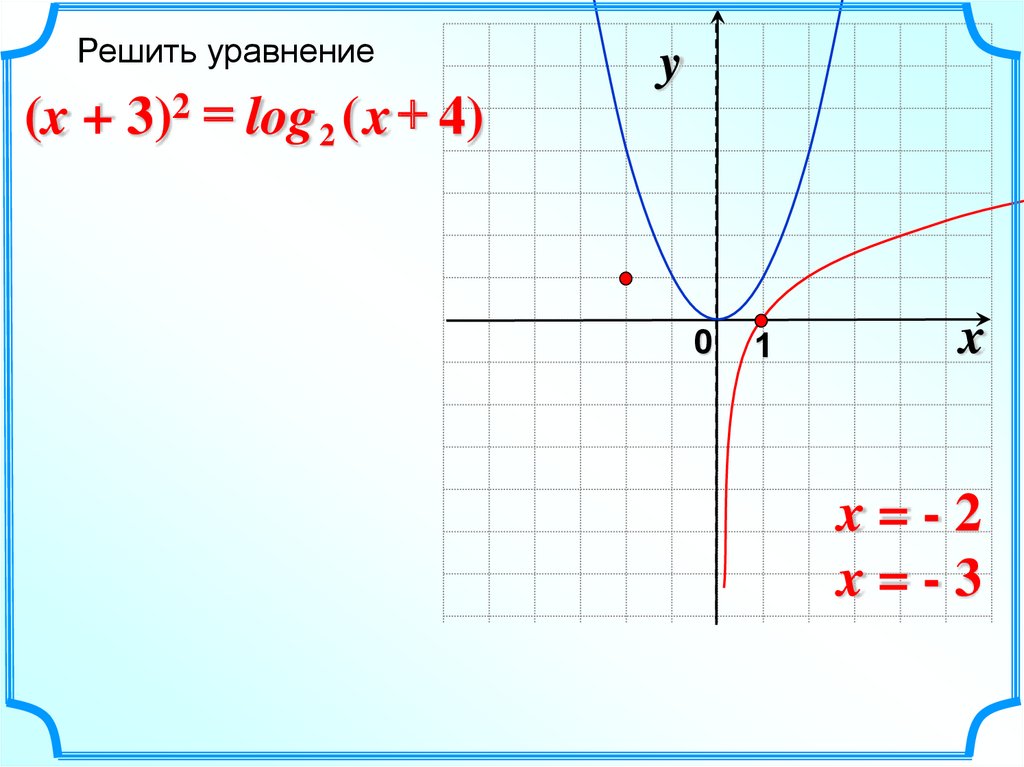
Решить уравнение
(x + 3)2 = log 2 ( x + 4)
y
0
1
x
x=-2
x=-3

13.

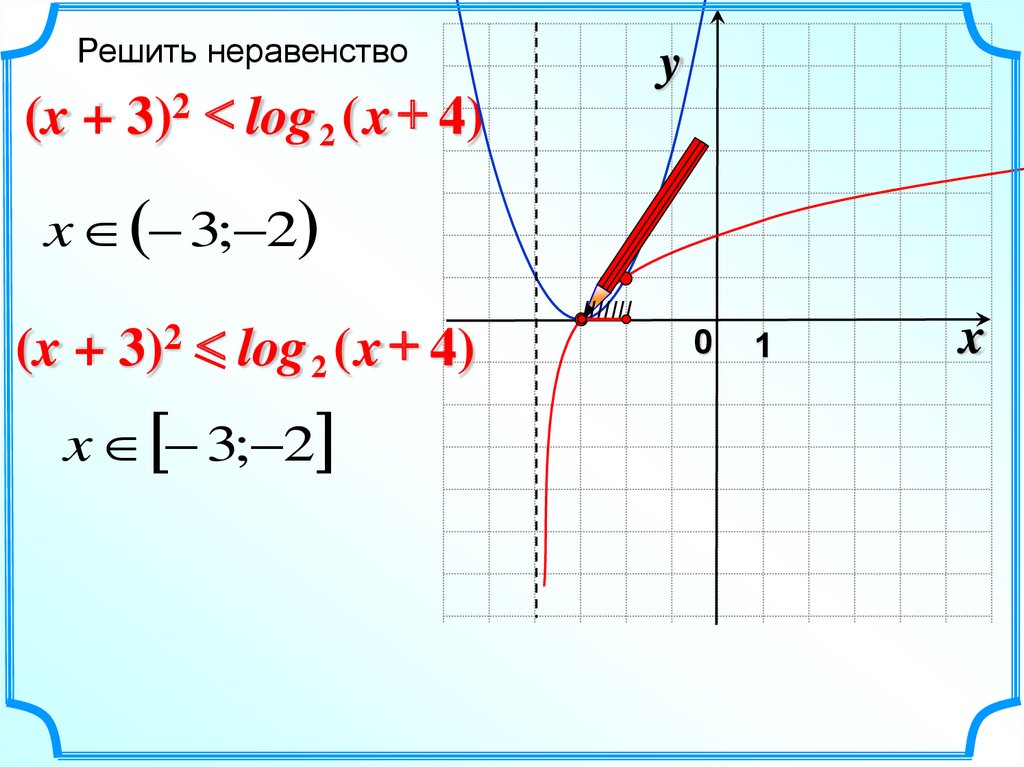
Решить неравенство
y
(x + 3)2 < log 2 ( x + 4)
x 3; 2
(x + 3)2 < log 2 ( x + 4)
x 3; 2
IIIIIII
0
1
x

14.

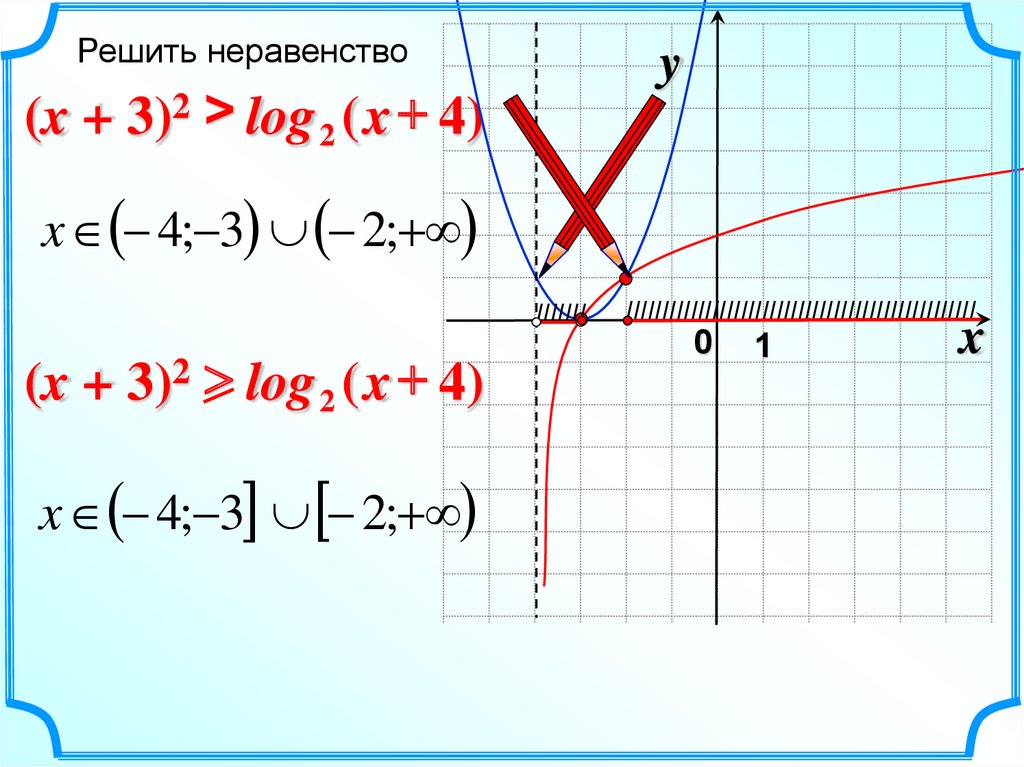
Решить неравенство
y
(x + 3)2 > log 2 ( x + 4)
x 4; 3 2;+
IIIIIII
(x + 3)2 log 2 ( x + 4)
x 4; 3 2;+
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
1
x

15.

Решить уравнение
y
log2(x + 2) – 1 = x + 2 2
0
x
1
x=-1

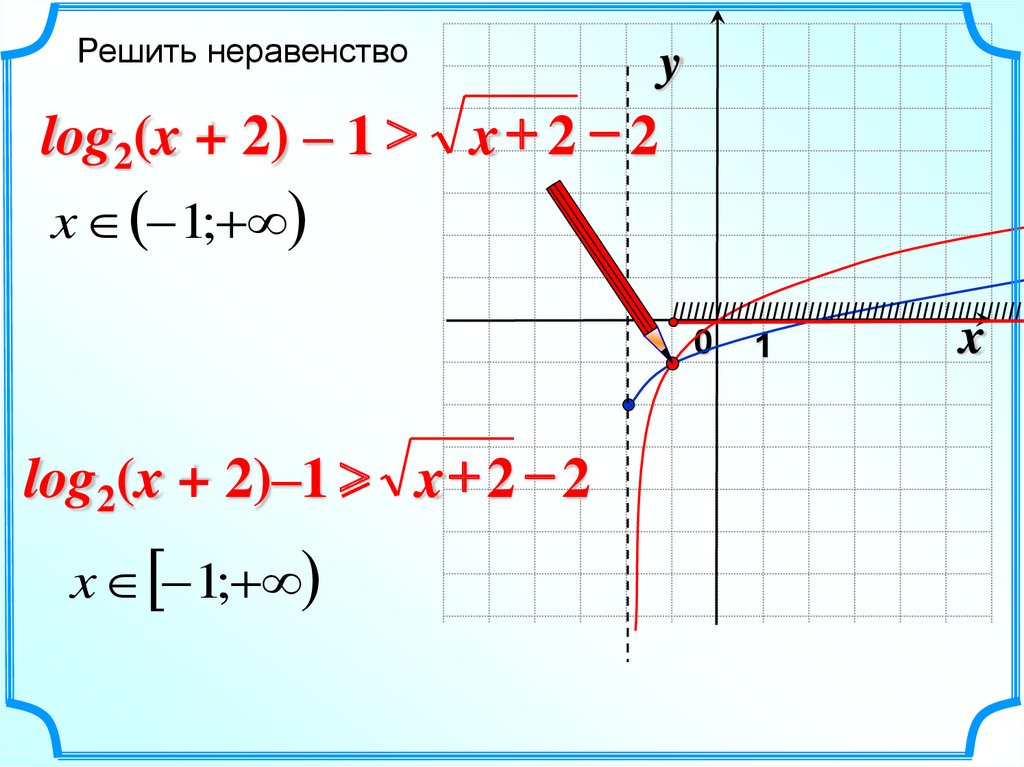
16.

Решить неравенство
y
log2(x + 2) – 1 x + 2 2
x 1;+
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
log2(x + 2)–1 x + 2 2
x 1;+
1
x

17.

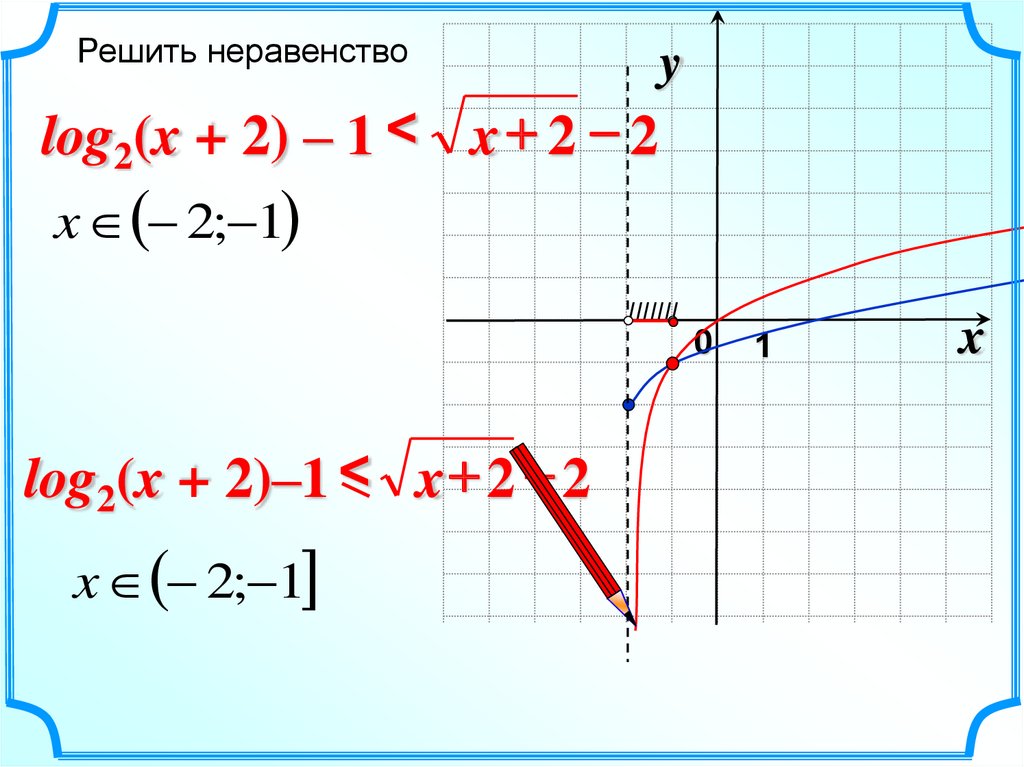
Решить неравенство
y
log2(x + 2) – 1 < x + 2 2
x 2; 1
IIIIIII
0
log2(x + 2)–1 < x + 2 2
x 2; 1
1
x