Similar presentations:
Системы тригонометрических уравнений
1.
2.
1. Системы уравнений, в которых одно уравнение –алгебраическое, а другое – сумма или разность
тригонометрических функций.
Примеры:
х у а,
а)
1
sin x sin y 2 ;
5
x y 6 ,
в )
2
cos x cos 2 y 1 ;
4
2
х у ,
3
б )
tgx tgy 2 3;
x
y
3 ,
г )
ctgx ctgy 3.
3.
2. Системы уравнений, в которых одно уравнение –алгебраическое, а другое – произведение
тригонометрических функций.
Примеры:
х у а,
а)
sin x sin y b;
x y a,
б )
sin x cos y b;
x y a,
в)
cos x cos y b;
7
x y 12 ,
г )
tgx ctgy 3 ;
3
x y ,
д)
1
ctgx ctgy 3 .
4.
3. Системыуравнений, в которых
одно уравнение – алгебраическое,
а другое – отношение тригонометрических функций.
x y a,
а) sin x
b
;
sin y
x y a,
г ) cos x
b
;
cos y
Примеры:
x y a,
x y a,
в ) ctgx
б ) tgx
b
;
b
;
ctgy
tgy
x y a,
д) cos x
b
;
sin y
5.
4. Системы уравнений, содержащих толькотригонометрические функции.
Примеры:
1
sin
x
cos
y
,
4
а)
sin 2 x cos 2 y 1 ;
2
1
sin
x
sin
y
,
4
в )
3
cos x cos y ;
4
y
x
tg tg 2,
б ) 2
2
ctgx ctgy 1,8;
3tgx tg y,
г )
cos x sin 2 y.
3
6.
1. Решить систему уравненийx y 3 ,
cos x cos y 3 .
2
Решение.
x y 3 , (1)
cos x cos y 3 ; (2).
2
x y
x y 3
Из (2) следует:
2 cos
cos
.
2
2
2
x y
3
2 cos
cos ,
Из (1) следует:
2
6 2
x y
3
x y
3
x y 3 3
.
, cos
2 cos
, cos
2
2
2
2
2
2
2 3
7.
x y3
cos
.
2
2
x y
3
arccos
2 n, n ,
2
2
x y
2 n, n ,
2
6
x y
3
4 n, n .
Запишем систему:
x y 3 4 n, n ,
x y ;
3
8.
Запишем систему:x y 3 4 n, n ,
x y ;
3
Если сложить и вычесть уравнения системы, то получим систему,
равносильную исходной.
2
x
4
n
,
n
,
3 3
2 y 4 n, n ;
3 3
9.
2 x 3 3 4 n, n ,2 y 4 n, n ;
3 3
x
2
n
,
6 6
y 2 n, n .
6 6
Ответ: x 2 n , y 2 n , n .
6
6
6
6
10.
x y 6 ,2. Решить систему уравнений
cos x sin y 1 .
4
Решение.
x y 6 , (1)
cos x sin y 1 (2);
4
Из (2) следует:
1
1
(sin( x y ) sin( y х)) ,
2
4
1
(sin( x y ) sin( y х)) .
2
Из (1) следует:
1
sin( x y ) sin ,
6 2
sin( x y ) 1,
x y
2
2 n, n
11.
Запишем систему уравнений:x y 2 2 n, n ,
x y ;
6
2 x 2 6 2 n,
2 y 2 n, n ;
2 6
x 3 n,
y n, n .
6
Ответ:
x
3
Складывая и вычитая
уравнения системы,
получим систему,
равносильную исходной:
2
2 x 3 2 n,
2 y 2 n, n ;
3
(3n 1), y
6
(6n 1), n
12.
x y 6 ,3. Решить систему уравнений
sin x 2.
cos y
x y 6 ,
sin x
2.
cos y
Решение.
y x 6 ,
sin x 2 cos( x );
6
Решим второе уравнение системы:
sin x 2 cos( x ), (1).
6
Правую часть уравнения (1) распишем по формуле косинуса разности:
sin x 2 cos x cos
6
2 sin x sin
sin x 3 cos x sin x,
6
,
откуда cosx = 0,
x
2
n, n .
13.
xn
,
n
,
2
y x ;
6
x 2 n,
y n , n ;
2
6
x 2 n,
y n, n .
3
Ответ:
x
2
n, n , y
3
n, n .
14.
4. Решить систему уравненийsin x cos y
cos x sin y
3
,
4
3
.
4
sin x cos y
cos x sin y
Решение.
3
,
4
3
.
4
Если сложить и вычесть уравнения системы, то получим систему
равносильную исходной. Итак:
3
,
sin x cos y cos x sin y
2
sin x cos y cos x sin y 0.
15.
Применим формулы сложения:3
,
sin( x y )
2
sin( x y ) 0;
n
x y 1 n, n ,
3
x y k , k .
При решении независимых простейших уравнений необходимо писать
разные целочисленные параметры, иначе будет потеряно множество
корней.
Сложим и вычтем уравнения системы(1):
n
2 x 1 3 n k , n, k ,
2 y 1 n n k , n, k ;
3
16.
1n
x 1 6 2 (n k ) , n, k ,
y 1 n 1 (n k ) , n, k .
6 2
Ответ:
1
x 1 (n k ) ,
6 2
1
n
y 1 (n k ) , n, k
6 2
n






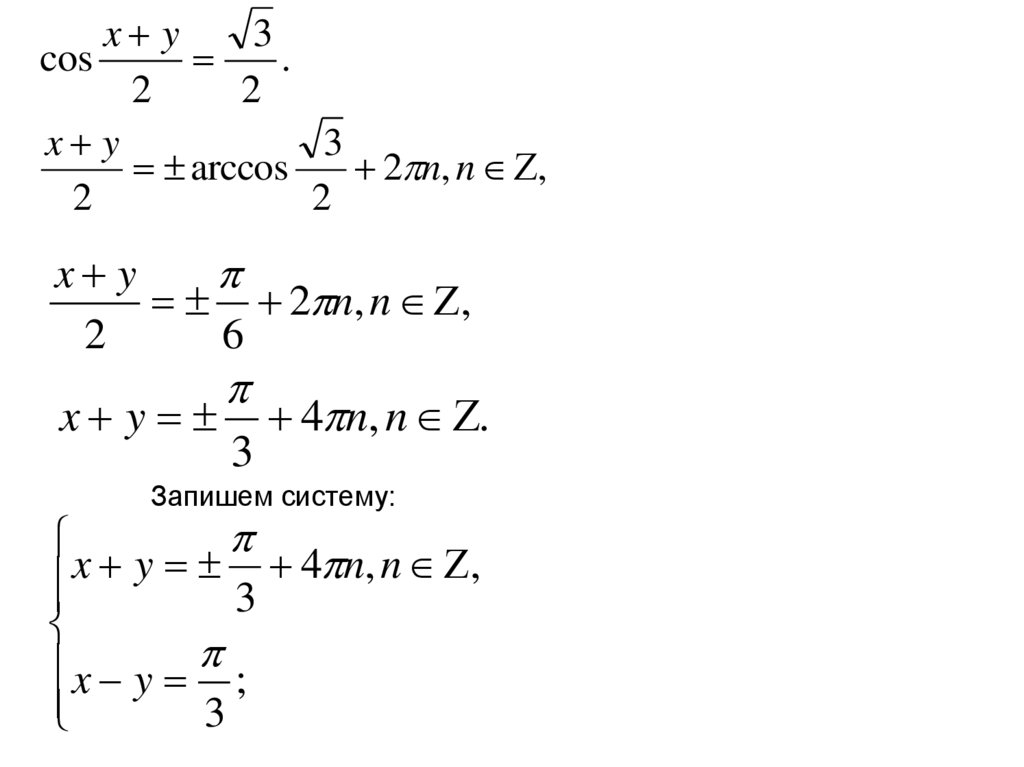

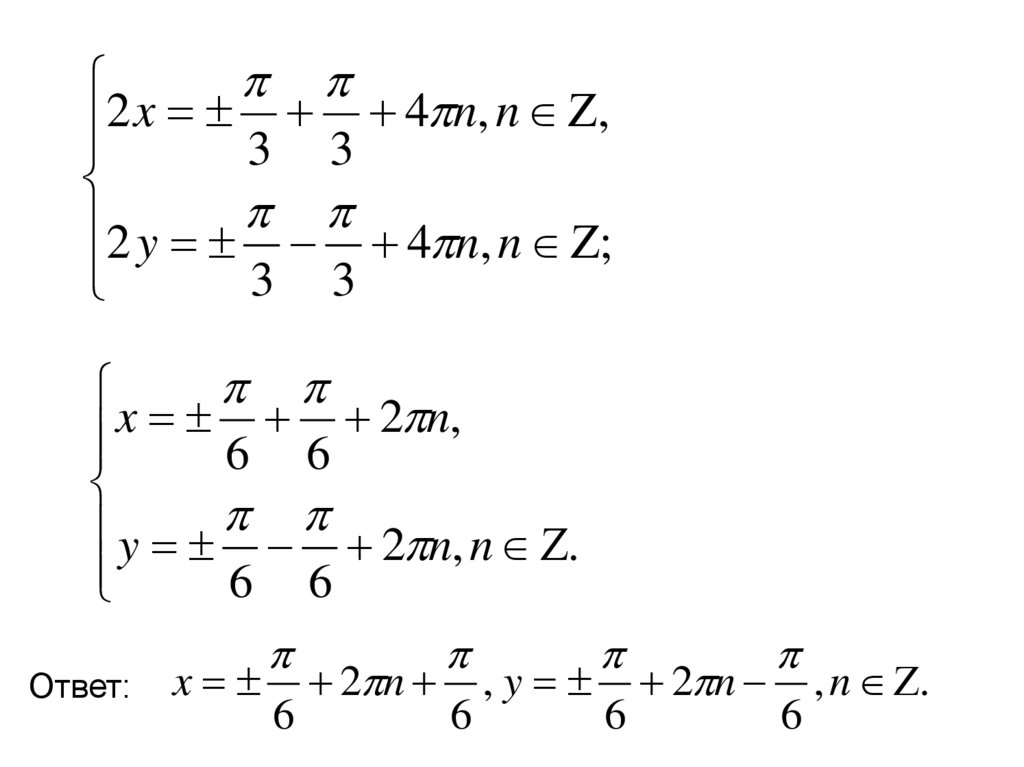



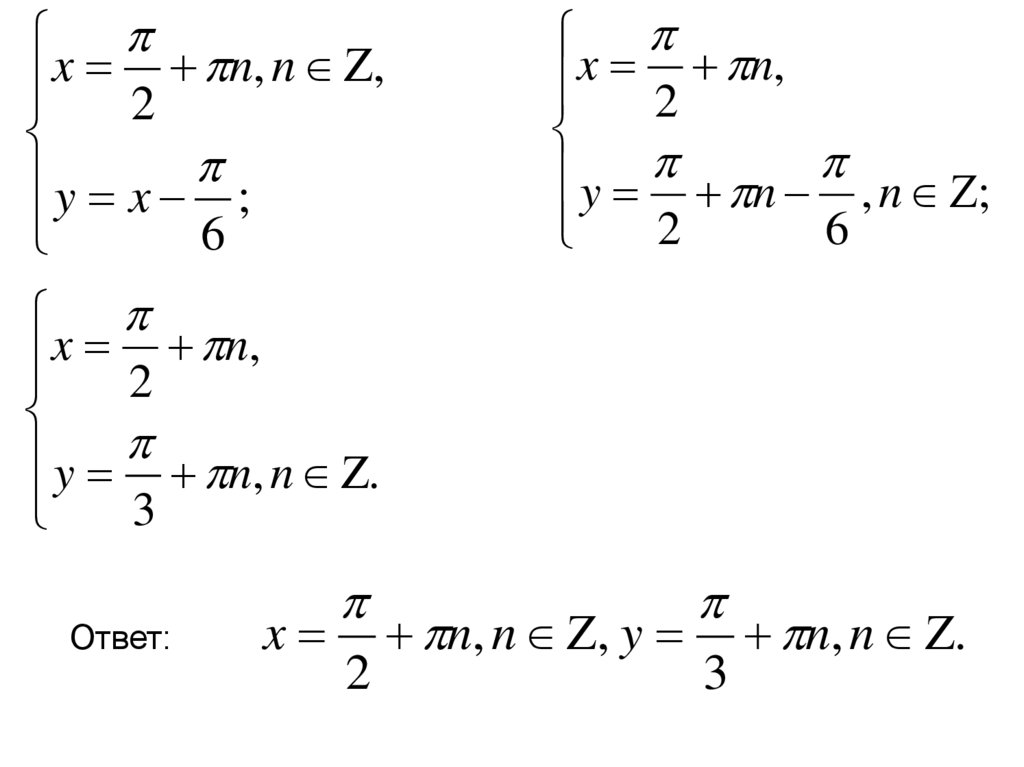


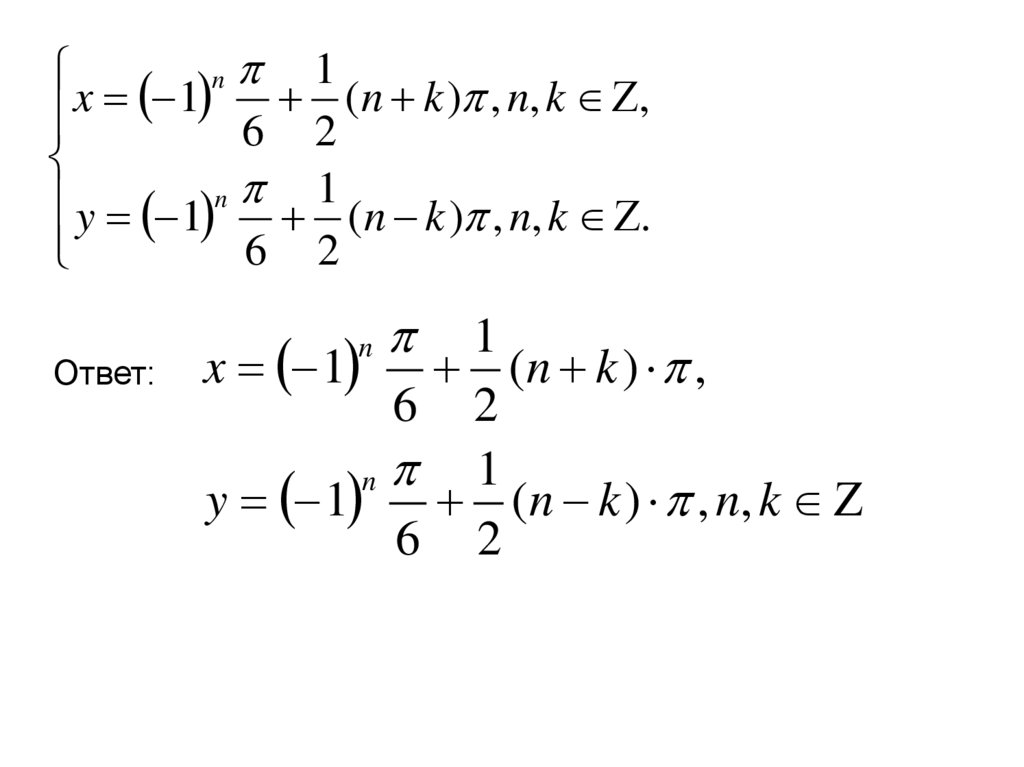
 mathematics
mathematics








