Similar presentations:
Решение тригонометрических уравнений
1. Решение тригонометрических уравнений
2.
Формула нахождения корней уравнения видаsin x = a?
х =( - 1) arcsin a +p n, n Z
n
Формула нахождения корней уравнения вида
cos x = a?
x = arccos a +2p n, n Z
Формула нахождения корней уравнения вида
tg x = a?
x =arctga +p n, n Z
3. Решите уравнения:
1sin x =
2
3
cosx =2
2
sin x =2
tgx =-
3
2
cos x =
2
x =( - 1)
n
p
6
+p n, n Z
5p
x =
+2p n, n Z
6
x =( - 1)
x =-
n +1
p
3
p
p
+p n, n Z
4
+p n, n Z
x = +2p n, n Z
4
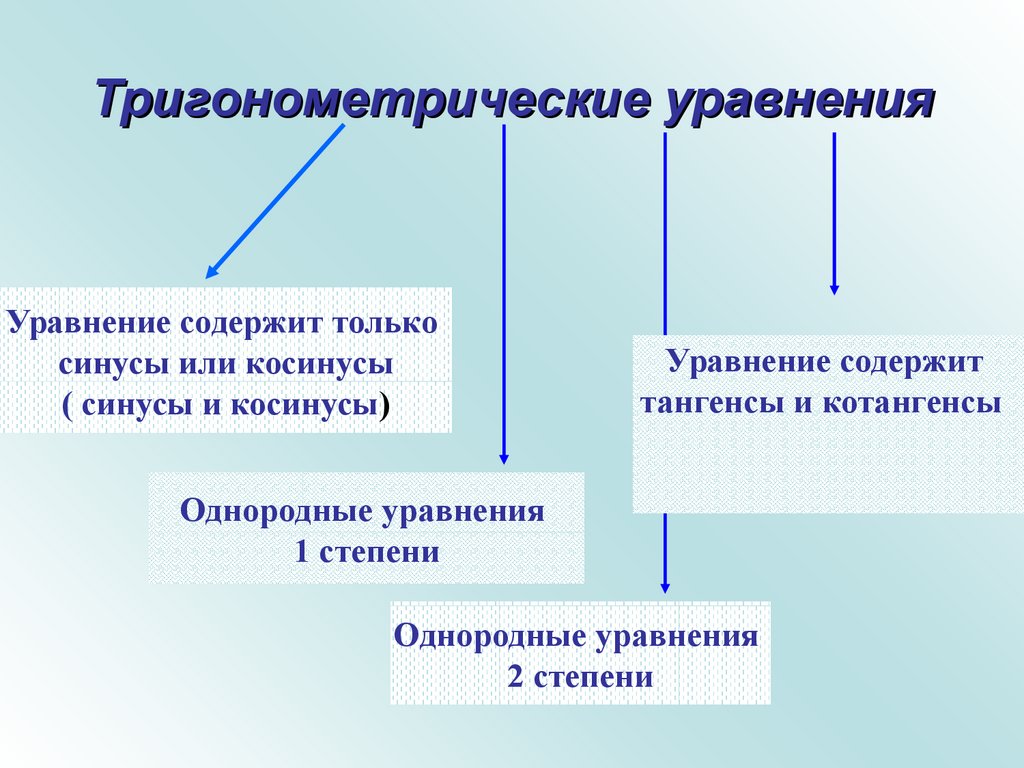
4. Тригонометрические уравнения
Уравнение содержит толькосинусы или косинусы
( синусы и косинусы)
Уравнение содержит
тангенсы и котангенсы
Однородные уравнения
1 степени
Однородные уравнения
2 степени
5. Уравнение содержит только синусы или косинусы ( синусы и косинусы)
2a sin x +b sin x +c =0
2
a cos x +b cos x +c =0
2
sin x =t
cos x =t
at +bt +c =0
6. Уравнение содержит только синусы или косинусы ( синусы и косинусы)
cos x) +b cos x +c =0a( 1 -sin
22
- sinx x )+
a ( 1cos
b sin x +c =0
2 2
2
cos x =t
sin x =t
at +bt +c =0
7.
Однородные уравненияa sin x a sin x cos x a cos x 0
n
0
n 1
n
1
n
Сумма показателей степеней при sin
x и cos x
n
у
всех
слагаемых
уравнения
Разделим cos
на x такого
Получим:
равна
n.
.
n
n 1
a tg x a tg x a 0
0
1
n
8.
первойстепени
a
+b
=0 b
tgx=- a
a
x=arctg (
b
k
Z
|:cos
x
)+πk,
9.
aa
второй
степени
+b
=0
+b
=0
+c |:
+c
10. Уравнение содержит тангенсы и котангенсы
2atg x +btgx +c =0
tgx =t
2
at +bt +c =0
atgx +bctgx +c =0
1
ctgx =
tgx
b
tgx =t
atgx +
+c =0
tgx
b
at + +c =0
t
11.
Методы решениятригонометрических уравнений
Указать метод решения уравнения:
2
sin x - 5sin x +4 =0
sin x = t , t [1;-1]
t 2 - 5t +4 =0;
D =9;
tпосторонний
1 =4;
корень
t2 =1
sin x =1
p
x=
2
+2p n, n Z
12.
Методы решениятригонометрических уравнений
Указать метод решения уравнения:
2
2
sin x - 7sin x cos x +10cos x =0
Однородное уравнение второй степени, делим на cos²x.
tg 2 x - 7tgx +10 =0;
tgx =t ;
t 2 - 7t +10 =0;
D =9;
t1 =5;
t2 =2;
tgx =5
tgx =2
x =arctg 5 +p n; n Z
x =arctg 2 +p k , k Z
13.
Методы решениятригонометрических уравнений
Указать метод решения уравнения:
sin x +cos x =0
Однородное уравнение первой степени, делим на cosx.
tgx +1 =0;
tgx =- 1;
p
x =+p n, n Z
4
14.
Методы решениятригонометрических уравнений
Указать метод решения уравнения:
2
8cos x +sin x +1 =0
Уравнение содержащие синус и косинус, заменяем cos²x на 1 - sin²x
2
8 - 8sin x +sin x +1 =0;
8sin 2 x - sin x - 9 =0;
sin x =t , t [ - 1;1]
D =289;
9
tпосторонний
=
корень
1
8
t2 =- 1
sin x =- 1
x =-
p
2
+p n, n Z
;







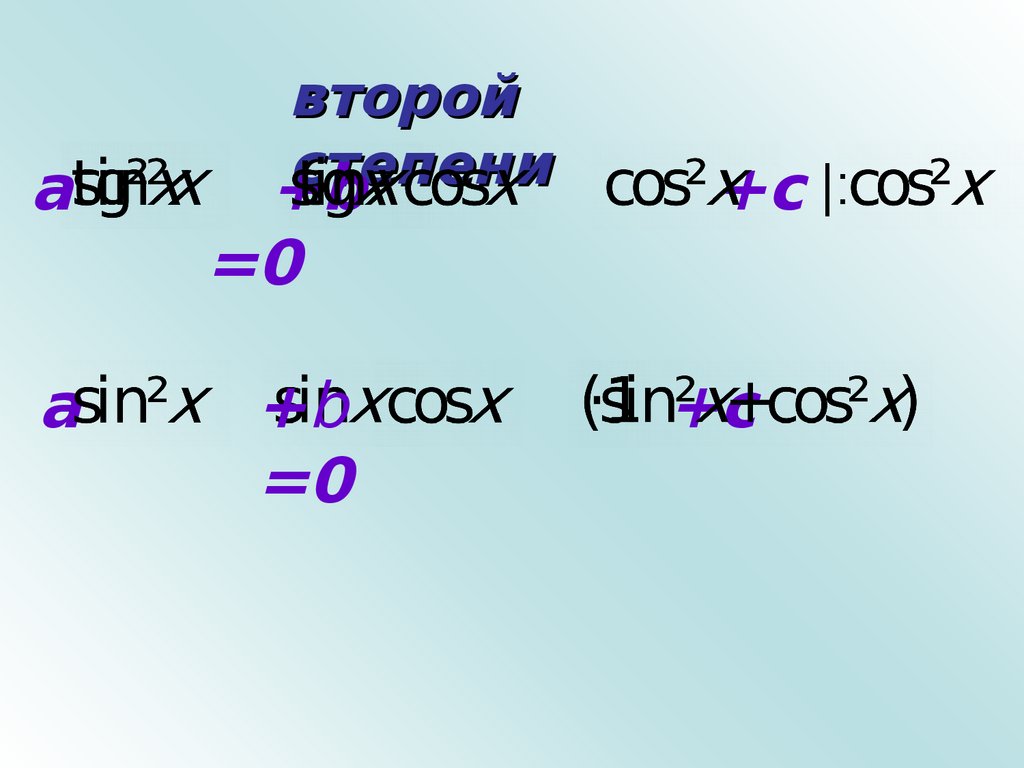





 mathematics
mathematics








