Решение тригонометрических неравенств.10 класс ( профиль)

1. «Решение тригонометрических неравенств» 10 класс ( профиль)

Презентация подготовлена учителем
математики
МОУ «СОШ №1 р.п. Новые Бурасы»
Боровиковой Е.И.
с использованием интерактивной доски

2.

Решить
неравенство:sin t>1/2
5п/6
у
y=1/2
п/6
Х
Ответ: п/6+2пк<t<5п/6 + 2пк,кєz
Решение: Учтем, что sin t – это ордината точки М (t) числовой окружности.
Значит, нам нужно найти на числовой окружности точки с ординатой
у>1/2 и записать, каким числам t они соответствуют.

3.

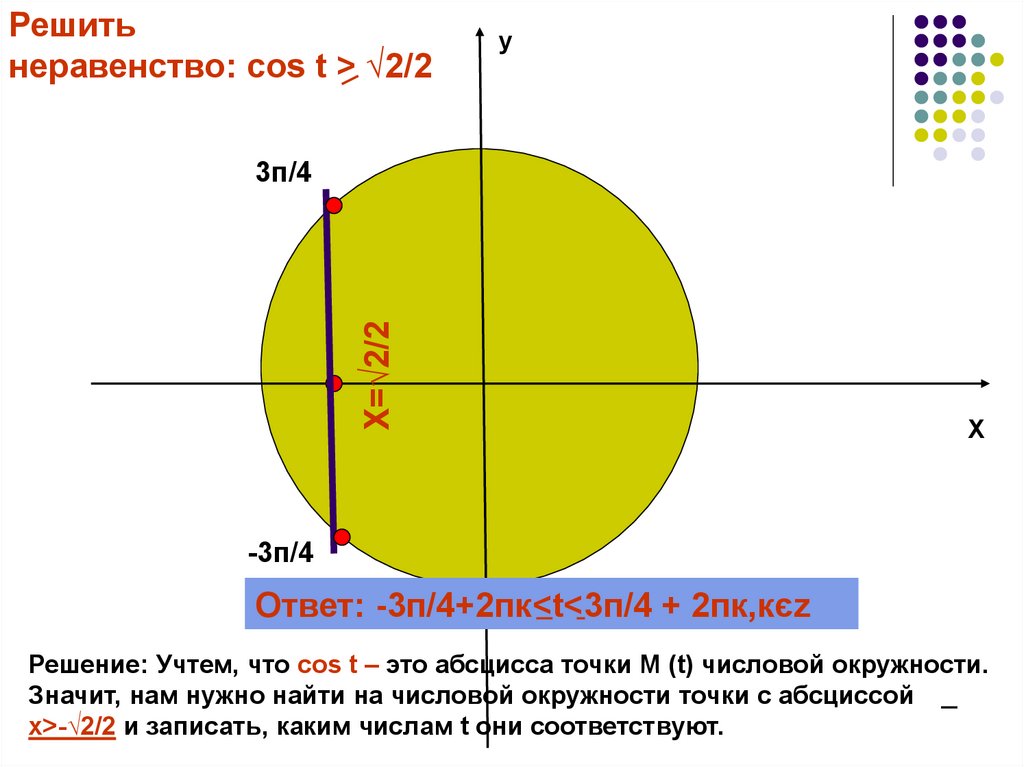
Решить
неравенство: сos t > √2/2
у
Х=√2/2
3п/4
Х
-3п/4
Ответ: -3п/4+2пк<t<3п/4 + 2пк,кєz
Решение: Учтем, что сos t – это абсцисса точки М (t) числовой окружности.
Значит, нам нужно найти на числовой окружности точки с абсциссой
х>-√2/2 и записать, каким числам t они соответствуют.

4.

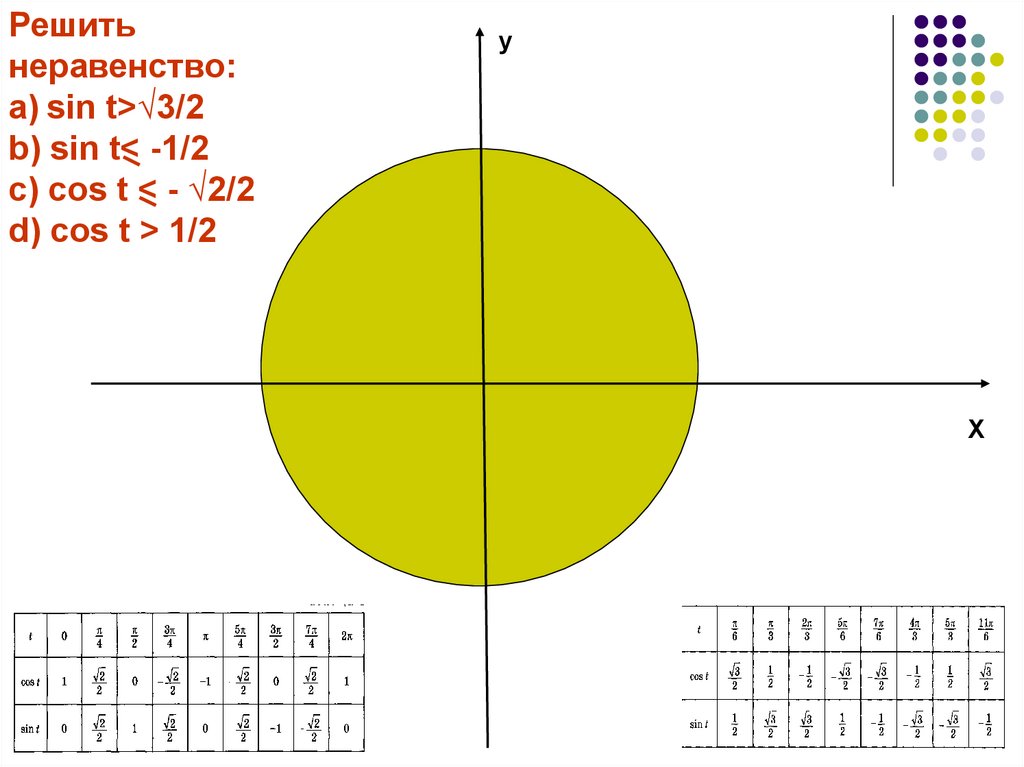
Решить
неравенство:
a) sin t>√3/2
b) sin t< -1/2
c) сos t < - √2/2
d) сos t > 1/2
у
Х

5.

У
Решить
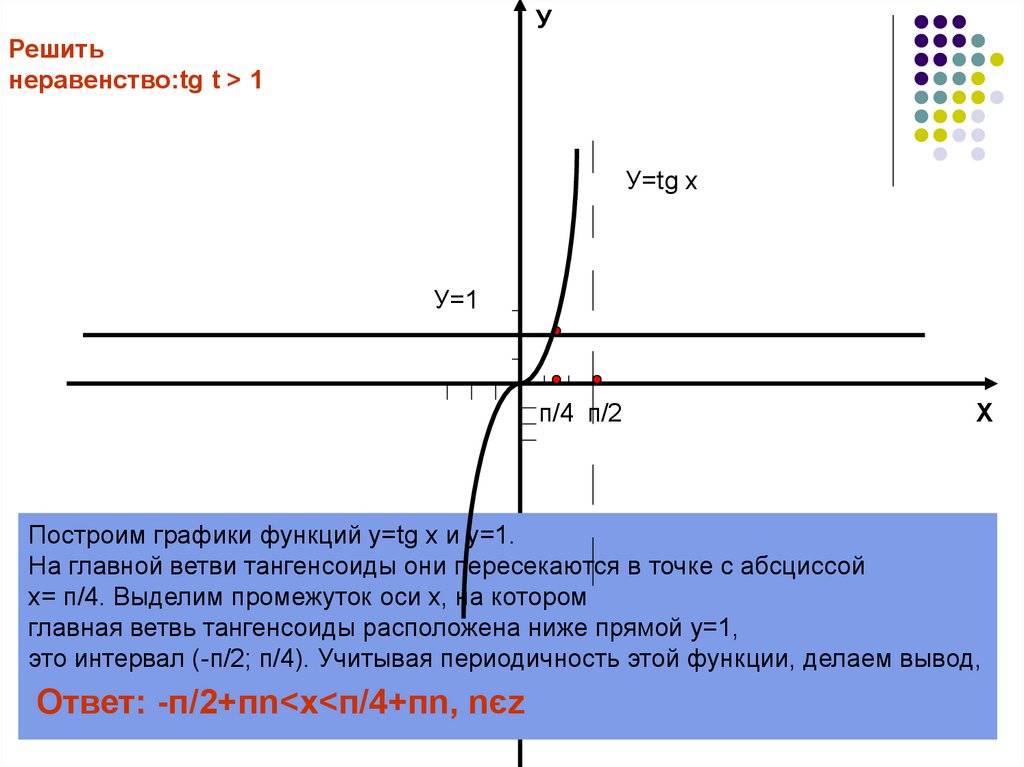
неравенство:tg t > 1
У=tg x
У=1
п/4 п/2
Х
Построим графики функций у=tg x и у=1.
На главной ветви тангенсоиды они пересекаются в точке с абсциссой
х= п/4. Выделим промежуток оси х, на котором
главная ветвь тангенсоиды расположена ниже прямой у=1,
это интервал (-п/2; п/4). Учитывая периодичность этой функции, делаем вывод,
Ответ: -п/2+пn<x<п/4+пn, nєz
Ответ: -п/2+пn<x<п/4+пn, nєz

6.

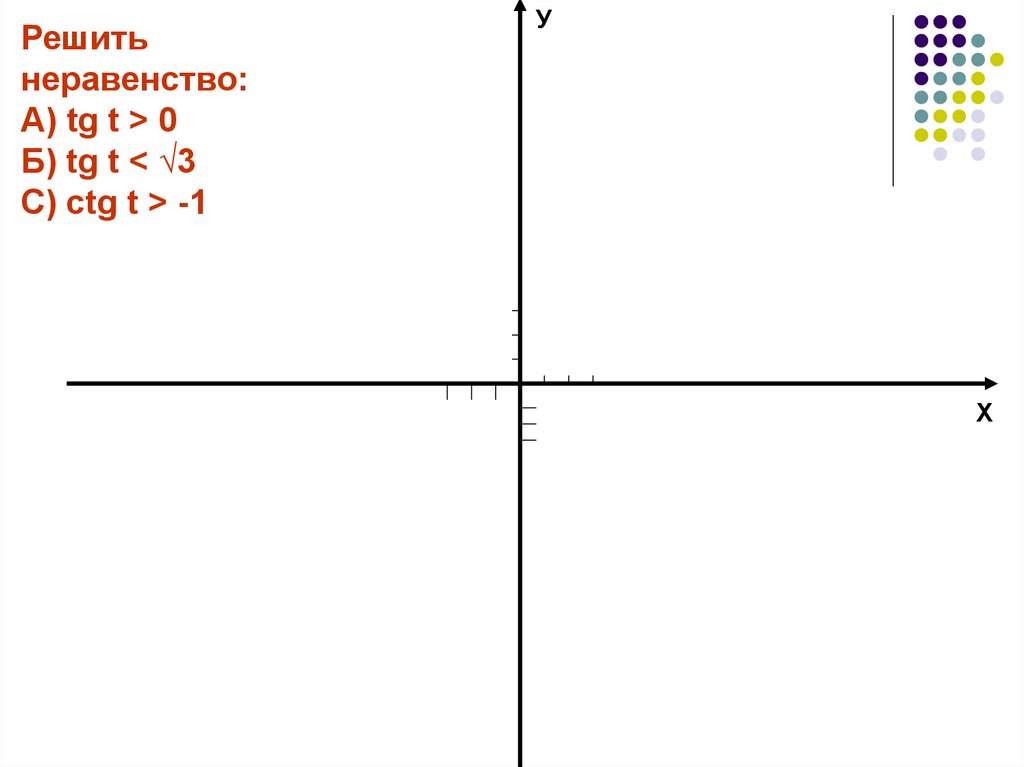
Решить
неравенство:
А) tg t > 0
Б) tg t < √3
C) ctg t > -1
У
Х

7. ПОДГОТОВКА К К/Р

8.

НЕКОТОРЫЕ ФОРМУЛЫ ПРИВЕДЕНИЯ