Similar presentations:
Повторение курса алгебры 10 класса
1.
ПовторениеАлгебра и начала
анализа (ЕМН)
10 класс
2.
Разделы 1 полугодияРаздел 10.1А: Функция, ее свойства и график
Раздел 10.1В: Тригонометрические функции
Раздел 10.1.С: Обратные
тригонометрические функции
Раздел 10.2.А: Тригонометрические
уравнения
Раздел 10.2.В: Тригонометрические
неравенства.
Раздел 10.2.С: Вероятность
3.
Цель урокаПовторить разделы:
Функция, ее свойства и график
Тригонометрические функции
Обратные тригонометрические функции
Тригонометрические уравнения
Тригонометрические неравенства.
4.
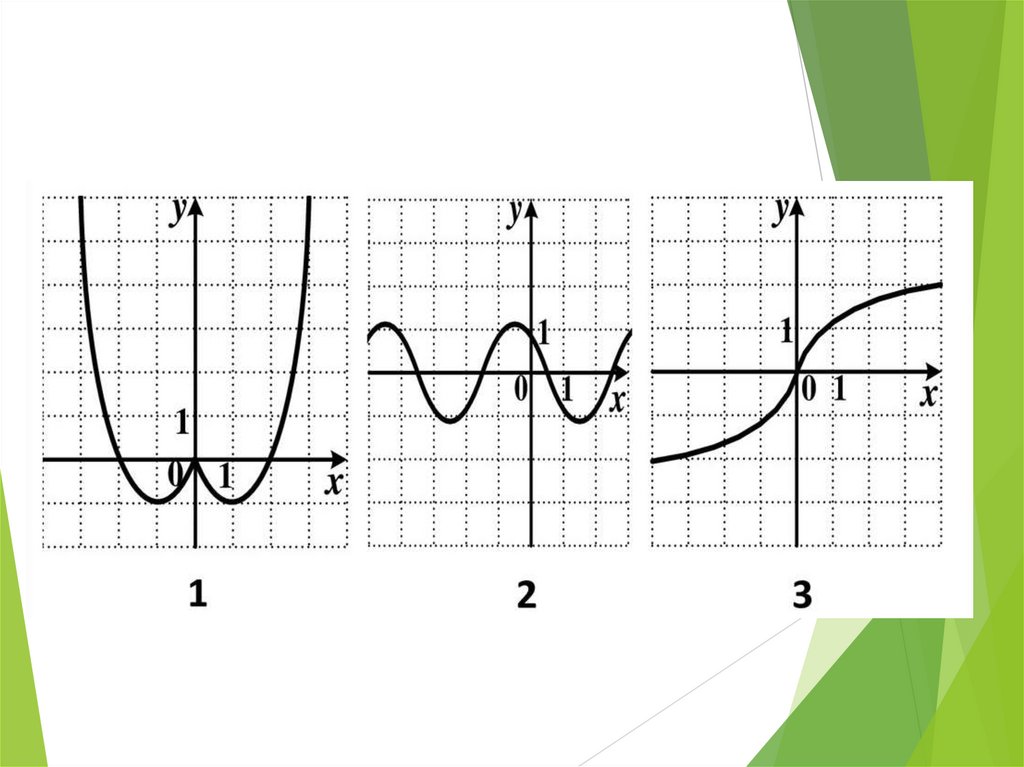
ЗаданиеПо графику определите:
А) Область определения функции. Является
ли функция непрерывной?
B) Область значений функции.
C) Является ли функция ограниченной?
D) Является ли функция периодической?
E) Является ли функция четной (нечетной)?
Объясните.
F) Определите промежутки монотонности
функции, экстремумы.
5.
6.
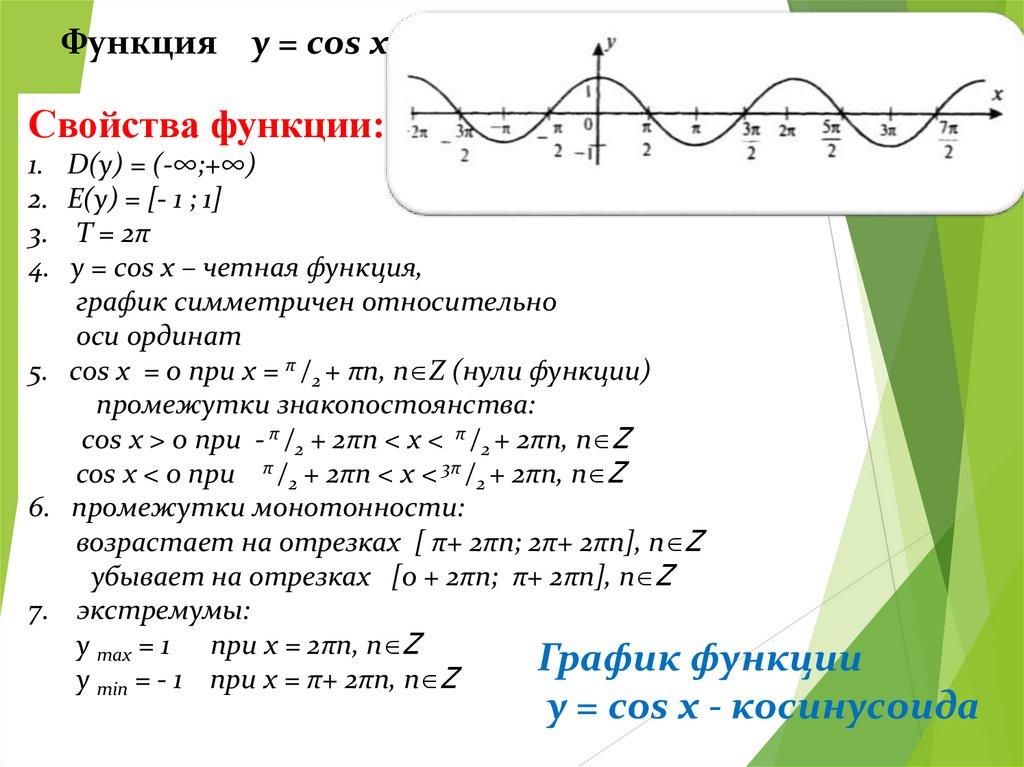
Функция y = cos xСвойства функции:
1.
2.
3.
4.
D(у) = (-∞;+∞)
E(у) = [- 1 ; 1]
T = 2π
y = cos x – четная функция,
график симметричен относительно
оси ординат
5. cos x = 0 при х = π /2 + πn, n Z (нули функции)
промежутки знакопостоянства:
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, n Z
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, n Z
6. промежутки монотонности:
возрастает на отрезках [ π+ 2πn; 2π+ 2πn], n Z
убывает на отрезках [0 + 2πn; π+ 2πn], n Z
7. экстремумы:
y max = 1 при х = 2πn, n Z
График функции
y min = - 1 при х = π+ 2πn, n Z
y = cos x - косинусоида
7.
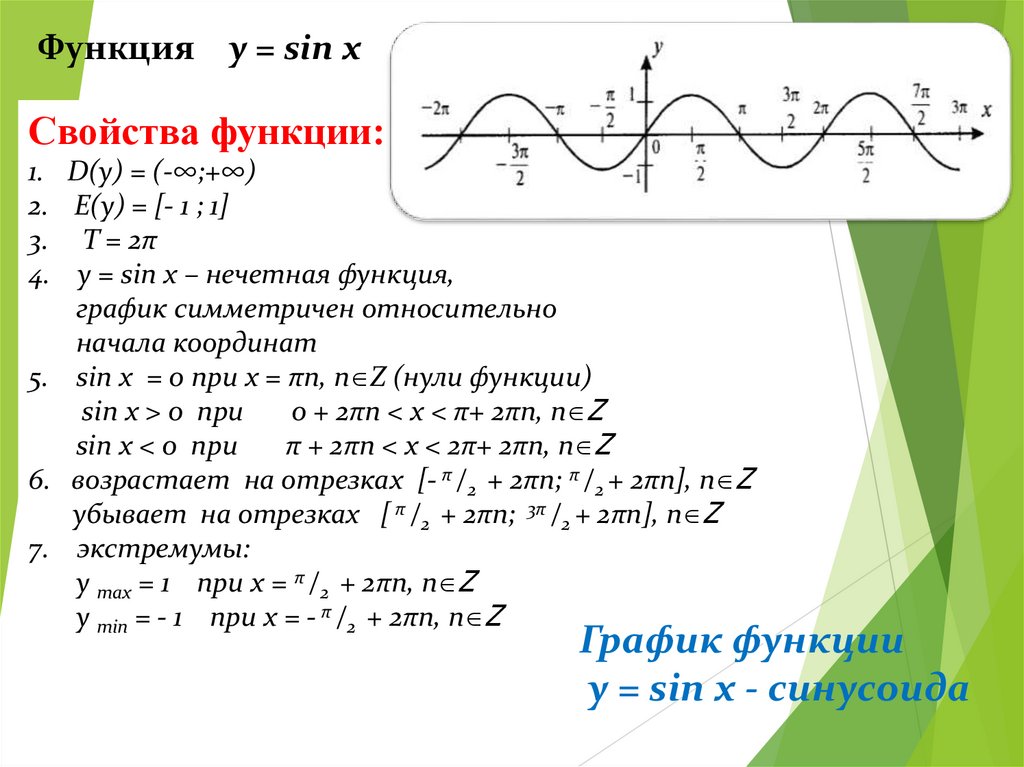
Функция y = sin xСвойства функции:
1. D(у) = (-∞;+∞)
2. E(у) = [- 1 ; 1]
3. T = 2π
4. y = sin x – нечетная функция,
график симметричен относительно
начала координат
5. sin x = 0 при х = πn, n Z (нули функции)
sin x > 0 при
0 + 2πn < x < π+ 2πn, n Z
sin x < 0 при
π + 2πn < x < 2π+ 2πn, n Z
6. возрастает на отрезках [- π /2 + 2πn; π /2 + 2πn], n Z
убывает на отрезках [ π /2 + 2πn; 3π /2 + 2πn], n Z
7. экстремумы:
y max = 1 при х = π /2 + 2πn, n Z
y min = - 1 при х = - π /2 + 2πn, n Z
График функции
y = sin x - синусоида
8.
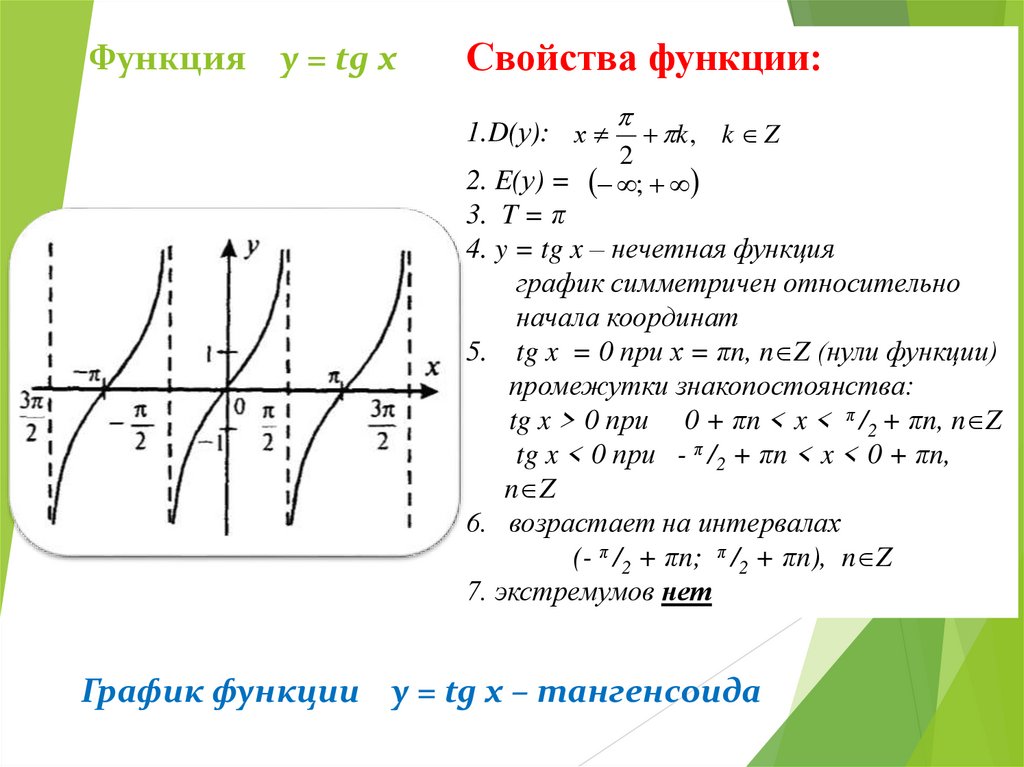
Функция y = tg xСвойства функции:
1.D(у): х
k , k Z
2
2. E(у) = ;
3. T = π
4. y = tg x – нечетная функция
график симметричен относительно
начала координат
5. tg x = 0 при х = πn, n Z (нули функции)
промежутки знакопостоянства:
tg x > 0 при 0 + πn < x < π /2 + πn, n Z
tg x < 0 при - π /2 + πn < x < 0 + πn,
n Z
6. возрастает на интервалах
(- π /2 + πn; π /2 + πn), n Z
7. экстремумов нет
График функции y = tg x – тангенсоида
9.
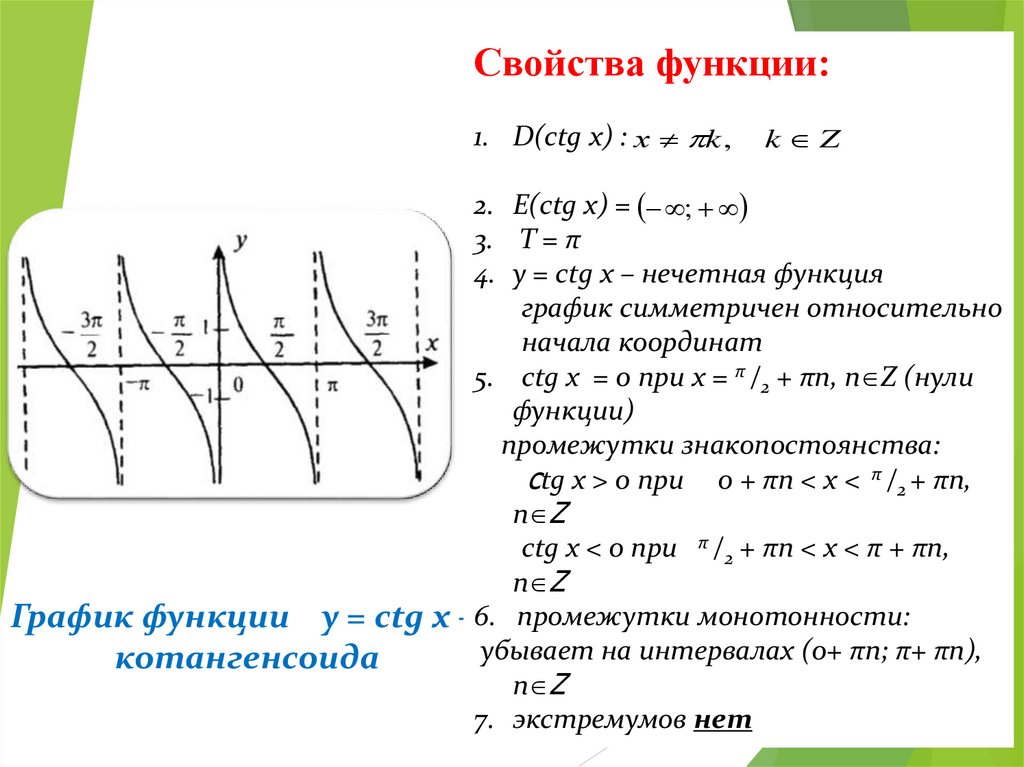
Свойствафункции:
Функция
y = ctg x
1. D(ctg x) : х k ,
k Z
2. E(ctg x) = ;
3. T = π
4. y = ctg x – нечетная функция
график симметричен относительно
начала координат
5. ctg x = 0 при х = π /2 + πn, n Z (нули
функции)
промежутки знакопостоянства:
ctg x > 0 при 0 + πn < x < π /2 + πn,
n Z
ctg x < 0 при π /2 + πn < x < π + πn,
n Z
График функции y = ctg x –6. промежутки монотонности:
убывает на интервалах (0+ πn; π+ πn),
котангенсоида
n Z
7. экстремумов нет
10.
Функция y = arcsin x и ее свойстваЕсли |а| ≤ 1, то arcsin а – это такое число
из отрезка [-π/2; π/2], синус которого
равен а.
Если |а| ≤ 1, то
arcsin а = t
sin (arcsin a) = a
sin t = а,
-π/2 ≤ t ≤ π/2;
11.
Функция y = arcsin x и ее свойства1. D(y) = [-1; 1].
2. E(y) = [-π/2; π/2].
3. arcsin (-x) = - arcsin x – функция
нечетная.
4. Функция возрастает на [-1; 1].
5. Функция непрерывна.
sin-1x=arcsin x
12.
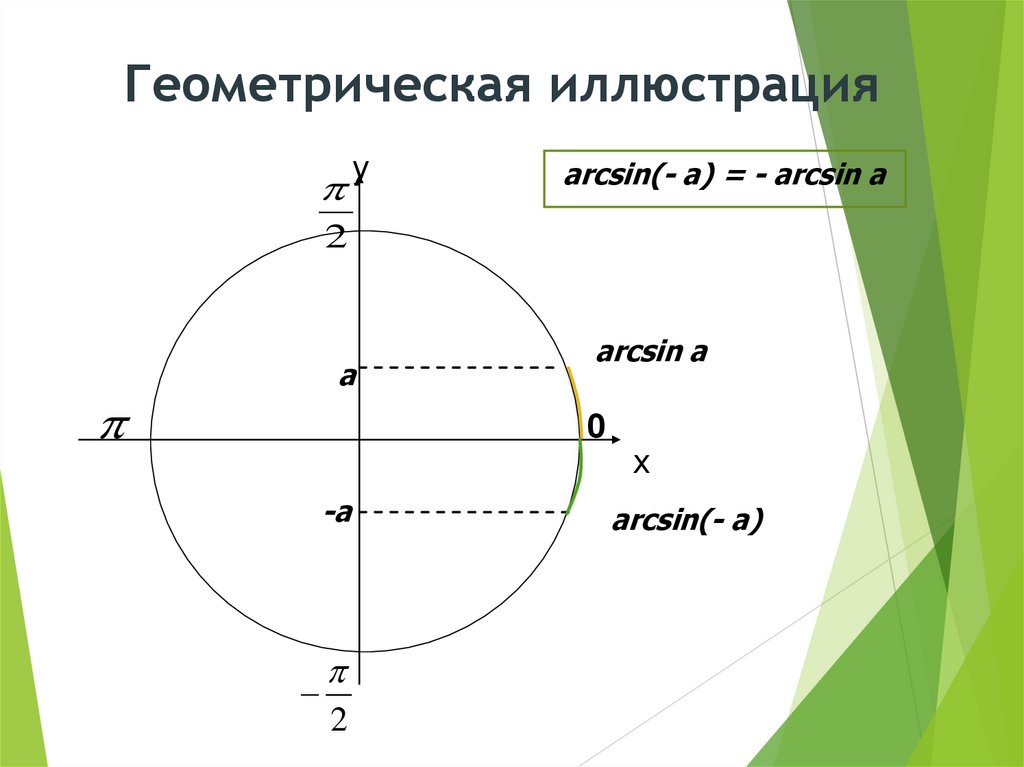
Геометрическая иллюстрацияу
arcsin(- a) = - arcsin a
2
a
arcsin a
0
-a
2
х
arcsin(- a)
13.
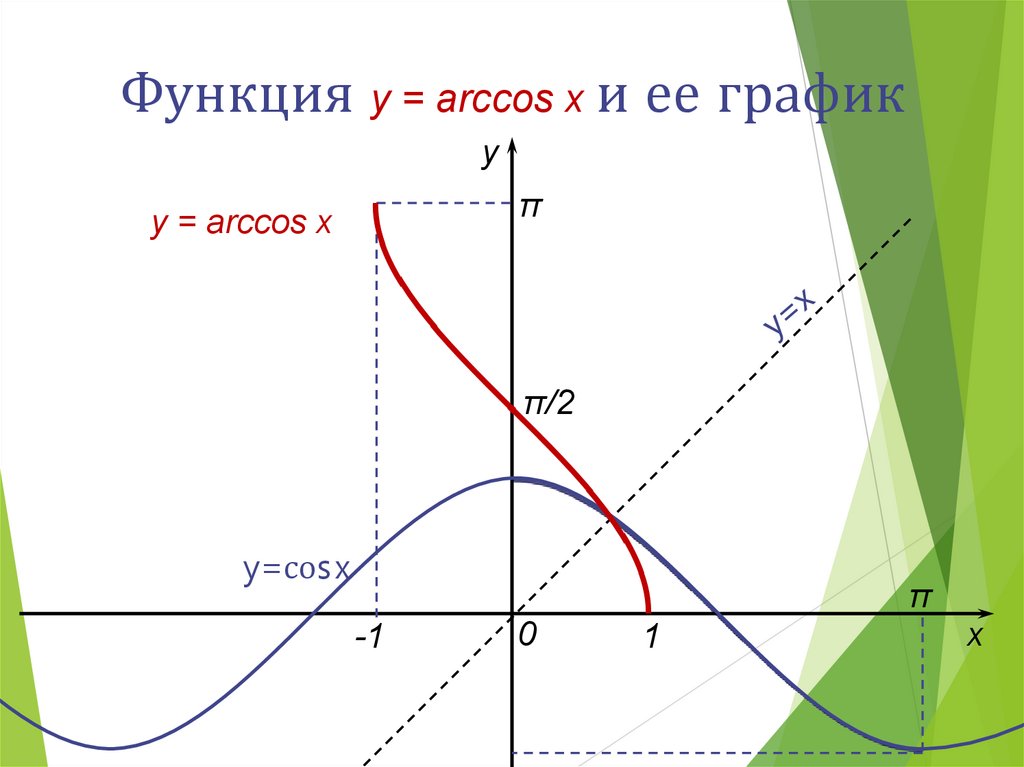
Функция y = arccos x и ее графику
π
y = arccos x
π/2
y=соs x
π
-1
0
1
х
14.
Функция y = arccos x и ее свойства1. D(y) = [-1; 1].
2. E(y) = [0; π].
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на [-1; 1].
5. Функция непрерывна.
cos-1x=arccos x
15.
Функция y = arccos x и ее свойстваЕсли |а| ≤ 1, то arccos а – это такое число
из отрезка [0; π], косинус которого равен
а.
Если |а| ≤ 1, то
arccos а = t
cos t = а,
0 ≤ t ≤ π;
cos (arccos a) = a
arccos (-a) = π – arccos a, где 0 ≤ а ≤ 1
16.
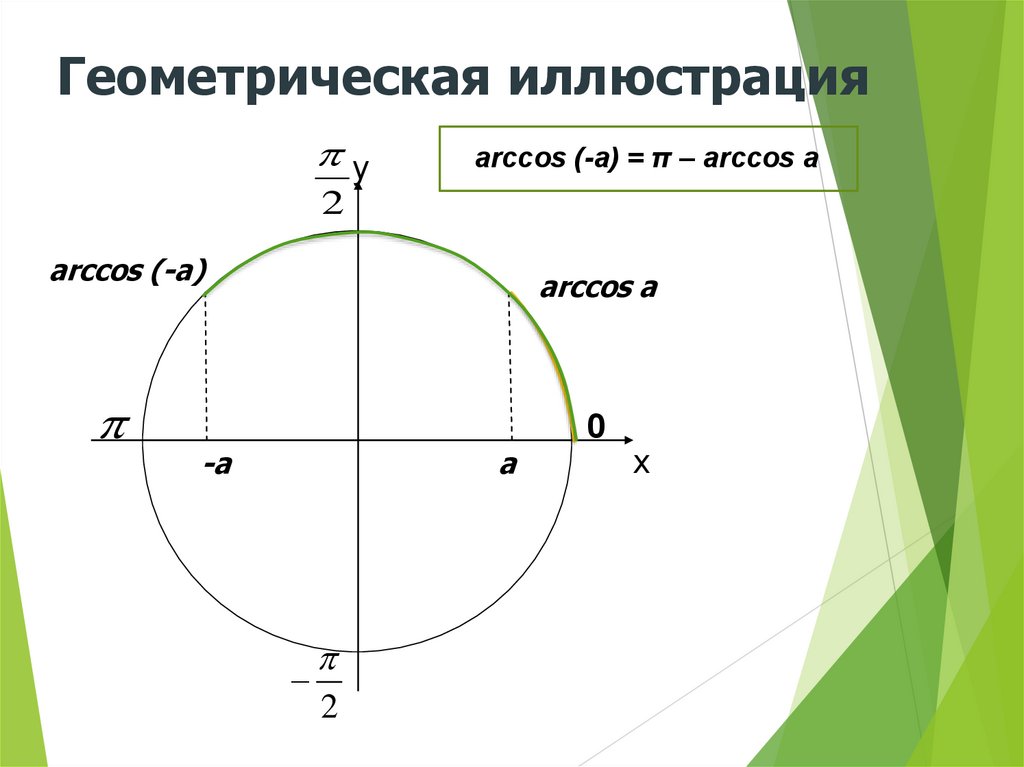
Геометрическая иллюстрацияу
arccos (-a) = π – arccos a
2
arccos (-a)
arccos a
-a
a
2
0
х
17.
Работаем устноarcsin 1
arcsin 0
arccos 1
arccos 0
2
arcsin
2
1
arcsin
2
1
arccos
2
1
arccos
3
arcsin(-x) = - arcsinx
1
arcsin( )
2
1
arccos( )
2
3
2
arcsin( )
arccos(
)
2
2
arccos(-x) = - arccosx
18.
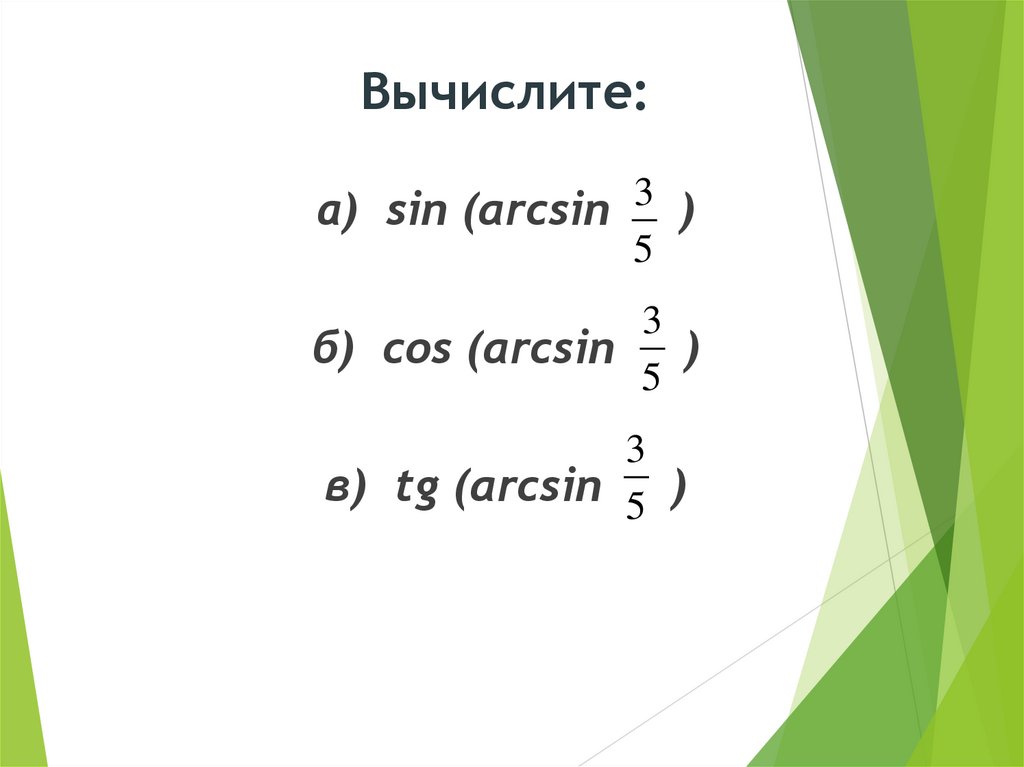
Вычислите:а) sin (arcsin 3 )
5
3
б) cos (arcsin
)
5
3
в) tg (arcsin 5 )
19.
20.
простейшие тригонометрическиеуравнения
sin x a
x arcsin a 2 n, п Z
x arcsin a 2 n, n Z .
Частные случаи:
sin x 0
x n, n Z
sin x 1
x
2
2 n, n Z
sin x 1
x
2
2 n, n Z
21.
простейшие тригонометрическиеуравнения.
cos x a
x arccos a 2 n, n Z
cos x 0
x
2
n, n Z
Частные случаи:
cos x 1
cos x 1
x 2 n, n Z
x 2 n, n Z
22.
простейшие тригонометрическиеуравнения
tgx a
x arctga n, n Z
Частные случаи:
tgx 1
tgx 0
x n, n Z
x
4
n, n Z
tgx 1
x
4
n, n Z
23.
простейшие тригонометрическиеуравнения
ctgx a
x arcctga n, n Z
ctgx 0
x
2
n, n Z
Частные случаи:
ctgx 1
x
4
n, n Z
ctgx 1
3
x
n, n Z
4
24.
Задание: а)Решить уравнениеб)Указать корни уравнения,
удовлетворяющие условию.
1.а)
2.а)
3.а)
4.а)
x
x
x
x
3 sin cos cos sin sin 2 x x ;
2
2
2
2
2
x
3
x
4 cos 1 sin x sin 2 x
2 ; 2
2
3
x ; 2
2
2
3 sin x cos
x
2
2
13
6tg x
12 0
cos x
3 7
x ;
2 2
3
cos
2 x cos x 0
2
x 2 ;
2
2
5.а)
25.
Решить неравенство:2
cos x
2
3
4
2
3
arccos(
)
2
4
4
1. Отметим на оси абсцисс
интервал x 2 / 2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Запишем общее решение
неравенства.
y
1
1
-1
2/2
3
4
0
x
-1
3
3
2 n x
2 n, n Z
4
4
26.
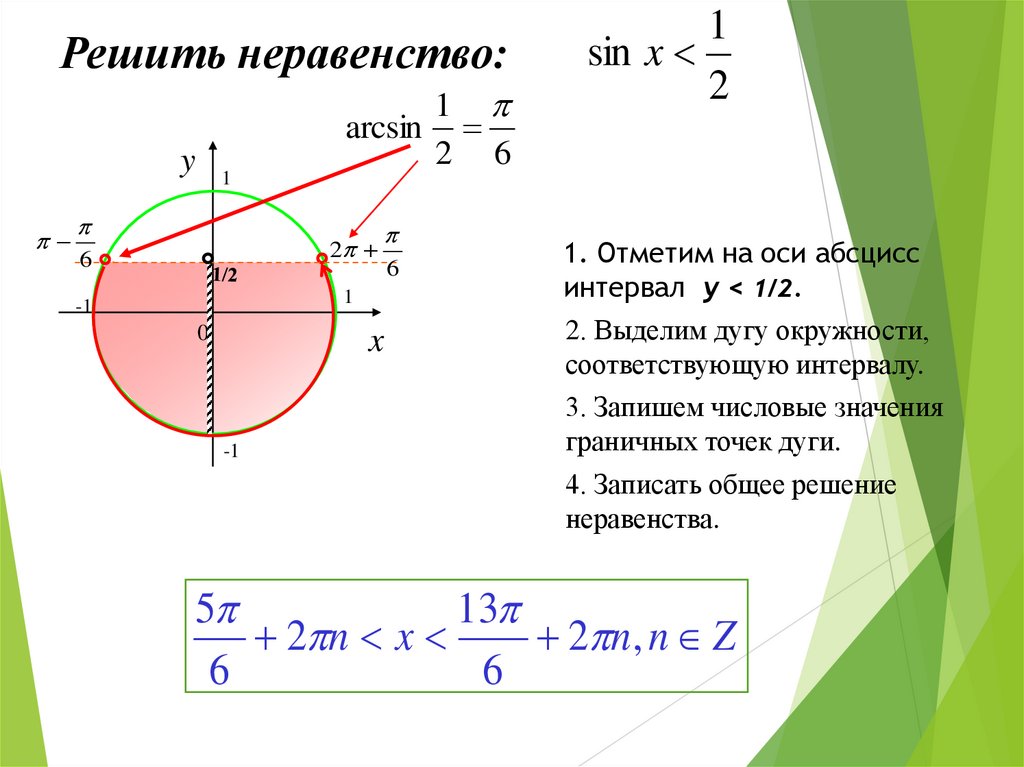
Решить неравенство:y
1
1
arcsin
2 6
6
2
-1
1
0
x
-1
6
1
sin x
2
1. Отметим на оси абсцисс
интервал y < 1/2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
5
13
2 n x
2 n, n Z
6
6
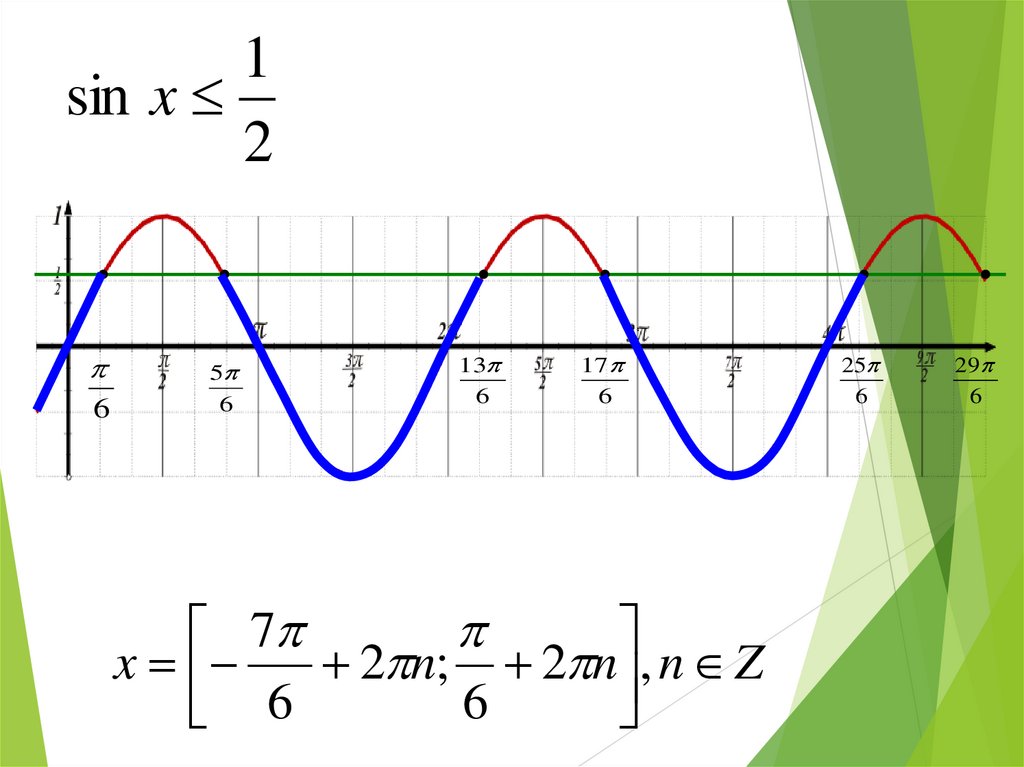
27.
1sin x
2
6
5
6
13
6
17
6
7
x
2 n; 2 n , n Z
6
6
25
6
29
6
28.
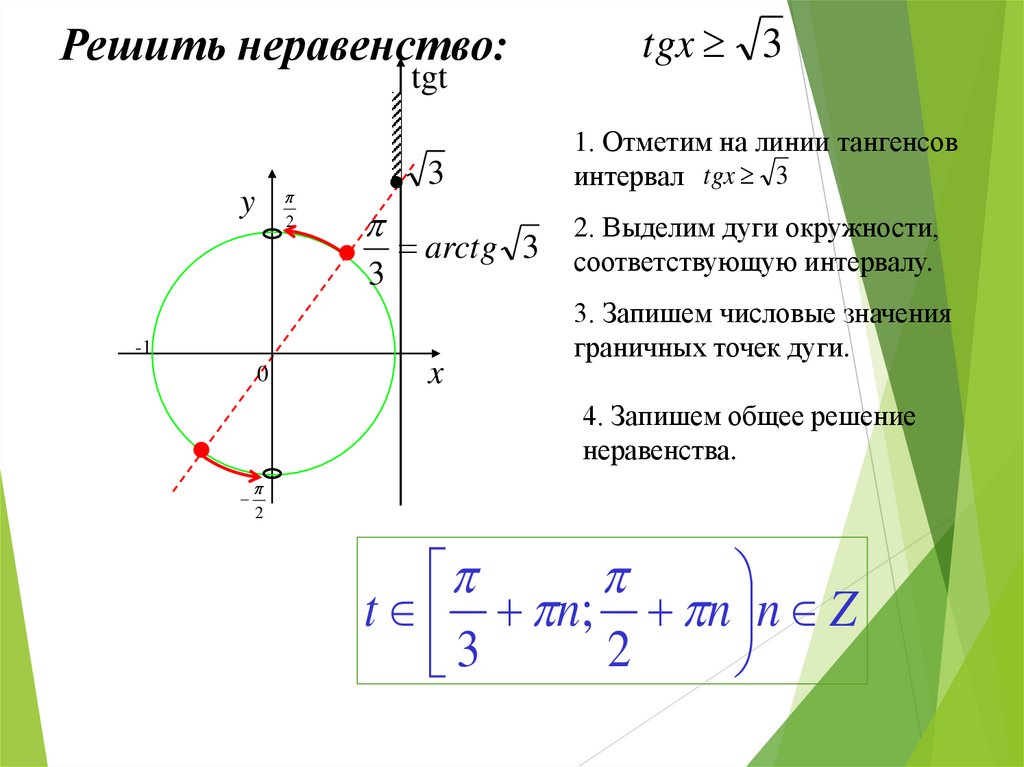
Решить неравенство:tgt
2
y
3
3
arctg 3
-1
0
x
tgx 3
1. Отметим на линии тангенсов
интервал tgx 3
2. Выделим дуги окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Запишем общее решение
неравенства.
2
t n; n n Z
2
3
29.
1. Решите неравенство, применяятригонометрические формулы:
а) 4sin3x∙cos3x> 2
b)
sin 3

















 mathematics
mathematics








