Тригонометрические неравенства

1. Тригонометрические неравенства

cos t a(cos t a)
cos t a(cos t a)
Тригонометрические
tgt a(ctgt a)
неравенства
sin t a(sin t a)
sin t a(sin t a)
ctgt a(tgt a)
МОУ «Тверская гимназия №6»
г.Тверь
Аграчева Юлия Леонидовна

2.

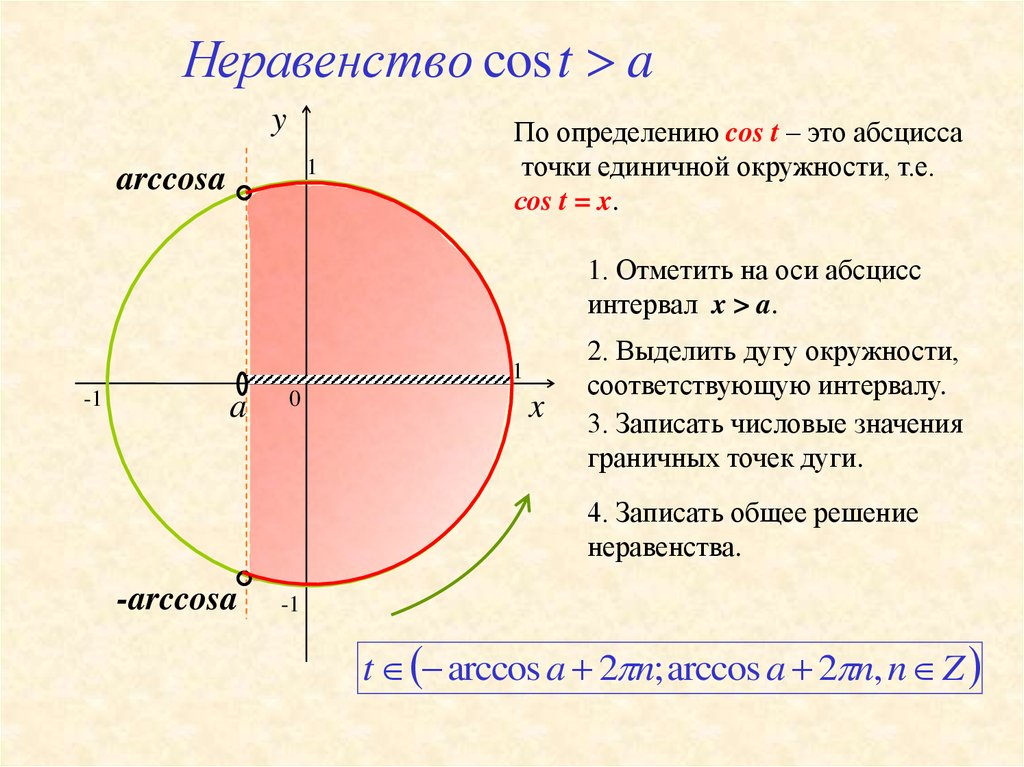
Неравенство cos t a
y
1
arccosa
По определению cos t – это абсцисса
точки единичной окружности, т.е.
сos t = x.
1. Отметить на оси абсцисс
интервал x > a.
1
-1
a
0
x
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
-arccosa
-1
t arccos a 2 n; arccos a 2 n, n Z

3.

Решить неравенство:
2
cos x
2
3
4
2
3
arccos(
)
2
4
4
1. Отметим на оси абсцисс
интервал x 2 / 2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Запишем общее решение
неравенства.
y
1
1
-1
2/2
3
4
0
x
-1
3
3
2 n x
2 n, n Z
4
4

4.

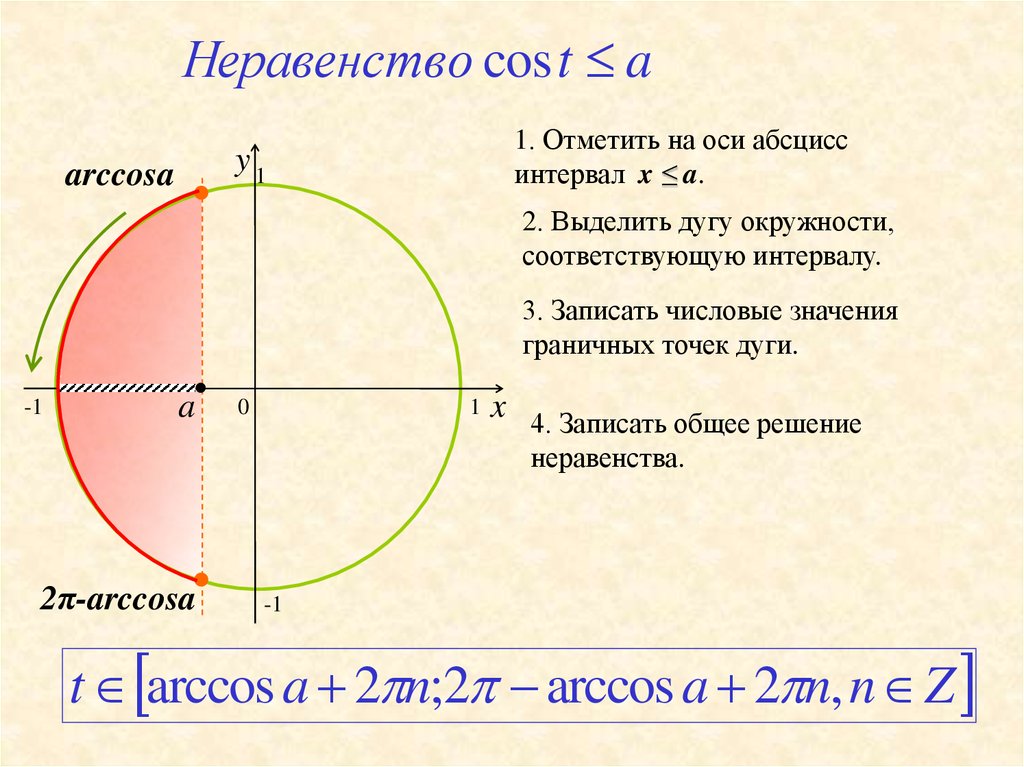
Неравенство cos t a
1. Отметить на оси абсцисс
интервал x ≤ a.
y1
arccosa
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
-1
a
0
1
x 4. Записать общее решение
неравенства.
2π-arccosa
-1
t arccos a 2 n;2 arccos a 2 n, n Z

5.

1
cos x
2
Решить неравенство:
y
1
arccos
3
1
-1
0
1/2
x
-1
5
2
3
3
1
2 3
1. Отметим на оси абсцисс
интервал x < 1/2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Запишем общее решение
неравенства.
5
2 n x
2 n, n Z
3
3

6.

Неравенство sin t a
По определению sin t – это ордината
точки единичной окружности, т.е.
sin t = y.
y
1
π-arcsina
1. Отметить на оси ординат
интервал y ≤ a.
a
-1
0
1
x
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
-1
4. Записать общее решение
неравенства.
t arcsin a 2 n; arcsin a 2 2 n, n Z

7.

Решить неравенство:
y
1
1
arcsin
2 6
6
2
-1
1
0
x
-1
6
1
sin x
2
1. Отметим на оси абсцисс
интервал y < 1/2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
5
13
2 n x
2 n, n Z
6
6

8.

Неравенство sin t a
y
1
1. Отметить на оси ординат
интервал y > a.
π-arcsina
arcsina
a
-1
1
0
x
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
-1
t arcsin a 2 n; arcsin a 2 n, n Z

9.

Решить неравенство:
y
2
sin x
2
1. Отметим на оси абсцисс
интервал y 2 / 2.
1
2. Выделим дугу окружности,
соответствующую интервалу.
1
-1
0
5
4
x
2 / 2.
-1
2
arcsin( )
2
4
4
3. Запишем числовые значения
граничных точек дуги.
4. Запишем общее решение
неравенства.
2
arcsin(
)
2
4
5
2 n x
2 n, n Z
4
4

10.

Неравенство tgt a
tgt
1. Отметить на линии тангенсов
интервал tgt < a
2
y
2. Выделить дуги окружности,
соответствующую интервалу.
arctga
3. Записать числовые значения
граничных точек дуги.
-1
x
0
a
2
arctga
4. Записать общее решение
неравенства.
t n; arctga n n Z
2

11.

Неравенство tgt a
tgt
2
y
arctga
2. Выделить дуги окружности,
соответствующую интервалу.
-1
x
0
a
1. Отметить на линии тангенсов
интервал tgt > a
arctga
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
2
t arctga n; n n Z
2

12.

Решить неравенство:
tgt
2
y
3
3
arctg 3
-1
0
x
tgx 3
1. Отметим на линии тангенсов
интервал tgx 3
2. Выделим дуги окружности,
соответствующую интервалу.
3. Запишем числовые значения
граничных точек дуги.
4. Запишем общее решение
неравенства.
2
t n; n n Z
2
3

13.

Неравенство ctgt < a
y
a ctgt
arcctga
0
arcctga
0
x
1. Отметить на линии
котангенсов интервал ctgt < a
2. Выделить дуги окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
t arcctga n; n n Z

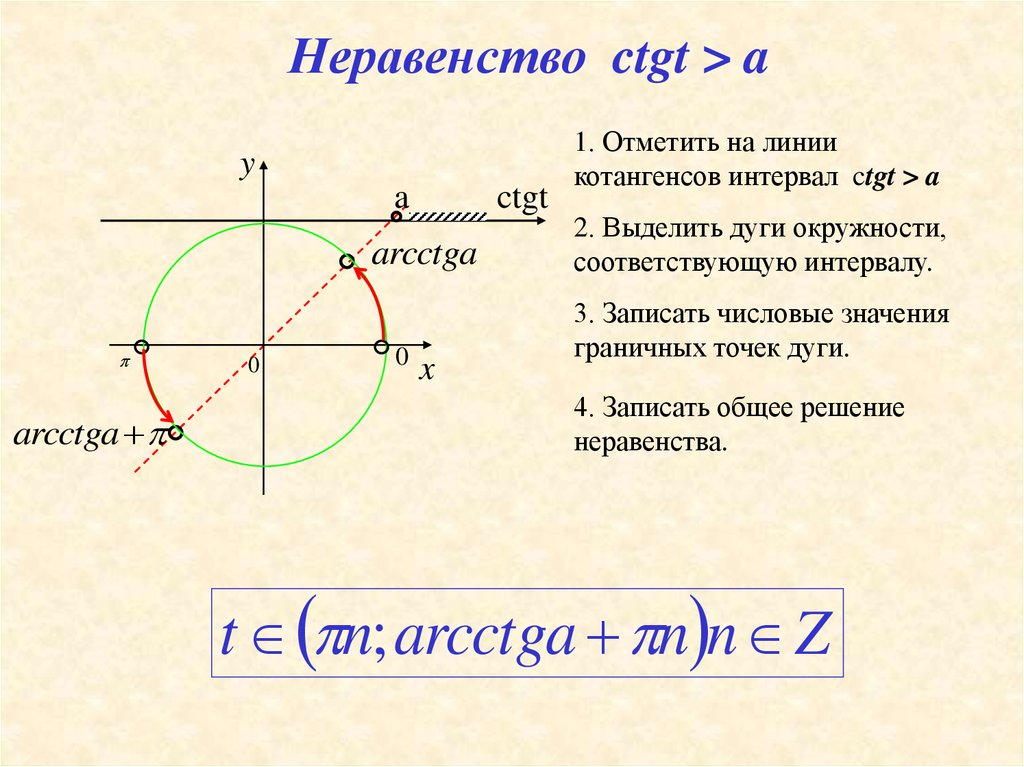
14.

Неравенство ctgt > a
y
a
ctgt
arcctga
arcctga
0
0
x
1. Отметить на линии
котангенсов интервал ctgt > a
2. Выделить дуги окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
t n; arcctga n n Z

15.

ctgx 3
Решить неравенство:
1. Отметить на линии
котангенсов интервал ctgx 3
y
3
ctgt
0
2. Выделить дуги окружности,
соответствующую интервалу.
0
x
3. Записать числовые значения
граничных точек дуги.
arcctg ( 3 )
6
4. Записать общее решение
неравенства.
t n; n n Z
6