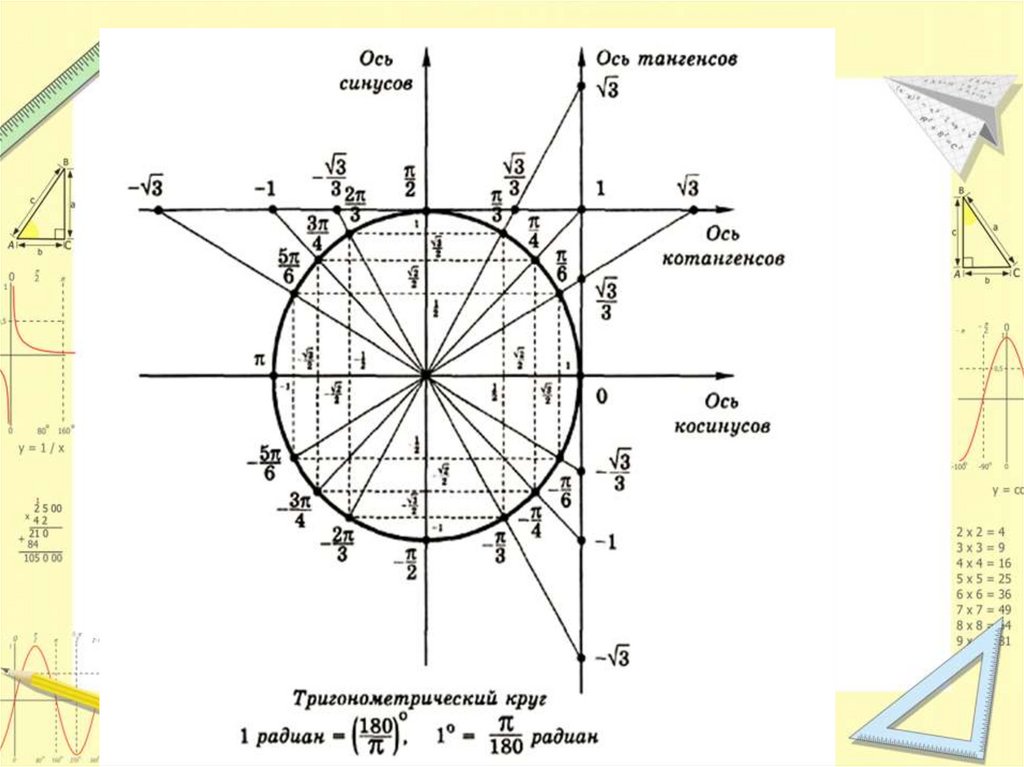
Similar presentations:
Тригонометрические неравенства
1. Решение простейших тригонометрических неравенств
МатематикаРешение простейших
тригонометрических
неравенств
Подготовила К.А.Куталова
2.
3.
4.
Запишите алгоритмырешения в тетрадь:
5. Неравенство cost > a
Неравенство cost > a-1
t1
y
a
0
-t1
1
x
1. Отметить на оси абсцисс
интервал x > a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
t t1 2 n; t1 2 n ,
n Z
6. Неравенство cost ≤ a
t1-1
a
2π-t1
y
0
1
x
1. Отметить на оси абсцисс
интервал x ≤ a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
t t1 2 n; 2 t1 2 n ,
n Z
7. Неравенство sint > a
Неравенство sint > ay
1
π-t1
t1
a
0
x
1. Отметить на оси ординат
интервал y > a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
t t1 2 n; t1 2 n ,
-1
n Z
8. Неравенство sint ≤ a
y1
t1
3π-t1
a
0
x
1. Отметить на оси ординат
интервал y≤a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Записать числовые значения
граничных точек дуги.
4. Записать общее решение
неравенства.
t t1 2 n; 3 t1 2 n ,
-1
n Z
9. Решение простейших тригонометрических неравенств ПРИМЕРЫ
10.
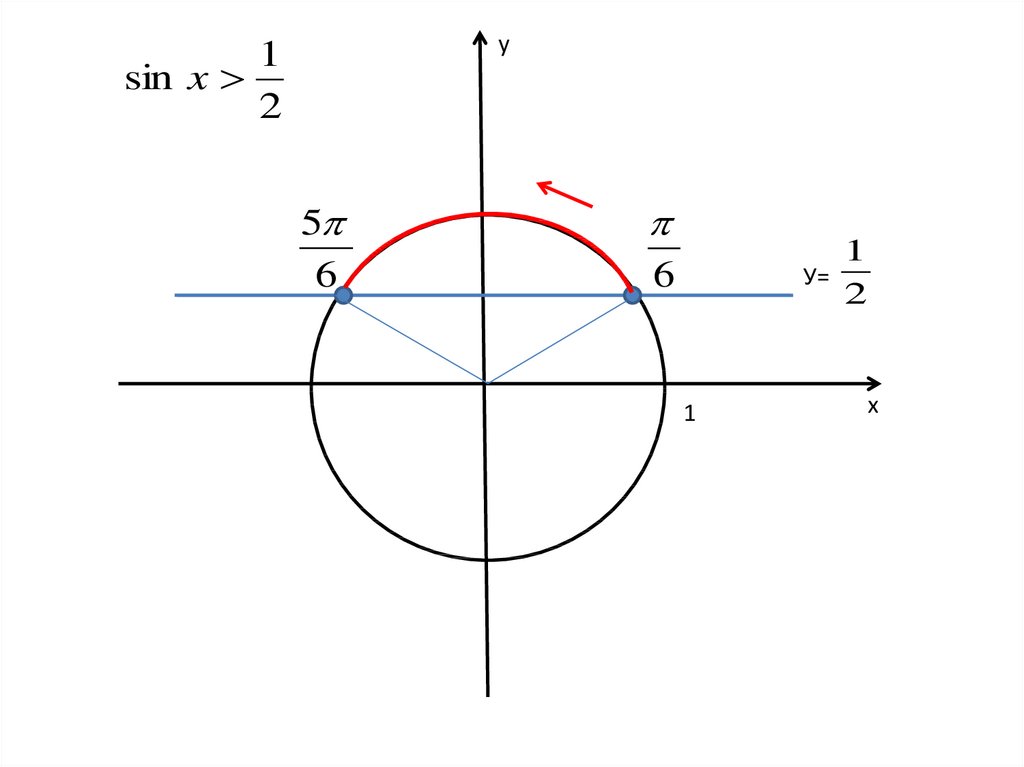
1sin x >
2
у
1
У=
2
1
х
11.
1sin x
2
у
1
У=
2
1
х
12.
у1
sin x
2
5
6
1
У=
2
6
1
х
13.
у1
sin x
2
5
6
1
У=
2
6
1
х
5
2 n x
2 n
6
6
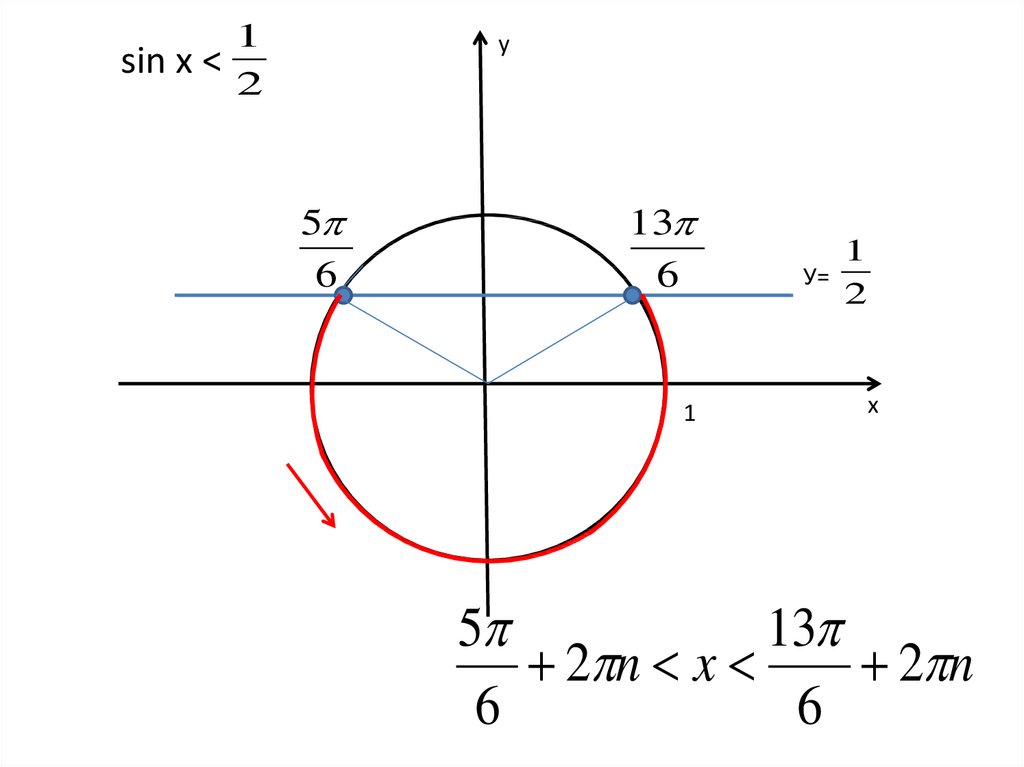
14.
1sin x <
2
у
5
6
13
6
1
1
У=
2
х
5
13
2 n x
2 n
6
6
15.
1х
2
у
1
cos x
2
1
х
16.
1х
2
у
1
cos x
2
1
х
17.
1х
2
у
1
cos x
2
2
3
1
2
3
х
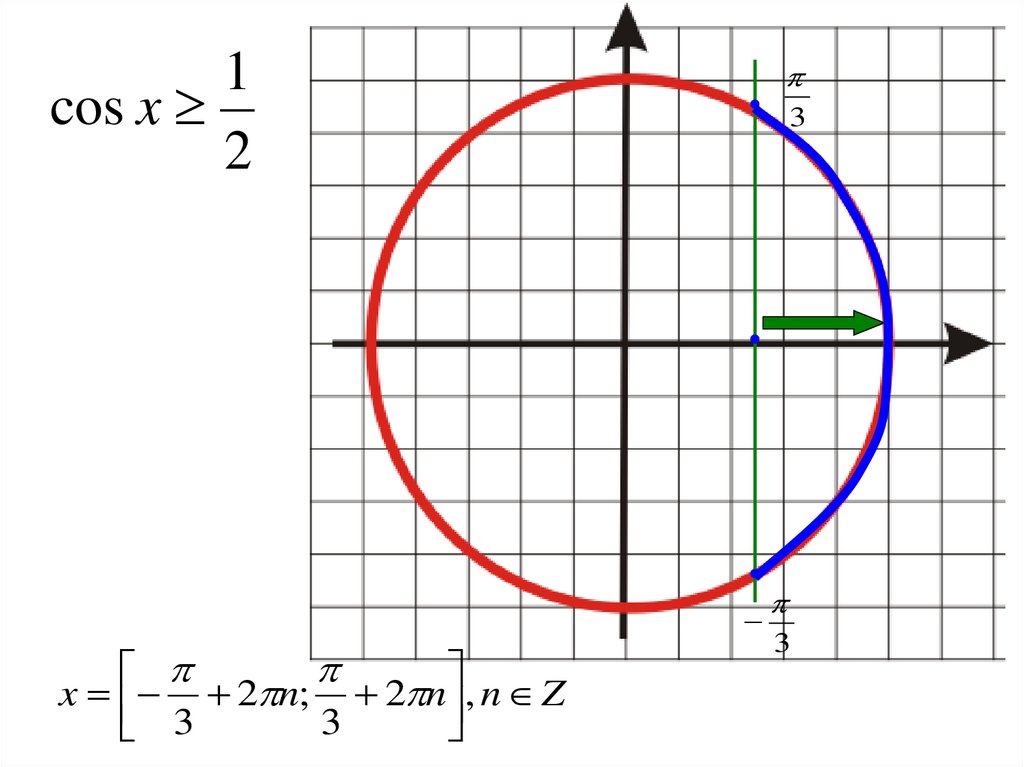
18.
1х
2
у
1
cos x
2
2
3
1
х
2
3
2
2
2 n x
2 n
3
3
19.
1х
2
у
1
cos x
2
2
3
1
х
4
3
2
4
2 n x 2 n
3
3
20. Тригонометрические неравенства
Решим неравенство:1
sin x
2
21.
1sin x
2
Решением уравнения
являются x =
6
2 n,
1
sin x
2
5
2 n
6
и
которые соответствуют точкам на единичной окружности
с ординатой, равной 0,5
1
sin x
2
Решением
неравенства
будут все точки единичной
числовой окружности,
у которых ордината
больше
5
6
1
2
5
x 2 n;
2 n , n Z
6
6
1
1
2
0
6
1
22.
1sin x
2
6
5
6
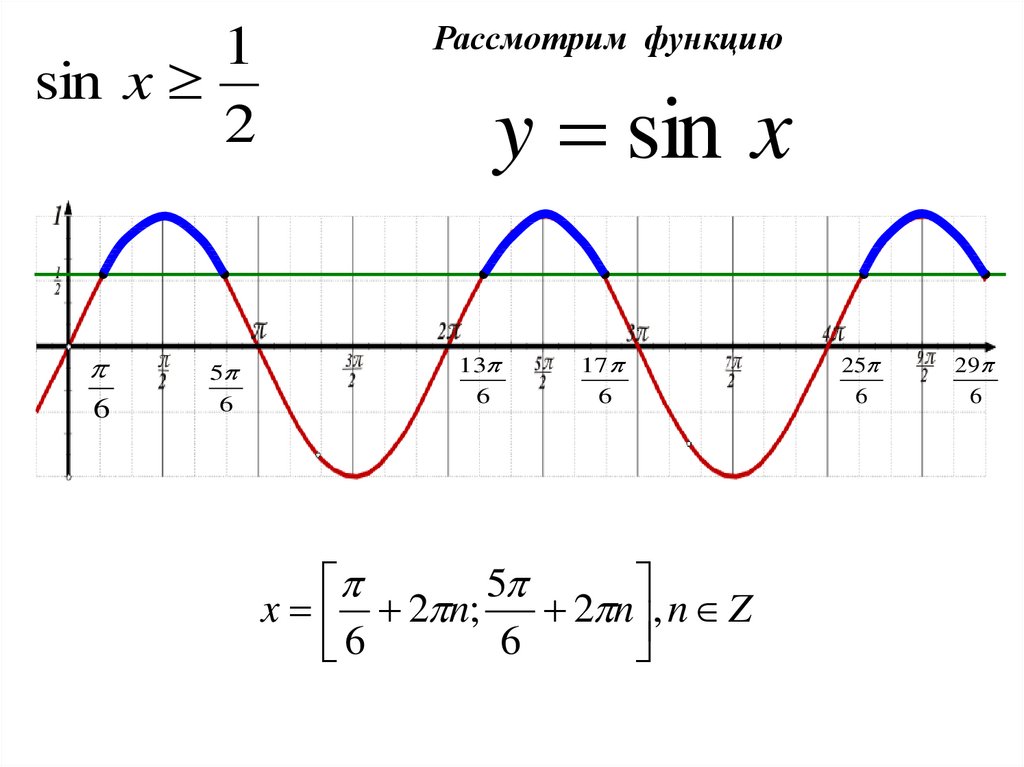
Рассмотрим функцию
y sin x
13
6
17
6
5
x 2 n;
2 n , n Z
6
6
25
6
29
6
23.
Рассмотрим неравенство :1
sin x
2
24.
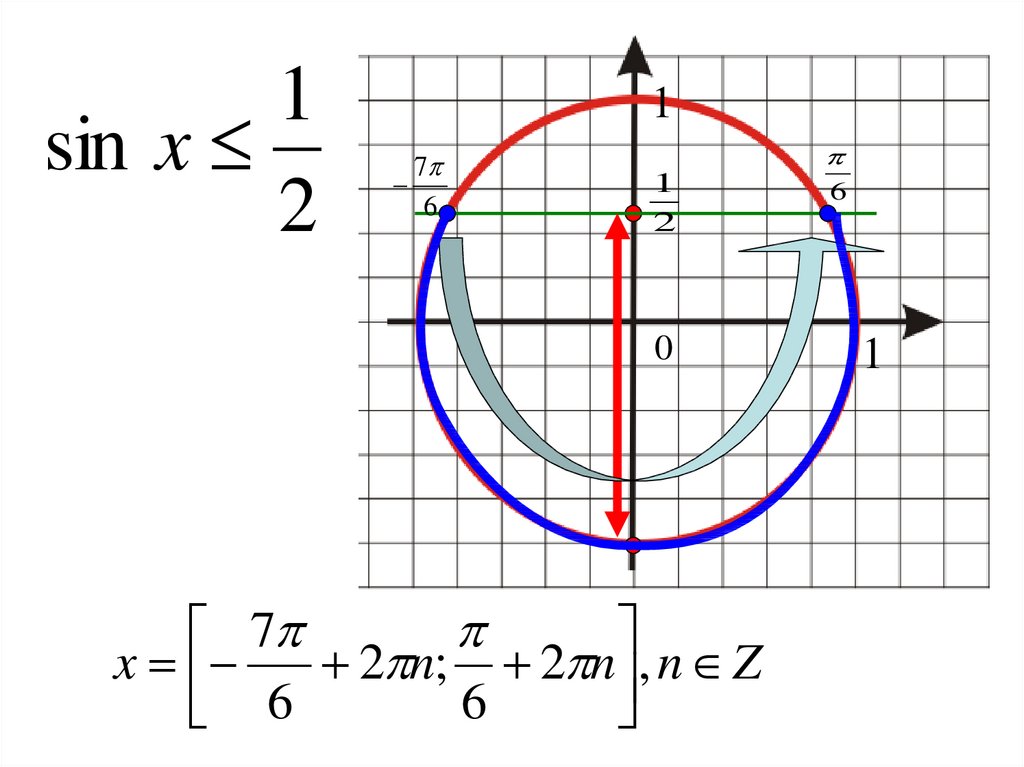
1sin x
2
1
7
6
1
2
0
7
x
2 n; 2 n , n Z
6
6
6
1
25.
1sin x
2
6
5
6
13
6
17
6
7
x
2 n; 2 n , n Z
6
6
25
6
29
6
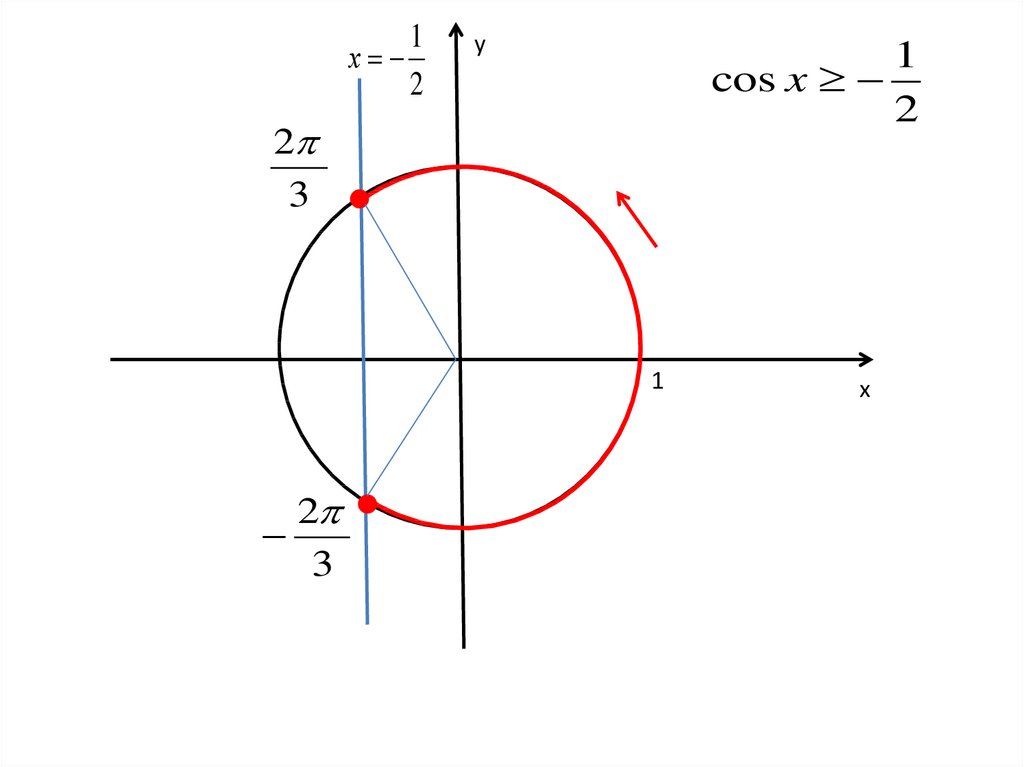
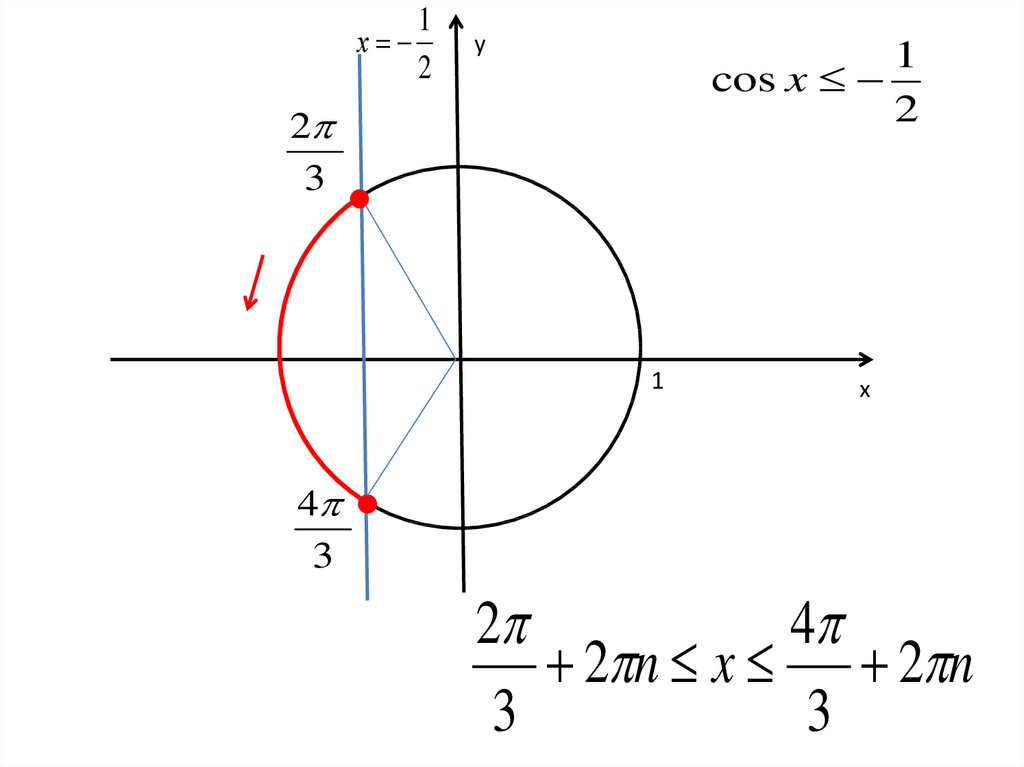
26.
1cos x
2
3
x 2 n; 2 n , n Z
3
3
3
27.
1cos x
2
3
5
x 2 n;
2 n , n Z
3
3
3
2
5
3
28.
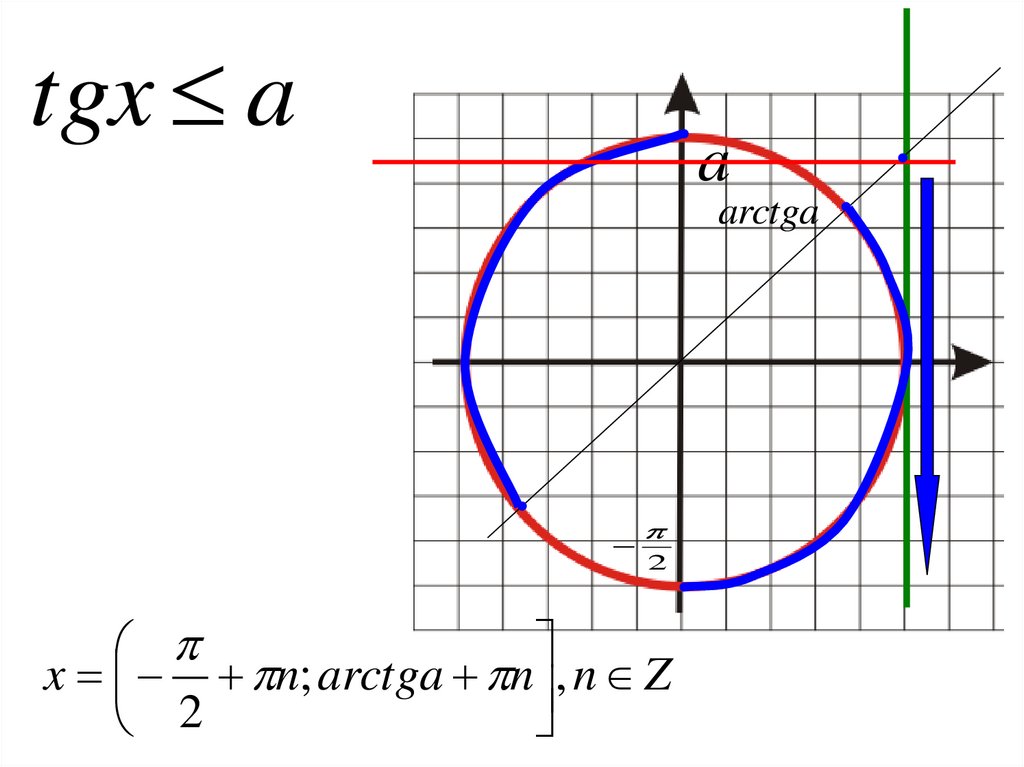
tgx aa
arctga
2
x n; arctga n , n Z
2
















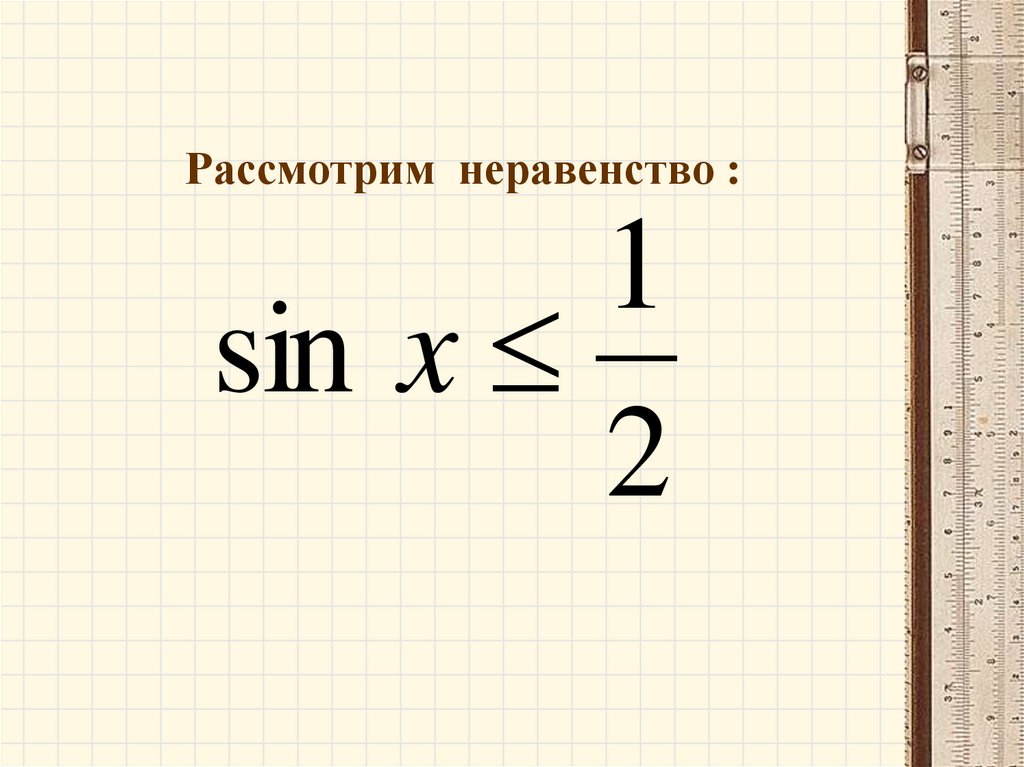


 mathematics
mathematics








