Similar presentations:
Решение простейших тригонометрических неравенств
1.
Решениепростейших тригонометрических
неравенств
2.
Математический диктант1 ВАРИАНТ.
Решите уравнение:
1
2
1
cos x
2
sin x 1
3
1
tgx
3
4
5
6
2 ВАРИАНТ.
Решите уравнение:
1
2
3
tgx 1
3
2
2
sin x
2
cos 2 x
cos 2 x
3
2
4
sin 3x
2
2
5
cos( x ) 1
6
6
1
sin( x) 1
2
tg ( x ) 3
6
tgx
1
3
3.
Все сложные тригонометрические неравенства решаютсяпростейшие
тригонометрические
решаются
сВсе
помощью
тех же
алгоритмов, что инеравенства
тригонометрические
одним
и темконце
же способом:
уравнения, но
в самом
приходится решать
простейшие тригонометрические неравенства.
1. Выделяем на единичной окружности дугу, координаты точек
которой удовлетворяют нашему неравенству.
2. Определяем начальную точку движения по этой дуге, исходя
из того, что мы «умеем» двигаться только в положительном
направлении, то есть против часовой стрелки (от меньшего
числа к большему)
3. Двигаясь по выделенной дуге в положительном направлении,
определяем конечную точку движения.
4. После того, как мы определили начальную и конечную точку
движения по дуге, записываем решение неравенства и ответ.
4.
̶—4π
3 2π
—
̶—
5π 3π 3
4 —
4
̶—
7π 5π
—
6 6
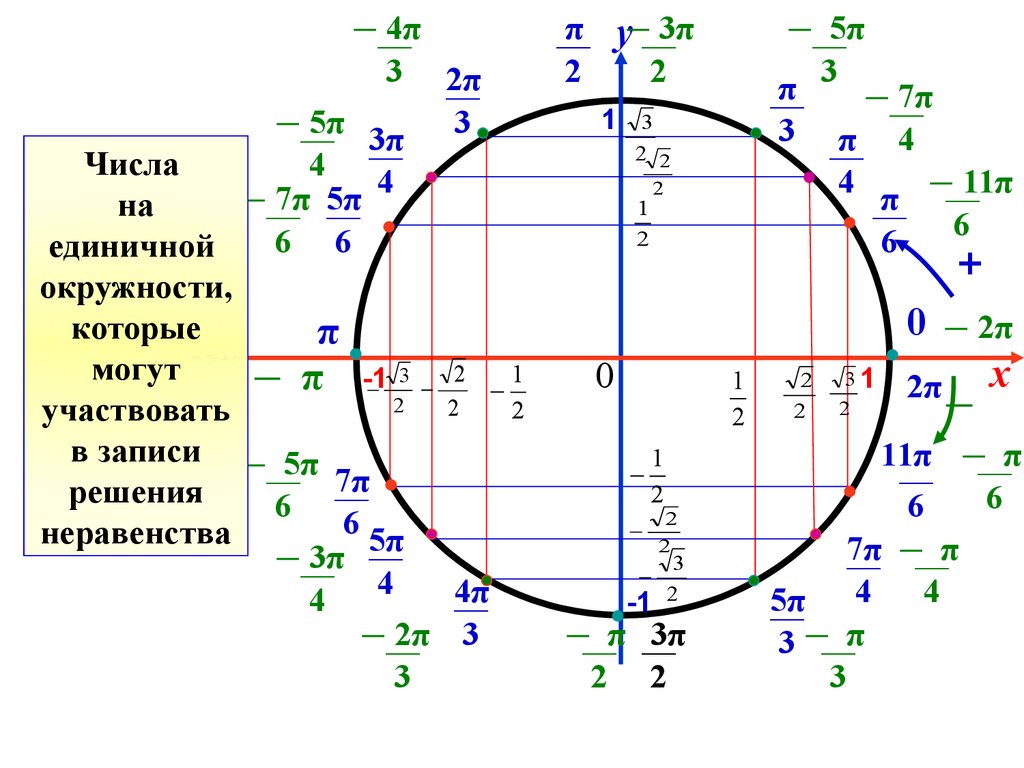
Числа
на
единичной
окружности,
которые
π
могут
2
3
1
̶ π -1
2
2
2
участвовать
в записи
̶—5π 7π
решения
6 —
6 5π
неравенства
̶—
3π —
4
4π
4
—
̶—
2π 3
3
π y—
̶ 3π
—
2
2
1
̶—5π
3
π
̶—
7π
—
3 π 4
—
4 π —
̶ 11π
— 6
6
3
2 2
2
1
2
+
0
1
2
1
2
-1
2
2
3
2
̶ π —
3π
—
2 2
2
2
31
2
0
̶ 2π
2π
x
̶
11π —
̶ π
—
6
6
7π
̶ π
— —
4 4
5π
— ̶ π
3 —
3
5.
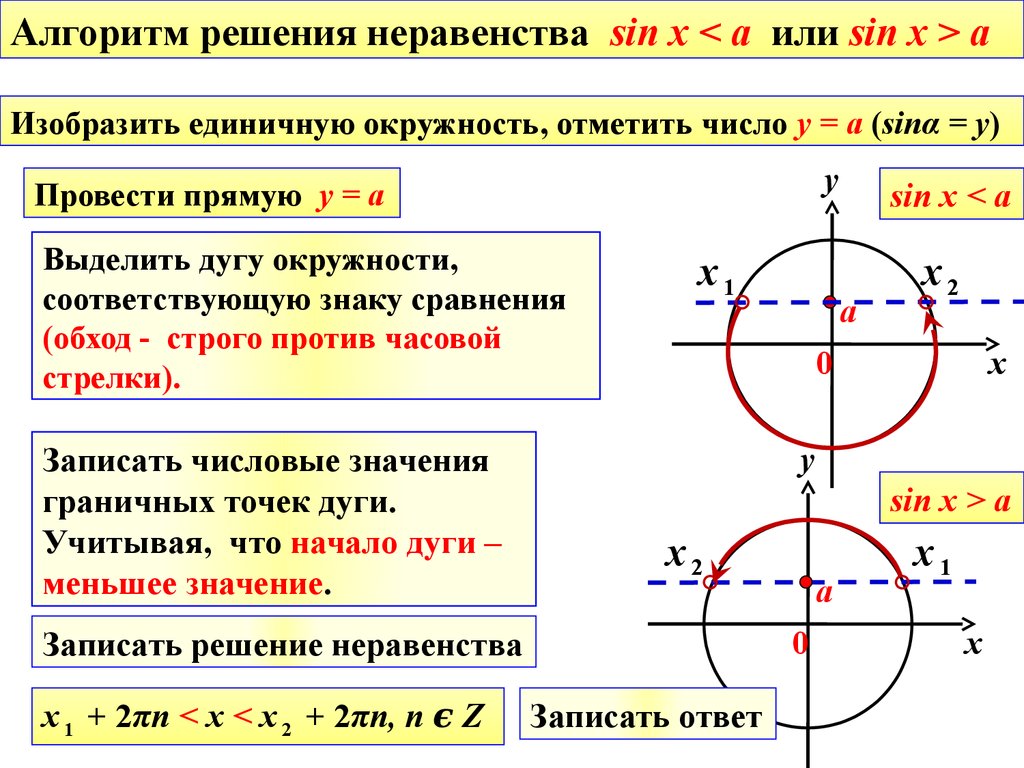
Алгоритм решения неравенства sin x < a или sin x > aИзобразить единичную окружность, отметить число у = a (sinα = y)
y
Провести прямую у = a
Выделить дугу окружности,
соответствующую знаку сравнения
(обход - строго против часовой
стрелки).
Записать числовые значения
граничных точек дуги.
Учитывая, что начало дуги –
меньшее значение.
х1
a
х2
0
х
y
sin x > a
х2
a
0
Записать решение неравенства
х 1 + 2πn < x < х 2 + 2πn, n ϵ Z
sin x < a
Записать ответ
х1
х
6.
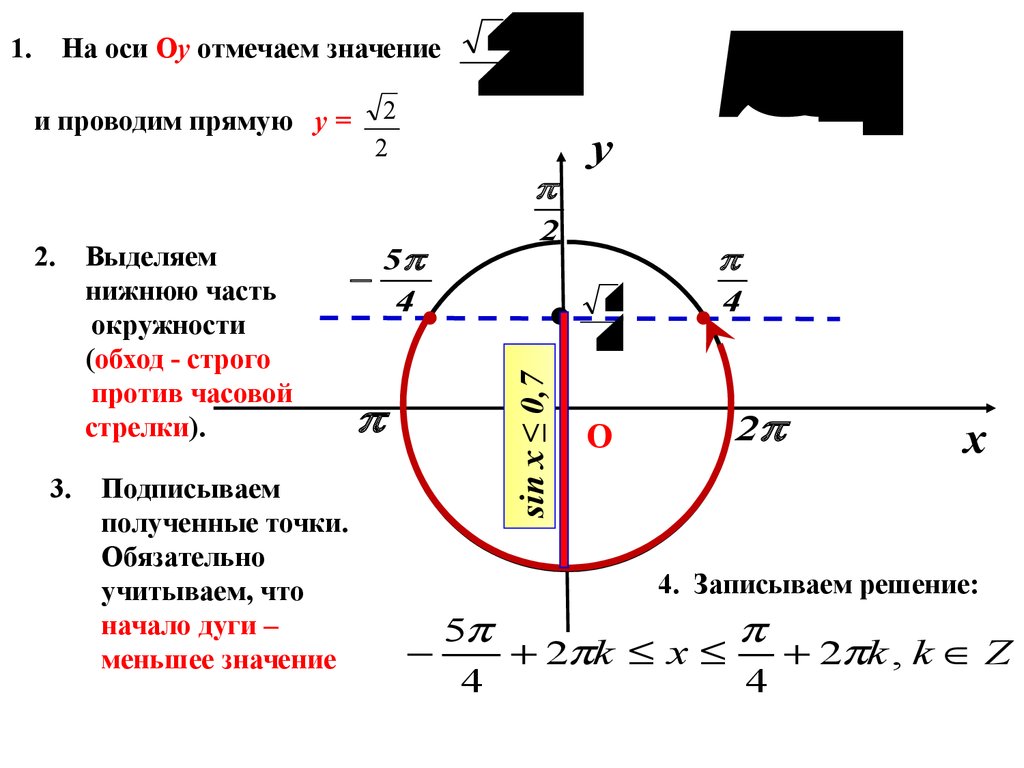
1.На оси Оу отмечаем значение
2
2
и проводим прямую у =
2
0,72sin
2
x
3.
Выделяем
нижнюю часть
окружности
(обход - строго
против часовой
стрелки).
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение
5
4
2
4
sin x ≤ 0,7
2.
y
О
2
x
4. Записываем решение:
5
2 k x
2 k , k Z
4
4
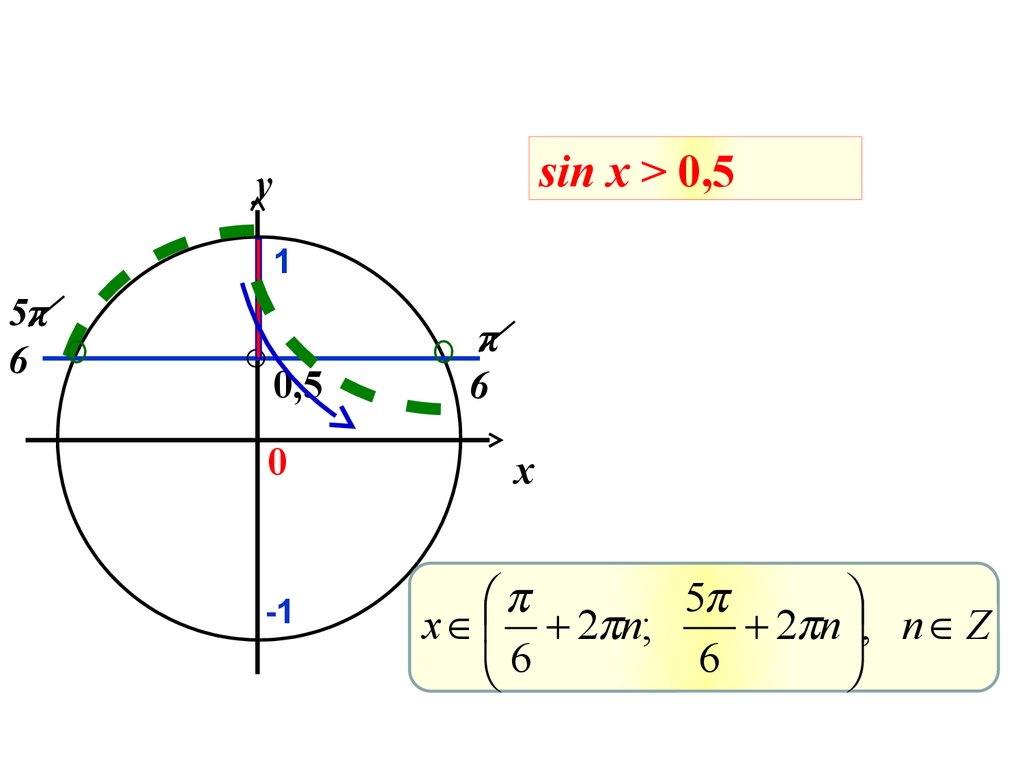
7. sin x > 0,5
sin x > 0,5y
1
5π
6
0,5
0
-1
π
6
x
5
x 2 n;
2 n , n Z
6
6
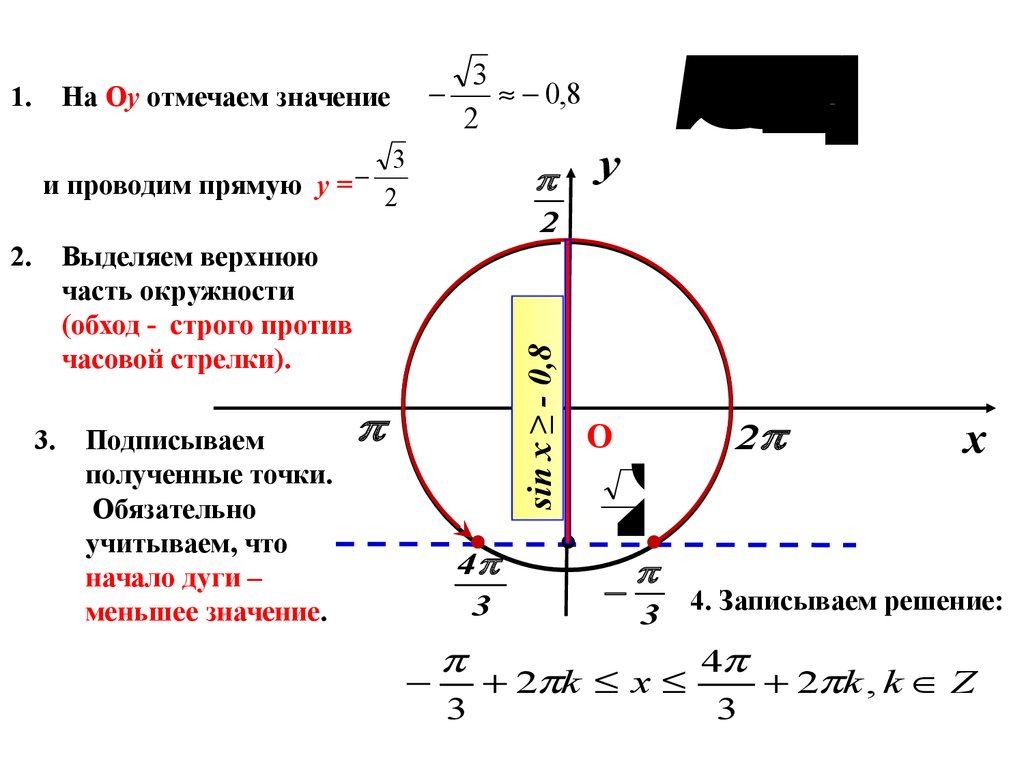
8.
1.На Оу отмечаем значение
3
и проводим прямую у = 2
2
Выделяем верхнюю
часть окружности
(обход - строго против
часовой стрелки).
3.
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение.
sin x ≥ - 0,8
2.
3
s 23in
x 2
3
0,8
2
4
3
3
y
2
О
x
3 4. Записываем решение:
2 k x
4
2 k , k Z
3
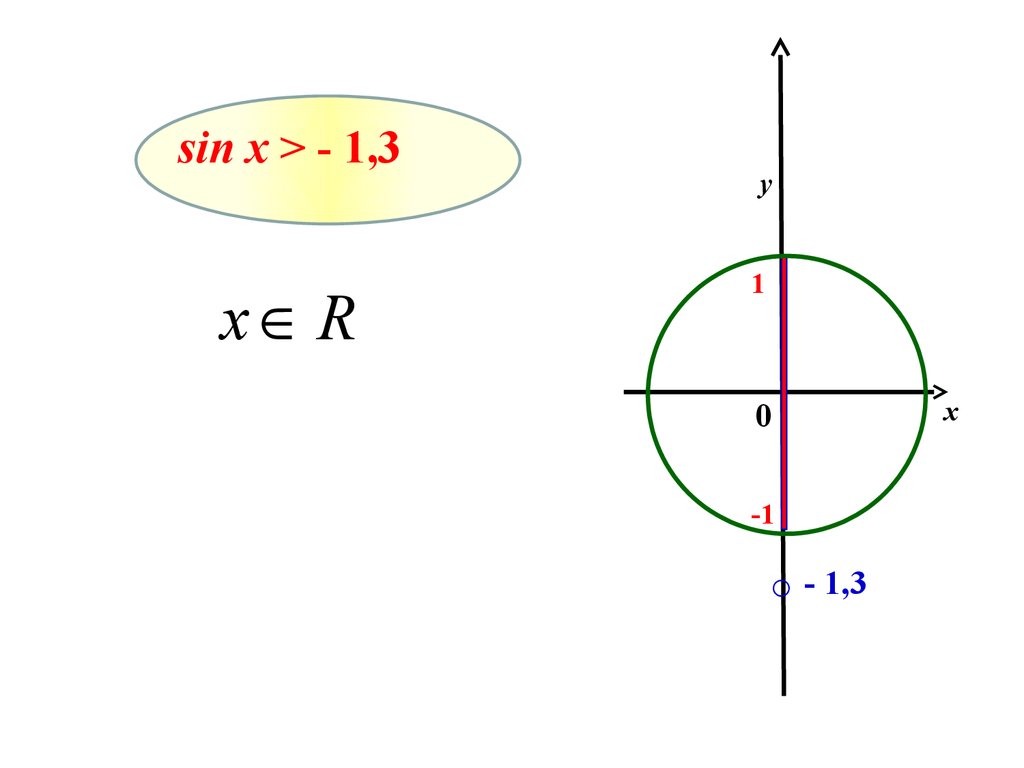
9.
sin x > - 1,3x R
y
1
0
-1
○ - 1,3
x
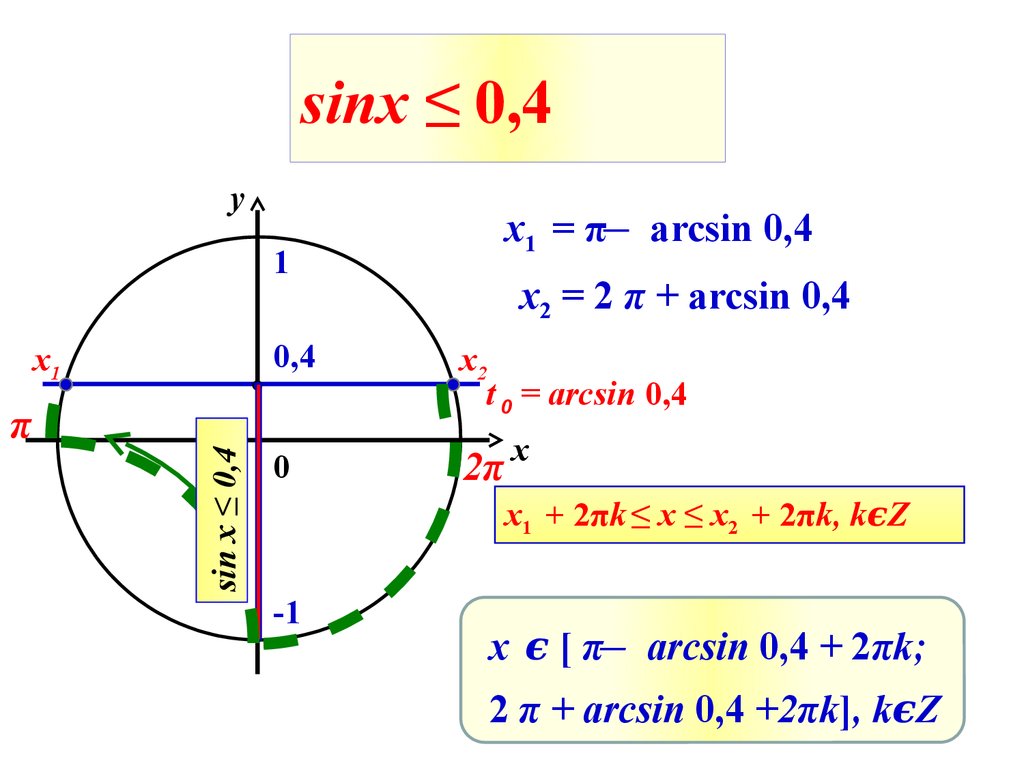
10. sinx ≤ 0,4
y1
x1
x2 = 2 π + arcsin 0,4
0,4
x2
t 0 = arcsin 0,4
0
2π x
π
sin x ≤ 0,4
x1 = π ̶ arcsin 0,4
x1 + 2πk ≤ x ≤ x2 + 2πk, kϵZ
-1
x ϵ[π
arcsin 0,4 + 2πk;
2 π + arcsin 0,4 +2πk], kϵZ
11.
Задача.Имеется закон изменения силы
переменного тока:
Вопрос.
Найти в какой момент времени сила тока
больше
.
12.
Решим неравенство1
sin( 2 t 3 )
2
1
2 t 3 x
получим sin x
Обозначим
2
5
x0 , x1 ,
6
6
6
5
2 k x 2 k ,k Z
6
6
5
2 k 2 t 3 2 k ,k Z
6
6
5
3 2 k 2 t 3 2 k ,k Z
6
6
17
13
2 k 2 t
2 k ,k Z
6
6
17
13
17
13
t ( k ; k ,k Z )
k t k ,k Z
12
6
12
6
5
5sin( 2 t 3 )
2
13.
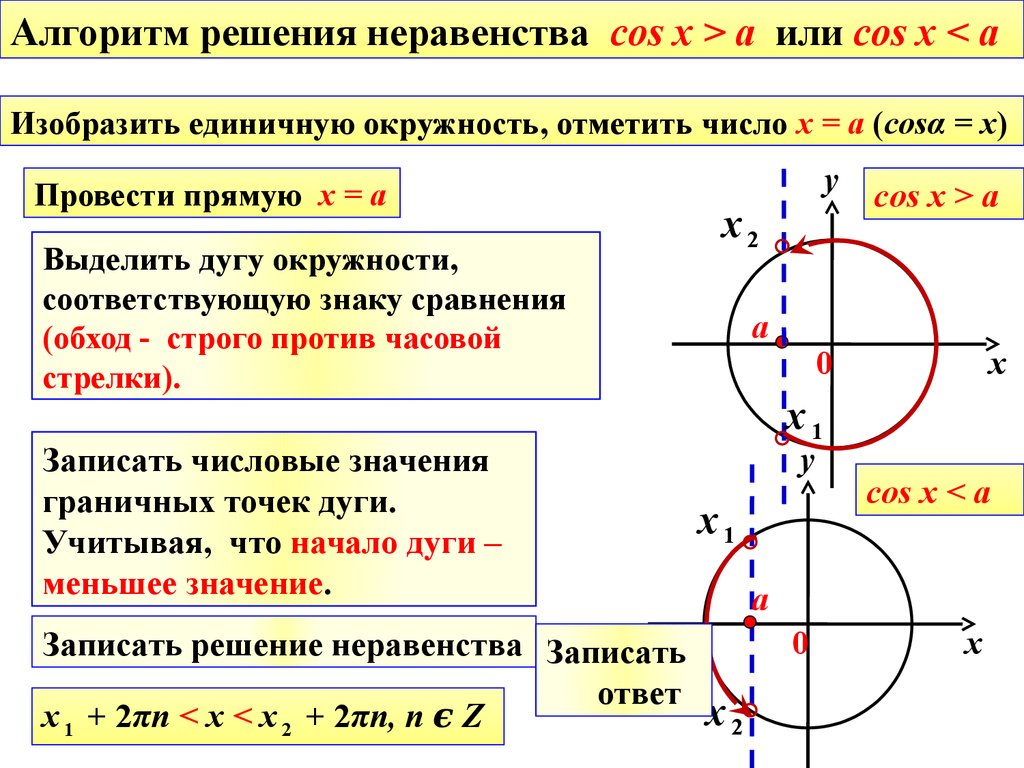
Алгоритм решения неравенства cos x > a или cos x < aИзобразить единичную окружность, отметить число x = a (cosα = x)
Провести прямую x = a
Выделить дугу окружности,
соответствующую знаку сравнения
(обход - строго против часовой
стрелки).
Записать числовые значения
граничных точек дуги.
Учитывая, что начало дуги –
меньшее значение.
y
cos x > a
0
х
х2
a
х1
y
х1
Записать решение неравенства Записать
ответ
х2
х 1 + 2πn < x < х 2 + 2πn, n ϵ Z
cos x < a
a
0
х
14.
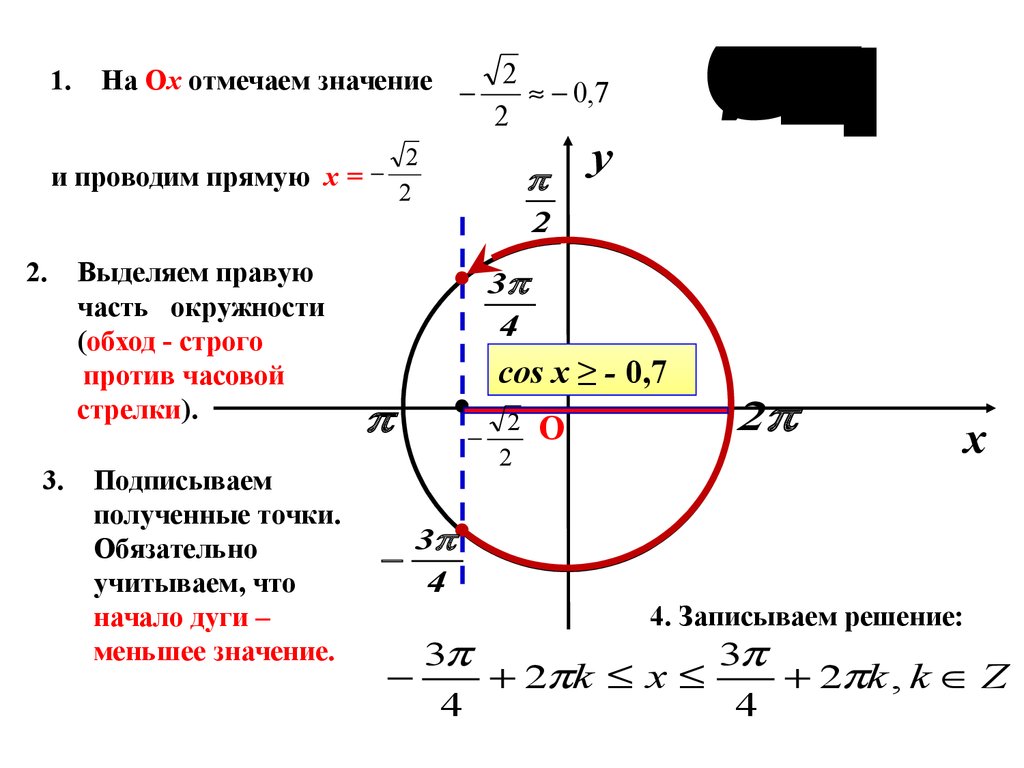
1.На Ох отмечаем значение 2 0,7
2
2
2
и проводим прямую х =
2.
3.
Выделяем правую
часть окружности
(обход - строго
против часовой
стрелки).
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение.
y
2
3
4
cos x ≥ - 0,7
2
2
О
2
cosx
2
x
3
4
4. Записываем решение:
3
3
2 k x
2 k , k Z
4
4
15.
1.1
1
c
o
s
x
2
22
1
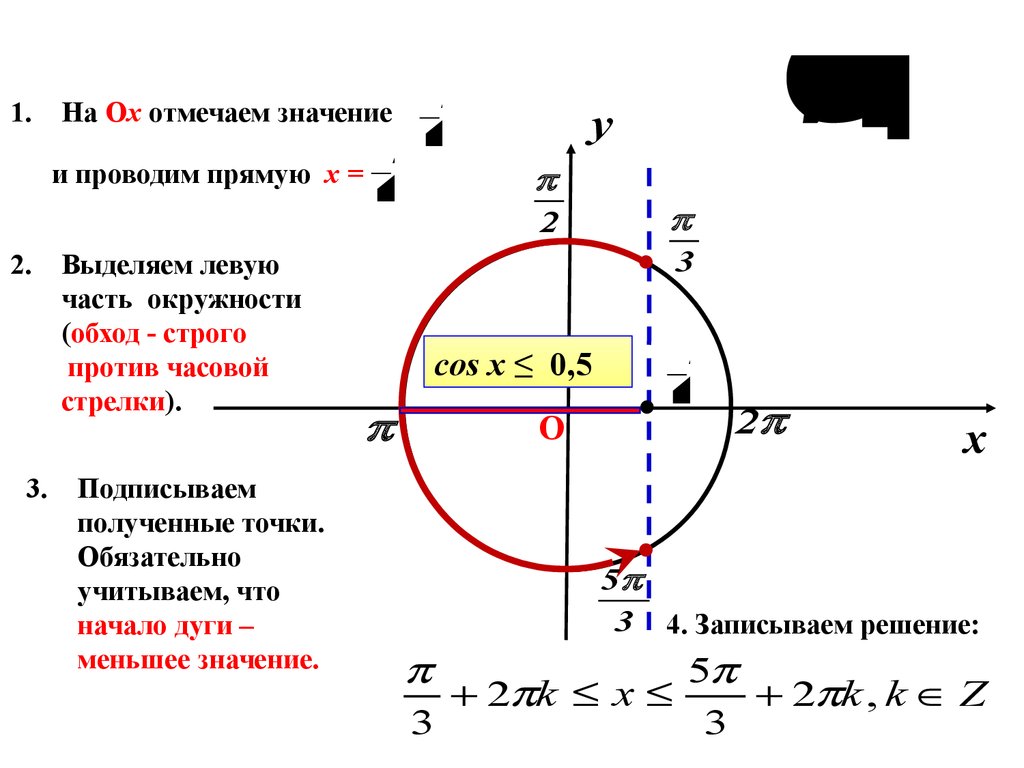
На Оx отмечаем значение
и проводим прямую х =
y
2
2.
3.
Выделяем левую
часть окружности
(обход - строго
против часовой
стрелки).
Подписываем
полученные точки.
Обязательно
учитываем, что
начало дуги –
меньшее значение.
3
cos x ≤ 0,5
О
2
x
5
3 4. Записываем решение:
5
2 k x
2 k , k Z
3
3
16.
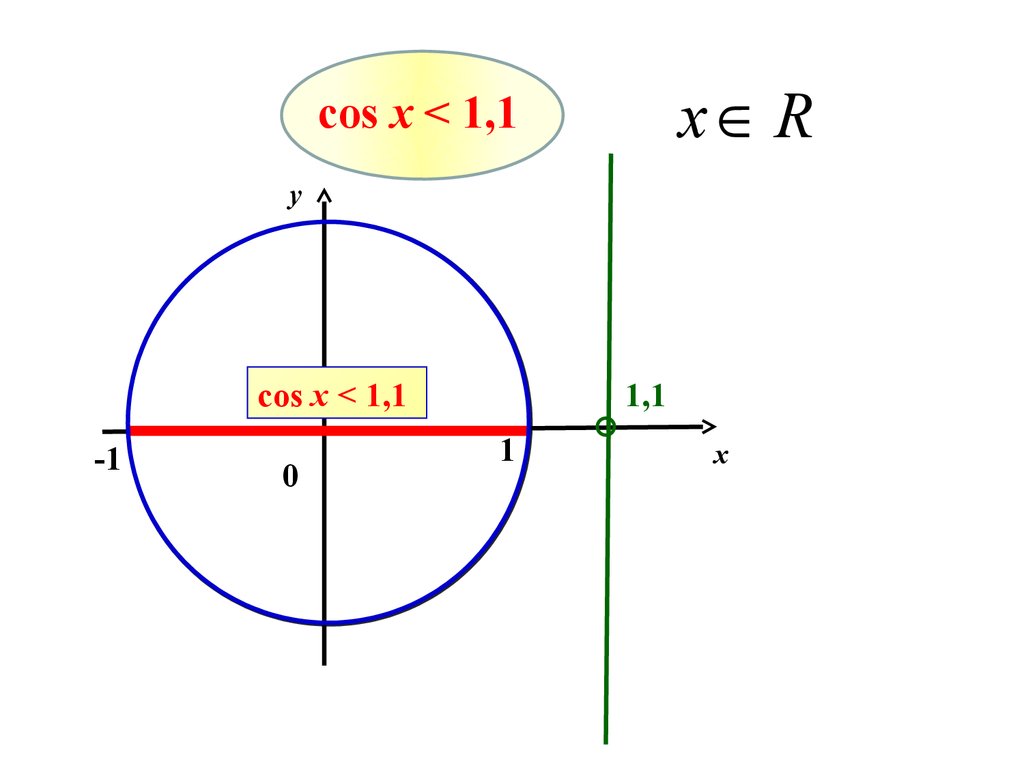
x Rcos х < 1,1
y
cos х < 1,1
-1
0
1,1
1
x
17.
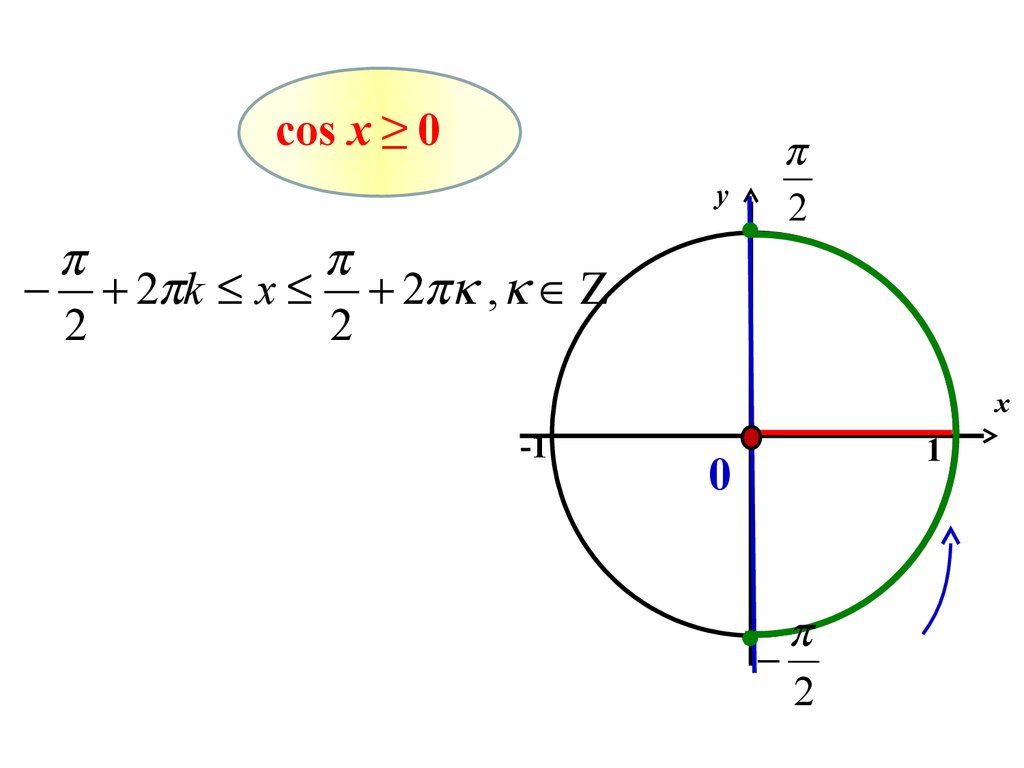
cos x ≥ 0y
2 k x 2 ,
2
2
2
x
-1
1
0
2
18. РЕШИ САМОСТОЯТЕЛЬНО:
11) cos x ;
2
3
2) cos( x )
;
3
2
3) cos( 2 x ) 0.
4
19. ПРОВЕРЬ СВОЙ ОТВЕТ:
51) 2 n x
2 n, n ;
3
3
7
2)
2 n x 2 n, n ;
6
2
3
7
3)
n x
n, n .
8
8
20.
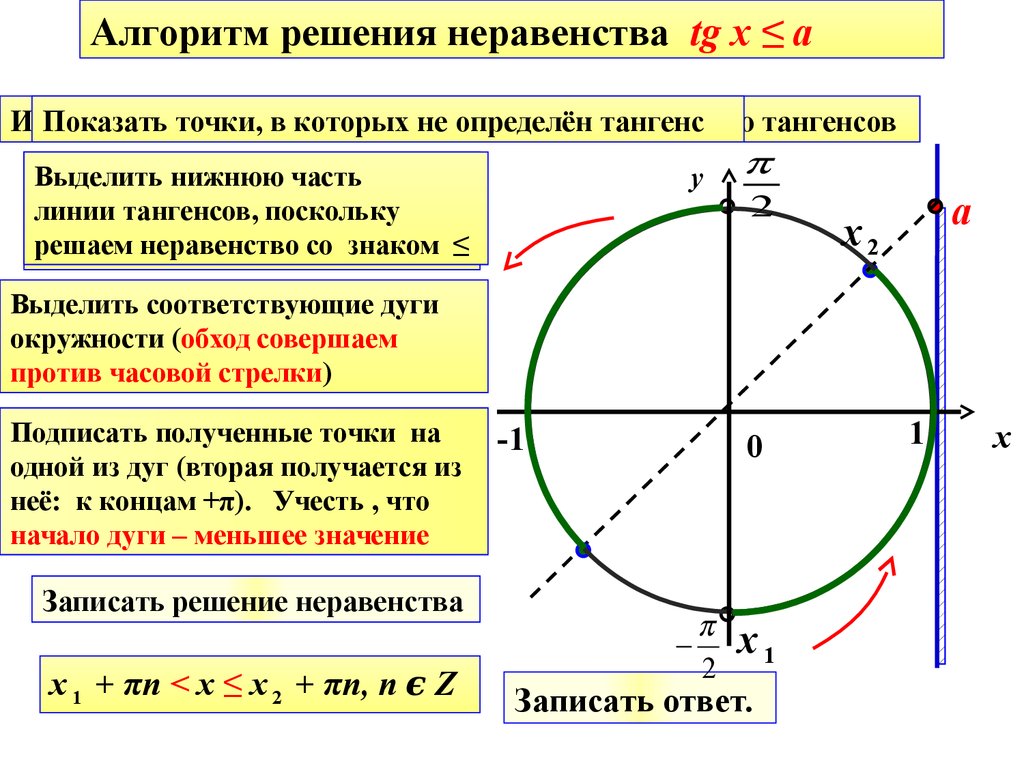
Алгоритм решения неравенства tg x ≤ aИзобразить
Показать единичную
точки, в которых
окружность
не определён
и провести
тангенс
линию тангенсов
Выделить
часть
На
линии нижнюю
тангенсов
отметить
линии
поскольку
число тангенсов,
a и провести
луч через
решаем
неравенство
со знаком ≤
эту точку
и центр окружности
y
2
а
х2
Выделить соответствующие дуги
окружности (обход совершаем
против часовой стрелки)
Подписать полученные точки на
одной из дуг (вторая получается из
неё: к концам +π). Учесть , что
начало дуги – меньшее значение
Записать решение неравенства
х 1 + πn < x ≤ х 2 + πn, n ϵ Z
-1
0
2
х1
Записать ответ.
1
x
21.
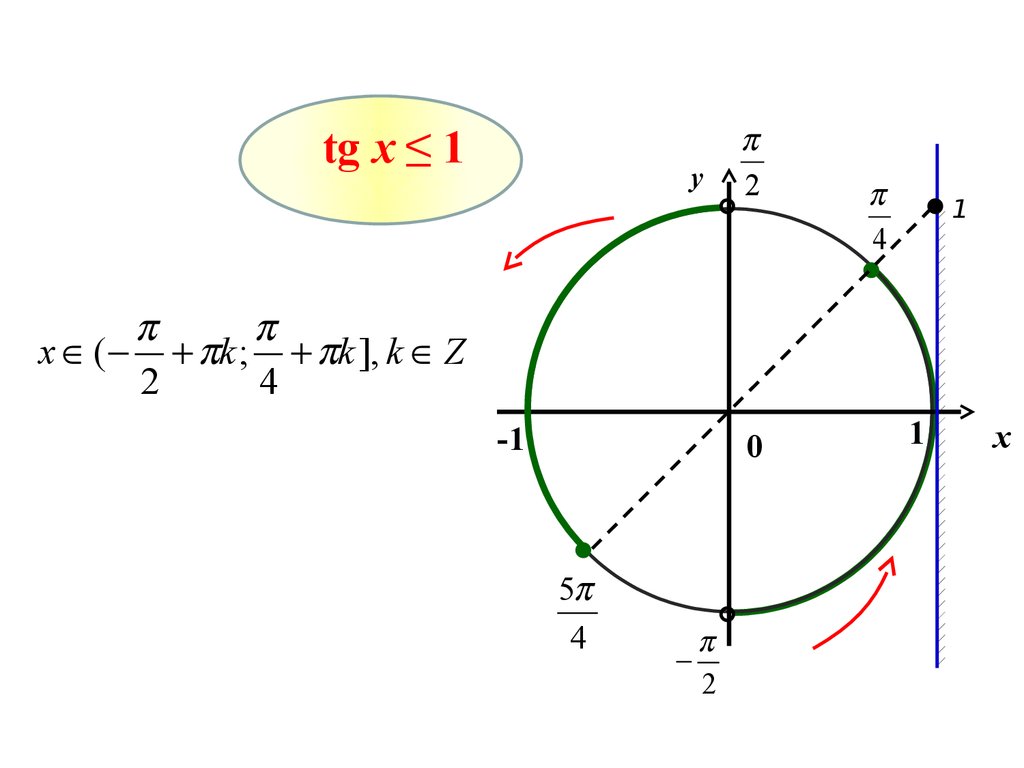
tg x ≤ 1y
2
4
1
x ( k ; k ], k Z
2
4
-1
0
5
4
2
1
x
22.
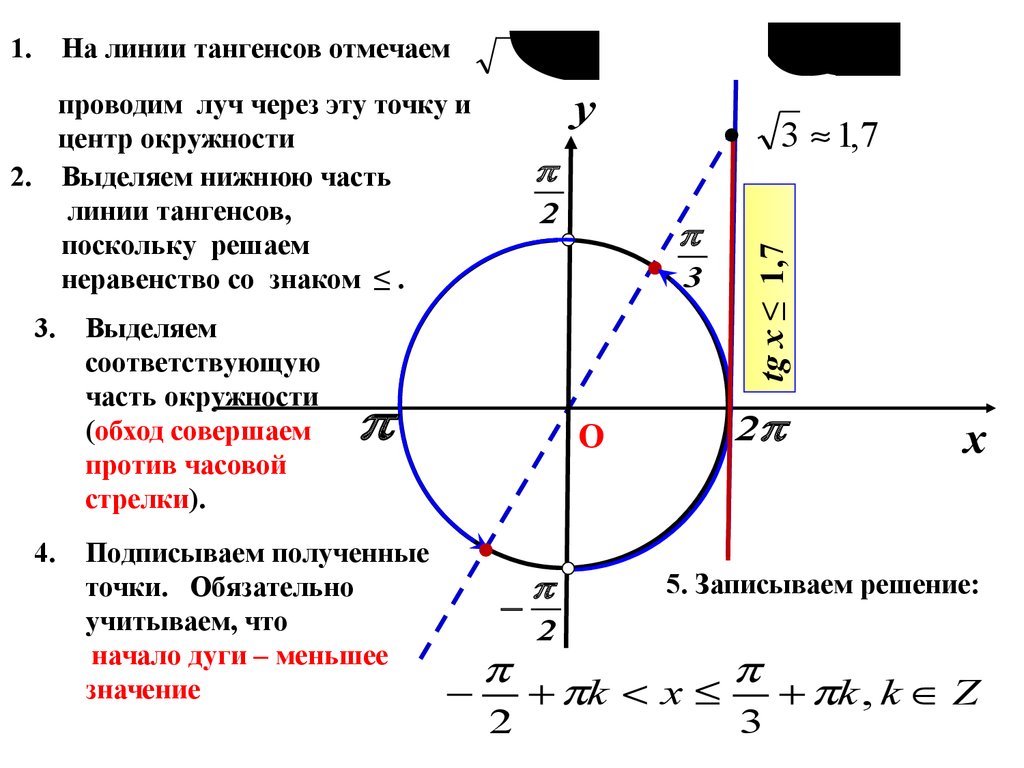
На линии тангенсов отмечаемпроводим луч через эту точку и
центр окружности
2. Выделяем нижнюю часть
линии тангенсов,
поскольку решаем
неравенство со знаком ≤ .
3.
4.
Выделяем
соответствующую
часть окружности
(обход совершаем
против часовой
стрелки).
3 1,7tgx 3
y
2
3
Подписываем полученные
точки. Обязательно
учитываем, что
начало дуги – меньшее
значение
3 1,7
2
О
2
tg x ≤ 1,7
1.
x
5. Записываем решение:
2
k x
3
k , k Z
23.
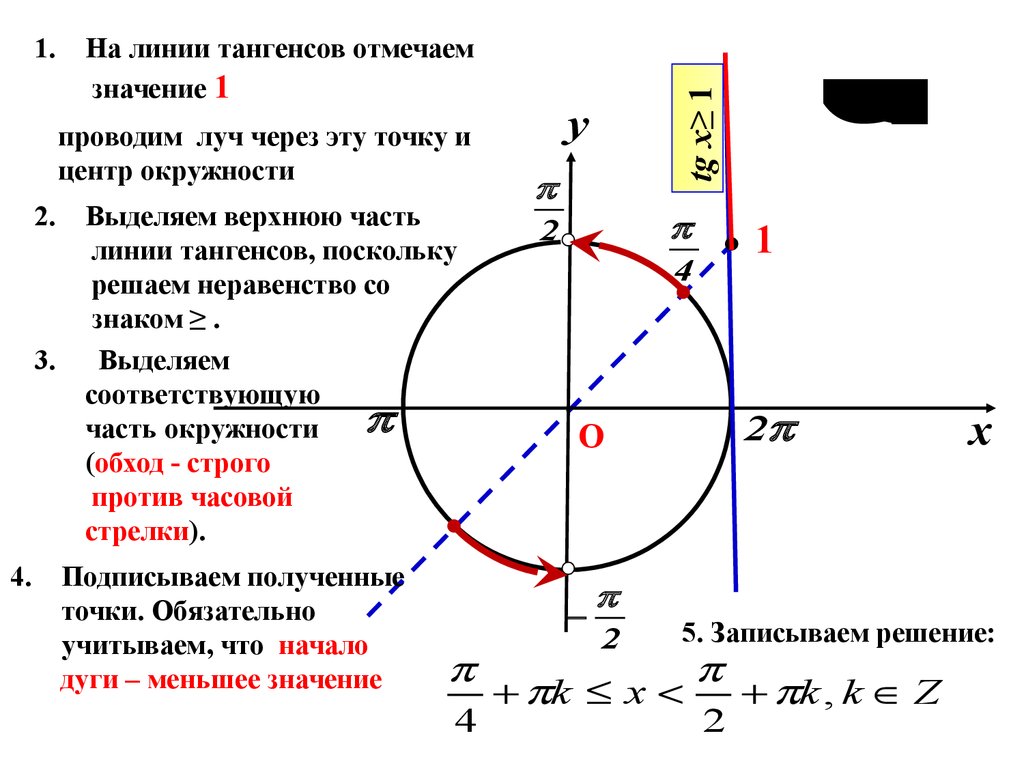
На линии тангенсов отмечаемзначение 1
проводим луч через эту точку и
центр окружности
2.
3.
4.
Выделяем верхнюю часть
линии тангенсов, поскольку
решаем неравенство со
знаком ≥ .
Выделяем
соответствующую
часть окружности
(обход - строго
против часовой
стрелки).
Подписываем полученные
точки. Обязательно
учитываем, что начало
дуги – меньшее значение
y
2
4
1
4
tgx 1
2
О
tg x≥ 1
1.
x
2
5. Записываем решение:
k x
2
k , k Z
24.
25.
26. Математический диктант №5 по теме «Простейшие тригонометрические уравнения»
Математический диктант №5 по теме«Простейшие тригонометрические уравнения»
1 вариант
1
2
2 вариант
Найдите корень уравнения
(8x 1)
3
cos
6
2
В ответе запишите наибольший
отрицательный корень.
( x 5)
Найдите корень уравнения.
tg
3
3
В ответе запишите наименьший
положительный корень.
Найдите корень уравнения
1
2
Найдите корень уравнения
( x 9)
2
sin
3
4
2
В ответе запишите наименьший
положительный корень.
Найдите корень уравнения
cos
4
положительный корень.
Найдите корень уравнения
(4 x 3)
sin
1
4
В ответе запишите наибольший
отрицательный корень.
Найдите корень уравнения
(4 x 1)
cos
3
8 x
1
6
В ответе запишите наибольший
отрицательный корень.
( x 6) 1
6
3
В ответе запишите наименьший
tg
6
В ответе запишите наибольший
отрицательный корень.
Найдите корень уравнения.
2 x
sin
4
1
2
3
1
2
В ответе запишите наименьший
положительный корень.










 mathematics
mathematics








