Similar presentations:
Понятие матрица
1. Понятие матрица
2. Определение. Таблица, составленная из m×n чисел называется матрицей размерности m×n,
а11а21
...
a
m1
а12
а22
...
am 2
... а1n
... а2 n
A aij
... ...
... amn
m – число строк, n – число столбцов.
m x n – размер матрицы.
Числа аij называются элементами матрицы, i- номер
строки, j – номер столбца, на пересечении которых
стоит элемент.
3. Виды матриц
Опр: Две матрицы, имеющие одинаковую размерность m×n,называются матрицами одного типа
1. Если m≠n, то матрица называется прямоугольной.
1 2 3
А
4 0 2
2. Если m=n, то матрица называется квадратной n-го
порядка.
2 1
В
4 5
4.
А). Квадратная матрица называется диагональной, если все ееэлементы, кроме элементов главной диагонали, равны нулю
.
1 0 0
С 0 7 0
0 0 5
Б) Квадратная матрица называется единичной, если
элементы диагональной матрицы, стоящие на главной
диагонали равны единице.
1 0 0
Е 0 1 0
0 0 1
В) Квадратная матрица называется треугольной, если все
элементы матриц, расположенные выше или ниже главной
диагонали равны нулю.
1 4 7
0 3 5
0 0 5
или
1 0 0
4 4 0
6 5 9
5.
3. Матрица называется матрицей - строкой, если m=1D 1 0 2 5
4. Матрица называется матрицей - столбцом, если n=1
1
C 2
4
5. Матрица, все элементы которой равны нулю, называется
нулевой матрицей.
6.
• Равенство матриц. Две матрицы Аm×n и Bm×nодинаковой размерности равны, если равны
соответствующие элементы этих матриц.
Аm×n = Bm×n аij = bij
7.
Линейные операции над матрицами.,
Линейные операции – это сложение, вычитание, умножение
на число.
•Сложение и вычитание матриц.
Складывать и вычитать можно только матрицы
одинакового размера.
Чтобы сложить (или вычесть) две матрицы надо
сложить (вычесть) попарно их соответствующие
элементы.
а11 ...
А ... ...
a k1 ...
a1n
...
akn
b11 ... b1n
В ... ... ...
...
bkn
bk 1
а b
11 11
...
a b
k1
k1
... a1n b1n
...
...
... akn bkn
8.
:1 2 3 0 4 2 1 2 1
4
2
5
6
1 2 1 5 4
Задание: Сложите и вычтите матрицы
1 6 4
4 5 2
и В
А
0 3 2
1 2 1
9.
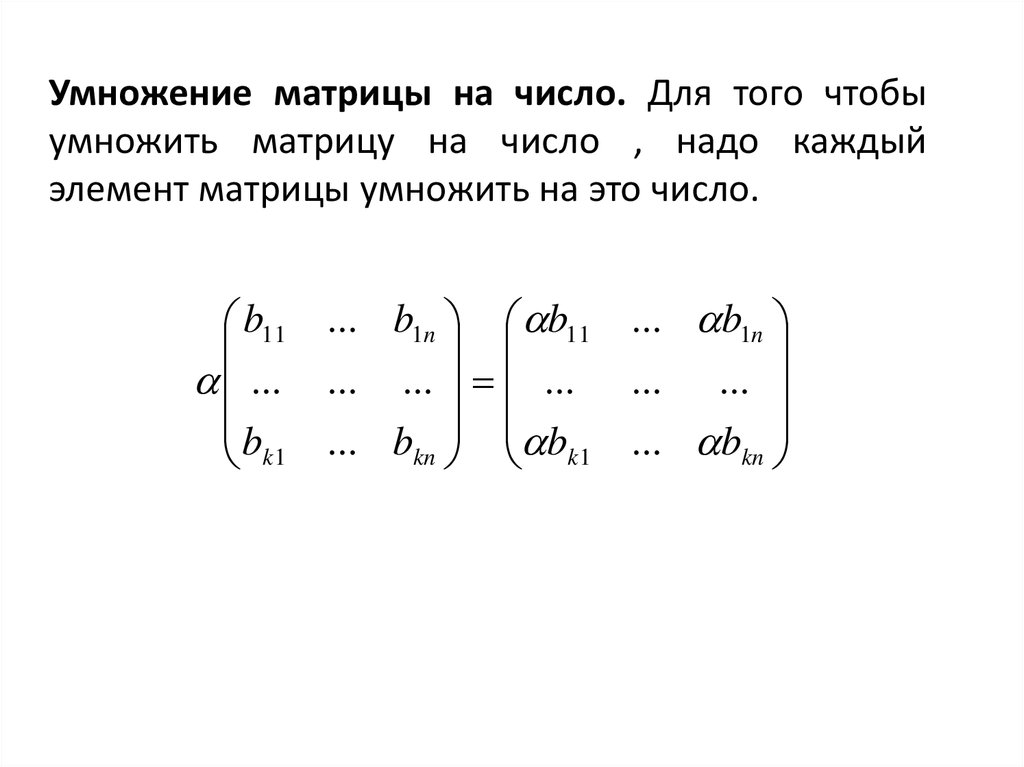
Умножение матрицы на число. Для того чтобыумножить матрицу на число , надо каждый
элемент матрицы умножить на это число.
b11 ... b1n b11 ... b1n
... ... ... ... ... ...
b
b
...
b
...
b
kn
kn
k1
k1
10.
2 1 3 2 3 1 6 33
5 0 3 5 3 0 15 0
1 6 4
4 24 16
, 4А
А
0 3 2
0 12 8
11.
Линейные операции над матрицами обладаютсвойствами, схожими со свойствами арифметических
операций над действительными числами:
СВОЙСТВА
A+B= B+A
(A+B) +C=A+(B+C)
A B A B
A A A
A A
свойства выполнимы для любых матриц А, В, С и
любых действительных чисел ,
12.
Транспонирование матриц.Операция транспонирования меняет местами строки и
столбцы, превращая матрицы размера (kxn) в матрицы
(nxk).
Обозначается символом Ат.
Замечание: (Ат)т=А.
T
1 2 1 3
3
4
2
4
1 2
1 1 0
1
3
2
3
1
0
1
T
1
2 3
T
1
2
3
13.
Умножение двух матриц.Чтобы умножить две матрицы, нужно все
элементы i-ой строки левой матрицы попарно
перемножить с соответствующими элементами
j-го столбца правой матрицы, все произведения
сложить и полученную сумму записать в новую
матрицу на место элемента, стоящего на
пересечении i-ой строки и j-го столбца.
По правилу «Строка на столбец».
14.
Замечание 1. Из этого определения следует,что умножать можно матрицы, у которых число
столбцов левой матрицы [m×s] равно числу
строк правой матрицы [s ×n]. В результате
получается матрица размерности m×n.
Замечание 2. Не для всех матриц
выполняется свойство, в основном АВ≠ВА .
Матрицы, для которых выполняется свойство
АВ=ВА называются коммутативными.








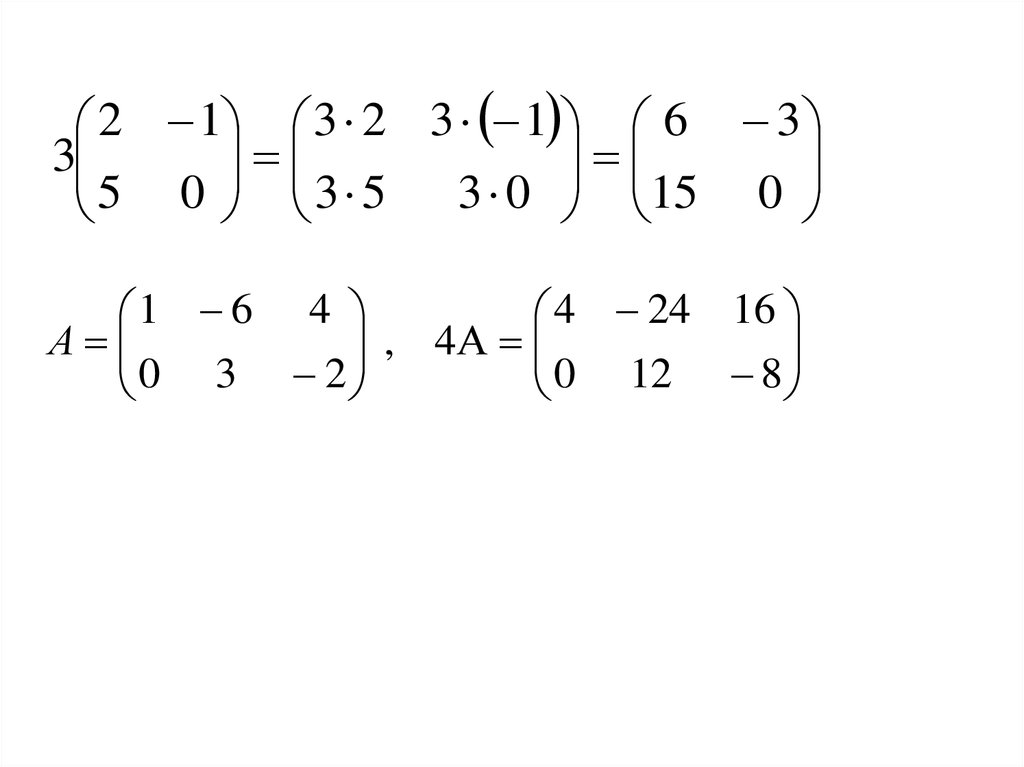






 mathematics
mathematics








