Similar presentations:
Введение в эконометрику. Корреляционный анализ. Практика-1
1.
Эконометрика-1Филатов Александр Юрьевич
(Главный научный сотрудник, доцент ШЭМ ДВФУ)
alexander.filatov@gmail.com
https://vk.com/alexander.filatov, https://vk.com/baikalreadings
https://youtube.com/alexanderfilatov
Практика-1
Введение в эконометрику.
Корреляционный анализ
2.
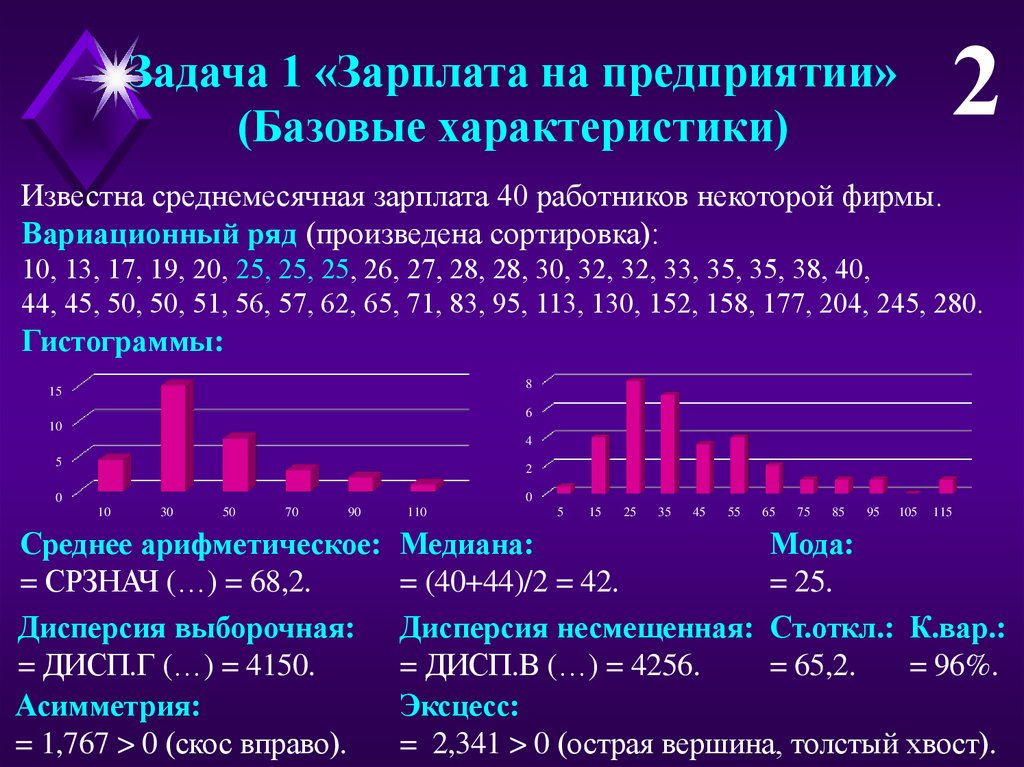
2Задача 1 «Зарплата на предприятии»
(Базовые характеристики)
Известна среднемесячная зарплата 40 работников некоторой фирмы.
Вариационный ряд (произведена сортировка):
10, 13, 17, 19, 20, 25, 25, 25, 26, 27, 28, 28, 30, 32, 32, 33, 35, 35, 38, 40,
44, 45, 50, 50, 51, 56, 57, 62, 65, 71, 83, 95, 113, 130, 152, 158, 177, 204, 245, 280.
Гистограммы:
8
15
6
10
4
5
2
0
0
10
30
50
70
90
Среднее арифметическое:
= СРЗНАЧ (…) = 68,2.
Дисперсия выборочная:
= ДИСП.Г (…) = 4150.
Асимметрия:
= 1,767 > 0 (скос вправо).
110
5
15
25
35
45
55
65
75
85
95
105
115
Медиана:
Мода:
= (40+44)/2 = 42.
= 25.
Дисперсия несмещенная: Ст.откл.: К.вар.:
= ДИСП.В (…) = 4256.
= 65,2.
= 96%.
Эксцесс:
= 2,341 > 0 (острая вершина, толстый хвост).
3.
Задача 2 «Стаж и зарплата»(Показатели парной связи)
3
Известна не только среднемесячная зарплата 40 работников, но и их стаж.
10, 13, 17, 19, 20, 25, 25, 25, 26, 27, 28, 28, 30, 32, 32, 33, 35, 35, 38, 40,
5, 2, 3, 1, 2, 1, 2, 4, 15, 3, 1, 9, 5, 3, 8, 2, 4, 14, 10, 5,
44, 45, 50, 50, 51, 56, 57, 62, 65, 71, 83, 95, 113, 130, 152, 158, 177, 204, 245, 280.
8, 12, 3, 28, 17, 6, 31, 7, 30, 10, 7, 22, 6, 24, 11, 7, 19, 13, 8, 18.
300
Коэффициент корреляции:
= КОРРЕЛ (х; y) = 0,350.
250
Проверка гипотезы о наличии связи:
α = 0,05,
200
150
y = -0,3775x2 + 13,665x - 3,4281
R² = 0,2901
100
y = 2,7607x + 41,509
R² = 0,1223
50
0
0
5
10
15
20
25
30
35
tкрит= СТЬЮДРАСПОБР(0,05;38)=2,024,
tэмп>tкрит, связь есть при α = 0,05.
При α < 0,027 связи нет.
4.
Задача 2 «Стаж и зарплата»(Показатели парной связи)
4
Доверительный интервал для коэффициента корреляции:
γ = 0,95, z = ФИШЕР(0,350) = 0,365, z~ = 0,365 – 0,350/2/39 = 0,361,
u(1+0,95)/2 = u0,975 = 1,96,
r1 = ФИШЕРОБР(0,038) = 0,038, r2 = ФИШЕРОБР(0,683) = 0,593.
300
Корреляционное отношение:
Отсортируем все данные по стажу и
проведем их разбивку на 4 интервала:
x (0;5], x (5;10], x (10;20], x>20,
n1 = 16, n2 = 11, n3 = 8, n4 = 5,
250
200
150
y = -0,3775x2 + 13,665x - 3,4281
R² = 0,2901
100
y = 2,7607x + 41,509
R² = 0,1223
50
0
0
5
10
15
20
25
30
35
5.
Задача 2 «Стаж и зарплата»(Показатели парной связи)
5
Проверка гипотезы о наличии связи произвольного вида:
Fкрит = FРАСПОБР(α; n – s; s – 1) = FРАСПОБР(0,05; 40 – 4; 4 – 1) = 2,866.
Fэмп > Fкрит, связь некоторого вида есть при α = 0,05.
При α < 0,003 связи нет.
Доверительный интервал для корреляционного отношения:
6.
6Спасибо
за внимание!
alexander.filatov@gmail.com
https://vk.com/alexander.filatov, https://vk.com/baikalreadings
https://youtube.com/alexanderfilatov





 mathematics
mathematics








