Similar presentations:
Линейная алгебра. Матрицы и их свойства
1.
Матрицы и их свойстваПрямоугольная числовая таблица из m строк и n столбцов
называется матрицей размерности m n:
a11
a
21
A
m n .
am1
a12
a22
.
am 2
... a1n
... a2 n
.
.
... amn
Пример:
2 1 4
A 6 2 8
3 3
0
3
6
Числа, составляющие матрицу, называются элементами
матрицы. Если m=n, то матрица называется квадратной
матрицей порядка n.
2.
a1a
1. Вектор-столбец - матрица размера m 1: 2
am
2. Вектор-строка - матрица размера 1 n: A=(a1 a2…an)
В квадратной матрице
элементы
a11,
a22,…ann
a11
a
21
A
.
an1
a12
a22
.
an 2
образуют
... a1n
... a2 n
.
.
... ann
главную
диагональ,
а элементы an1, an-1 2,…a1n – побочную диагональ матрицы.
3.
3. Матрица, у которой всенулевой матрицей (обозначение 0).
элементы
aij=0,
называется
4. Диагональной матрицей называется квадратная матрица,
в которой все элементы, кроме элементов главной диагонали,
равны 0.
1 0 ... 0
0
1
...
0
называется единичной.
5. Квадратная матрица E
. . . .
0
0
0
1
6. Матрица –А(mxn) называется матрицей противоположной
матрице А (mxn).
4.
Операции над матрицами1. Сравнение
Две матрицы А и В одинаковой размерности равны, если у них
равны элементы, расположенные на соответствующих местах.
2. Сложение
Суммой двух матриц A и B одинаковой размерности
называется матрица С той же размерности, каждый элемент
которой равен сумме соответствующих элементов матриц А и В.
Для того, чтобы найти разность матриц одинаковой
размерности А и В нужно из каждого элемента матрицы А вычесть
соответствующий элемент матрицы В.
5.
Свойства:1) А + В = В + А
2) (А + В) + С = А + (В + С)
3) А + 0 = А
4) А + (–А) = 0
Пример: Пусть
Тогда
2 5 6
A
,
0 4 1
3 2 4
B
.
0 5 7
1 7 10
5 3 2
A B
, A B
,
0 9 6
0 1 8
2 5 6
A
.
0 4 1
6.
3. Умножение матрицы на действительное числоПроизведением матрицы А(mxn) на число R называется
матрица той же размерности, полученная из матрицы А
умножением всех элементов на число .
Свойства:
1) 1 ·А = А
2) ( +μ) ·А = ·А +μ ·А
3) ·(А + В) = ·А + ·В
4) ( · μ) ·А = · (μ · А) = μ · ( · А)
2 5 6
Пример: Пусть A
,
0 4 1
тогда
4 10 12
2 A
.
0 8 2
7.
4. Умножение вектора-строки на вектор-столбецПроизведением вектора-строки А(1 n) на вектор-столбец В(n 1)
называется число, равное сумме произведений соответствующих
элементов А и В:
A В a11 a12
b11
n
b
21
... a1n
a1i bi1
i 1
bn1
8.
5. Умножение двух матрицПусть
a11
a21
A
.
am1
a12
a22
.
am 2
... a1n
... a2 n
.
.
... amn
b11 b12 ... b1k
b
b
...
b
2k
B 21 22
.
.
.
.
bn1 bn 2 ... bnk
Произведением матрицы А (m n) на матрицу В (n k)
называется матрица С (m k) , элементы сij которой равны
сумме произведений элементов i-ой строки матрицы А на j-ый
столбец матрицы В:
n
Сij aip bpj
p 1
9.
Свойства:1) А · В В · А
2) А · (В + С) = А · В + А · С
3) (В + С) · А = В · А + С · А
4) (А · В) · С = А · (В · С)
5) А · 0 = 0,
0·А=0
6) А · Е = А,
Е· А = А
10.
Пример: Найти произведение матриц A 1 1 B 2 4 1 .0
3
1
1 0
1 2 ( 1) 0 1 4 ( 1) 3 1 1 ( 1) ( 1) 2 1 2
A B
.
1 4 0 3
1 1 0 ( 1) 2 4 1
1 2 0 0
Степень Аn = A · A · … · A
Свойства:
1) А0 = Е, если матрица А невырожденная
2) Аp · Аq = Аp+q
3) (Аp)q = Аpq
11.
6. Транспонирование матрицМатрица АТ (nxm) , получаемая из данной матрицы А(mxn)
путем
замены
i-ой
строки
на
транспонированной к матрице А.
Пример:
1 2 3
A
,
2x3 4 5 6
Свойства:
1) ( · А)T = · АT
2) (А + В)T = АT + BT
3) (АT)T = А
4) (А · В)T = ВT · AT
i-ый
столбец,
1 4
AT 2 5
3 6
3x2
называется




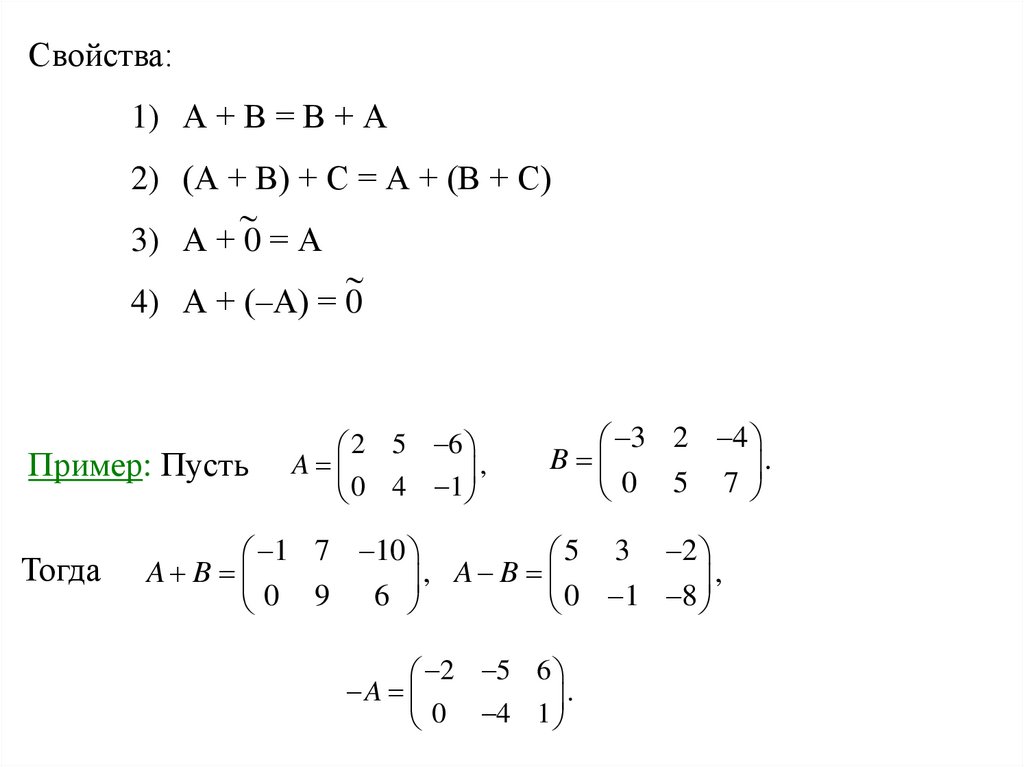






 mathematics
mathematics








