Similar presentations:
Техника вычисления пределов
1. ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
2. 1.Предел функции в точке.
lim f ( x)x a
3. 1.1. Предел многочлена.
lim P( x) P(a)x a
lim( x 5 x 4) 2 5 2 4 2
3
x 2
3
4. 1.2.Предел дробно-рациональной функции.
P( x)lim
x a R( x)
5. Раскрытие неопределенности
00
разложите числитель или (и)
знаменатель на множители,
сократите дробь,
вычислите предел.
6. Примеры:
x 2 0x 2
1) lim 2
lim
x 2 x 4
0 x 2 x 2 x 2
1
1
1
lim
lim
x 2 x 2
x 2 2 2
4
x 10 x 3
x 2 13 x 30 0
2) lim
lim
2
x 10
100 x
0 x 10 10 x 10 x
x 3
7
lim
0.35
x 10 10 x
20
7. 1.3. Предел иррациональной функции. Раскрытие неопределенности
1.3. Предел иррациональнойфункции.
0
Раскрытие неопределенности
0
домножить
числитель и знаменатель
дроби на выражение, сопряженное
числителю или (и) знаменателю,
упростить выражение и сократить дробь,
вычислить предел.
8. Примеры:
1 x 1 1 x 11 x 1 0
lim
lim
x 0
x
0 x 0
x 1 x 1
lim
x 0
1 x 1
x 1 x 1
x 0
x
x 1 x 1
1
lim
0.5
x 0
1 1
1 x 1
1
lim
9. 2. Предел функции на бесконечности .
lim f ( x)x
10. 2.1.Раскрытие неопределенности
11. Примеры: большая степень числителя превышает большую степень знаменателя, следовательно, предел стремится к бесконечности.
x 7x / x 7/ x
1) lim 2
lim 2 3
3
x 5 x / x 4 / x
x 5 x 4
3
1 7 / x
3
3
3
1 0
1
lim
lim
lim
3
x
x 0 0
x 0
5/ x 4/ x
3
12. Примеры: большая степень числителя совпадает с большей степенью знаменателя, следовательно, предел - отличное от нуля число.
6 x3 3x 16 x 3 / x 3 3 x / x 3 1/ x 3
2) lim
lim
3
3
3
3
x
5x 2
5x / x 2 / x
x
6 3 / x 1/ x
2
lim
x
5 2/ x
3
3
6 0 0 6
lim
1.2
x
5 0
5
13. Примеры: большая степень числителя меньше большей степени знаменателя, следовательно, предел равен нулю.
3x 4 x3x / x 4 x / x
3) lim
lim
6
6
6
6
7 x 8 x 7 x / x 8 / x
x
3
3
3/ x 4/ x
3
lim
x
7 8/ x
3
5
6
0 0
lim
0
x 7 0
6
14.
3. Замечательныепределы.
15. 3.1. Первый замечательный предел.
limx 0
lim
x 0
sin
sin
1
1
16. Примеры:
sin 5 x 0sin 5 x 5
1) lim
lim
x 0
x
5
0 x 0 x
sin 5 x 5
lim
1 5 5
x 0
5x 1
sin13x 0
sin13x 13
2) lim
lim
x 0 sin 8 x
8
0 x 0 sin 8 x















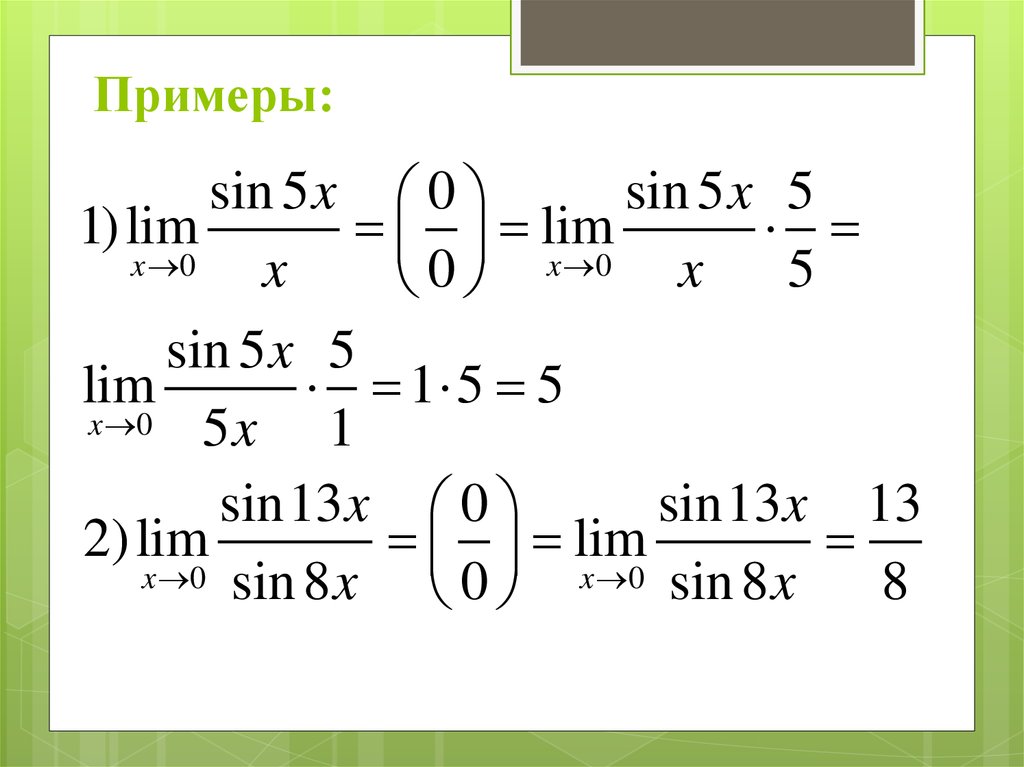
 mathematics
mathematics








