Предел функции в точке

1. Предел функции в точке

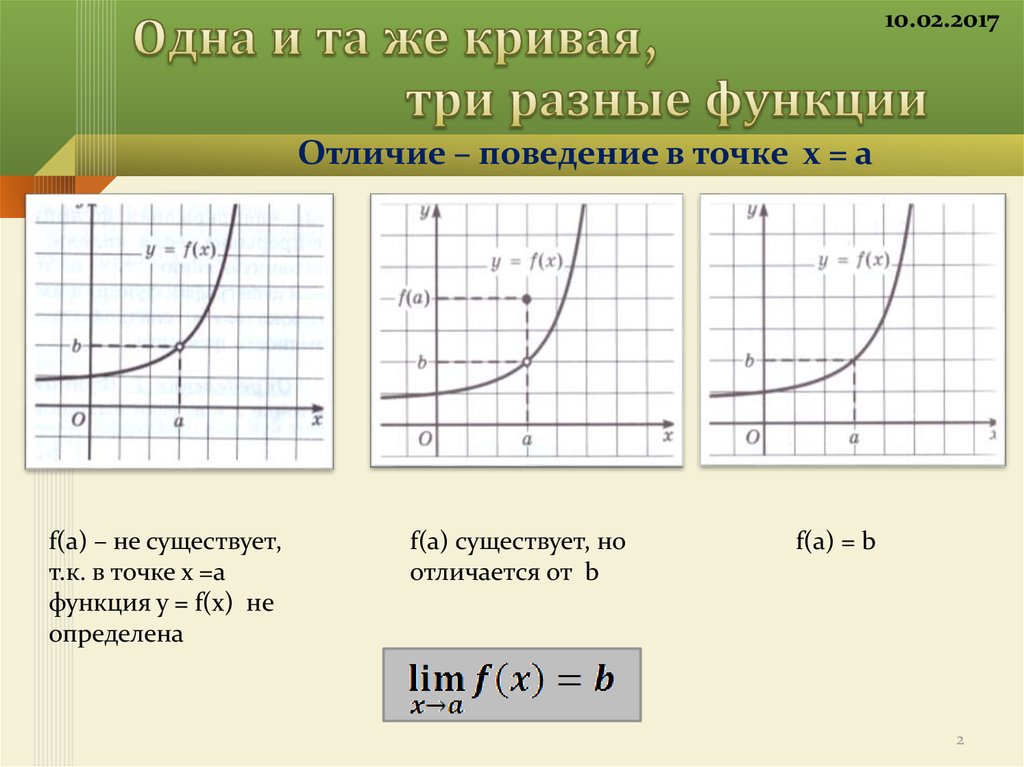
2. Одна и та же кривая, три разные функции

10.02.2017
Отличие – поведение в точке х = а
f(a) – не существует,
т.к. в точке х =а
функция у = f(х) не
определена
f(a) существует, но
отличается от b
f(a) = b
2

3.

Определение. Функцию у = f(х) называют
непрерывной в точке х = а, если выполняется
соотношение
Функцию у = f(х) называют непрерывной на
промежутке Х, если она непрерывна в каждой
точке промежутка.
Если выражение f(х) составлено из рациональных,
иррациональных, тригонометрических и
обратных тригонометрических выражений, то
функция у = f(х) непрерывна в любой точке , в
которой определено выражение f(х).
10.02.2017
3

4. Вычисление пределов функции

10.02.2017
Правила вычисления пределов.
Если
,
, то
1. Предел суммы равен сумме пределов.
+
= b+c
2. Предел произведения равен произведению пределов
=b•c
3. Предел частного равен частному пределов (с 0)
= b/c
4.
4

5. Вычисление пределов

Вычисление предела:
lim f ( x ) A
x x0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0

6. Вычисление пределов

Часто при подстановке предельного значения x0 в функцию f(x)
получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление пределов
в этом случае называется раскрытие неопределенности.

7.

10.02.2017
7

8. Раскрытие неопределенностей

Раскрытие неопределенности
0
0
x 2 14x 32
0
x 2 x 16
lim 2
lim
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
lim
x 0
Если f(x) – дробно –
рациональная функция,
x 1 1 x 1 1
0 на
x 1 1
необходимо разложить
lim Если f(x) – иррациональная
множители числитель
и x 0 дробь, необходимо умножить
0
x
x x 1 1
знаменатель дроби
числитель и знаменатель дроби
x 1 1
на1выражение,1сопряженное
lim
lim
числителю.
x 0
x 0
x x 1 1
x 1 1 2

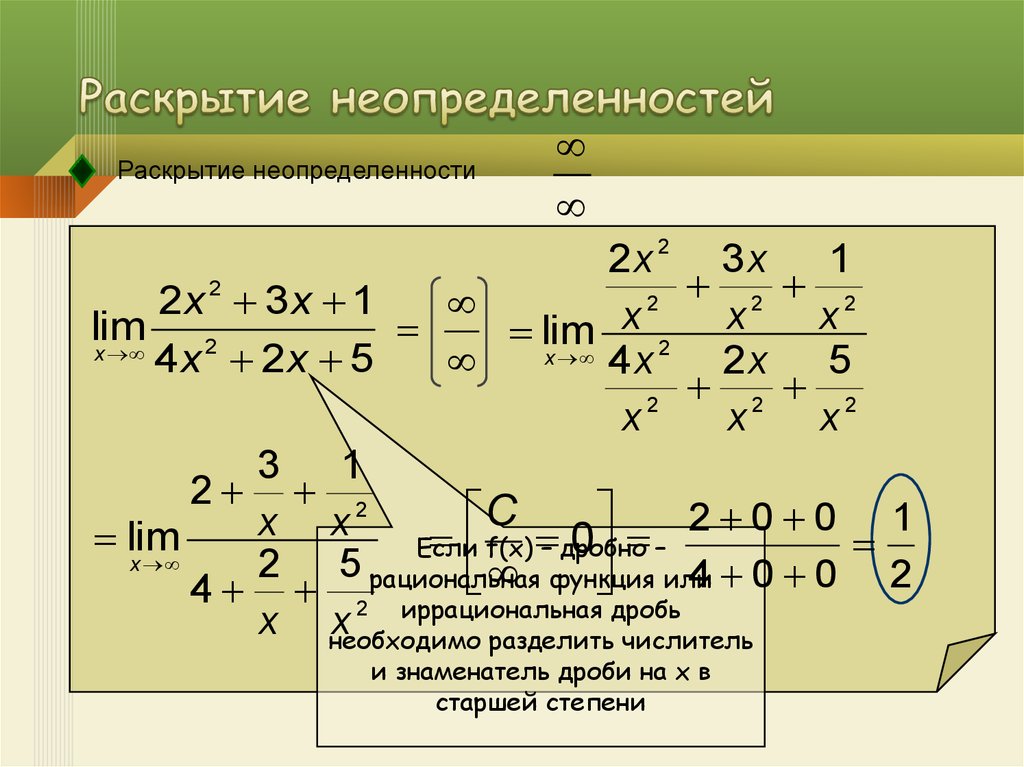
9. Раскрытие неопределенностей

Раскрытие неопределенности
2
2x
3x 1
2 2
2
2x 2 3 x 1
x
x
x
lim 2
lim
x
x 4 x 2
4 x 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5 рациональная
4 0 0 2
функция
или
4 2 иррациональная
дробь
x необходимо
x
разделить числитель
и знаменатель дроби на x в
старшей степени

10. Раскрытие неопределенностей

Раскрытие неопределенности
2
2
lim
x
1
x
1
x
lim
x
lim
x
x 1 x 1
2
2
Умножим
2
2
0
и разделим функцию
1сопряженное
)
на
выражение.
x 1 x 1
2
2
x2 1 x2 1
( x 1) ( x
2
x 1 x 1
2
2
lim
x
2
x 1 x 1
2
2

11. Первый замечательный предел

sin 2 x
1 cos 4 x 0 lim 2 sin 2x 2 lim
2
x
0
lim
x 0
x
2
x
x 0
0
x
2
2
sin 2 x
2 sin 2 x
2 lim
2 lim
x 0
x 0
x
2x
2
2
sin 2 x
2
2 2 lim
2 2 1 8
x 0
2x
2

12. Выполнить задания

10.02.2017
• В классе:
• №39.23(а,б)№39.25(а,б);
• № 39.29(а,б)
Дома:
№39.23(в,г);
№ 39.27(в,г);
№39.29(в)
12

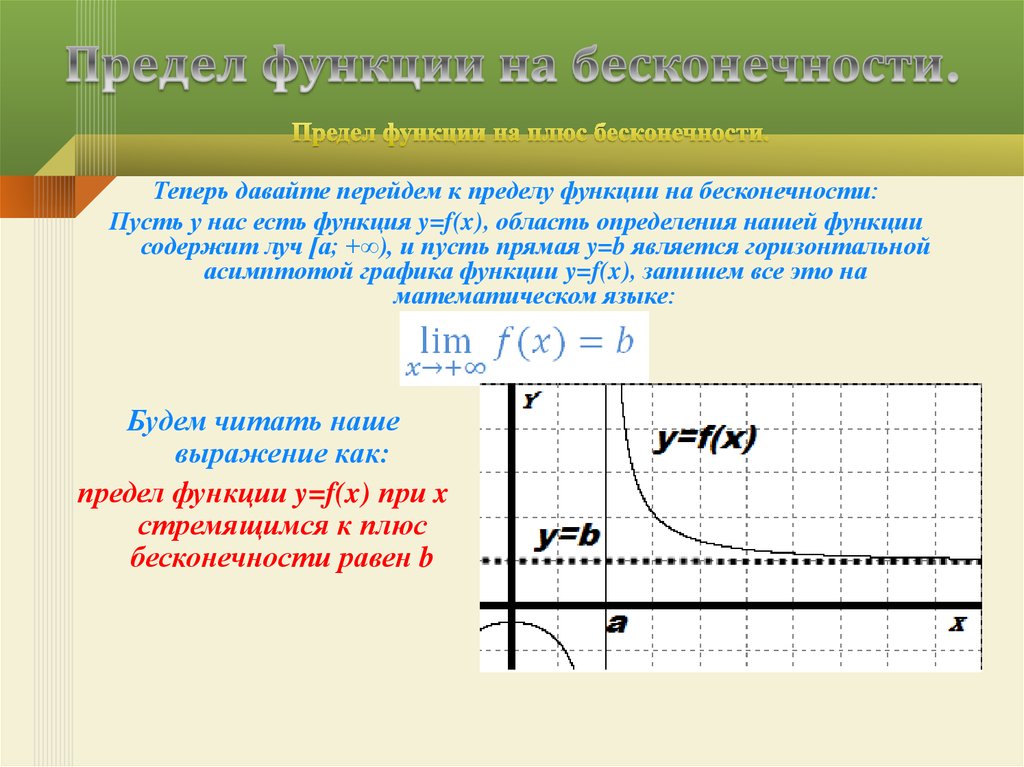
13. Предел функции на бесконечности.

Теперь давайте перейдем к пределу функции на бесконечности:
Пусть у нас есть функция y=f(x), область определения нашей функции
содержит луч [a; +∞), и пусть прямая y=b является горизонтальной
асимптотой графика функции y=f(x), запишем все это на
математическом языке:
Будем читать наше
выражение как:
предел функции y=f(x) при x
стремящимся к плюс
бесконечности равен b

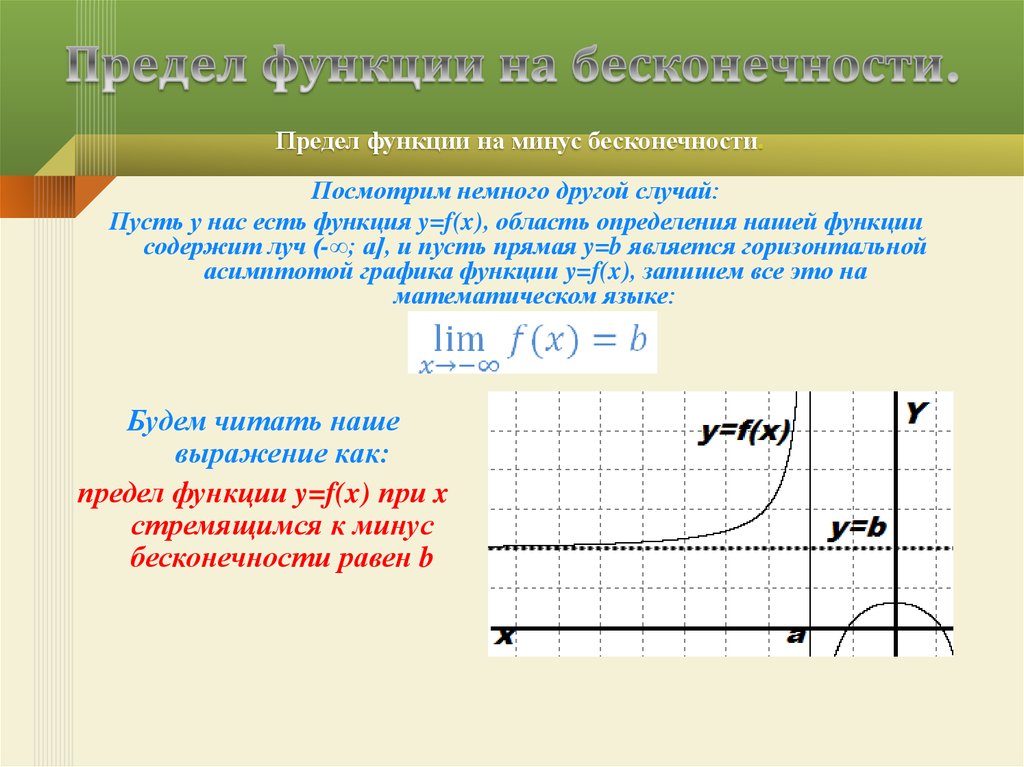
14. Предел функции на бесконечности.

Предел функции на минус бесконечности
Посмотрим немного другой случай:
Пусть у нас есть функция y=f(x), область определения нашей функции
содержит луч (-∞; a], и пусть прямая y=b является горизонтальной
асимптотой графика функции y=f(x), запишем все это на
математическом языке:
Будем читать наше
выражение как:
предел функции y=f(x) при x
стремящимся к минус
бесконечности равен b

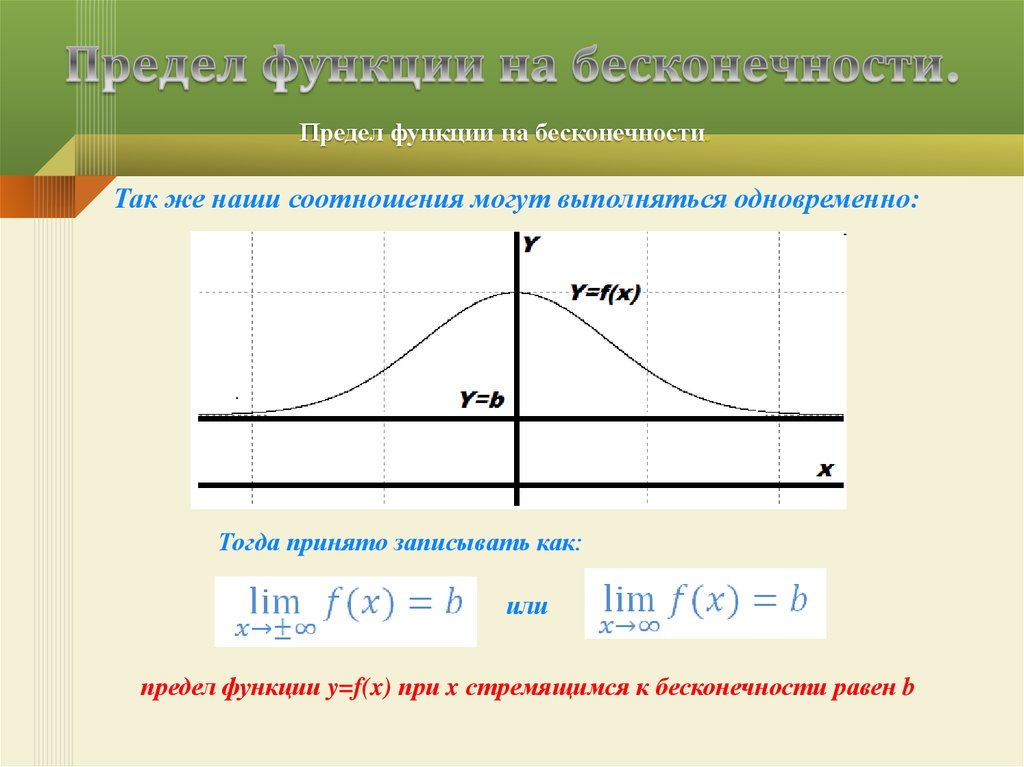
15. Предел функции на бесконечности.

Предел функции на бесконечности
Так же наши соотношения могут выполняться одновременно:
Тогда принято записывать как:
или
предел функции y=f(x) при x стремящимся к бесконечности равен b

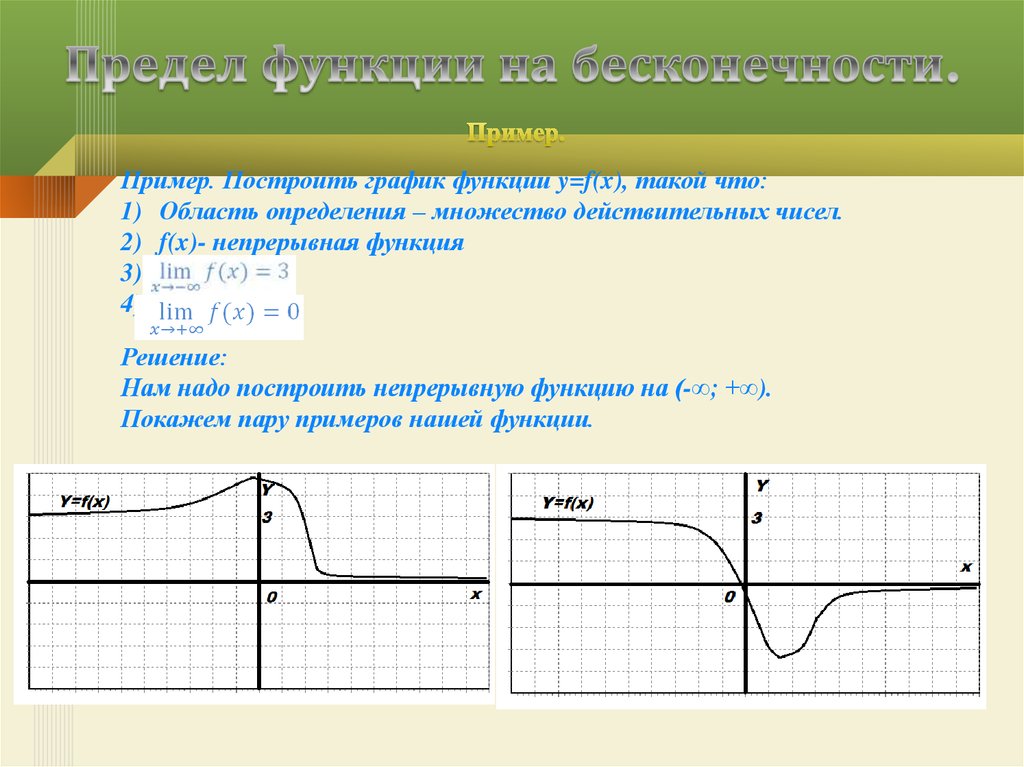
16. Предел функции на бесконечности.

Пример. Построить график функции y=f(x), такой что:
1) Область определения – множество действительных чисел.
2) f(x)- непрерывная функция
3)
4)
Решение:
Нам надо построить непрерывную функцию на (-∞; +∞).
Покажем пару примеров нашей функции.

17. Предел функции на бесконечности.

Основные свойства.
Для вычисления предела на бесконечности пользуются несколькими
утверждениями:
1) Для любого натурально числа m справедливо следующее
соотношение:
2) Если
то:
а) Предел суммы равен сумме пределов:
б) Предел произведения равен произведению пределов:
в) Предел частного равен частному пределов:
г) Постоянный множитель можно вынести за знак предела:

18. Предел функции на бесконечности.

Пример. Найти
Решение.
Разделим числитель и знаменатель дроби на x.
Воспользуемся свойством предел частного равен частному пределов:
Получим:
Ответ:

19. Предел функции на бесконечности.

Пример. Найти предел функции y=f(x), при x стремящимся к
бесконечности.
Решение.
Разделим числитель и знаменатель дроби на x в третьей степени.
Воспользуемся свойствами предела на бесконечности
Предел числителя равен: 5-0=5; Предел знаменателя равен: 10+0=10

20. Предел функции на бесконечности.

Пример. Найти предел функции y=f(x), при x стремящимся к
бесконечности.
Решение.
Разделим числитель и знаменатель дроби на x в третьей степени.
Воспользуемся свойствами предела на бесконечности
Предел числителя равен: 0; Предел знаменателя равен: 8

21. Предел функции на бесконечности.

1) Построить график непрерывной функции y=f(x). Такой
что предел при x стремящимся к плюс бесконечности
равен 7, а при x стремящимся к минус бесконечности 3.
2) Построить график непрерывной функции y=f(x). Такой
что предел при x стремящимся к плюс бесконечности
равен 5 и функция возрастает.
3) Найти пределы:
4) Найти пределы:

22. Использованная литература

• Мордкович А.Г., Семенов П.В. «Алгебра и
начала математического анализа.
Профильный уровень». 10 класс.
22