Similar presentations:
General problem of mathematical programming
1. General problem of mathematical programming
f ( y) min, y Q R N(1)
Q { y D : g j ( y ) 0, 1 j m}
(2)
D { y R N : yi [ai , bi ], 1 i N }
(3)
h( y) 0 ~ h( y) , 0
h( y ) 0,
h( y ) 0
h(y) 0,
0, y Q,
(Q)
1, y Q,
- характеристическая функция множества Q
(Q ) 0
Nested optimization scheme
1
2. Auxiliary functions and sets
Feasibility function G ( y ), y D :G ( y ) 0, y Q,
(4)
G ( y ) 0, y Q.
G( y) max{ g1 ( y),..., g m ( y)}
(5)
G( y) max{ 0; g1 ( y),..., g m ( y)}
(6)
ui ( y1 , , yi ), vi ( yi 1 , , y N ), 1 i N 1,
(7)
u N y, i N ,
v0 y, i 0.
S1 Q,
Si 1 (ui ) {vi R
N i
: (ui , vi ) Q}, 1 i N 1
i 1 (ui ) { yi 1 R1 : ( yi 1 , vi 1 ) Si 1 (ui )}
Nested optimization scheme
(8)
(9)
2
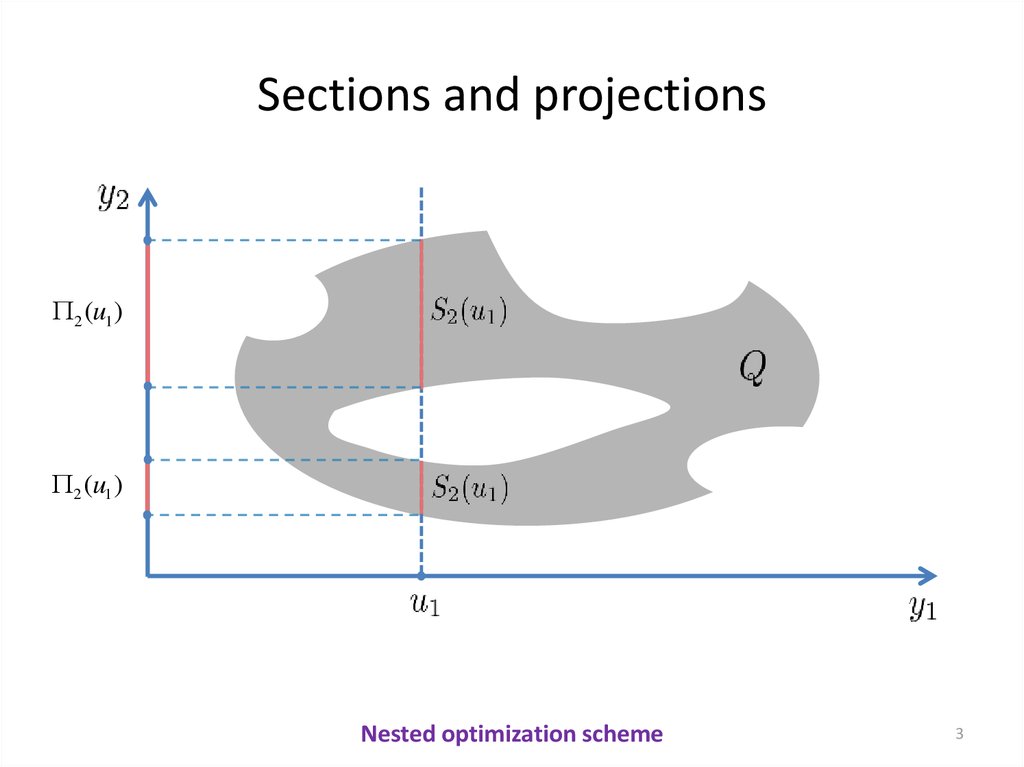
3. Sections and projections
2 (u1 )2 (u1 )
Nested optimization scheme
3
4. Reducing the feasibility function
G N ( y ) G( y )G i (ui ) min{ G i 1 (ui , yi 1 ) : yi 1 [ai 1 , bi 1 ]}, 1 i N 1,
(10)
Di {ui Ri : y j [a j , b j ], 1 j i}
(11)
LEMMA 1
Gi (ui ) min{ G(ui , vi ) : y j [a j , bj ], i 1 j N}
Projecting Q onto coordinate axes
y1 , , yi :
Qi {ui R i : (ui , vi ) Q}, 1 i N .
(12)
(13)
(14)
LEMMA 2
Qi {u i R i : G i (u i ) 0}
(15)
LEMMA 3
i 1 (ui ) { yi 1 [ai 1 , bi 1 ] : G i 1 (ui , yi 1 ) 0}
Nested optimization scheme
(16)
4
5. Nested optimization scheme
f N ( y) f ( y)f i (ui ) min{ f i 1 (ui , yi 1 ) : yi 1 i 1 (ui )}, ui Qi
(17)
Main relation
min f ( y) min min ...
y Q
y1 1 y2 2 ( u1 )
min
y N N ( u N 1 )
f ( y)
(18)
f 1 ( y1 ) min, y1 1 R1
1 { y1 [a1 , b1 ] : G 1 ( y1 ) 0}
f 2 ( y1 , y2 ) min, y2 2 ( y1 ) R1 ,
2 ( y1 ) { y 2 [a 2 , b2 ] : G 2 ( y1 , y 2 ) 0}
f 3 (u2 , y3 ) min
. . .
f N (u N 1 , y N ) f (u N 1 , y N ) min, y N N (u N 1 ).
Nested optimization scheme
5
6. Nested optimization scheme
f i (ui 1 , yi ) min, yi i (ui 1 )(19)
ui 1 Qi 1 fixed
extr extr ...
y1 1 y2 2 ( u1 )
extr ( y)
yN N ( uN 1 )
y2
Example
f ( y1 , y2 ) ( y1 1) 2 ( y2 1) 2
g1 ( y) y1 y2 1
1
0 y1 2, 0 y2 2
1
Nested optimization scheme
y1
6
7. Nested optimization scheme
G 2 ( y ) y1 y2 1G1 ( y1 ) min{ y1 y2 1, y2 [0, 2]} y1 1
2 ( y1 ) { y2 [0, 2] : y1 y2 1 0} [0, 1 y1 ]
1 { y1 [0,2] : y1 1 0} [0, 1]
f 2 ( y1 , y2 ) ( y1 1) 2 ( y2 1) 2
f 1 ( y1 ) min{( y1 1) 2 ( y2 1) 2 : y2 2 ( y1 ) [0, 1 y1 ]}
Функция ( y1 1) 2 ( y2 1) 2 достигает минимума по y2 в единице,
а слева от 1 убывает, поэтому на отрезке [0, 1 y1 ] ее минимум
достигается в точке y2 1 y1 , а значение равно 2 y12 2 y1 1 , т.е.
f 1 ( y1 ) 2 y12 2 y1 1
Ее минимум на отрезке [0,1] достигается в точке y1* 1 / 2
f 2 (0.5, y2 ) 1 / 4 ( y2 1) 2
Т.к. 2 (1/ 2) [0,1 1/ 2] [0,1/ 2] , где f
*
убывает, то y2 1 / 2
Nested optimization scheme
2
7
8. Структура допустимых областей одномерного поиска
G(y) – непрерывна в D и все G i (u i ) непрерывны по u i Di и, следовательно,по yi [ai , bi ].
Т.к. в (19) ui 1 фиксирован о , любая задача (19) может быть представлена в виде
( x) min, x Q R1
(20)
Q {x [a, b] : g ( x) 0}
где функция g (x ) непрерывна.
q
Q [a j , b j ]
(21)
j 1
Nested optimization scheme
8
9. Структура допустимых областей одномерного поиска
g (x)1
x sin , x 0,
x
0,
, x 0,
qi
i (u i 1 ) [a ij , bi j ]
j 1
qi qi (u i 1 )
a ij a ij (u i 1 )
bi j bi j (u i 1 )
Когда qi 1 i (ui 1 ) [ai , bi ] ?
1. Q D
1
1
2. Q - выпуклое множество
3. Q - ограничения g j ( y ) монотонно унимодальны.
Nested optimization scheme
9
10. Свойства целевых функций в одномерных подзадачах
iЦелевая функция в одномерной задаче (19) – это функция f (u i 1 , y i ) при
фиксированном ui 1
Сепарабельные функции
N
f ( y ) f i ( yi )
i 1
в гиперпараллелепипеде Q D
N
min f ( y ) min
y Q
i 1
yi [ ai , bi ]
f i ( yi )
Условие Липшица
f ( y ) f ( y ) L y y , y , y Q
f i (u i ) - липшицевы по yi ?
Nested optimization scheme
10
11. Свойства целевых функций в одномерных подзадачах
Рассмотрим областьQ { y R 2 : y12 y22 1 0}
2
Тогда f ( y) f ( y) - липшицева с константой L
1
Однако f ( y1 ) липшицевой не является: она удовлетворяет условию Гельдера
f ( y1 ) f ( y1 ) L1 y1 y1
с константой L1 L(1 2 )
Сохранение липшицевости - область Q - выпуклый многогранник.
Nested optimization scheme
11










 mathematics
mathematics








