Similar presentations:
Компьютерные технологии принятия решений в формализованных и неформализованных задачах
1.
Кафедра радиотехникиМетоды оптимизации
и исследование операций
Дисциплина ОПД.Ф.10
Бугров Владимир Николаевич
Доцент радиофизического факультета
ННГУ им.Н.И. Лобачевского
2.
Кафедра радиотехникиКомпьютерные технологии
принятия решений в формализованных и неформализованных
задачах
Бугров Владимир Николаевич
Доцент радиофизического факультета
ННГУ им.Н.И. Лобачевского
3.
Общая структура курсаСистемный
базис
Оптимизация
Базовые
задачи
исследования
операций
Методы
решения
неформализованных задач
Исследование операций (ИО)
Экстремальная мат.задача (ЭМЗ)
Анализ
Решение задач
ИО методами
оптимизации
Системная
психология
Принятие решений (ПР)
Математическое программирование (МП)
Синтез
Управление
Список литературы
3
4.
Базовые определенияРешение - всякий определённый выбор параметров задачи (объекта)
X ( x1 , x2 , x3 ... x )
xi E
(1)
Оптимизация - методология повышения качества объекта или процесса
по заданному критерию (критериям)
Математическое программирование – изучение постановки и методологии
решения экстремальных математических задач:
ext F ( X ) (2)
X D
Операция - всякое мероприятие (система действий), объединённое единым
замыслом и направленное на достижение определённой цели
Исследование операций - применение математических, количественных
методов для обоснования решений во всех областях целенаправленной
человеческой деятельности
Принятие решений - процедура определения (и выбора) ОПТИМАЛЬНОГО
по заданному критерию(-ям) решения в допустимой области D
o
o
o
o
o
X ( x1 , x 2 , x 3 ... x )
xi D
Управление - процедура принятия решений во времени
о
Х (t )
4
5.
Формализованные задачи принятия решений1. Математические задачи:
б) решение систем трансцендентных уравнений
в) решение систем неравенств
г) решение нелинейных диффер. уравнений
2. Физические задачи:
а) модельная аппроксимация интерферометрического сигнала
б) многокритериальный синтез дискретных сигналов
3. Задачи проектирования (компьютерные САПР РЭУ)
4. Экономические и финансовые задачи:
а) реинжиниринг бизнес-процессов
б) оптимизация продаж в рамках эластичности спроса
в) организация производства под заданный рынок сбыта
г) экспертиза и оптимизации структуры землепользования
5. Типовые задачи исследования операций:
а) организация производства и транспорта
б) организация медицинского обслуживания
в) организация поставок и сбыта товаров
г) управление продажами в рамках заданного спроса
д) организация противолодочного рейда
5
6.
Задачи системной психологииСистемная психология - изучение вопросов поведения (принятия решений,
управления деятельностью) в адаптивных биологических системах
Системный анализ - Теория систем - Теория управления
80 - 20
Психологическая
компетенция
1. Определение психики, индивида
2. Основной вопрос психологии
3. Системный базис психологии
4. Сознание, его определение и
значимость
5. Механизмы психического
управления деятельностью
Есть ли ум у кошки?
6. Классификация личности
по уровню сознания
6
7.
Два уровня логического познанияСознание (ум) - это способность психики к опосредованной
логической обработке информации на понятийном уровне.
Математическая логика
НАУКА
Наука - логическое познание заданной предметной
области на количественном уровне
Качественная логика
ИСКУССТВО
КУЛЬТУРА
Искусство – важнейший способ эстетического
освоения мира (?)
Чувственный образ
Логическое понятие
Матем.формула
8.
Статистика смертностич
е
л
о
в
е
к
Психо-соматические заболевания - 90 %
60
%
24
15
10
~ 10 млн
7
Сердечнососудистые
Онкология
50
30
Старость Несчастный
случай
Эндокрин.
(диабеты)
Старость
(склерозы)
8
5
Онкология,
диабет
Сердечнососудистые
Суицид
Суицид
8
9.
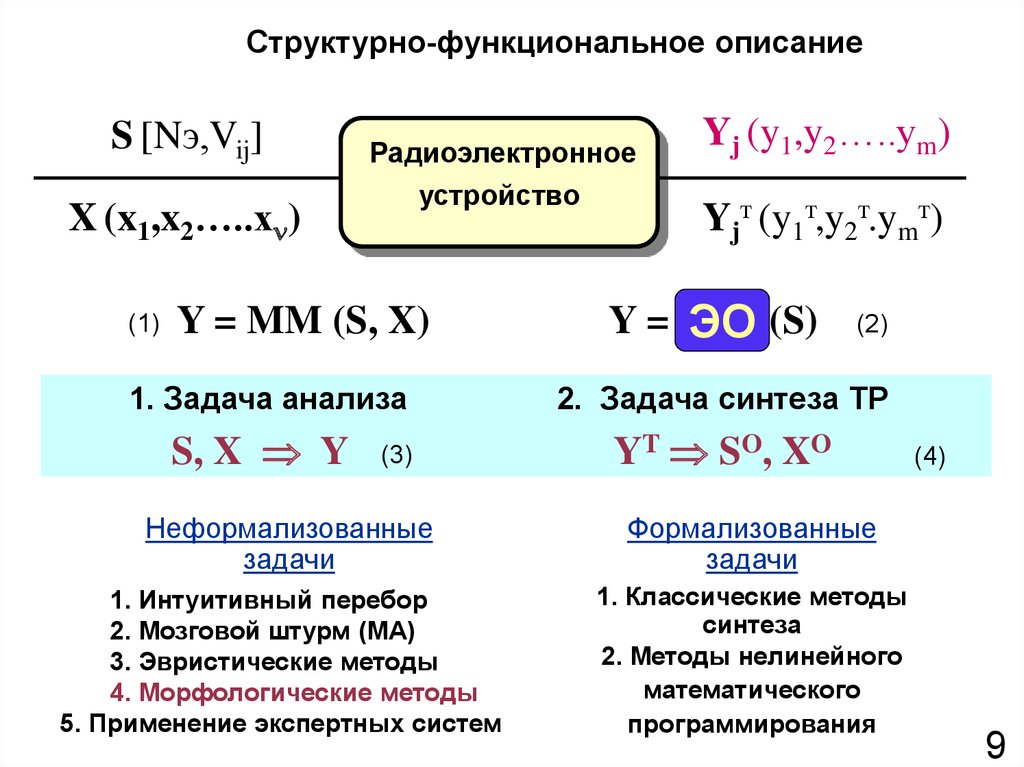
Структурно-функциональное описаниеS [Nэ,Vij]
X (x1,x2…..x )
(1)
Радиоэлектронное
устройство
Y = MM (S, X)
Yj (y1,y2…..ym)
Yjт (y1т,y2т.ymт)
Y = ЭО (S)
(2)
1. Задача анализа
2. Задача синтеза ТР
S, X Y
YT SO, XO
(3)
Неформализованные
задачи
1. Интуитивный перебор
2. Мозговой штурм (МА)
3. Эвристические методы
4. Морфологические методы
5. Применение экспертных систем
(4)
Формализованные
задачи
1. Классические методы
синтеза
2. Методы нелинейного
математического
программирования
9
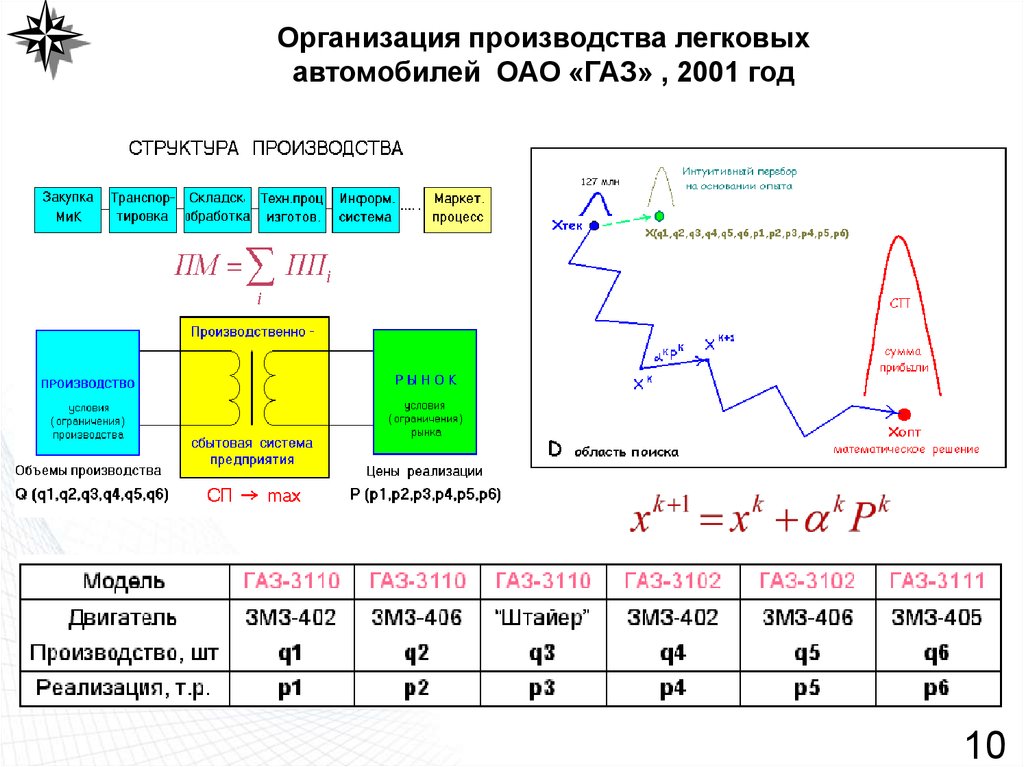
10. Организация производства легковых автомобилей ОАО «ГАЗ» , 2001 год
1011. Постановка задачи многофункционального синтеза РЭУ в пакете ЛиПС 4.0
1112. Классификация радиотехнических цепей
1. Линейные стационарные цепиT ( U Вх1 U Вх2 ) TU Вх1 TU Вх2
U Вых (t to) T U Вх (t to) - условие стационарности
uc q / c
di
L ri uc 0
dt
(1)
r
q q 2 q 0
L
линейные ДУ
2. Линейные нестационарные (параметрические) цепи
T ( U Вх1 U Вх2 ) TU Вх1 TU Вх2
di
q
L ri
0
dt
C (t )
3. Нелинейные цепи
r 1 sin H t
q q
q 0
L
LC0
(2)
y ( y ) y 0
По критерию соотношения характерных размеров
цепи делятся на:
С(t ) C0 / (1 sin H t )
а) Сосредоточенные
б) Распределённые
i
- нелинейные ДУ
c длиной волны
i λ
i λ
(3)
λ
(RLC-цепи)
(длинные линии)
12
13.
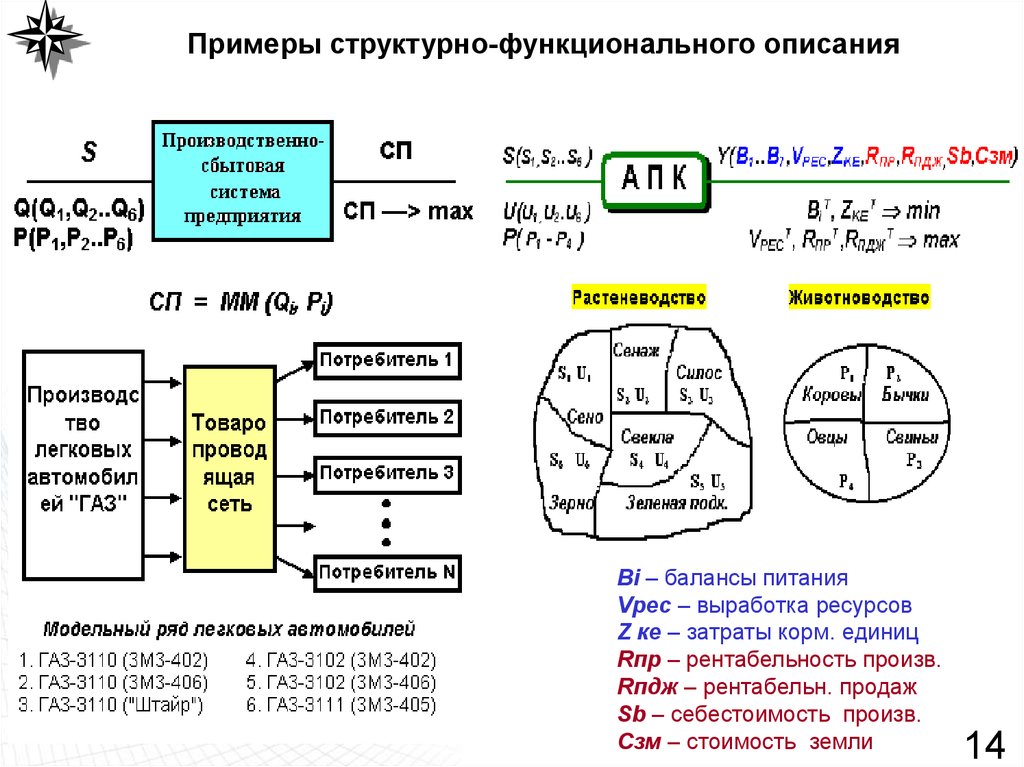
1314. Примеры структурно-функционального описания
Вi – балансы питанияVрес – выработка ресурсов
Z кe – затраты корм. единиц
Rпр – рентабельность произв.
Rпдж – рентабельн. продаж
Sb – себестоимость произв.
Cзм – стоимость земли
14
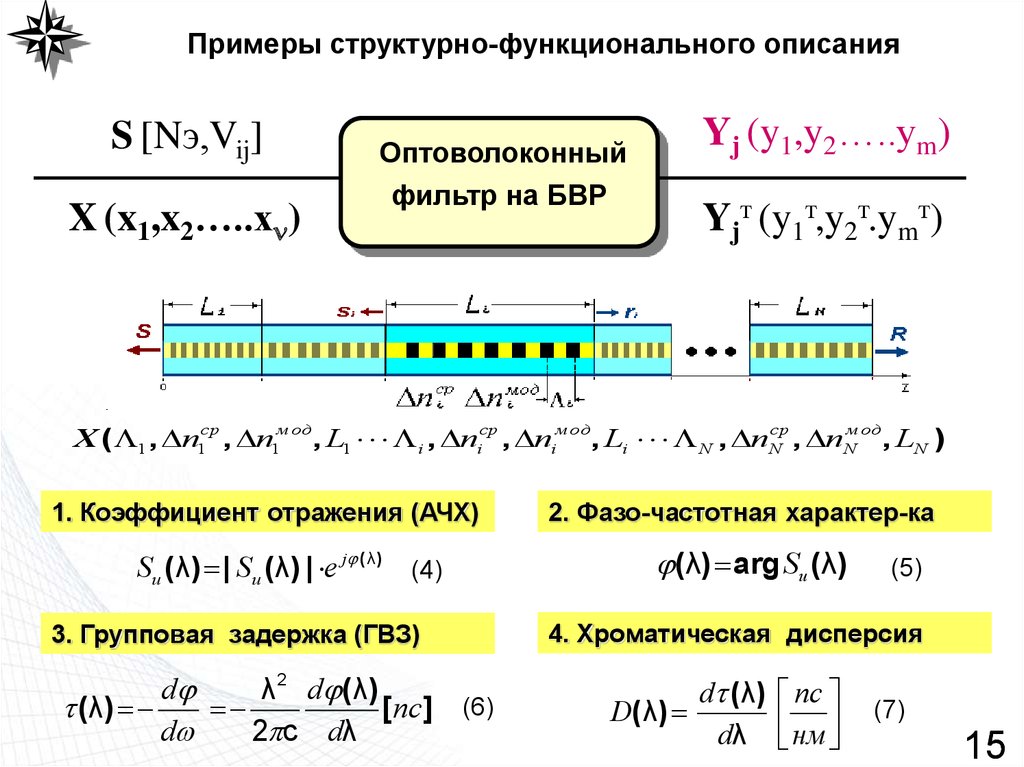
15. Примеры структурно-функционального описания
S [Nэ,Vij]X (x1,x2…..x )
Yj (y1,y2…..ym)
Оптоволоконный
фильтр на БВР
Yjт (y1т,y2т.ymт)
X ( 1 , n1ср , n1м од, L1 i , niср , niм од, Li N , nNср , nNм од, LN )
1. Коэффициент отражения (АЧХ)
Su (λ) | Su (λ) | e j ( λ ) (4)
3. Групповая задержка (ГВЗ)
d
λ 2 d (λ)
( λ)
[ пс ] (6)
d
2 c dλ
2. Фазо-частотная характер-ка
(λ) arg Su (λ)
(5)
4. Хроматическая дисперсия
D( λ )
d (λ)
dλ
пс
нм
(7)
15
16.
Примеры структурно-функционального описаниярезультаты
действий
структура
S(Nэ)
X[x1(t)...xv(t)]
действия
(поведение)
ИНДИВИД
(АбиоС)
Y[y1(t)...ym(t)]
YT[yT1(t)...yTm(t)]
мотивации
(потребности)
16
17. Классификация задач синтеза
Синтез – определение оптимального внутреннего состоянияКлассификация задач синтеза
объекта (идеального технического решения - SO и XO ) по
требуемому функционированию YT (техническому заданию).
I. Структурный синтез – определение оптимальной структуры SO по
требуемому функционированию YT объекта:
Y S
T
II.
Параметрический
синтез
параметров ХO объекта:
–
o
определение
оптимальных
Y X | s const
T
o
III. Структурно-параметрический синтез – определение оптимальной
структуры SO и параметров ХО объекта:
Y S ,X
T
o
o
17
18. Современные тенденции синтеза
I. Многофункциональность – синтез по совокупности функциональных характеристик объекта (АЧХ, ФЧХ, КСВ ..):F ( X ) i fi ( X )
i
2. Многопараметрический синтез – размерность пространства
параметров до нескольких сотен и даже тысяч.
3.
Дискретизация пространства параметров (дискретные . ряды
Е6, Е12, Е24 - Е192, целочисленная дискретизация и др.).
4.
Синтез с учетом внешних условий
функциональных ограничений Gi(X).
5.
Основная методология
методы математического
программирования, максимально
ориентированные
на
современные вычислительные системы.
решения
задачи
-
18
19.
ЭКСПЕРТНАЯ ОБОЛОЧКАMORFEX
оптимизации и экспертизы структуры
неформализованных объектов, систем
и процессов любой природы
Основные отличия и достоинства морфологической экспертизы:
1. Осуществление структурной декомпозиции исследуемого объекта или процесса на
базе структурно-функционального подхода. Простая и наглядная форма
отображения структуры объекта в виде морфологической таблицы
2. Возможность многокритериальной экспертизы и синтеза структуры объекта с
указанием требуемой значимости экспертных критериев
3. Выявление структурно-функциональной связи (удовлетворения экспертных критериев) методом экспертных оценок. Единственный субъективный этап метода
4. Результатом как экспертизы, так и синтеза оптимальной структуры является
численная оценка, пропорциональная совокупному качеству объекта экспертизы
5. Относительно недорогая компьютерная реализация морфологического метода за
счет отсутствия базы знаний и эвристик (системы искусственного интеллекта)
19
20. Основные задачи, решаемые ЭС «МОRFEX»
Многокритериальная оценка качества объектовРасчет групповых рейтингов или общего рейтинга
структурированного множества объектов или
процессов по различным основаниям (условиям)
Экспертиза заданной структуры объекта
Сравнительная экспертиза нескольких структур
объектов или процессов по совокупности критериев
Синтез оптимальной структуры объекта
Синтез наихудшей структуры объекта
Хранение текстовой и графической информации
по каждому объекту в базе данных системы
20
21. Системы морфологической экспертизы
Экспертизаинвестиций и
инноваций
Экспертиза
и оптимизация
технологических
процессов
Экспертиза
поставок и сбыта
ПОСТАВКИ
Экспертная
оболочка
MORFEX
РЕИНЖИНИРИНГ
бизнес-процессов
Управление
персоналом
ПЕРСОНАЛ
Экологическая
экспертиза
ЭКОЛОГИЯ
Морфологический
синтез технических
решений
21
22.
Основные недостатки классических методов синтеза (ПР)1) Неинвариантность методики решения относительно объекта
синтеза, т. е. для различных РЭУ должна разрабатываться
своя методика синтеза и
собственное
программное
обеспечение:
2) С возрастанием сложности задачи (сложности математической модели, с
увеличением числа показателей и числа переменных ) аналитическое
решение задачи становиться затруднительным, а затем и невозможным;
3) Полная непригодность классических
методов для синтеза по
совокупности требуемых, зачастую противоречивых, характеристик. То есть
много-функциональный синтез невозможен классическими
методами
теории цепей.
4) Не позволяют осуществить синтез для произвольной, наперед заданной
структуры РЭУ.
5) Классические методы непригодны и при наложение ограничений на
значения параметров цепи. Так режим дискретного синтеза параметров
здесь невозможен.
6) Методы классического синтеза не позволяют определять значения токов и
напряжений в ветвях синтезируемой цепи, необходимых для энергетического
расчета устройства.
23. Целевая функция экстремальной задачи синтеза
oo
F ( X ) min F ( X )
X D
о
Х
о
Х
o
o
F ( X ) min F ( X )
X D
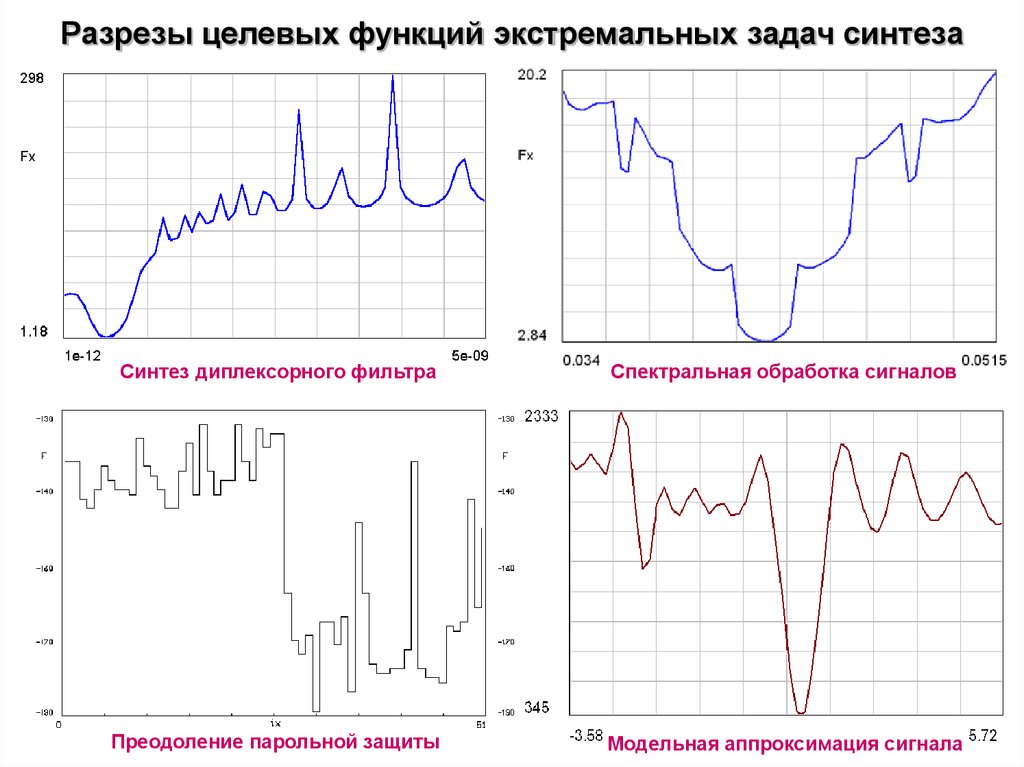
24. Разрезы целевых функций экстремальных задач синтеза
Синтез диплексорного фильтраСпектральная обработка сигналов
Преодоление парольной защиты
Модельная аппроксимация сигнала
25. Формирование относительных показателей функционирования (частных критериев синтеза)
ki i ( yi )K [ k1 ( X ), k2 ( X ) ... km ( X )]
1) обеспечение
нормирования
частных
критериев, приведение их к безразмерному
виду;
2) зависимость I должна отражать правило
предпочтения одного варианта другому, т.е.
экстремум ki(X) дoлжен доставлять объекту
требуемое качество (требуемые значения
частных абсолютных показателей
yiT ).
T
yi ( X ) yi
ki ( X )
yiT
(1)
Виды сходимостей
1. Ненормированный квадратичный критерий
ki ( X ) [ yi ( X ) yiT ] 2
(2)
2. Критерий типа « не выше yiT »
y ( X ) yT
i
i
T
ki ( X )
yi
0
при yi ( X ) yiT
(3)
при yi ( X ) yiT
3. Критерий типа « не ниже yiT »
y ( X ) yT
i
i
T
ki ( X )
yi
0
при yi ( X ) yiT
(4)
при yi ( X ) yiT
4. Критерий на максимальное значение yi мах
ki ( X )
Формирование ki в виде - парабол
1
yi ( X )
(5)
25
26. Эффективное решение векторной экстремальной задачи
kk1 Х ,
1
Х min
x D
*
*
*
*
X x1 , x2 ,..., x
*
min K (X )
(1)
X D
k* Х* min k Х ,
x D
2
2
. . . . . . .
* *
k m Х min k Х
m
x D
Скаляризация векторной задачи
О
F Х min F Х
x D
О
(2)
26
27. Парето-эффективное решение проектной задачи
АЧХf АЧХ ( X )
(1)
ФЧХ
fФЧХ ( X )
КСВ
f КСВ ( X )
K ( j ) H ( )
ГВЗ
Дисперсия
1 p
f i ( X ) СКО
Yn ( X ) YnT
p n 1
F ( X ) i f i (X)
2
(2)
i
k
СКО ( ) const
N
o
o
F ( X ) min F ( X )
(3)
D
2 R 1 ai , bi 2 R 1 1 (4)
Z pi 1 i 1, m
(5)
K imin | K i (e j ) | K imax ,
27
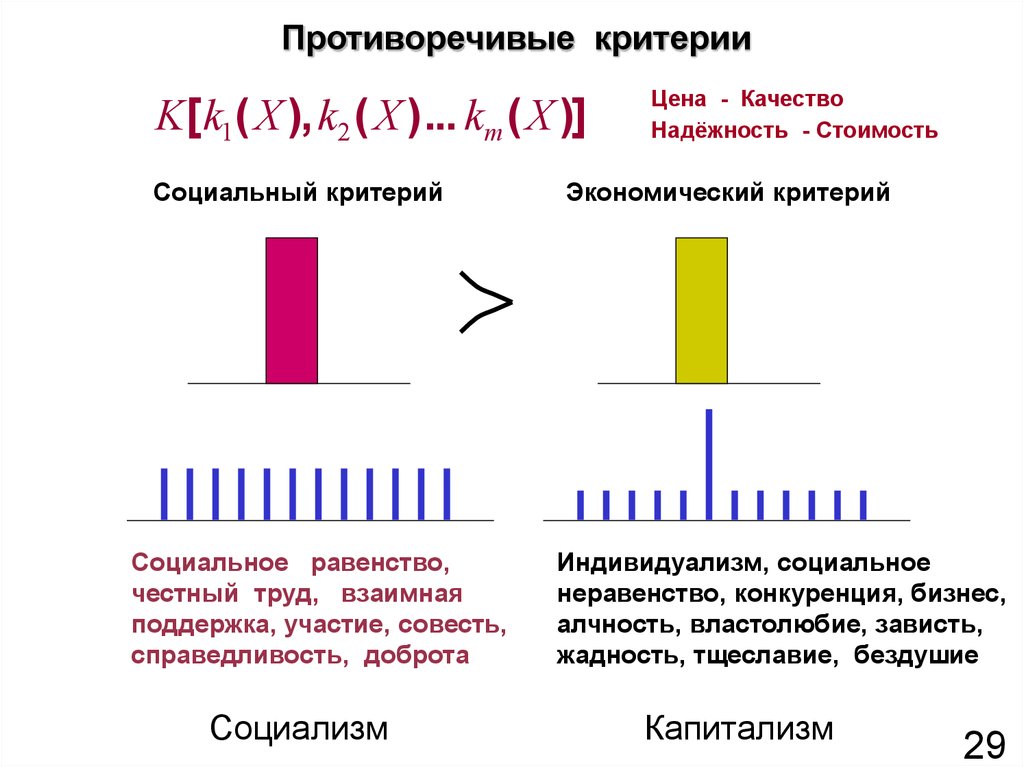
28. Противоречивые критерии
2829. Противоречивые критерии
K [ k1 ( X ), k2 ( X ) ... km ( X )]Социальный критерий
Социальное равенство,
честный труд, взаимная
поддержка, участие, совесть,
справедливость, доброта
Социализм
Цена - Качество
Надёжность - Стоимость
Экономический критерий
Индивидуализм, социальное
неравенство, конкуренция, бизнес,
алчность, властолюбие, зависть,
жадность, тщеславие, бездушие
Капитализм
29
30. Формирование целевых функций в задачах многокритериального синтеза
Целевая функция F(X) формируются в функциональном редакторе пакета изчастных критериев ki(X) одним из следующих методов:
1. Метод главного критерия
F X k X
i
ki Ai ,
2. Метод обобщенного критерия
m
F X i ki X
(2)
i 1
(1)
m
F X ki i X
(3)
i 1
3. Метод минимаксного критерия
F X max k1 , k 2 ,..., k max ki ( X )
i
F X min f i x min max ki ( X )
x D
i
x D
(4)
(5)
4. Метод последовательных уступок
k1 ( X ) k3 ( X ) k7 ( X ) ... k ( X )
F X kn X
k n An ,
n 1,
- приоритетный ряд
(6)
30
31. Задача нелинейного математического программирования в общей трактовке
oo
F ( X ) min F ( X )
X PX
PX E S I B
n
m
p
(1)
q
(2)
xiн xi xiв i 1,
(3)
g j ( X ) 0 j 1,
(4)
Высокая размерность
экстремальной задачи
Нелинейность, полимодальность целевой
функции (1)
Неоднородность (2)
пространства поиска
Прямые ограничения в
виде гиперкуба (3)
Система нелинейных
функциональных
ограничений (4)
En – непрерывное вещественное пространство размерностью n
Sm –дискретное вещественное пространство размерностью m
Ip – счетное целочисленное пространство размерностью p
Bq –пространство булевых переменных размерностью q
=n+m+p+q
31
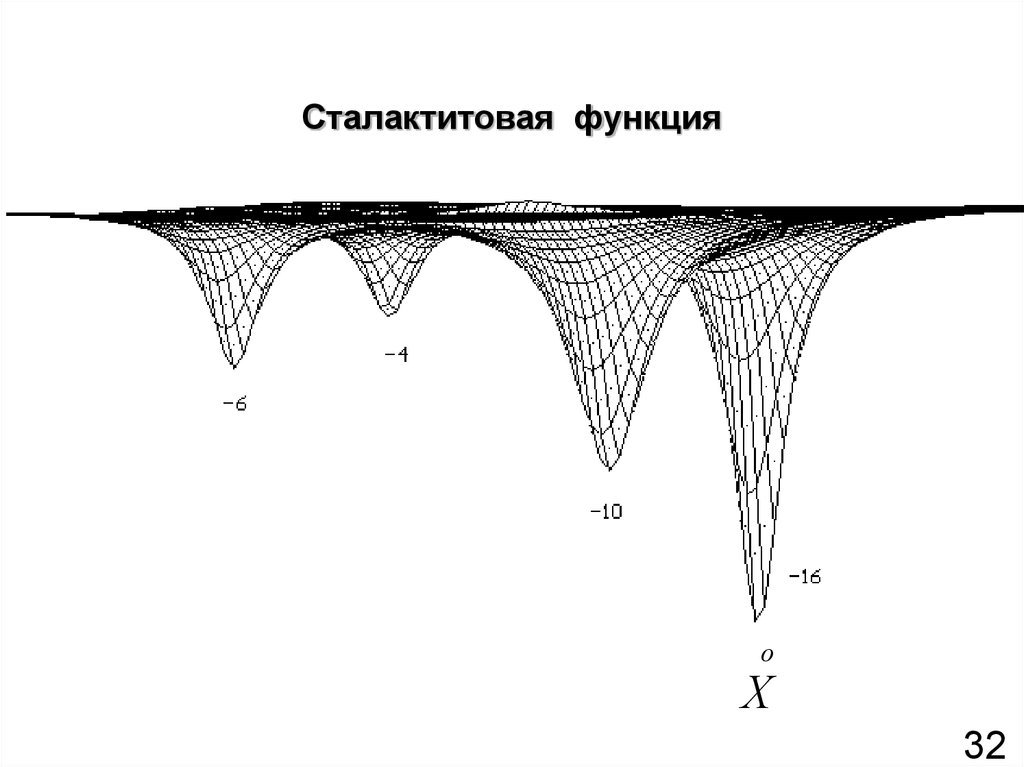
32. Сталактитовая функция
оХ
32
33. Общая структура численного решения
I.Методология разрешения заданной
функциональных ограничений задачи
основе комбинированного штрафа.
системы
gi(X)
на
II.
Разработка
базовых итеративных алгоритмов
нулевого порядка для минимизации полимодальных
ЦФ в пространствах En, Sm, Ip и Bq
III. Идеология взаимодействия базовых алгоритмов при
минимизации
в
неоднородном
пространстве
параметров РХ. Предложена и реалиована параллельная схема взаимодействия базовых алгоритмов.
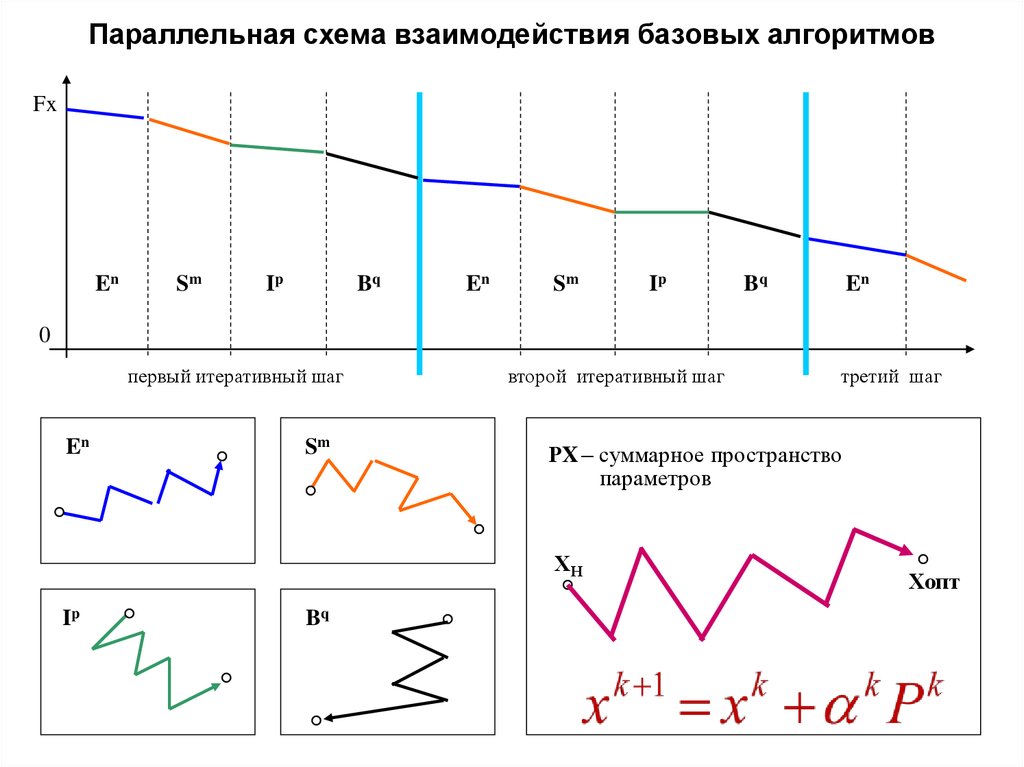
34. Параллельная схема взаимодействия базовых алгоритмов
FxEn
Sm
Ip
Bq
En
Sm
Ip
Bq
En
0
первый итеративный шаг
En
Sm
второй итеративный шаг
РX – суммарное пространство
параметров
ХН
Ip
Bq
третий шаг
Хопт
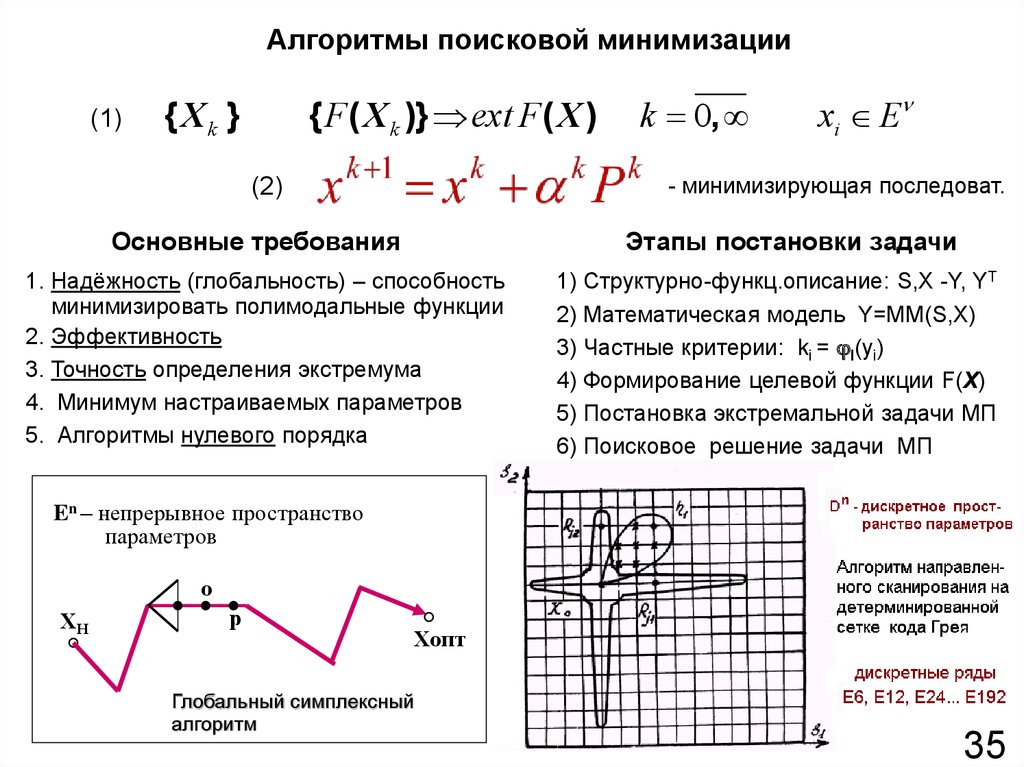
35. Алгоритмы поисковой минимизации
(1){ F ( X k )} ext F ( X )
{ Xk }
k 0,
xi E
- минимизирующая последоват.
(2)
Основные требования
Этапы постановки задачи
1. Надёжность (глобальность) – способность
минимизировать полимодальные функции
2. Эффективность
3. Точность определения экстремума
4. Минимум настраиваемых параметров
5. Алгоритмы нулевого порядка
1) Структурно-функц.oписание: S,X -Y, YT
2) Математическая модель Y=MM(S,X)
3) Частные критерии: ki = I(yi)
4) Формирование целевой функции F(X)
5) Постановка экстремальной задачи МП
6) Поисковое решение задачи МП
En – непрерывное пространство
параметров
о
ХН
р
Глобальный симплексный
алгоритм
Хопт
35
36. Типовая структура программы синтеза
Функциональныйредактор (формир ЦФ)
Топологический
редактор (ввод схемы)
Алгоритмический комплекс
решения общей задачи НМП
Модуль анализа
и расчета ЦФ
нет
Y(X) = YT
Анализ оптимального
решения в ЧО
Анализ допусков
Исследование ЦФ
Стационарная
(RLC) модель
I
j
0
j
YU=I
уравнение
состояния
( СЛУ )
Y – матрица узловых проводимостей
Протокол синтеза
36
37. Аналоговые радиоэлектронные программные пакеты САПР
УНИВЕРСАЛЬНЫЕ ПАКЕТЫI. НИЗКОЧАСТОТНЫЕ (сосредоточенные цепи)
Метод
Micro_CAP
Метод
Стоимость
УПТ, BDF
10000$
УПТ
УПТ
Joint_CAP
ЛиПС
II. Пакеты СВЧ (микрополосковые линии, волноводы)
Метод
Стоимость
MicroWave
Office
S-параметры
МКР
60000$
MicroWave
Studio
S-параметры
МКР
80000$
Метод
МИКРОПОЛ
S-параметры
37
38.
СПЕЦИАЛИЗИРОВАННЫЕ ПАКЕТЫНазначение
1. Синтез устройств на ПАВ
2. Синтез активных фильтров
( ARC – схем )
Название
DSW
Заказчик
НПО «ПОЛЁТ»,
СИНТЕЗПРОМ
ВARC
З-д им. Г.И.Петровского
3. Целочисленный синтез цифровых
фильтров
DDF
З-д им. Г.И.Петровского
4. Синтез оптических устройств на
волоконных брэгговских решётках
DВF
ИРИТ
5. Синтез интегральных схем
LGTEX
LG Innotek
6. Многокритериальный синтез
дискретных сигналов
Barker
«КВАЗАР-КОМЕТА»
ВAR
«КВАЗАР-КОМЕТА»
CKиФ
НПО «ЭРКОН»
7. Параметрический синтез
активных селективных R-чипов
8. Синтез пассивной ЭКБ
38
39. Решение математических задач методами оптимизации
40.
Классические методы решенияЛинейные уравнения
ax b 0
a 0
x b/a
Нелинейные уравнения
b b 2 4ac
ax bx c 0 x1,2
2a
Системы уравнений
2
а1 x1 b1 x2 ... c1
a2 x1 b2 x2 .. c2
. . . . . . . . . . с
m
Системы неравенств
Методы математического
программирования
o
o
F ( X ) min F ( X )
X D
хiн хi хiв
0
0
0
(1)
(2)
0
X ( x1 , x2 , ... xm )
(3)
Целевая функция
40
41.
Постановка задачи математического программированияS
X (x1,x2…..xm)
1. Абсолютные показатели
Y (y1,y2…..ym)
Система
уравнений
fi(X)=0
Yт (y1т,y2т…ymт)
yi ( X ) f i ( X )
i 1, m
2. Формирование относительных показателей
(2)
y iT 0
(1)
ki
ki ( X ) [ yi ( X ) yiT ]2
3. Формирование целевой функции
m
F ( X ) i k i ( X )
YiT
(3)
i 1
4. Постановка экстремальной задачи МП
o
Yi
o
F ( X ) min F ( X )
X D
5. Решение задачи МП численными поисковыми методами
(4)
41
42.
Решение линейного уравнения методамиматематического программирования
42
43. Решение системы трансцендентных уравнений
Y ( y1 , y2 )(1)
X ( p, q)
F(x) min max{ k1 , k2 }
X D
k1 y
2
1
k2 y
2
2
10 p 10
D:
3 q 10
43
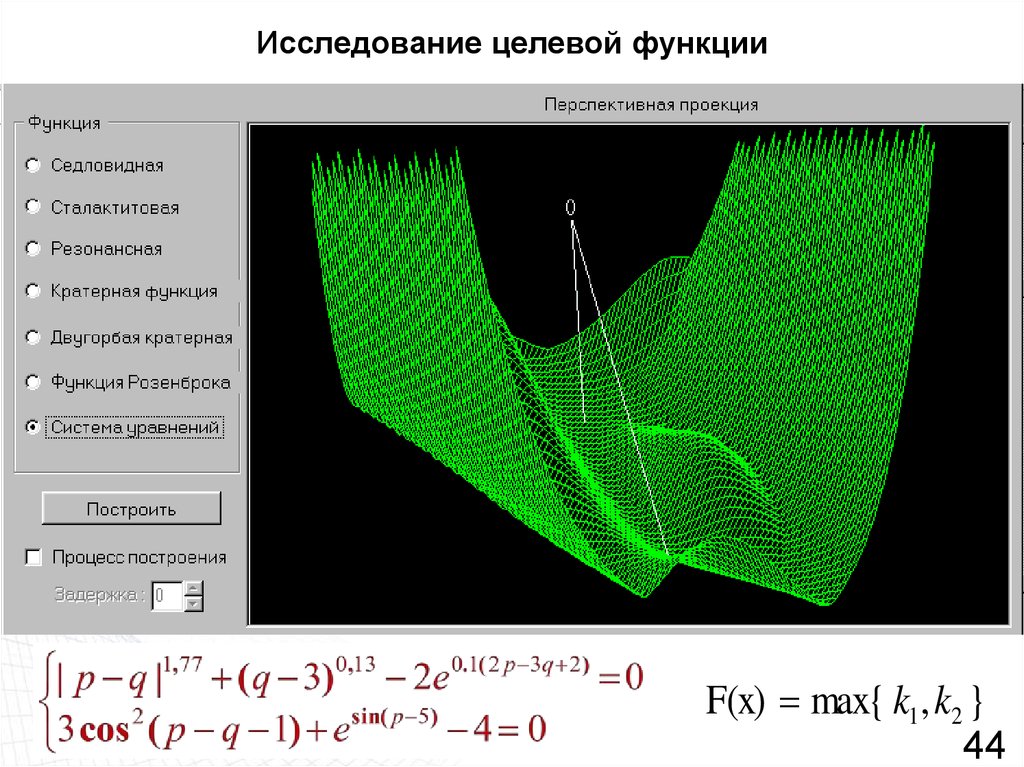
44. Исследование целевой функции
F(x) max{ k1 , k2 }44
45. Решение системы трансцендентных уравнений
p1 5q1 4
p2 7,16
q3 6,88
Время решения 15 сек
45
46. Вторая модель хозрасчёта предприятия
47. Вторая модель хозрасчёта предприятия
“не ниже yT”<
>=
o
yi
48.
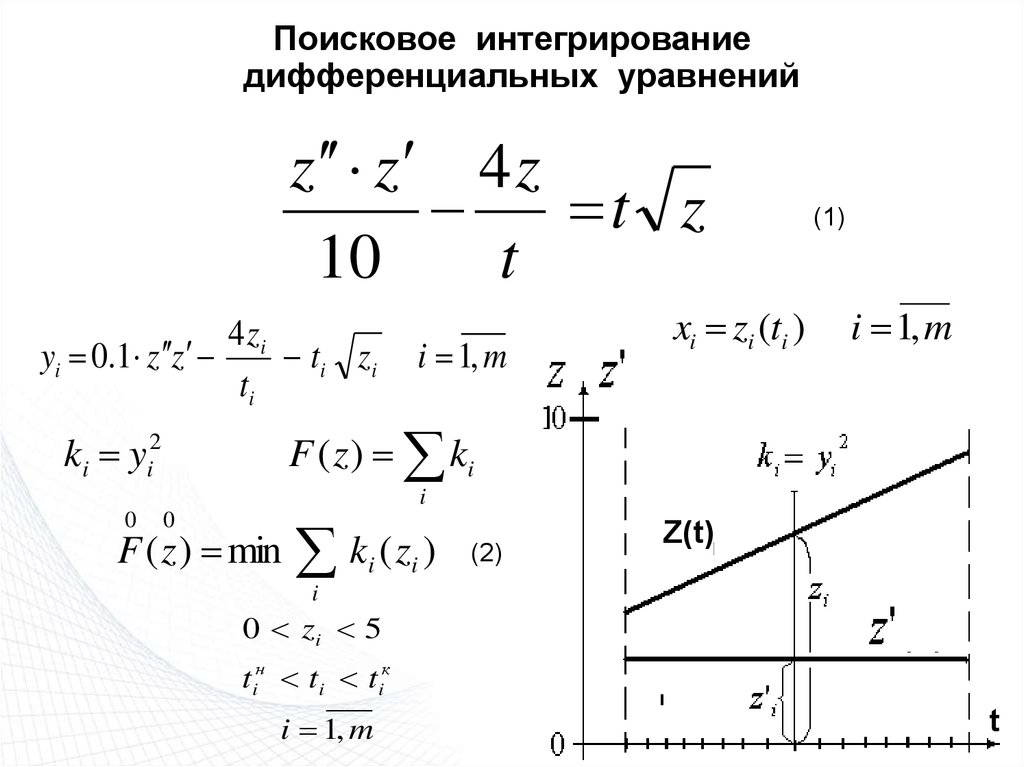
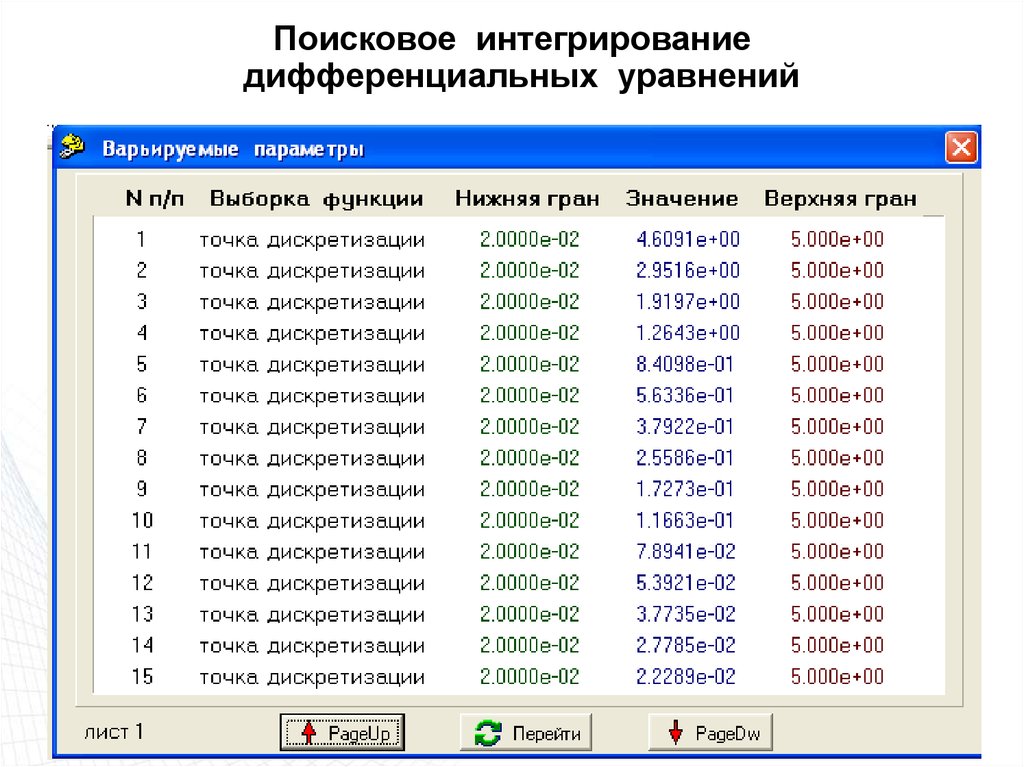
49. Поисковое интегрирование дифференциальных уравнений
z z 4 zt z
10
t
4 zi
yi 0.1 z z
ti zi
ti
i 1, m
xi zi (ti )
(1)
i 1, m
F ( z ) ki
ki yi2
i
0
0
F ( z ) min
k i ( zi )
(2)
Z(t)
i
0 zi 5
tiн ti tiк
i 1, m
t
49
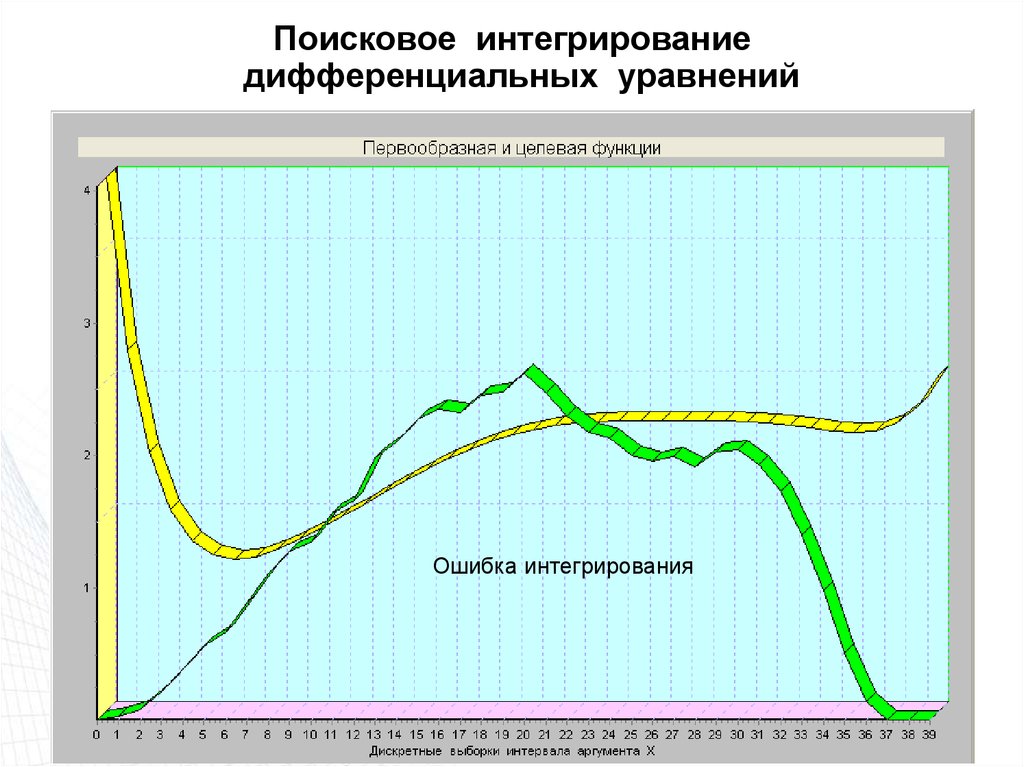
50. Поисковое интегрирование дифференциальных уравнений
Ошибка интегрирования51. Поисковое интегрирование дифференциальных уравнений
Ошибка интегрирования52. Поисковое интегрирование дифференциальных уравнений
53. Поисковое интегрирование дифференциальных уравнений
54.
Выводы1. Поисковые методы математического программирования являются
инвариантной методологией решения сложных математических
задач: трансцендентных уравнений и систем, систем неравенств,
нелинейных дифференциальных уравнений.
2.
Инвариантность определяется внешней идеологией решения, не
зависящая от сложности решаемой задачи. При решении математических задач методами МП не существует критерия сложности
задачи – необходима только её формализация.
Сложность
задачи
3.
Решение сложных задач нелинейного МП возможно только
поисковыми методами в многомерном пространстве параметров.
При этом возникает критерий надёжности решения, надёжности
поисковой минимизации полимодальных целевых функций.
54
55.
4. Математическая задача, решаемая поисковыми методами МП, можетне иметь аналитического выражения – данные, функциональ-ные
зависимости могут быть табулированы в таблицу. То есть возможна
прямая обработка данных, например, физических измерений без их
аналитической аппроксимации.
Pk
Px
Pk+1
Линейная интерполяция
55
56.
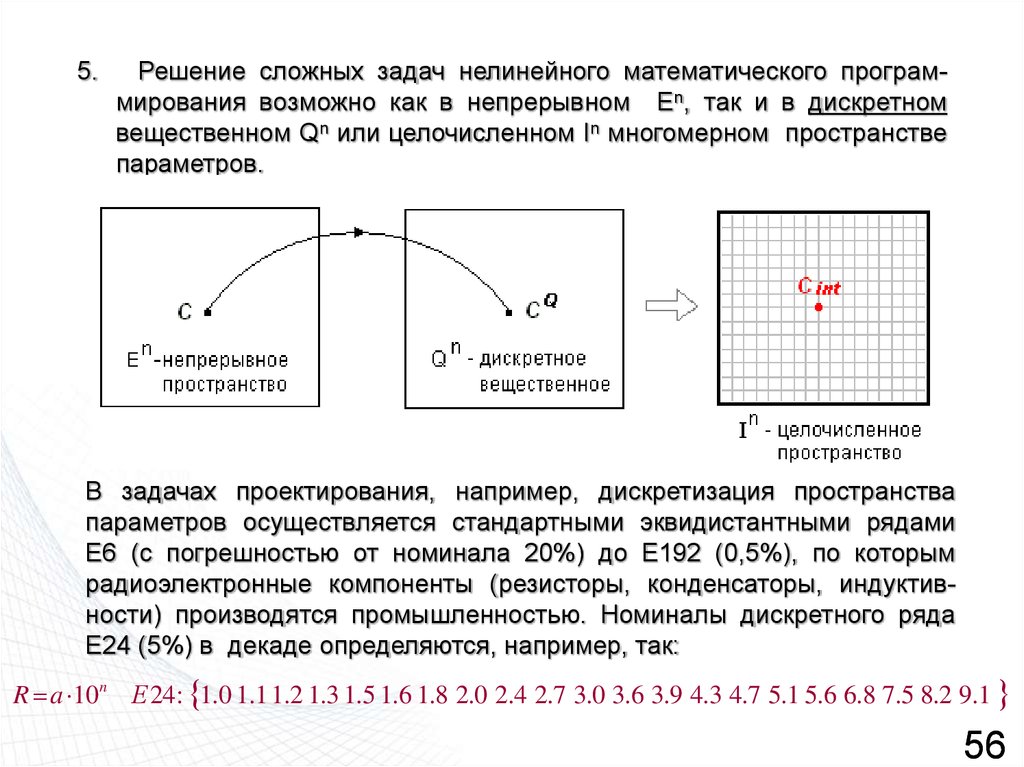
5.Решение сложных задач нелинейного математического программирования возможно как в непрерывном En, так и в дискретном
вещественном Qn или целочисленном In многомерном пространстве
параметров.
В задачах проектирования, например, дискретизация пространства
параметров осуществляется стандартными эквидистантными рядами
Е6 (с погрешностью от номинала 20%) до Е192 (0,5%), по которым
радиоэлектронные компоненты (резисторы, конденсаторы, индуктивности) производятся промышленностью. Номиналы дискретного ряда
Е24 (5%) в декаде определяются, например, так:
R a 10n Е 24: 1.0 1.1 1.2 1.3 1.5 1.6 1.8 2.0 2.4 2.7 3.0 3.6 3.9 4.3 4.7 5.1 5.6 6.8 7.5 8.2 9.1
56
57. Дискретный синтез активных фильтров гидроакустического тракта
58.
Структура гидроакустическойприемной станции
Гидрофон
Согласующее устройство
Основные задачи
1. Управление исполнительным
устройством по заданной команде
2. Задачи опознавания объектов по спектру
гидроакустических шумов
АРУ
Селектирующее устройство
Активный
фильтр
Цифровой
фильтр
Основные требования
1. Обеспечение совокупности
требуемых характеристик
2. Произвольная форма
характеристик
Блок цифровой
обработки
3. Линейность частотных шкал
4. Низкое энергопотребление
Блок принятия
решения
5. Устойчивость работы
6. Низкая стоимость
58
59.
Аналоговый трактДля обеспечения передачи информации по
гидроакустическому каналу на дистанции более
5 км используют частотный диапазон не выше
50 кГц. Приведем диапазоны шумов, которые
могут повлиять на работу устройства:
− динамические шумы (20 Гц
– 16 кГц);
− шумы мирового
судоходства, а также в гаванях и прибрежных
районах от технических сооружений (20 – 150
Гц);
− сейсмические шумы (0,1 –
25 Гц);
− подледные шумы (100 – 300
Гц, пики интенсивности на частотах 0,3 – 0,5 и
3 – 5 кГц);
− биологические шумы (63 Гц
– 200 кГц);
− тепловые шумы (на 50 кГц
порядка 8,9 мкПа).
Биологические шумы имеют обычно малую
интенсивность. Они могут помешать только
тогда, когда прибор находится в местах
массового скопления их источников, носящих
сезонный характер.
1, 2 – максимальные и
минимальные уровни
шумов
3 - шум при штиле по
Кнудсену
4 – сейсмические шумы
5 – шум горбылевых рыб
6 – шум креветок
7 – шум ливня
9 – шумы интенсивного
судоходства
С – шумы умеренного
судоходства
Гидрофонный тракт
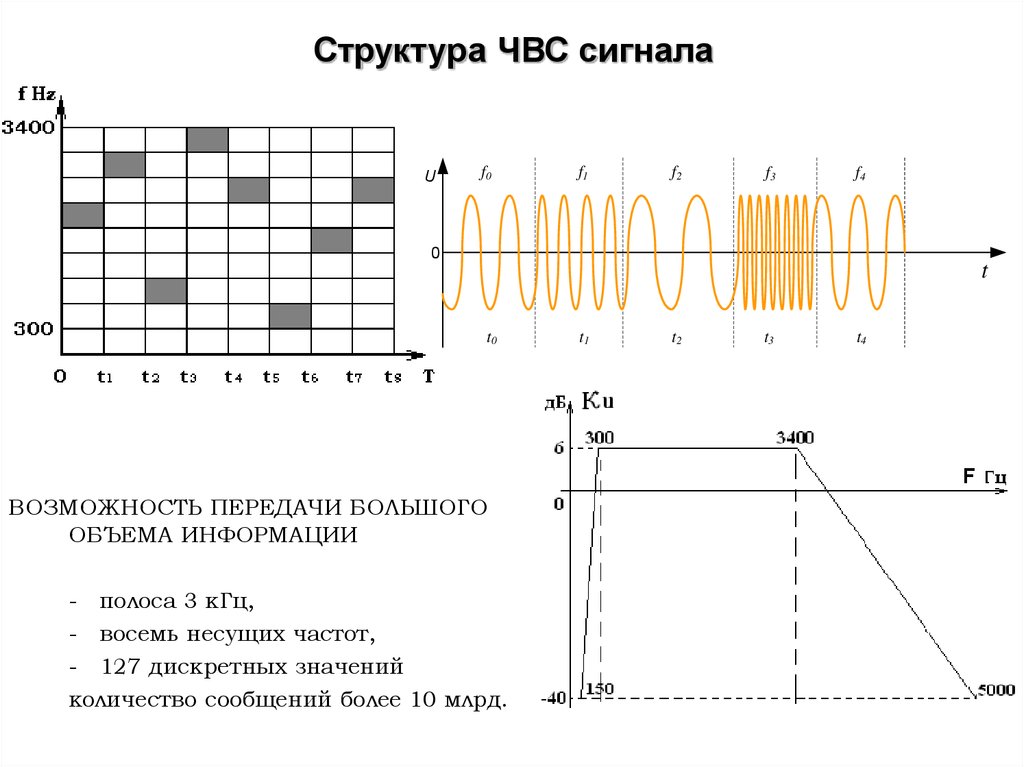
60. Структура ЧВС сигнала
Uf0
f1
f2
f3
f4
0
t
t0
ВОЗМОЖНОСТЬ ПЕРЕДАЧИ БОЛЬШОГО
ОБЪЕМА ИНФОРМАЦИИ
- полоса 3 кГц,
- восемь несущих частот,
- 127 дискретных значений
количество сообщений более 10 млрд.
t1
t2
t3
t4
61.
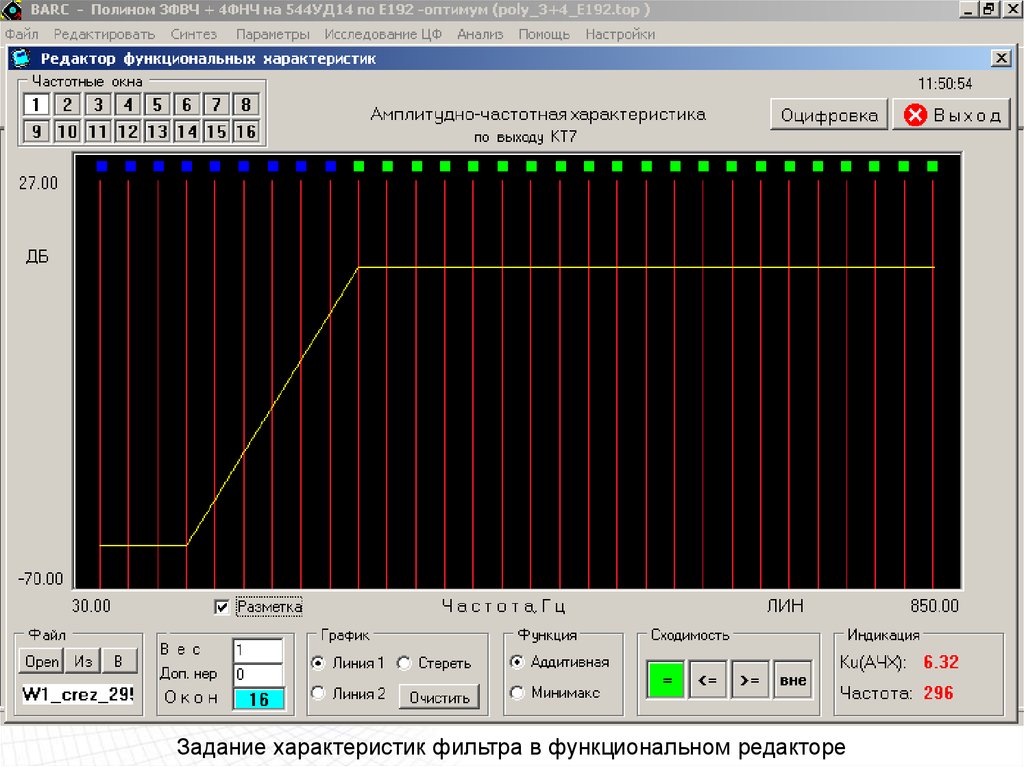
62. Техническое Задание Активный полосовой фильтр 300 – 3400 Гц
1. Полоса пропускания 300 – 3400 Гц2. Усиление в полосе 6 0.5 дБ
3. Затухание на 150 Гц
не менее –40 дБ
4. Затухание на 5 кГц
не менее –40 дБ
5. Фазовые искажение не более 60
градусов в полосе 300 – 3400 Гц
6. Дискретизация варьируемых
параметров по ряду Е192
7. Компонентные ограничения
Смах = 44.2 нФ
Смin = 36 пФ
62
63. Выбор схемы каскадов фильтра
Одноконтурная обратная связьСхема с инвертором проводимостей
Схема на источнике напряжения,
управляемом напряжением
Многопетлевая обратная связь
63
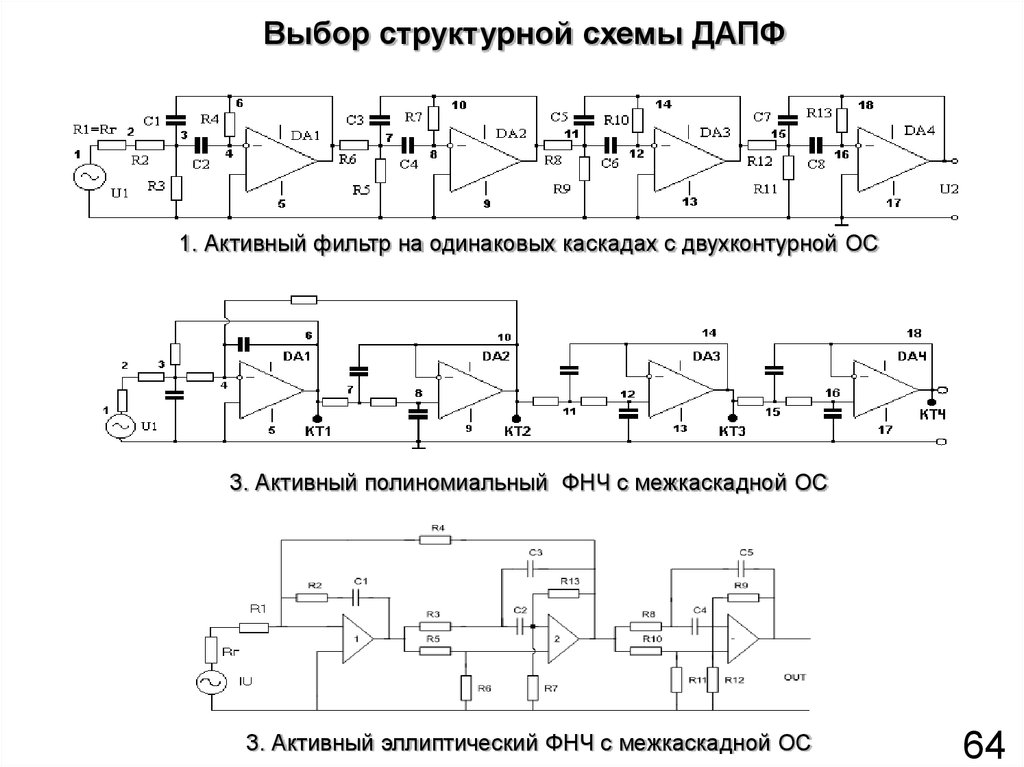
64. Выбор структурной схемы ДАПФ
1. Активный фильтр на одинаковых каскадах с двухконтурной ОС3. Активный полиномиальный ФНЧ с межкаскадной ОС
3. Активный эллиптический ФНЧ с межкаскадной ОС
64
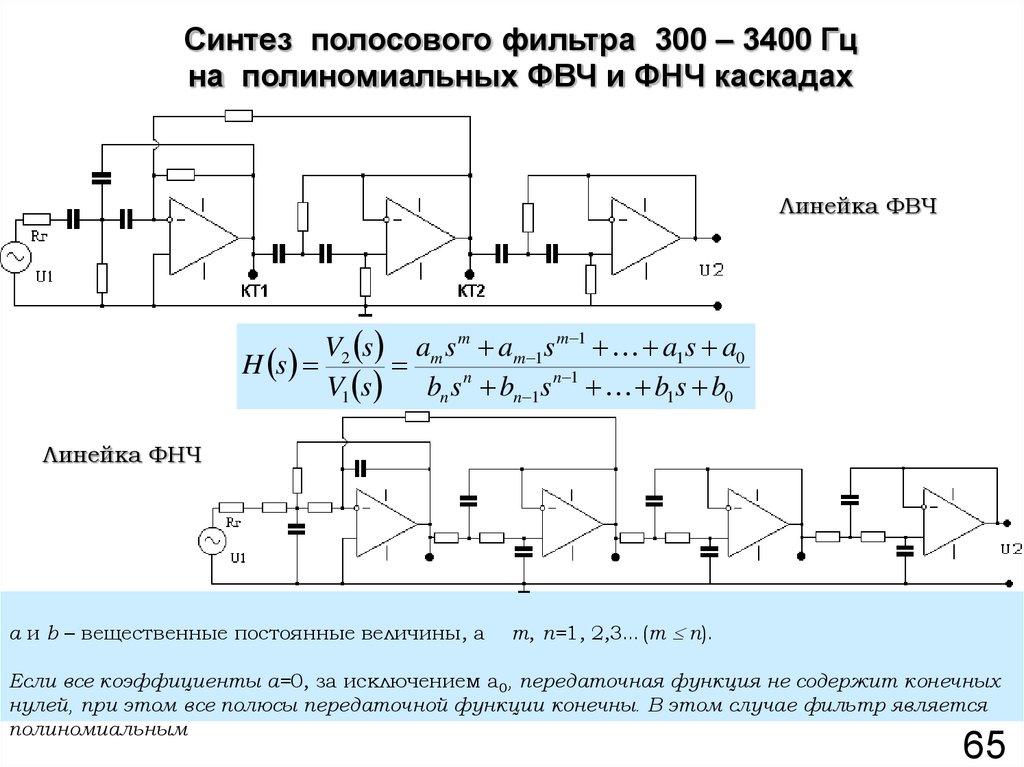
65. Синтез полосового фильтра 300 – 3400 Гц на полиномиальных ФВЧ и ФНЧ каскадах
Линейка ФВЧV2 s am s m am 1s m 1 a1s a0
H s
V1 s
bn s n bn 1s n 1 b1s b0
Линейка ФНЧ
a и b – вещественные постоянные величины, а
m, n=1, 2,3…(m n).
Если все коэффициенты a=0, за исключением а0, передаточная функция не содержит конечных
нулей, при этом все полюсы передаточной функции конечны. В этом случае фильтр является
полиномиальным
65
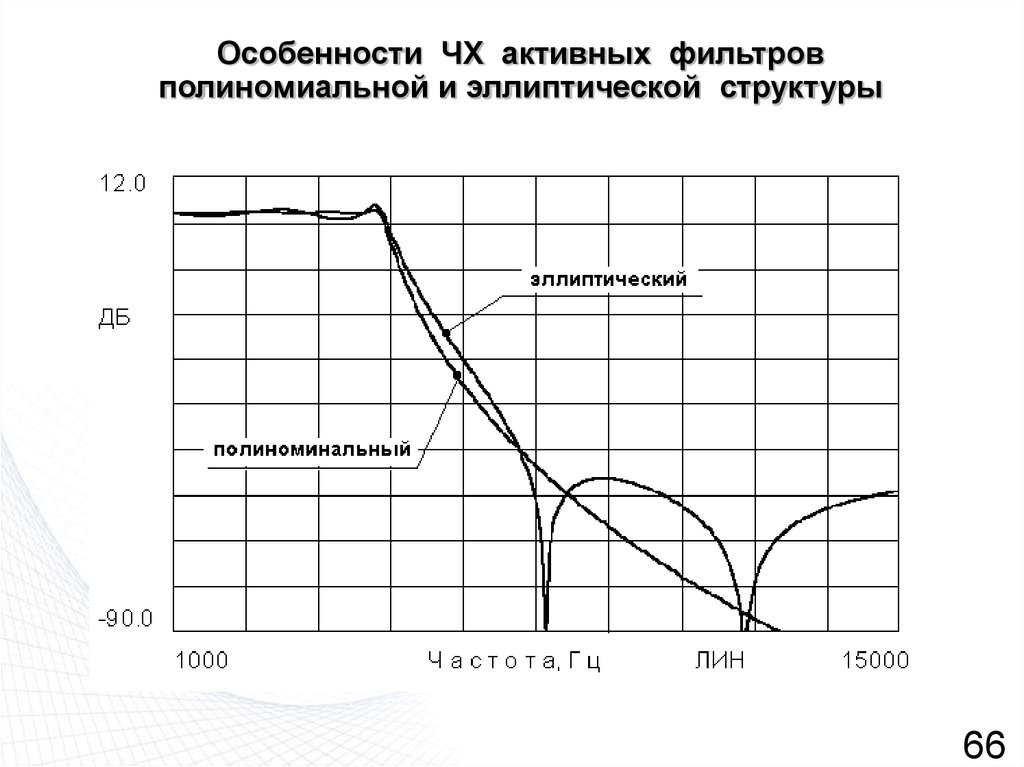
66. Особенности ЧХ активных фильтров полиномиальной и эллиптической структуры
6667. Выбор структурной схемы
Ветвей 83Узлов 30
67
68. Выбор операционного усилителя
Название
Производите
ль
Ток потребления
Питан
ие
Полоса (по 0 Дб)
MCP6144
600 нА
± 3,5 В
5 кГц
4
AD8132
7,25 мА
± 5.5 В
400 МГц
2
544 уд 14
1,7 мА
± 7,5 В
1МГц
4
МАХ4254
1,5 мА
± 2,5 В
2 МГц
4
ПРИМЕНЕНИЯ
• Многокаскадные схемы с высоким входным сопротивлением и повышенным
быстродействием
• Преобразователи тока в напряжение, в том числе для ЦАП
• Инструментальные усилители
• Схемы активных фильтров
Штук в
корпусе
68
69.
Основные характеристики:Входное сопротивление –
1012Ом
Входная емкость – 7 пФ
Выходное сопротивление (без
ОС) – 150 Ом
Питание VDD VSS - ± 7,5 В
(7,5±2,5)
70. Однополюсные макромодели операционных усилителей
графикБоде
U 2K
S K RK
U 1K 1 pC K R K
f Пк
1
RК C К
Звено, моделирующее k-ый полюс передаточной функции ОУ
70
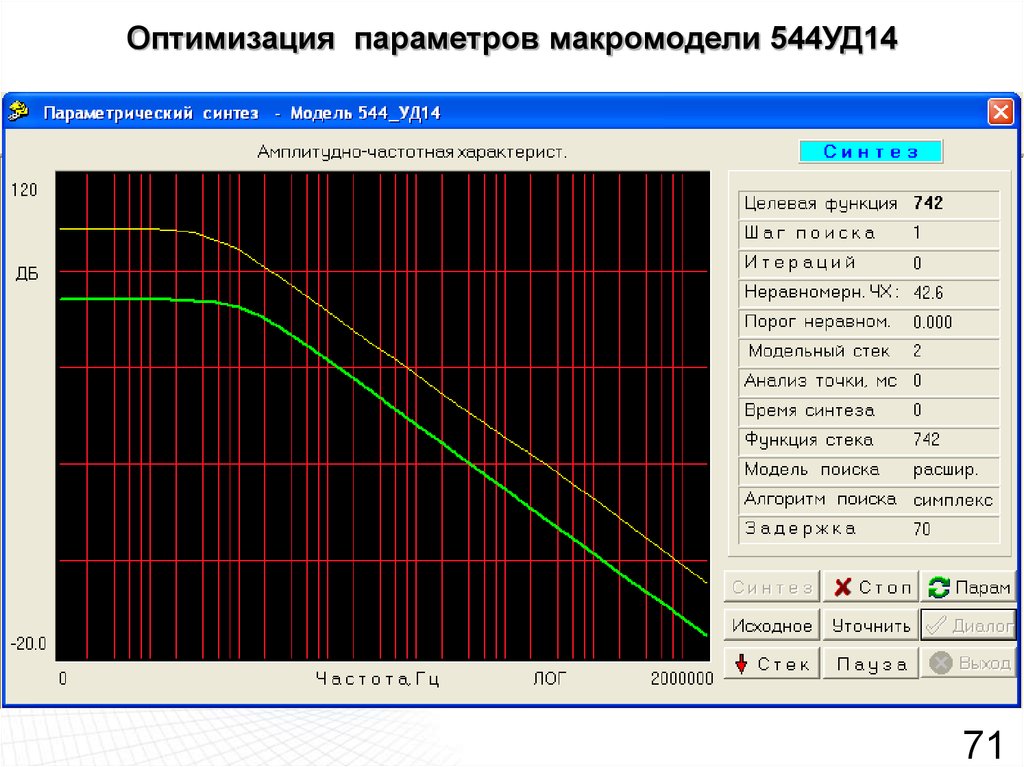
71. Оптимизация параметров макромодели 544УД14
7172. Оптимизация параметров макромодели 544УД14
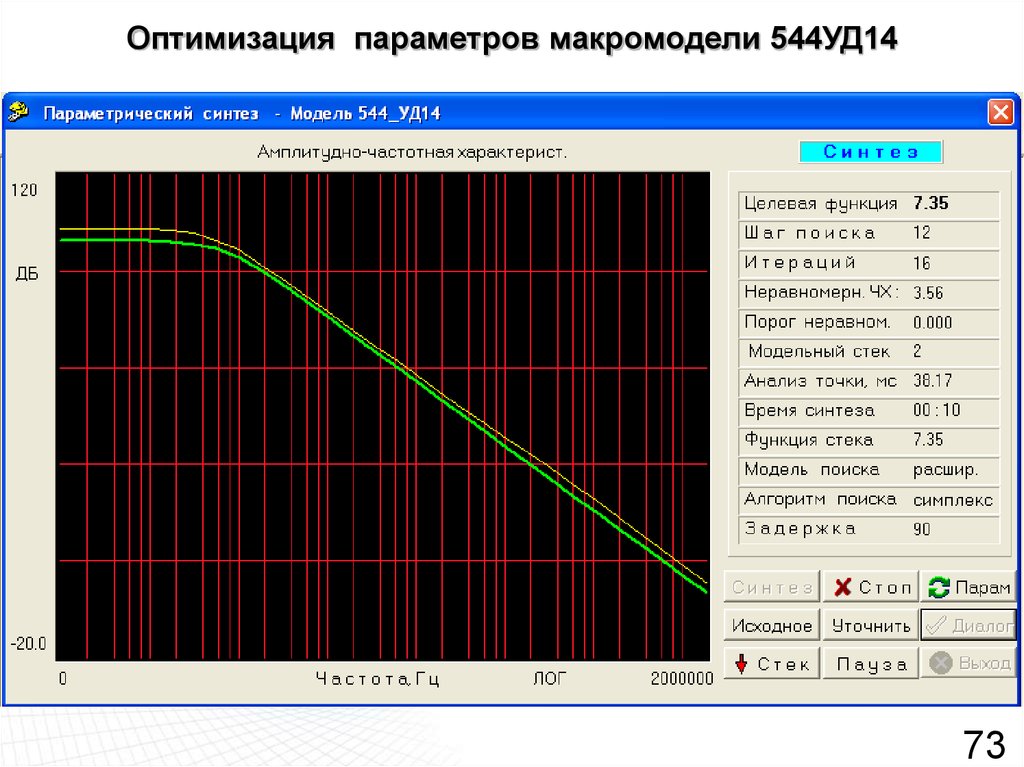
7273. Оптимизация параметров макромодели 544УД14
7374. Оптимизация параметров макромодели 544УД14
7475. Оптимизация параметров макромодели 544УД14
7576. Постановка задачи многофункционального дискретного синтеза активного фильтра
F(XD) β w fw (XD) (1)w
o
o
F( XD) min F(XD)
(2)
XD Sn Е 192
10 Ом Ri 1 МОм
36 пФ Ci 44.2 нФ
Kj K
max
j
(3)
где: ХDО - вектор оптимальных дискретных параметров фильтра,
ХD - текущий вектор варьируемых дискретных параметров,
Sn - область изменения дискретных варьируемых параметров.
Кmax - предельно-допустимое усиление каскада
Дискретизация пространства параметров Sn осуществляется по
стандартным рядам
Е6 - Е192
(ГОСТ 2852-67).
Номиналы
определяются по формуле
R a 10n Е 24: 1.0 1.1 1.2 1.3 1.5 1.6 1.8 2.0 2.4 2.7 3.0 3.6 3.9 4.3 4.7 5.1 5.6 6.8 7.5 8.2 9.1
76
77. Формирование частных целевых функций
Частные целевых функций fi(XD) отвечают за i-уючастотную
характеристику фильтра и формируются в функциональном редакторе пакета
в среднеквадратичном либо минимаксном виде
F(XD) β1f1 (XD) β 2 f 2 (XD) ... β n f n (XD)
1 p
f i (XD) Yk (XD) YkT
p k 1
Yj (XD) Y
k j (XD)
T
Y
j
T
j
p
1
f i (XD)
p k 1
ΔYj k j YjT
Yk (XD) Y
T
Y
k
T
k
f i (XD) maх | Yk (XD) YkT |2
k
(4)
2
Минимаксный критерий
2
- погрешность
синтеза
2
(5)
(6)
77
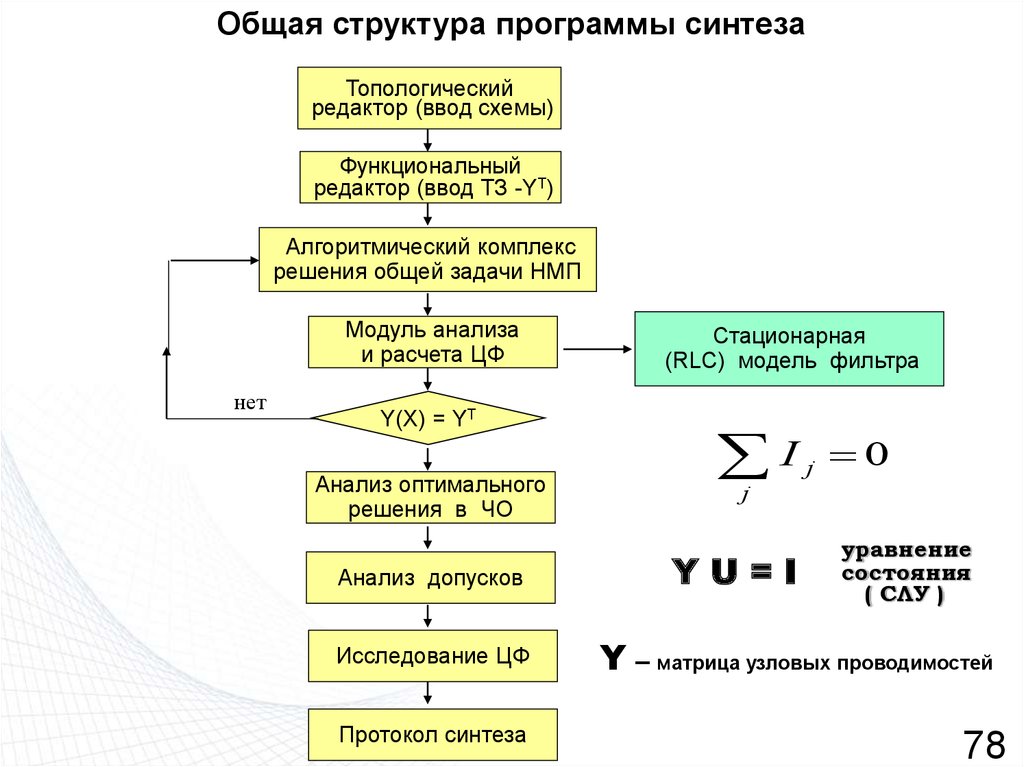
78. Общая структура программы синтеза
Топологическийредактор (ввод схемы)
Функциональный
редактор (ввод ТЗ -YT)
Алгоритмический комплекс
решения общей задачи НМП
Модуль анализа
и расчета ЦФ
нет
Y(X) = YT
Анализ оптимального
решения в ЧО
Анализ допусков
Исследование ЦФ
Протокол синтеза
Стационарная
(RLC) модель фильтра
I
j
0
j
YU=I
уравнение
состояния
( СЛУ )
Y – матрица узловых проводимостей
78
79.
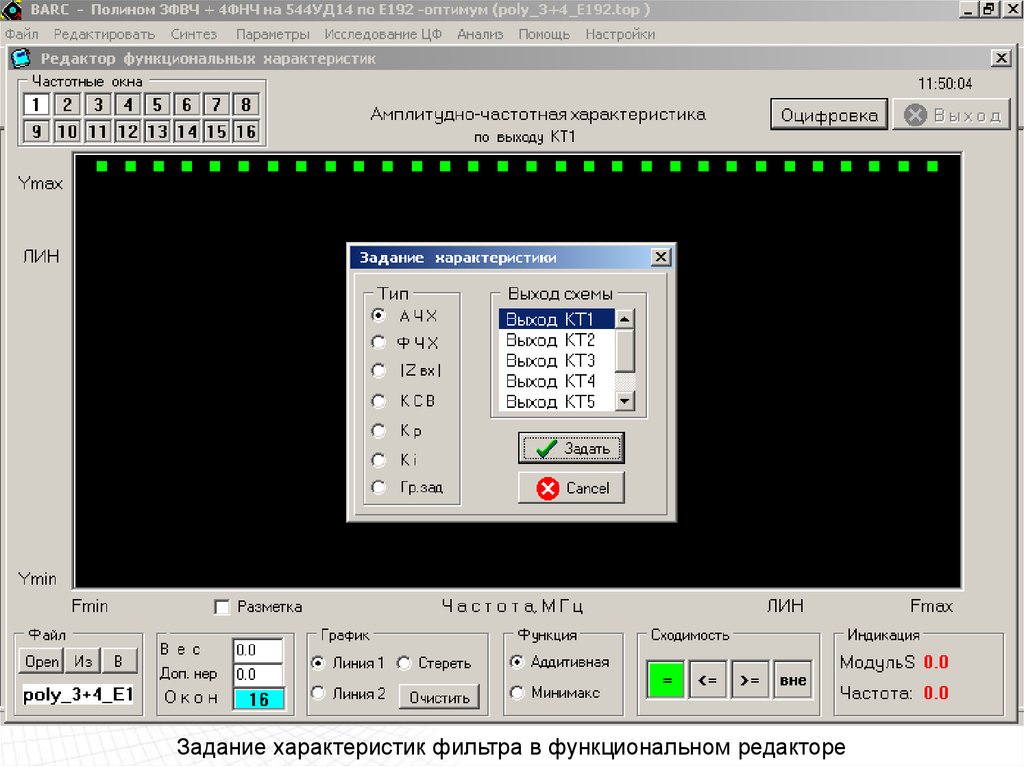
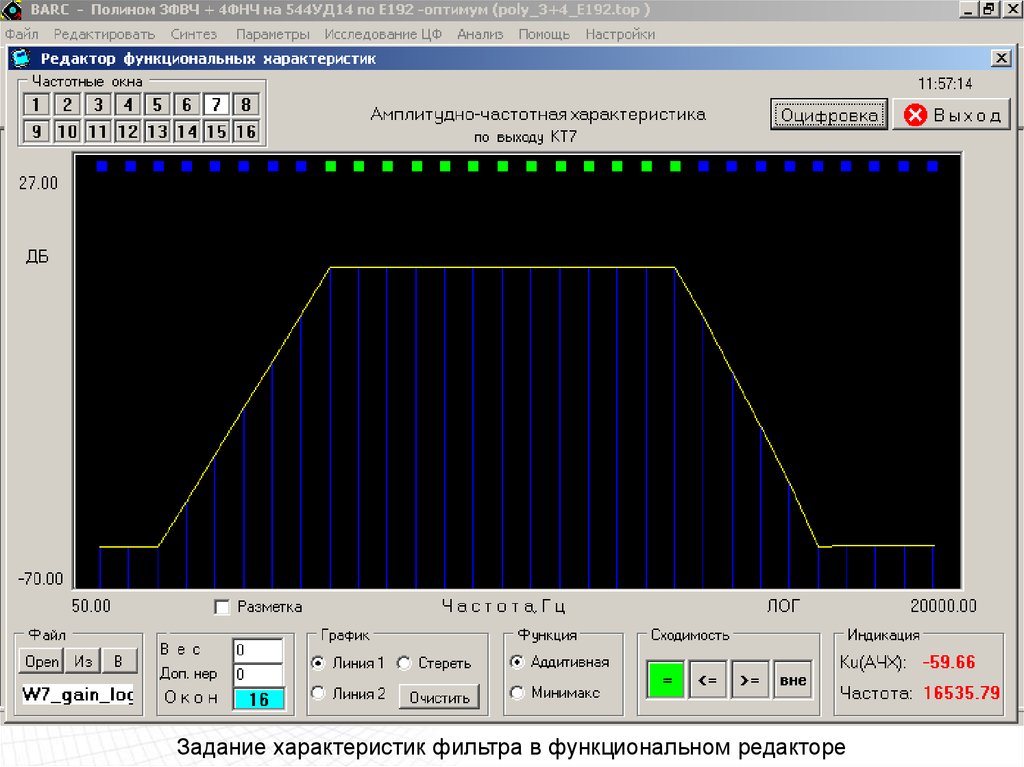
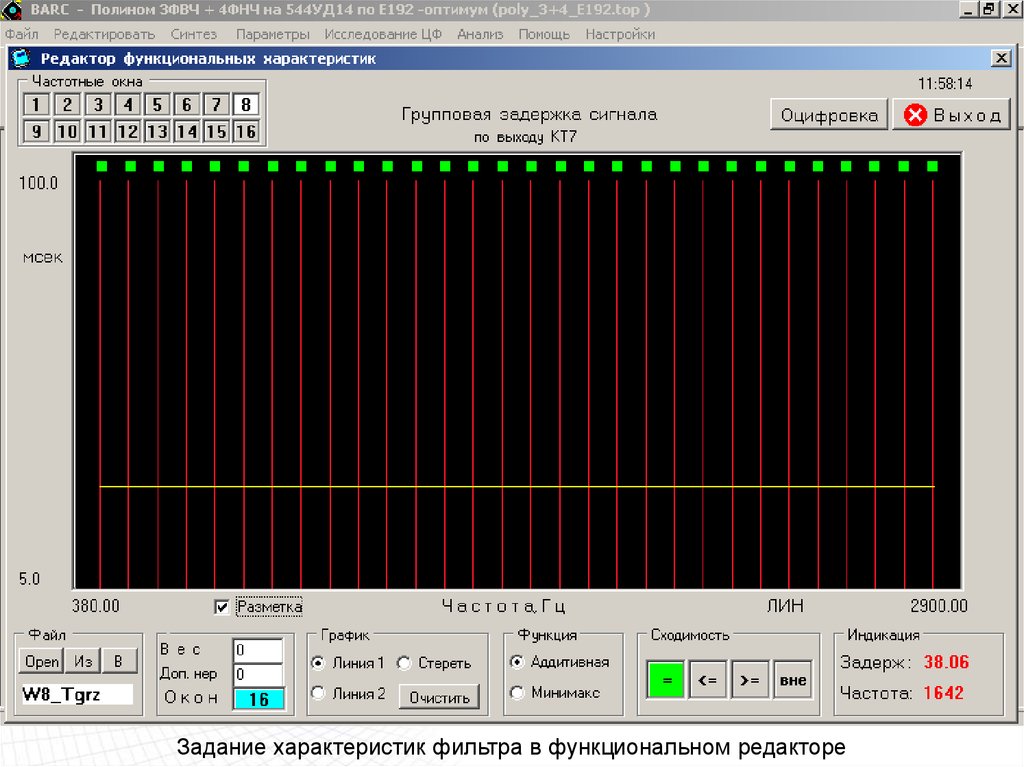
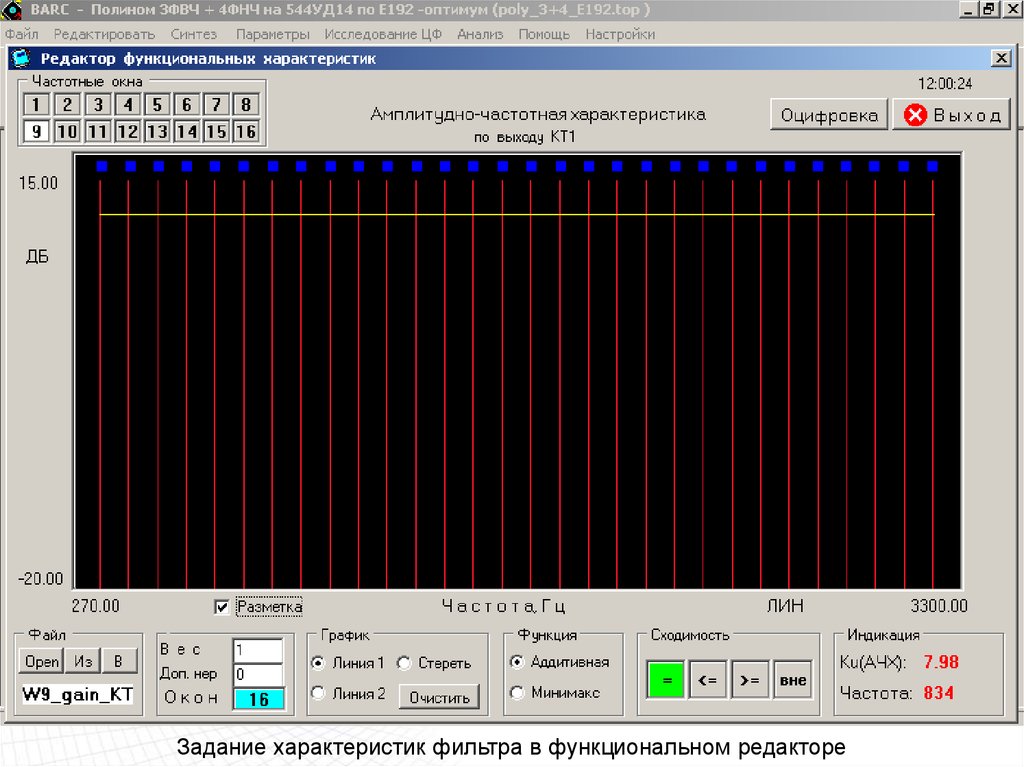
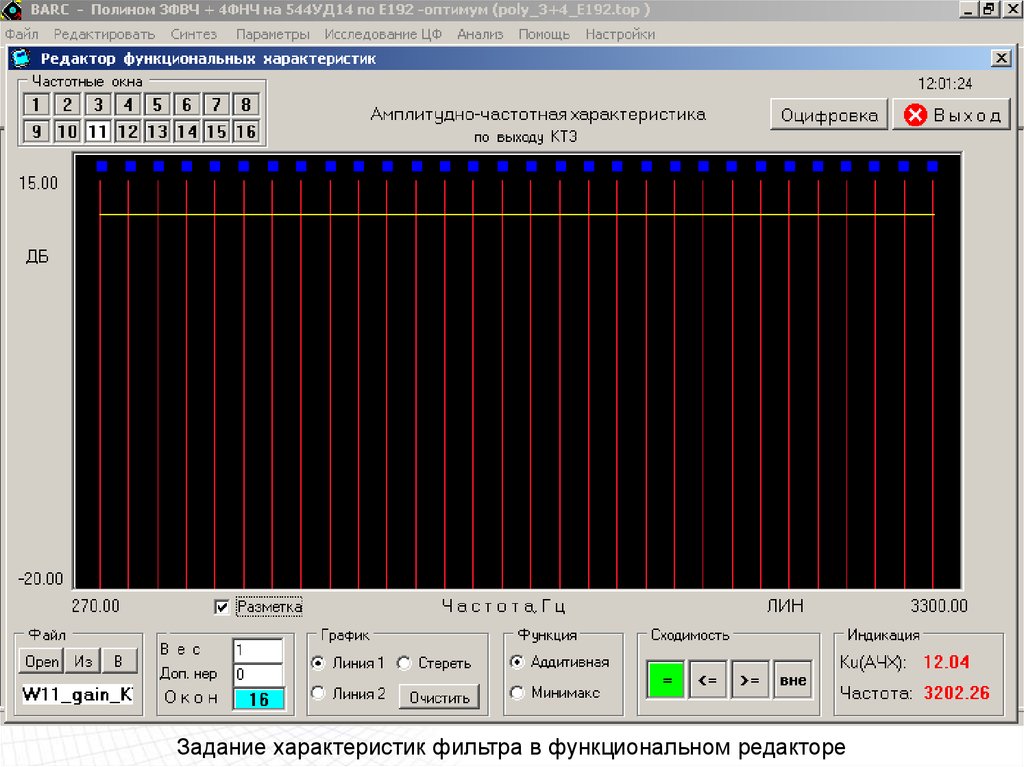
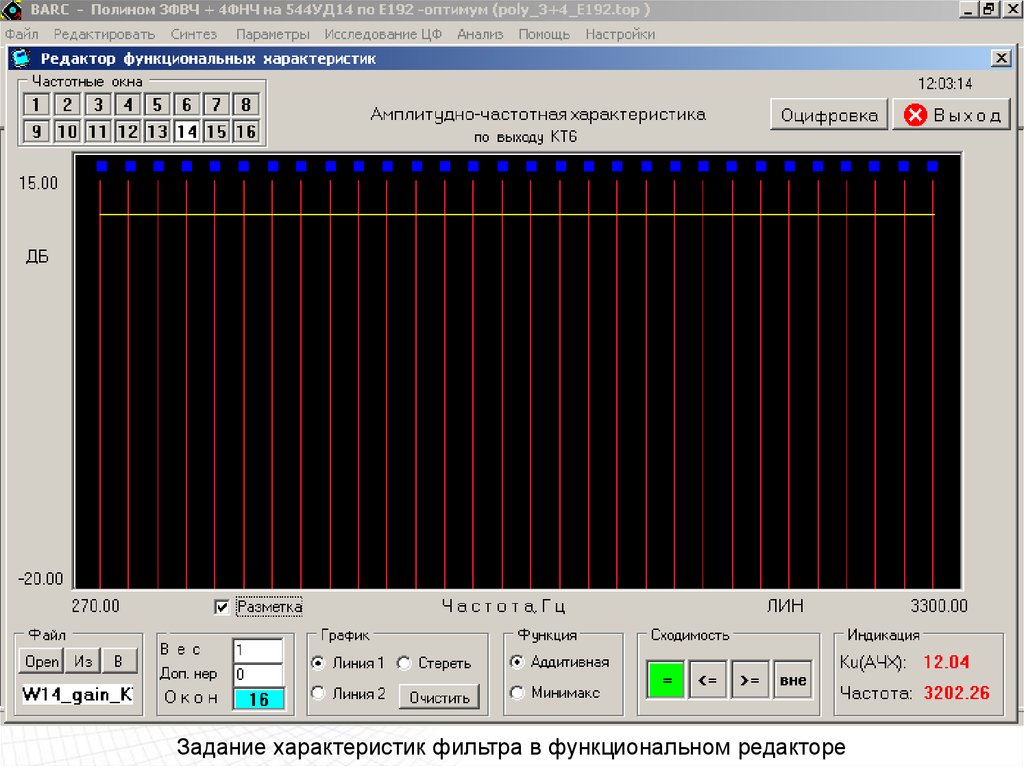
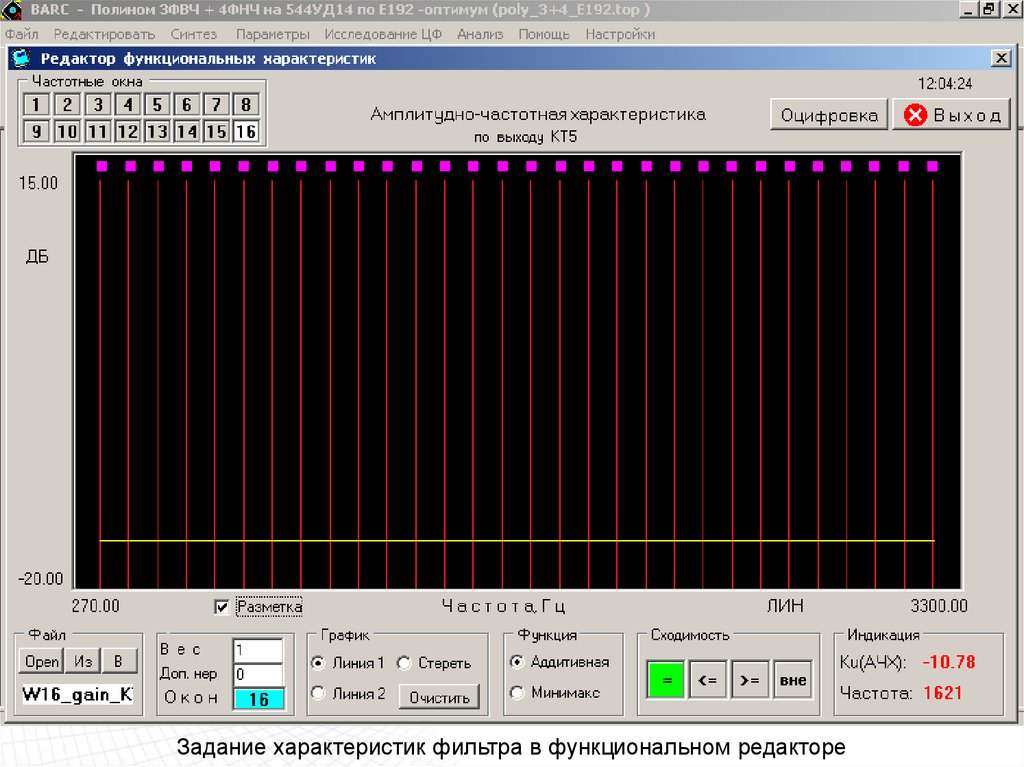
Задание характеристик фильтра в функциональном редакторе80.
Задание характеристик фильтра в функциональном редакторе81.
Задание характеристик фильтра в функциональном редакторе82.
Задание характеристик фильтра в функциональном редакторе83.
Задание характеристик фильтра в функциональном редакторе84.
Задание характеристик фильтра в функциональном редакторе85.
Задание характеристик фильтра в функциональном редакторе86.
Задание характеристик фильтра в функциональном редакторе87.
Задание характеристик фильтра в функциональном редакторе88.
Задание характеристик фильтра в функциональном редакторе89.
Задание характеристик фильтра в функциональном редакторе90.
Задание характеристик фильтра в функциональном редакторе91.
Задание характеристик фильтра в функциональном редакторе92.
Задание характеристик фильтра в функциональном редакторе93.
Задание характеристик фильтра в функциональном редакторе94.
Задание характеристик фильтра в функциональном редакторе95.
Задание характеристик фильтра в функциональном редакторе96.
Начальные значения дискретных параметров фильтра97.
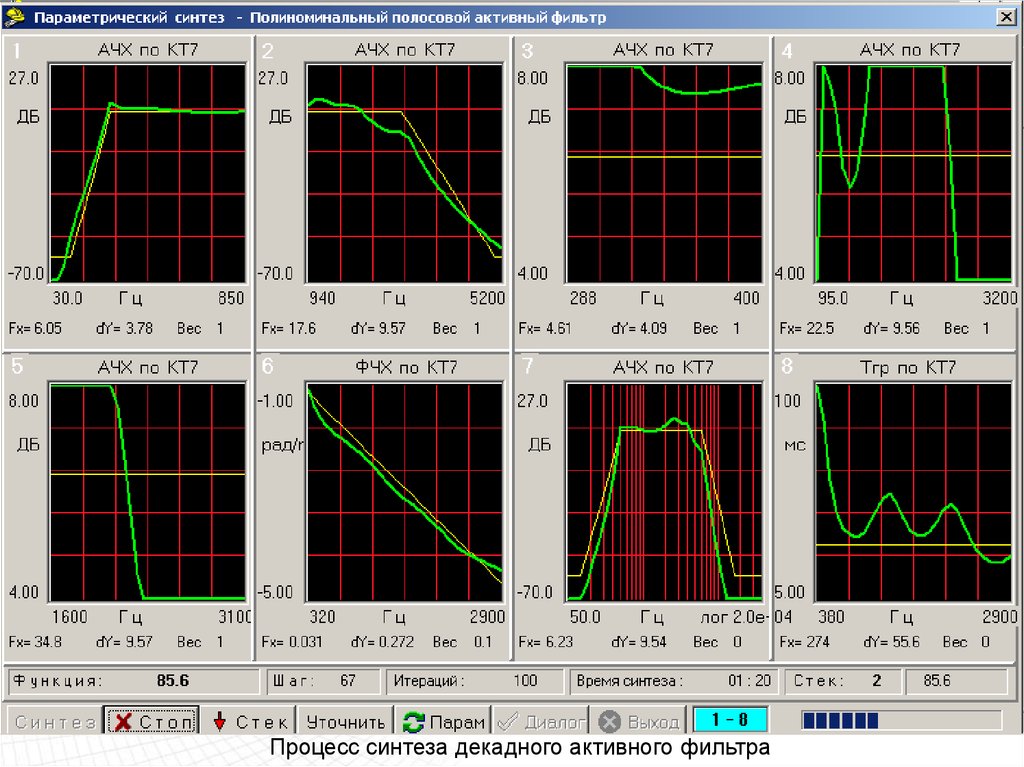
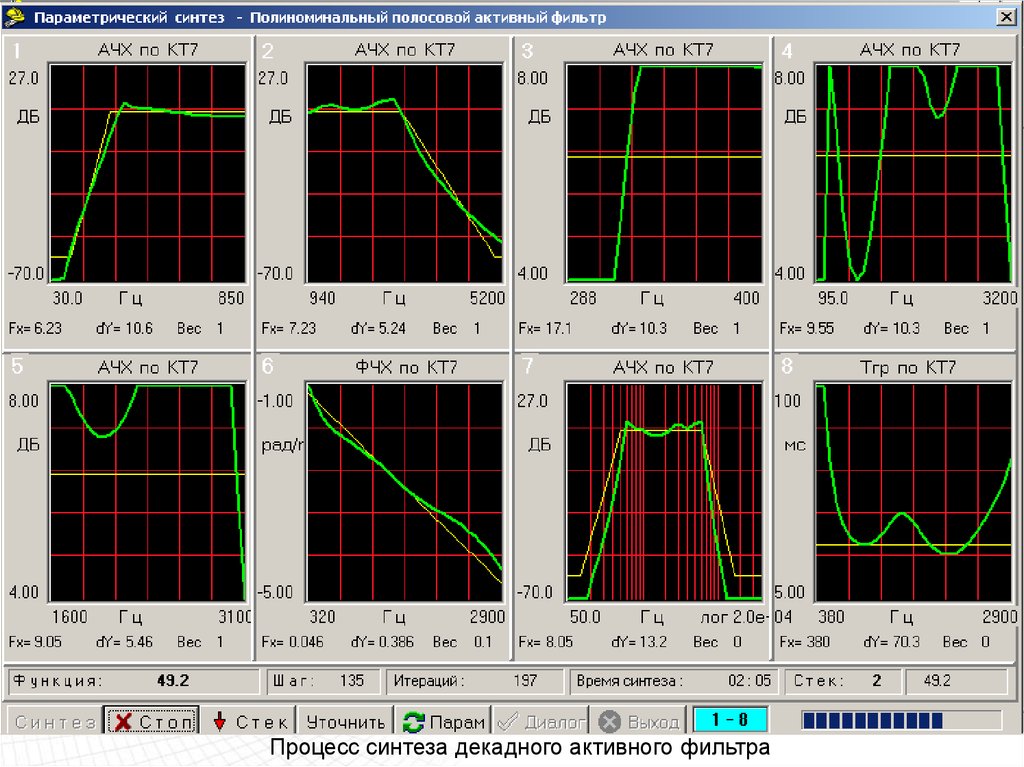
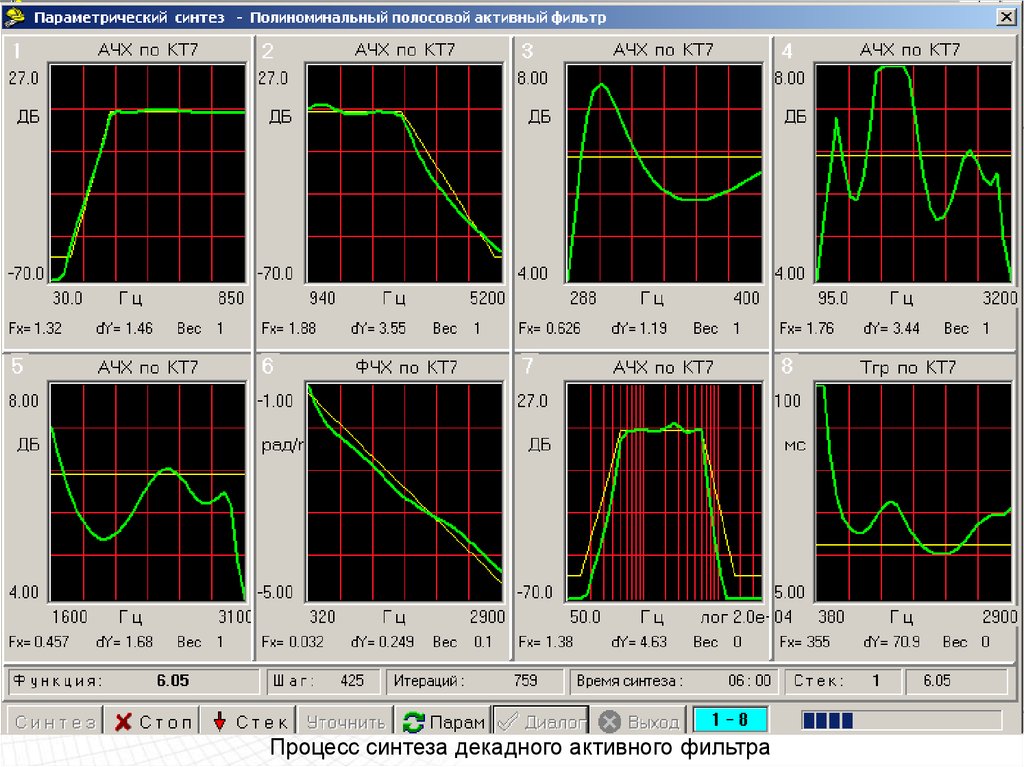
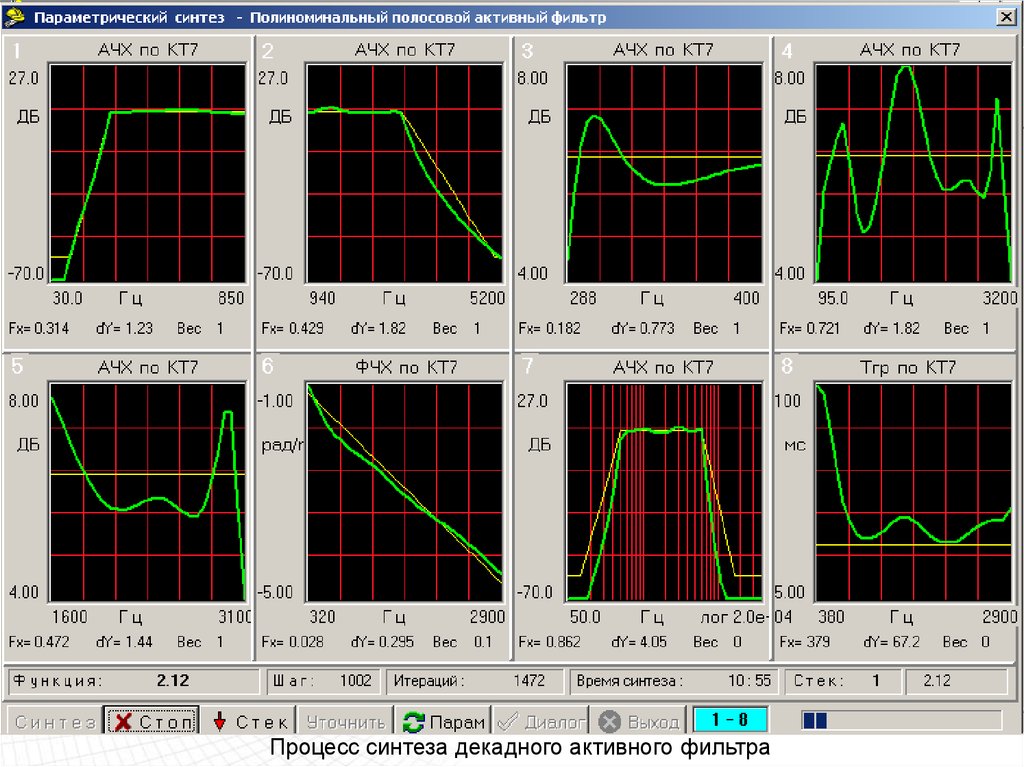
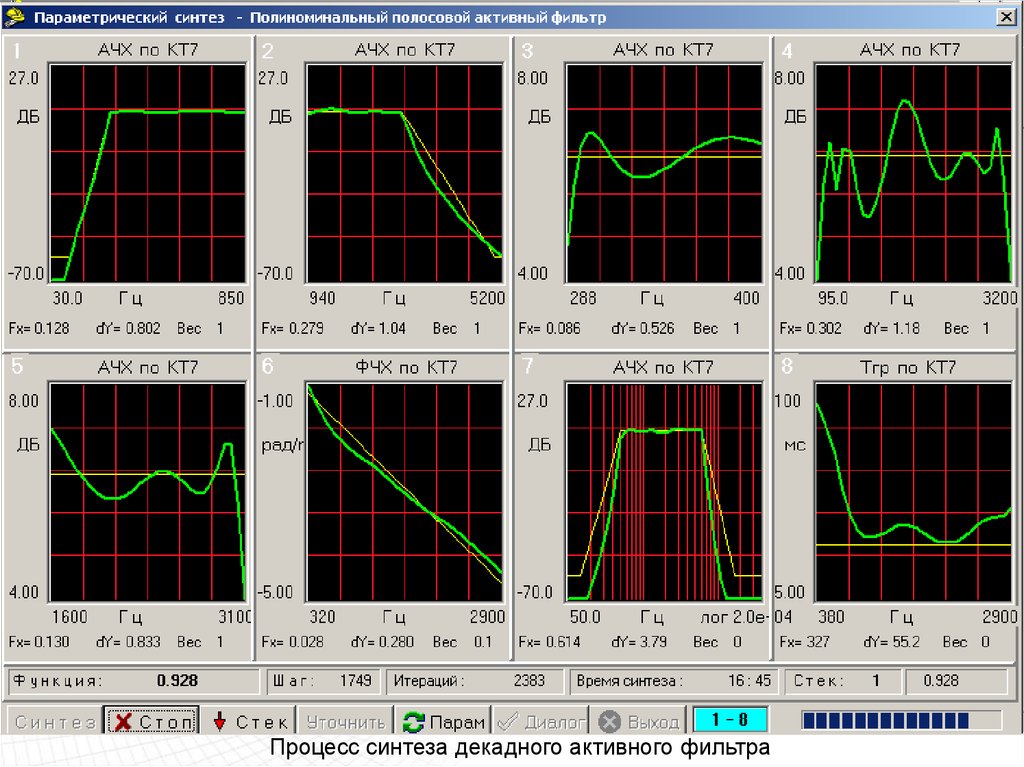
Процесс синтеза декадного активного фильтра98.
Процесс синтеза декадного активного фильтра99.
Процесс синтеза декадного активного фильтра100.
Процесс синтеза декадного активного фильтра101.
Процесс синтеза декадного активного фильтра102.
Процесс синтеза декадного активного фильтра103.
Процесс синтеза декадного активного фильтра104.
Процесс синтеза декадного активного фильтра105.
Процесс синтеза декадного активного фильтра106.
Процесс синтеза декадного активного фильтра107.
Процесс синтеза декадного активного фильтра108.
Синтез декадного активного фильтра завершен109.
Синтез декадного активного фильтра завершен110.
Профиль разреза целевого функционала110
111.
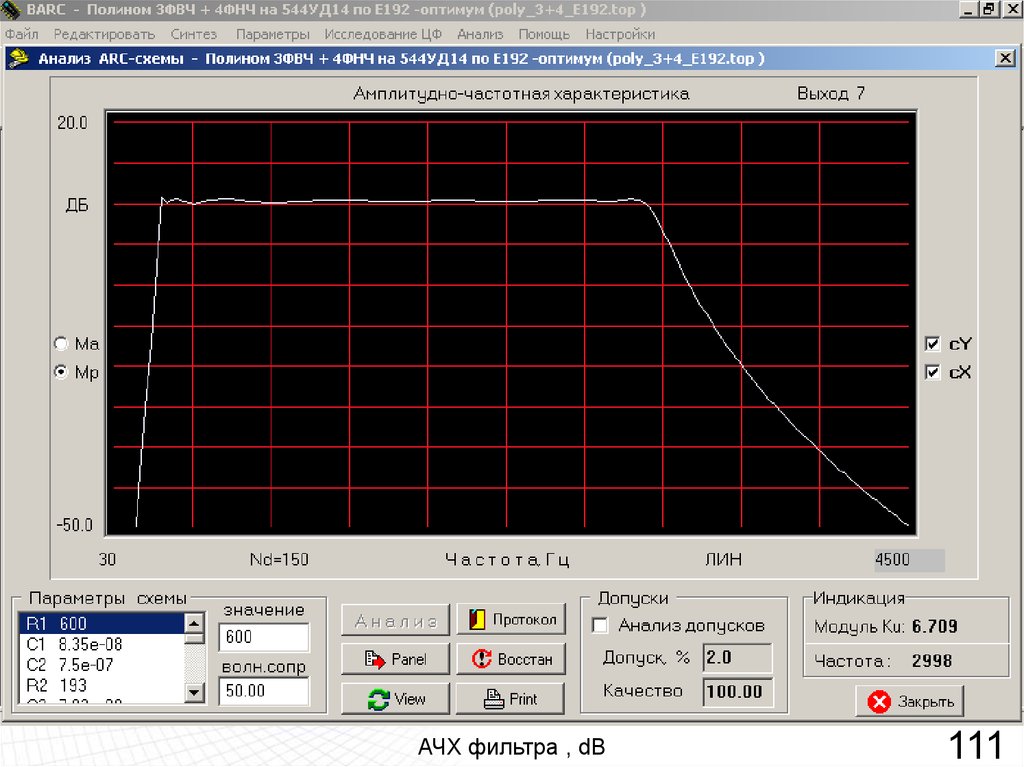
АЧХ фильтра , dB111
112.
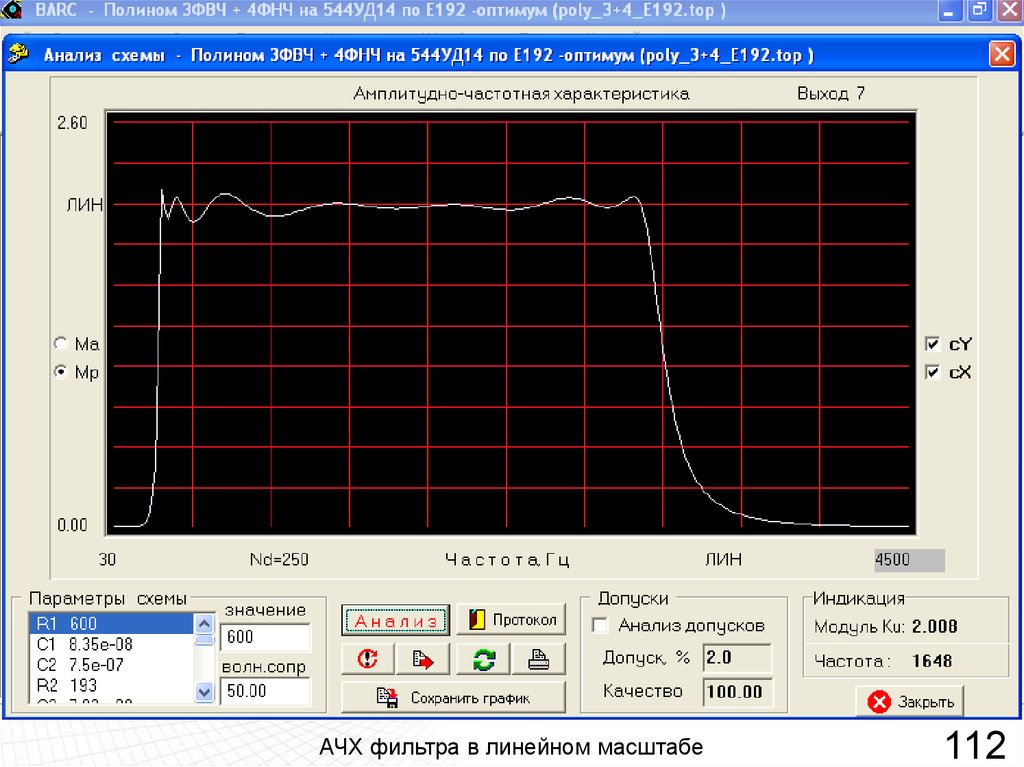
АЧХ фильтра в линейном масштабе112
113.
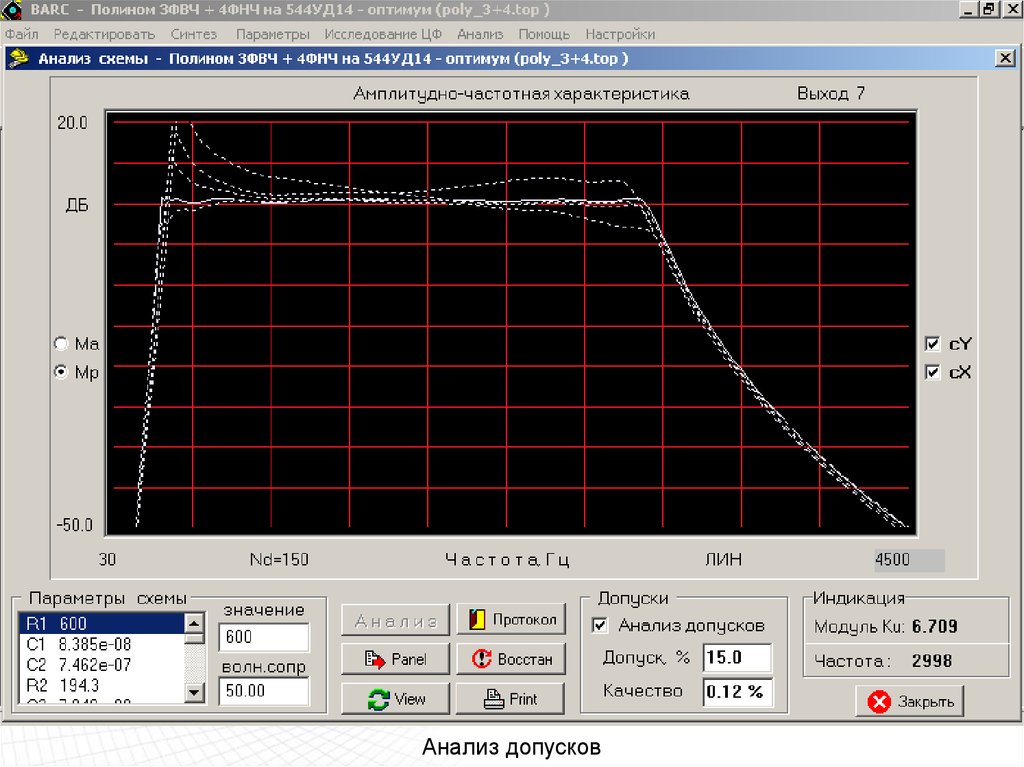
Анализ допусков114.
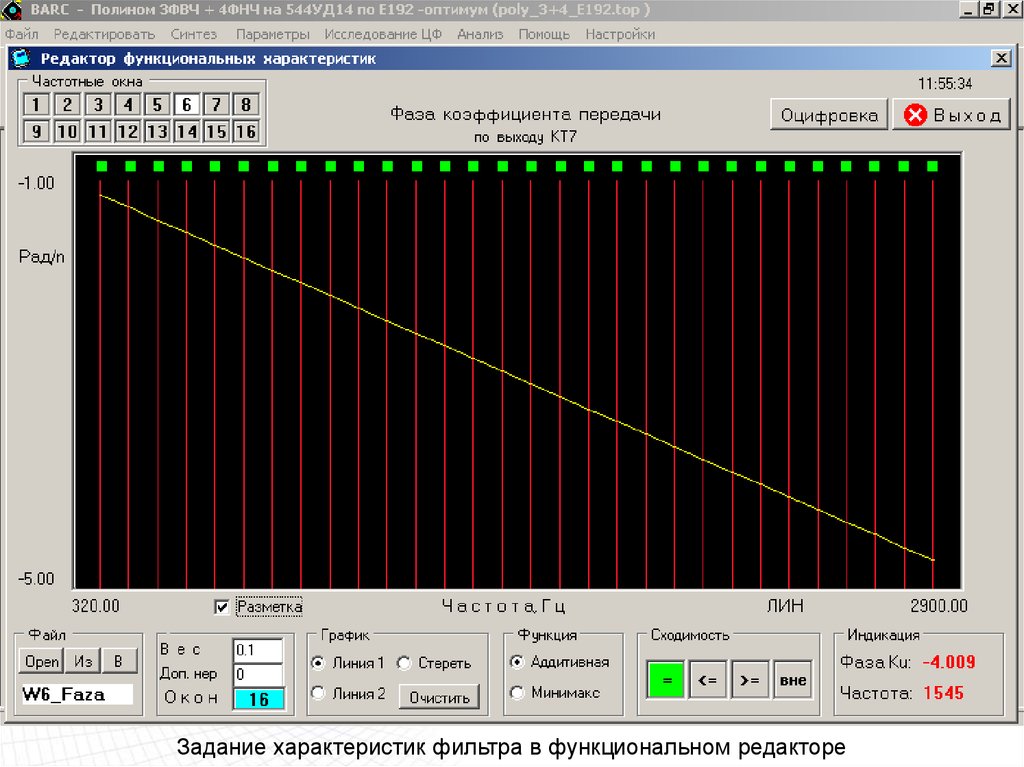
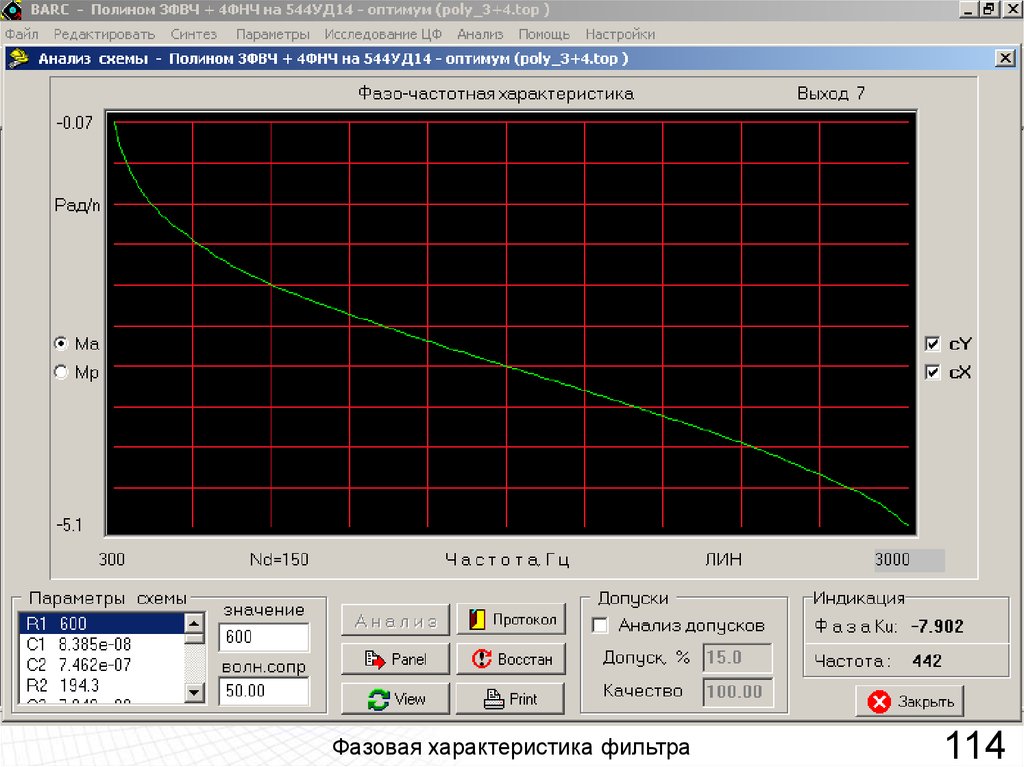
Фазовая характеристика фильтра114
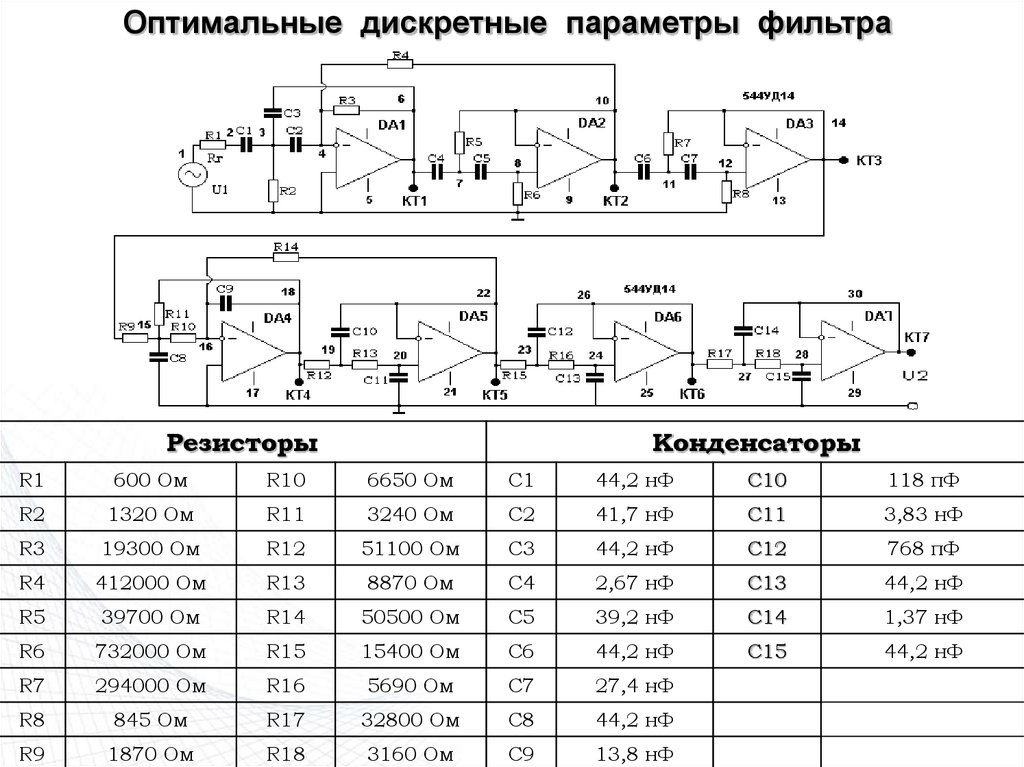
115. Оптимальные дискретные параметры фильтра
РезисторыКонденсаторы
R1
600 Ом
R10
6650 Ом
C1
44,2 нФ
C10
118 пФ
R2
1320 Ом
R11
3240 Ом
C2
41,7 нФ
C11
3,83 нФ
R3
19300 Ом
R12
51100 Oм
C3
44,2 нФ
C12
768 пФ
R4
412000 Ом
R13
8870 Ом
C4
2,67 нФ
C13
44,2 нФ
R5
39700 Ом
R14
50500 Ом
C5
39,2 нФ
C14
1,37 нФ
R6
732000 Ом
R15
15400 Ом
C6
44,2 нФ
C15
44,2 нФ
R7
294000 Ом
R16
5690 Ом
C7
27,4 нФ
R8
845 Ом
R17
32800 Ом
С8
44,2 нФ
R9
1870 Ом
R18
3160 Ом
C9
13,8 нФ
116.
Вид фильтра на макетной плате116
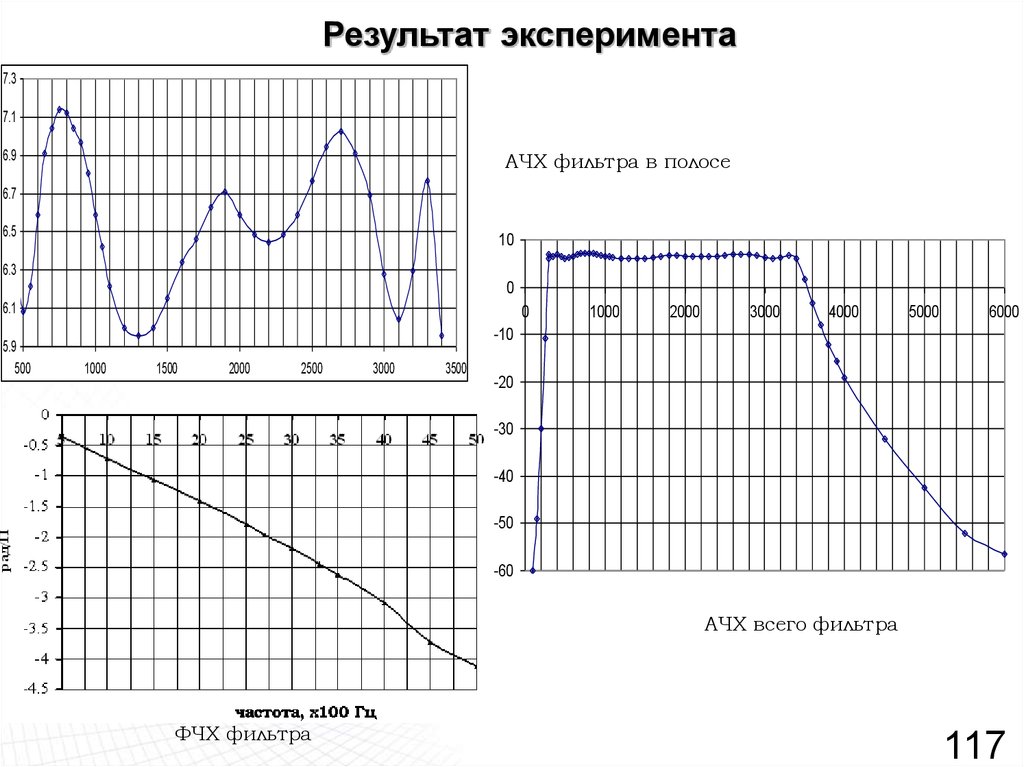
117. Результат эксперимента
7.37.1
6.9
АЧХ фильтра в полосе
6.7
6.5
10
6.3
0
6.1
5.9
500
0
1000
2000
3000
4000
5000
6000
-10
1000
1500
2000
2500
3000
3500
-20
-30
-40
-50
-60
АЧХ всего фильтра
ФЧХ фильтра
117
118.
Вид фильтра в составе изделия «Весть»118
119. Техническое задание, результаты синтеза на ЭВМ и экспериментальные данные
Техническоезадание
Синтез
на ЭВМ
Эксперимент
300 - 3400
294 - 3455
290 - 3410
2. Усиление в полосе, дБ
6-7
6,4
6,3
3. Неравномерность , дБ
0,5
0,46
0,67
4. Затухание на 150 Гц, дБ
40
58
46
5. Затухание на 5 кГц, дБ
40
56
43
6.Фазовые искажения, Град
60
51,6
57
Показатели фильтра
1. Диапазон частот, Гц
119
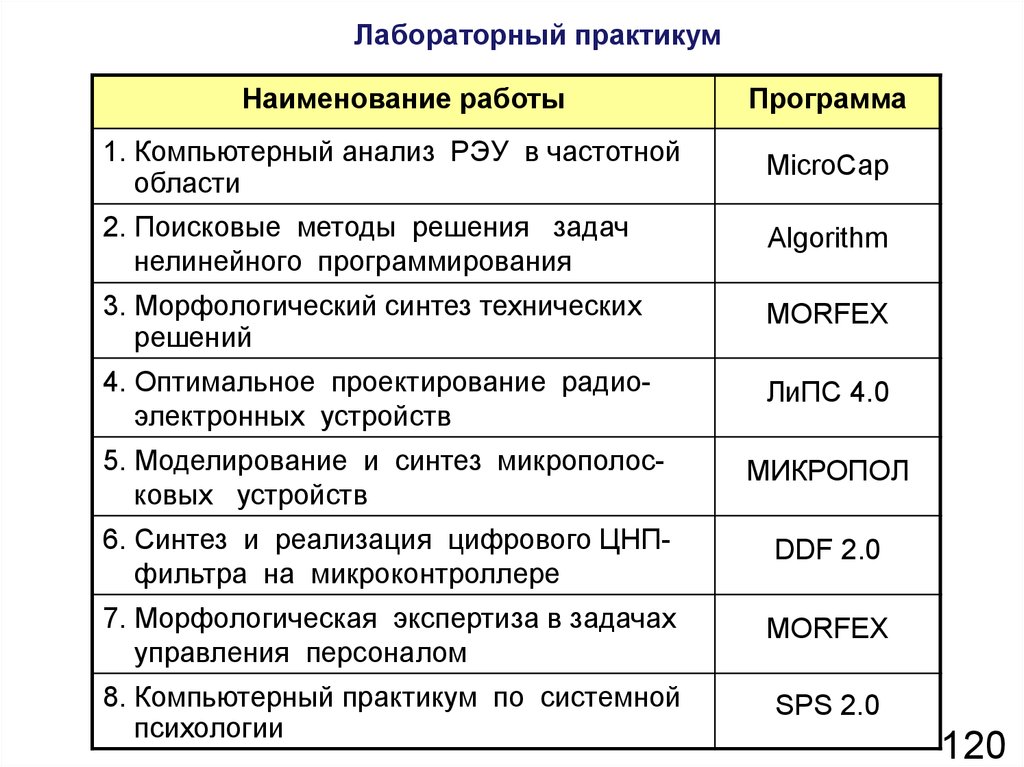
120. Лабораторный практикум
Наименование работыПрограмма
1. Компьютерный анализ РЭУ в частотной
области
MicroCap
2. Поисковые методы решения задач
нелинейного программирования
Algorithm
3. Морфологический синтез технических
решений
MORFEX
4. Оптимальное проектирование радиоэлектронных устройств
ЛиПС 4.0
5. Моделирование и синтез микрополосковых устройств
МИКРОПОЛ
6. Синтез и реализация цифрового ЦНПфильтра на микроконтроллере
DDF 2.0
7. Морфологическая экспертиза в задачах
управления персоналом
MORFEX
8. Компьютерный практикум по системной
психологии
SPS 2.0
120














































































 mathematics
mathematics electronics
electronics








