Движение в геометрии

1.

26.03.2019
ДВИЖЕНИЯ

2.

ДВИЖЕНИЕ – преобразование фигуры F в фигуру F1
СВОЙСТВА ДВИЖЕНИЯ:
1.Точки, лежащие на прямой, переходят в
точки, лежащие на прямой.
2. Прямые переходят в прямые, полупрямые –
в полупрямые, от резки – в от резки.
3. Сохраняют ся углы между полупрямыми.
4. Плоскост ь переходит в плоскост ь.

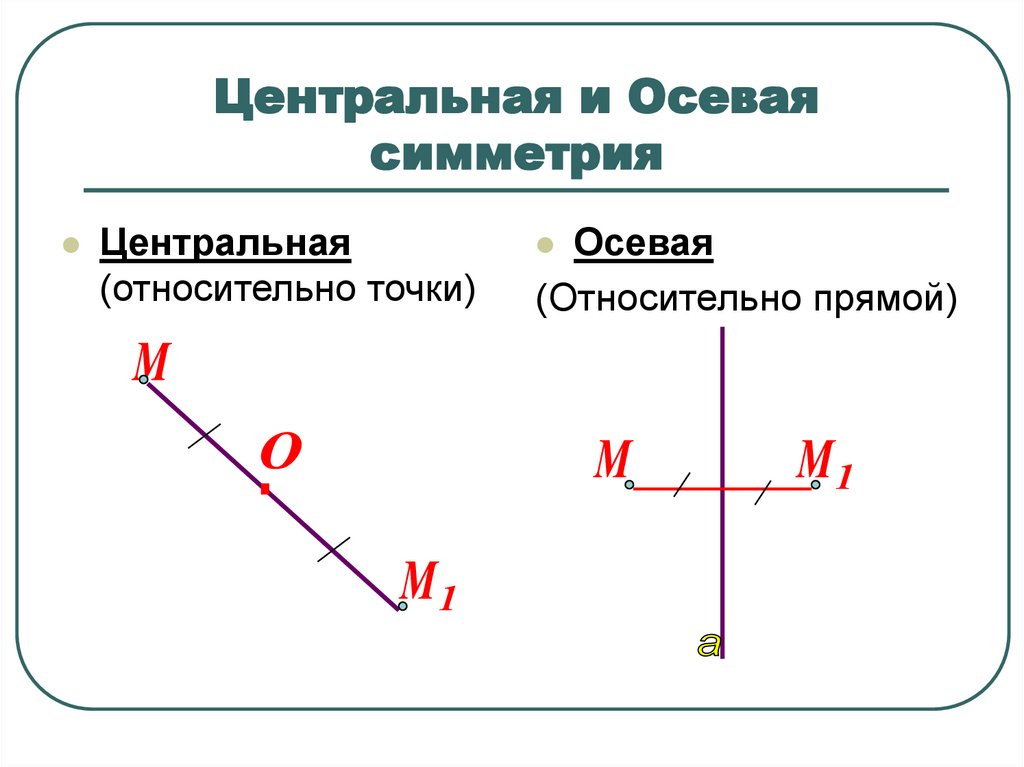
3. Центральная и Осевая симметрия

Центральная
(относительно точки)
Осевая
(Относительно прямой)

4.

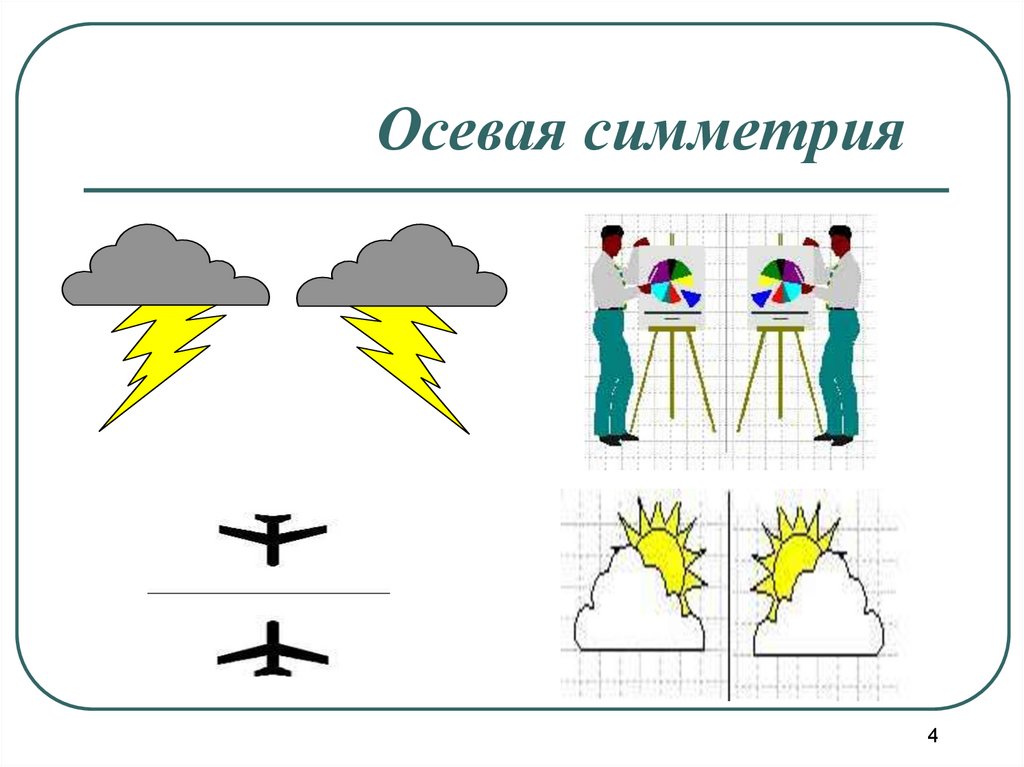
Осевая симметрия
4

5.

Центральная симметрия
C'
B
A
B'
C
5

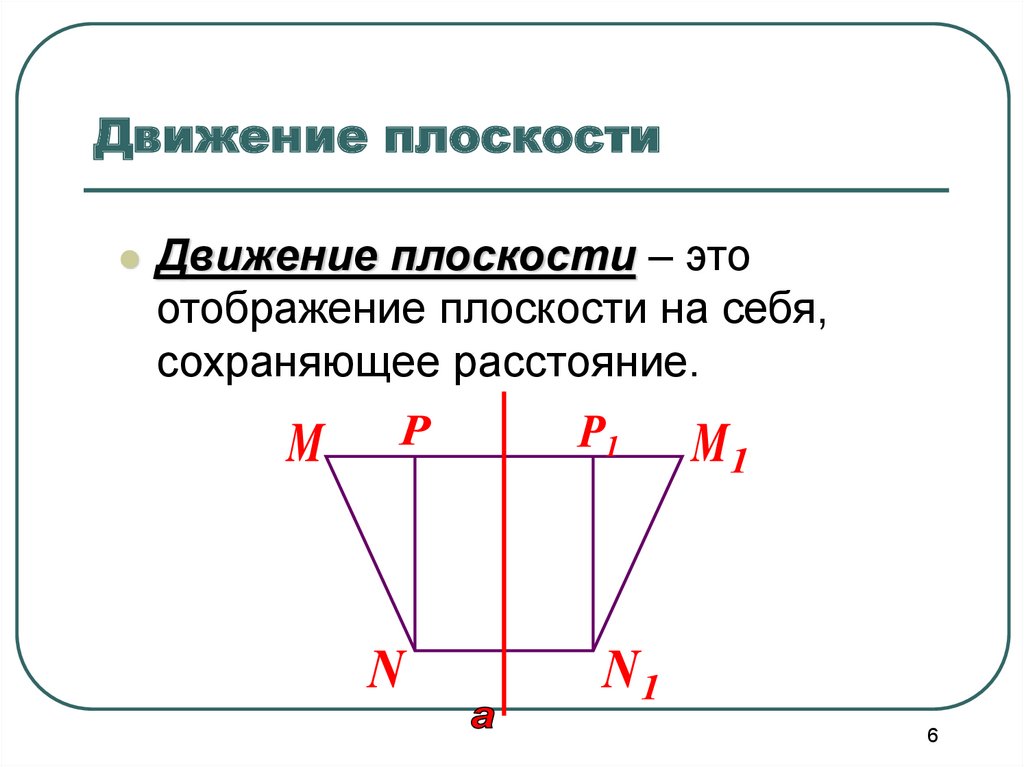
6. Движение плоскости

Движение плоскости – это
отображение плоскости на себя,
сохраняющее расстояние.
6

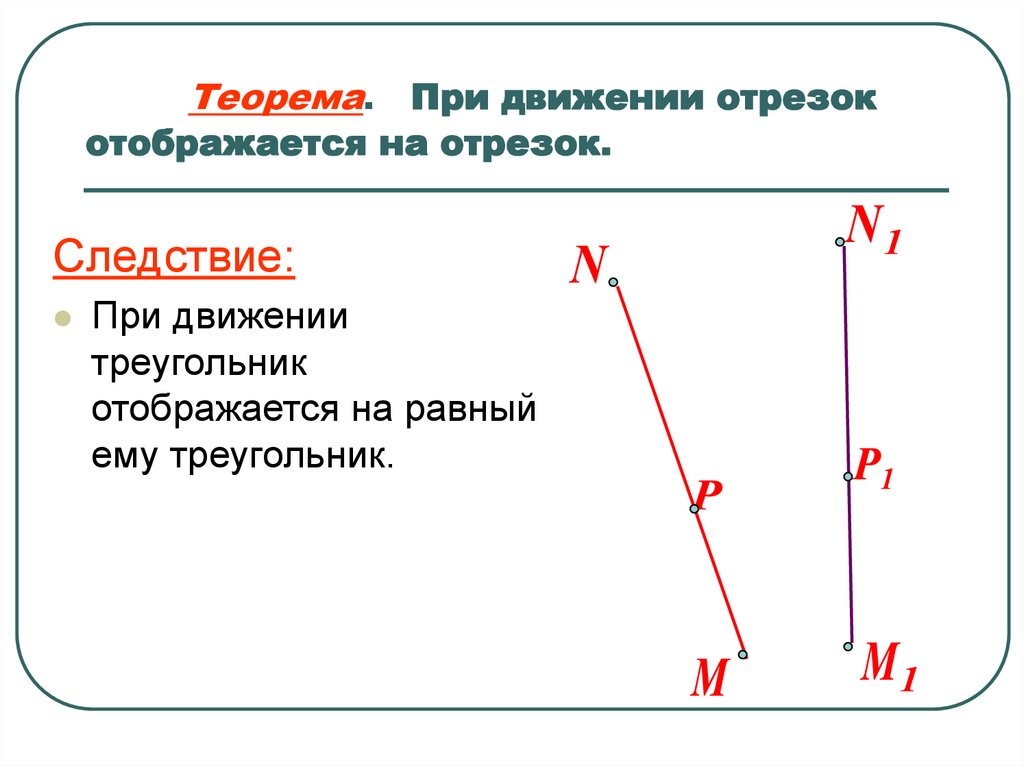
7. Теорема. При движении отрезок отображается на отрезок.

Следствие:
При движении
треугольник
отображается на равный
ему треугольник.

8. Наложение

Наложение- это отображение плоскости на себя.
8

9. Теорема. Любое движение является наложением.

Следствие:
При движении любая
фигура отображается на
равную ей фигуру.
Фигуры называются равными,
если существует движение,
отображающее одну из них на другую.

10. Задания

1.
2.
3.
Построить точки, симметричные А и В
относительно прямой l.
Построить треугольник, симметричный
данному относительно прямой а
Построить квадрат, симметричный
данному относительно точки М

11. Задания

4. Начертить симметричные фигуры
относительно прямой. Обозначить оси
симметрии.

12. Задания

5. Дан четырехугольник ABCD.
Построить фигуру, симметричную
данной:
а) относительно точки D
б) относительно диагонали АС

13. Домашнее задание:

Дан пятиугольник АBCDE. Построить
симметричные ему пятиугольник:
а) относительно точки В
б) относительно DE