Similar presentations:
Площадь произвольного выпуклого четырёхугольника. Триангуляция многоугольника. Теорема Бойяи-Гервина
1. Государственное бюджетное профессиональное образовательное учреждение «Нижегородский авиационный технический колледж» г.
Проект на тему:«ПЛОЩАДИ»
Выполнил: студент группы ТМ-17
Казаков А.В.
Проверил:
Кириллова М. П.
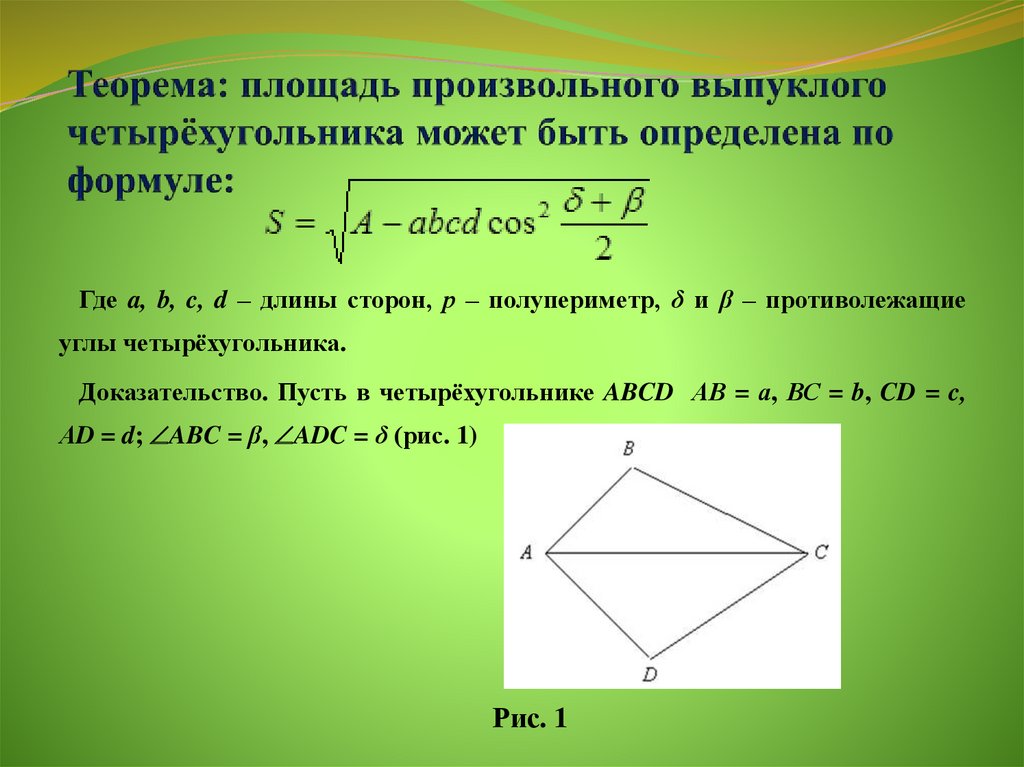
2. Теорема: площадь произвольного выпуклого четырёхугольника может быть определена по формуле:
Где a, b, c, d – длины сторон, р – полупериметр, δ и β – противолежащиеуглы четырёхугольника.
Доказательство. Пусть в четырёхугольнике ABCD АВ = а, ВС = b, CD = c,
АD = d; ABC = β, ADC = δ (рис. 1)
Рис. 1
3.
Из ABC в силу теоремы косинусов:AC 2 a 2 b2 2ab cos
Из ADC :
AC 2 c 2 d 2 2cd cos .
Приравнивая правые части этих выражений, получим:
a b 2ab cos c d 2cd cos ,
2
или
2
2
2
a 2 b2 c 2 d 2 2ab cos 2cd cos .
(1.2)
Найдём площадь четырёхугольника ABCD как сумму площадей треугольников ABC и ADC:
1
1
S ab sin cd sin ,
2
2
4.
откуда4S 2ab sin 2cd sin
(1.3)
В равенствах (1.2) и (1.3) обе части возведём в квадрат, а затем почленно сложим:
(a 2 b 2 c 2 d 2 ) 2 16S 2 (2ab cos 2cd cos ) 2
(2ab sin 2cd sin )
2
Выполним равносильные преобразования, получим
,
S A abcd cos
2
2
5.
Следствие 1. Площадь произвольногочетырёхугольника, вписанного в окружность,
вычисляется по формуле Брахмагупты:
Следствие 2. Площадь произвольного
четырёхугольника, описанного около окружности,
вычисляется по формуле:
Следствие 3. Площадь четырёхугольника,
вписанного в окружность и описанного около
окружности, может быть вычислена по формуле:
6.
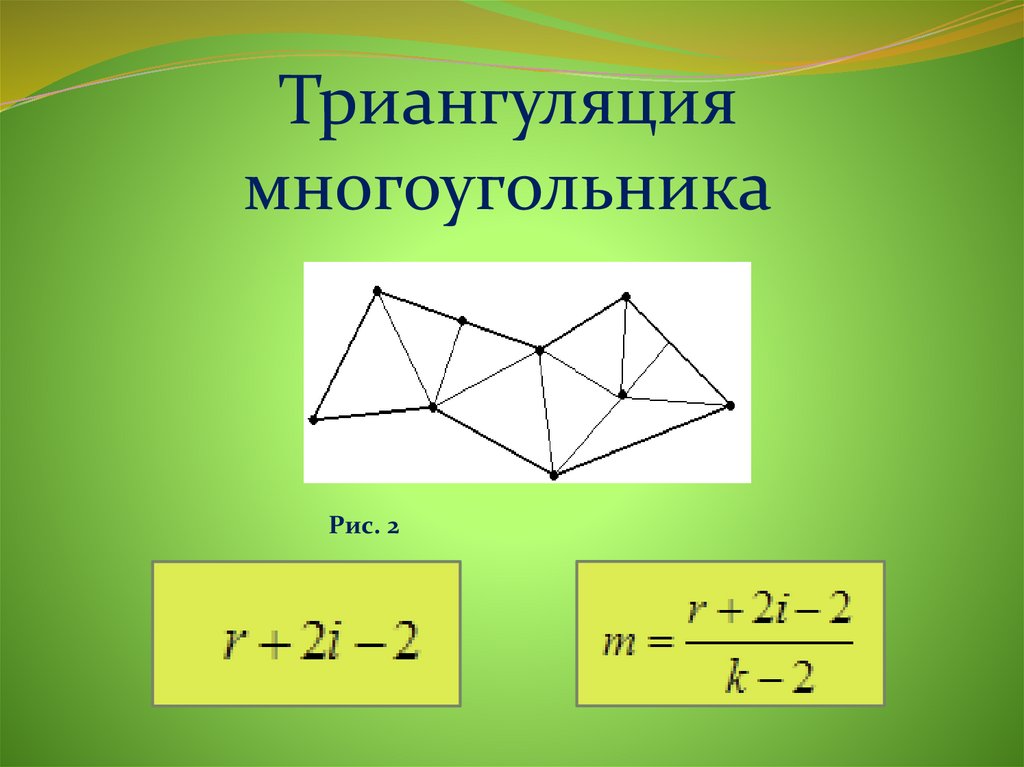
Триангуляциямногоугольника
Рис. 2
7.
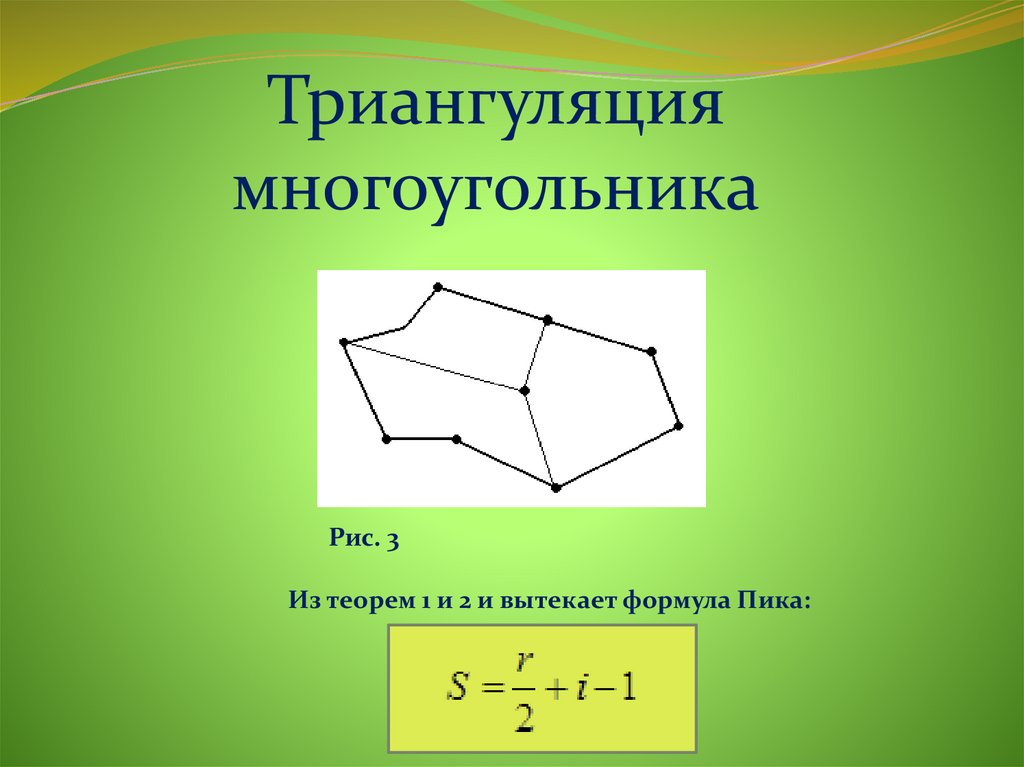
Триангуляциямногоугольника
Рис. 3
Из теорем 1 и 2 и вытекает формула Пика:
8.
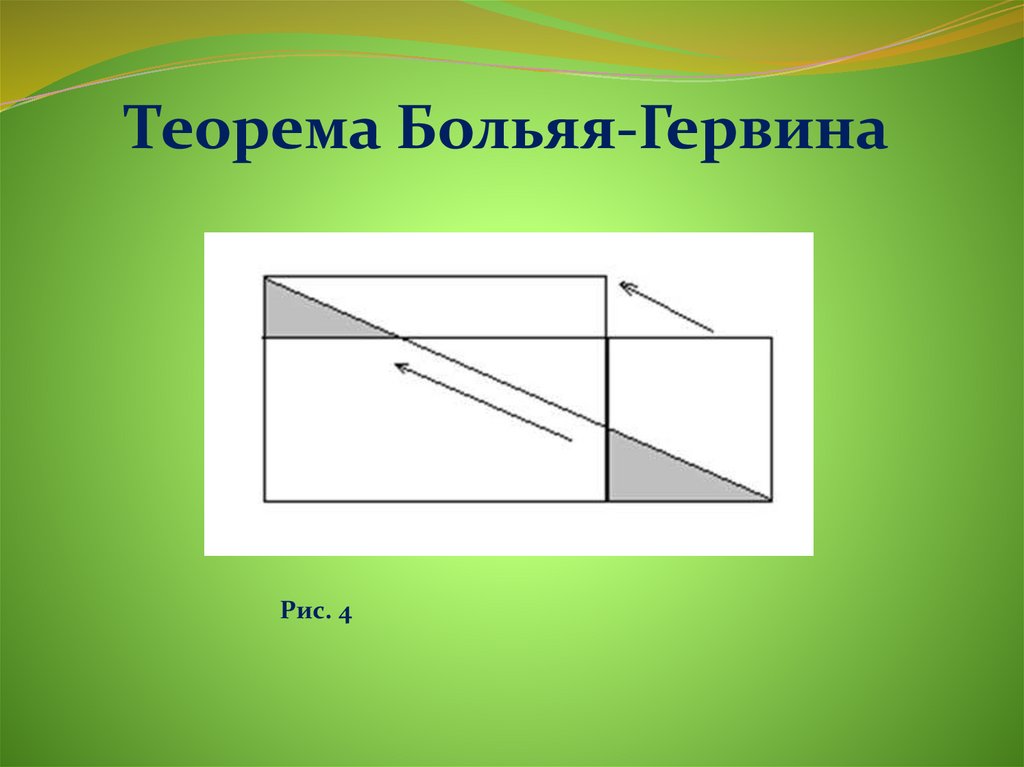
Теорема Больяя-ГервинаРис. 4
9.
Теорема Больяя-ГервинаРис. 5, а
Рис. 5, б
Рис. 6
10.
Задача 1.Дано: выпуклый четырёхугольник
Докажите, что этот четырёхугольник есть трапеция.
Доказательство.
Sчет
S1 S2
2
Рис. 7
S1 2 S1 S2 S2 . С другой стороны,
S S1 S 2 S3 S 4 (рис.7). S1 2 S1 S2 S2 S1 S2 S3 S4 ,
следовательно
2 S1 S2 S3 S4 , но S1 S 2 S3 S 4 , (рис. 7), следовательно
2 S3 S4 S3 S4 , следовательно S3 2 S3 S4 S4 0 , тогда
S3 S 4
означает, что
2
0 , следовательно S 3 S 4 и S3 S 2 S 4 S 2 , т. е.
BC || AD , т. е. четырёхугольник ABCD - трапеция.
S ABC S ACD , а это
11.
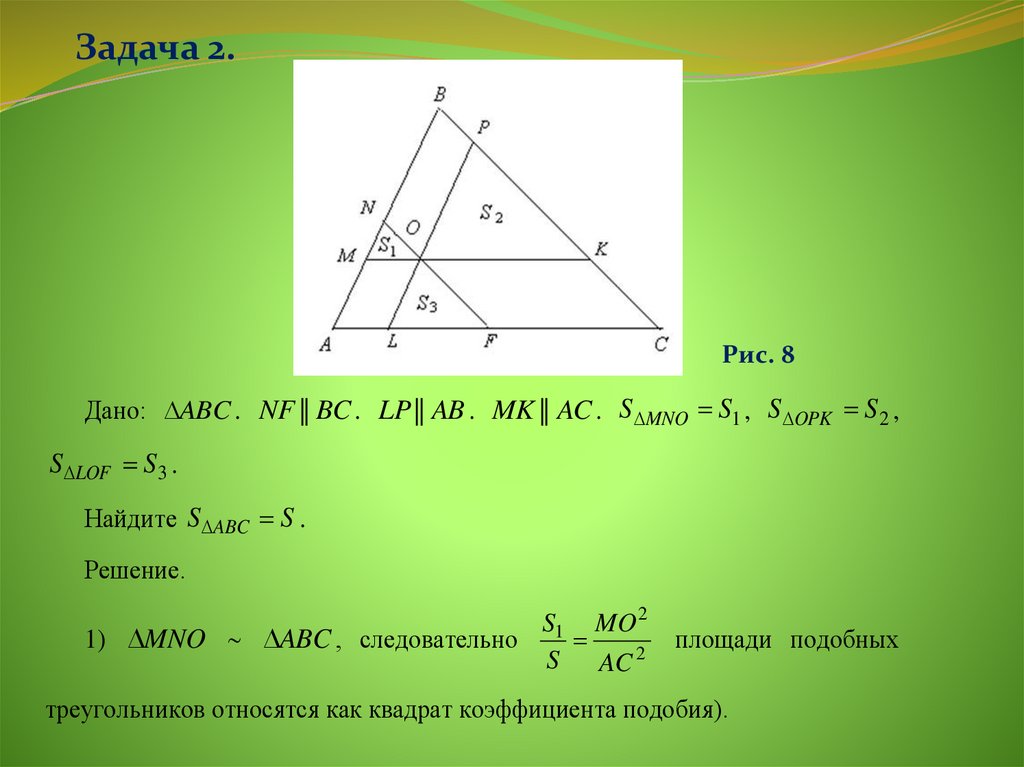
Задача 2.Рис. 8
Дано: ABC . NF || BC . LP || AB . MK || AC . S MNO S1 , S OPK S 2 ,
S LOF S3 .
Найдите S ABC S .
Решение.
S1 MO 2
1) MNO ABC , следовательно
S
AC 2
площади подобных
треугольников относятся как квадрат коэффициента подобия).
12.
Задача 2 (продолжение)2)
MO S 2 OK 2
;
;
2
S AC S AC
S1
S1 S 2 S3
S
S2
OK
;
S AC
S3
LF
.
S AC
MO OK LF AC
1.
AC
AC
2
S1 S2 S3 S , отсюда S S1 S2 S3 .








 mathematics
mathematics








