Понятие вектора

1.

2. ВЕКТОРЫ

3.

4.

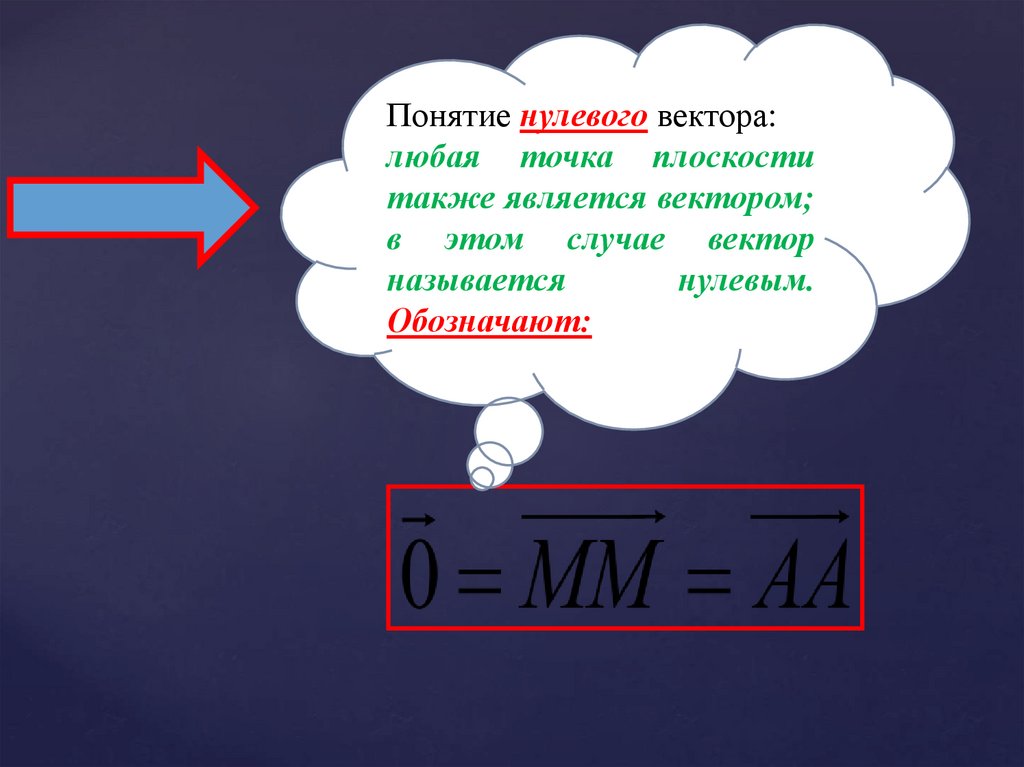
Понятие нулевого вектора:
любая точка плоскости
также является вектором;
в этом случае вектор
называется
нулевым.
Обозначают:

5.

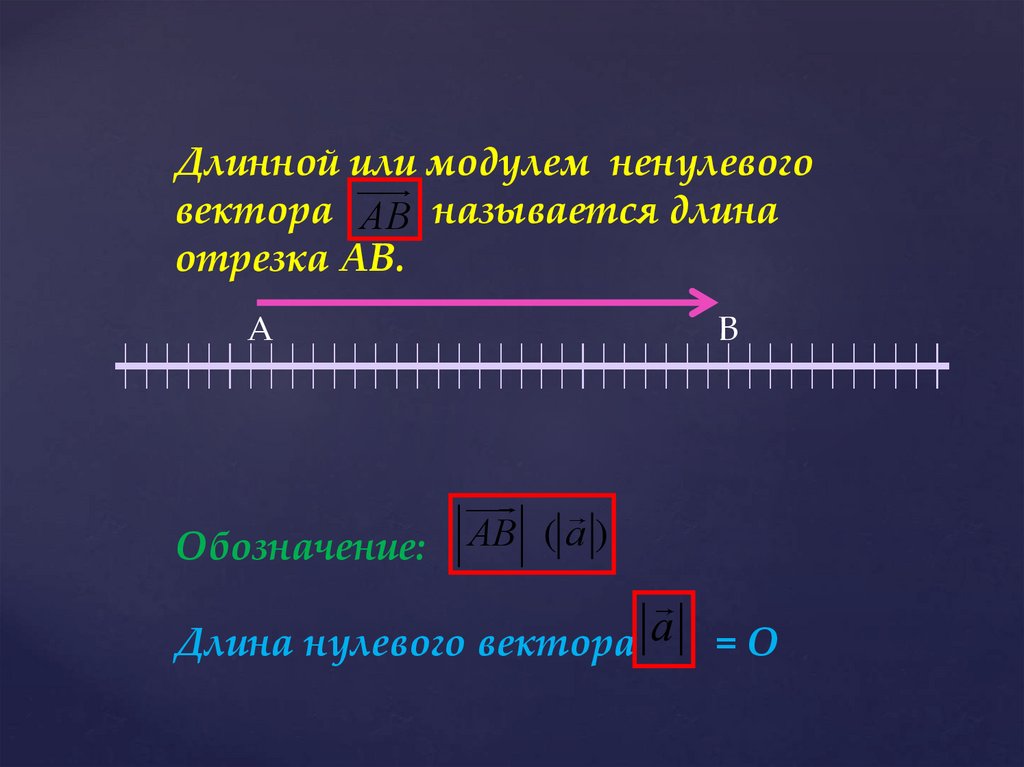
Длинной или модулем ненулевого
вектора АВ называется длина
отрезка АВ.
А
Обозначение:
В
АВ ( а )
Длина нулевого вектора а
=О

6.

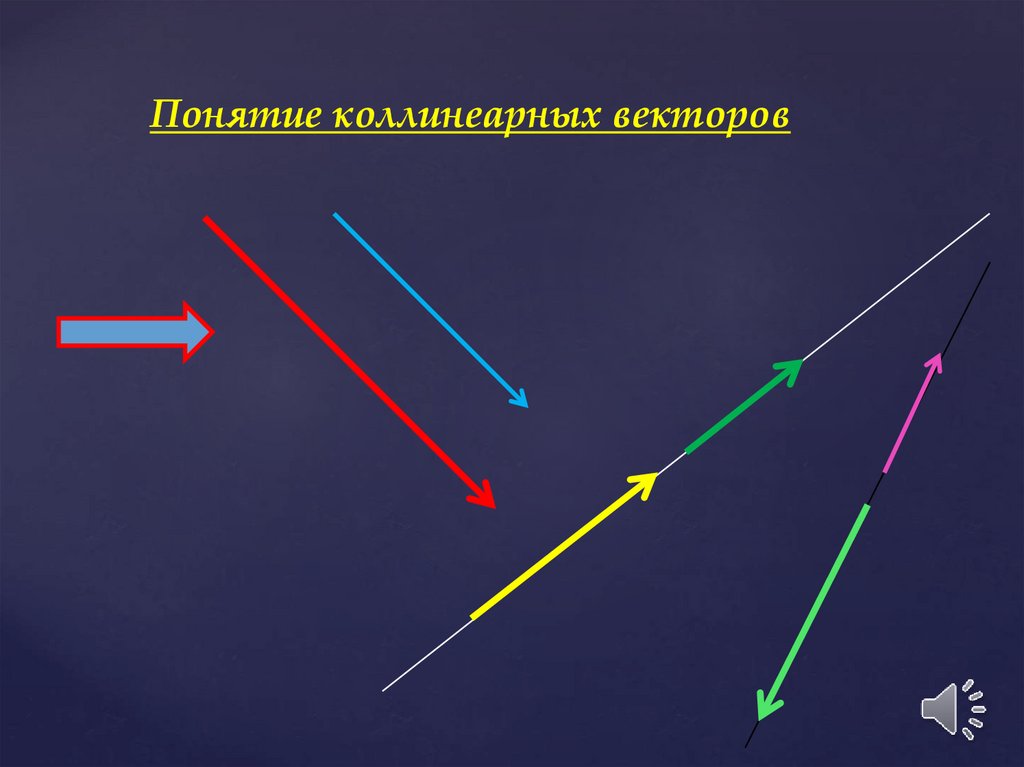
Понятие коллинеарных векторов

7. a c , b d , a k, e c

а
к
{
с
d
е
b
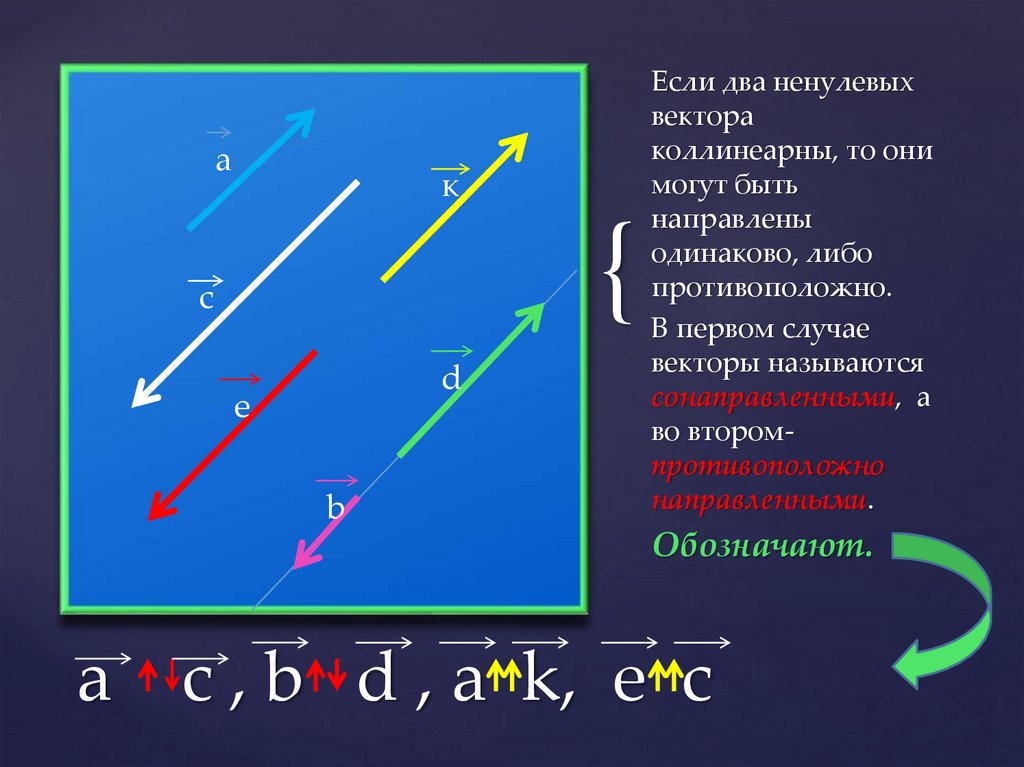
Если два ненулевых
вектора
коллинеарны, то они
могут быть
направлены
одинаково, либо
противоположно.
В первом случае
векторы называются
сонаправленными, а
во второмпротивоположно
направленными.
Обозначают.
a
c , b d , a k, e c

8. Если АВ СД и |АВ|=|СД|, то АВ = СД

Векторы
называются
равными,
если они
сонаправлены и их
длины равны.
Если АВ
В
Д
А
С
СД и |АВ|=|СД|, то АВ = СД

9.

А
В
М
К
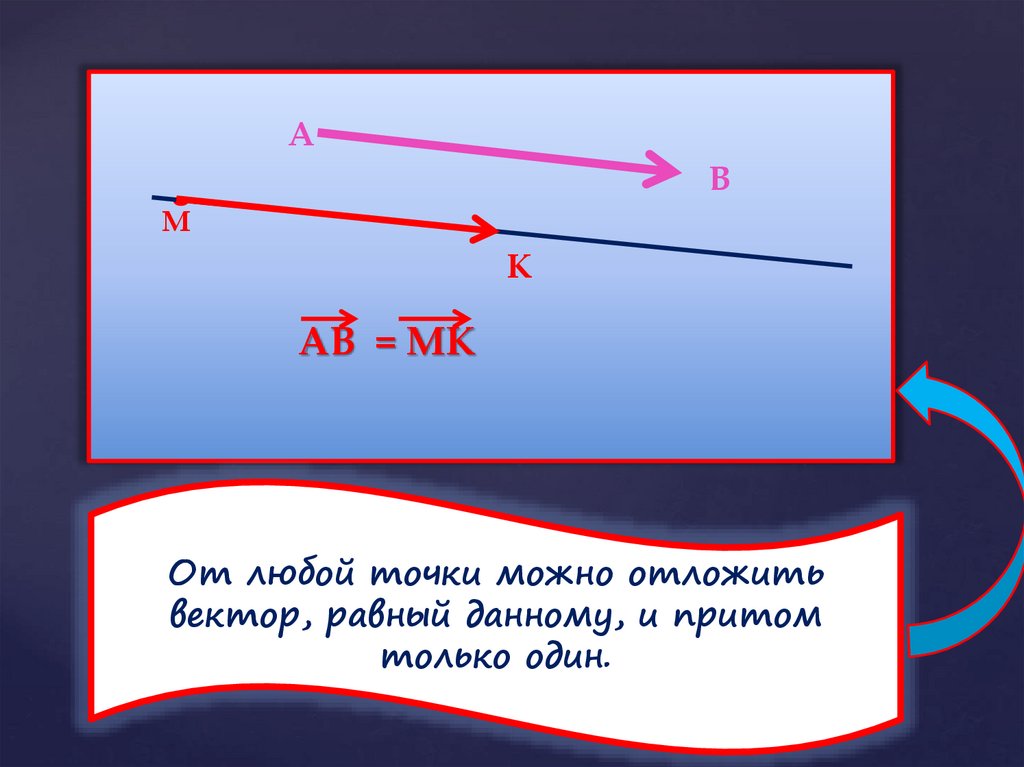
АВ = МК
От любой точки можно отложить
вектор, равный данному, и притом
только один.

10. Докажите ,что если векторы АВ и СД равны , то середины отрезков АД и ВС совпадают.

{
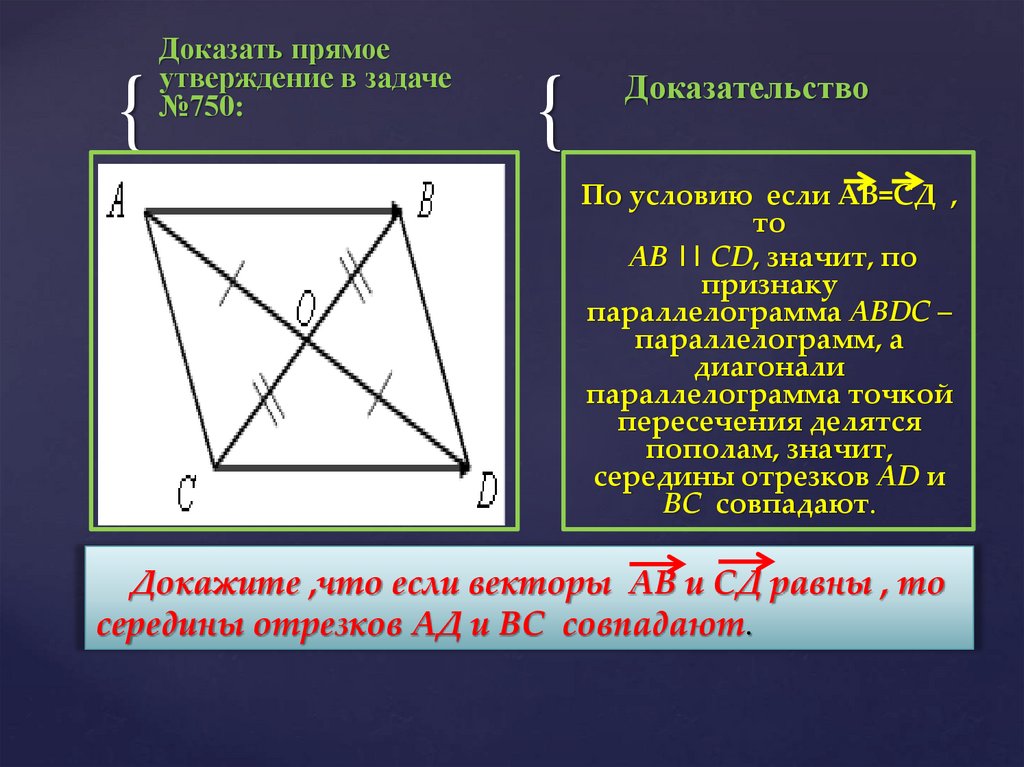
Доказать прямое
утверждение в задаче
№750:
{
Доказательство
По условию если АВ=СД ,
то
AB || CD, значит, по
признаку
параллелограмма АВDС –
параллелограмм, а
диагонали
параллелограмма точкой
пересечения делятся
пополам, значит,
середины отрезков AD и
BC совпадают.
Докажите ,что если векторы АВ и СД равны , то
середины отрезков АД и ВС совпадают.

11. Домашнее задание

Изучить материал пунктов 76–78;
ответить на вопросы 1–6, с. 213
учебника; решить задачи №№ 740
(б), 747.
Домашнее задание

12. Сумма векторов. Правило треугольника .

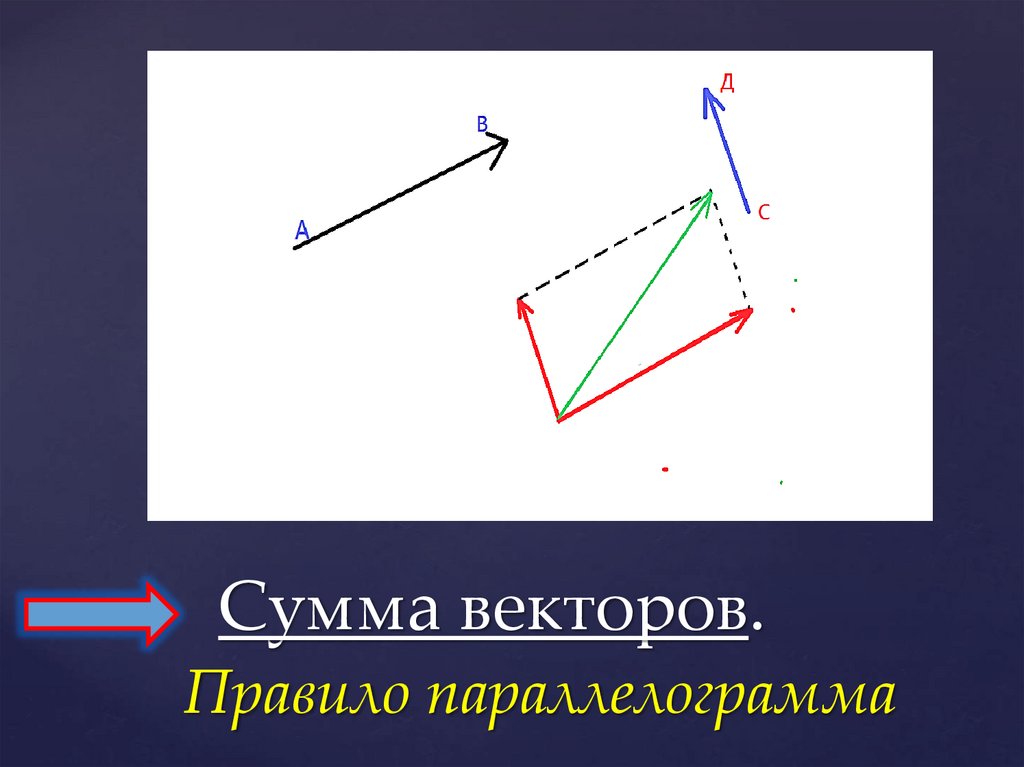
13. Сумма векторов. Правило параллелограмма

14.

Презентация к уроку
геометрии.
9 класс.
Тема
«Сложение векторов».
Подготовила
Бурлакова М.А.
учитель математики МКОУ
«Касторенская средняя
общеобразовательная школа №1»

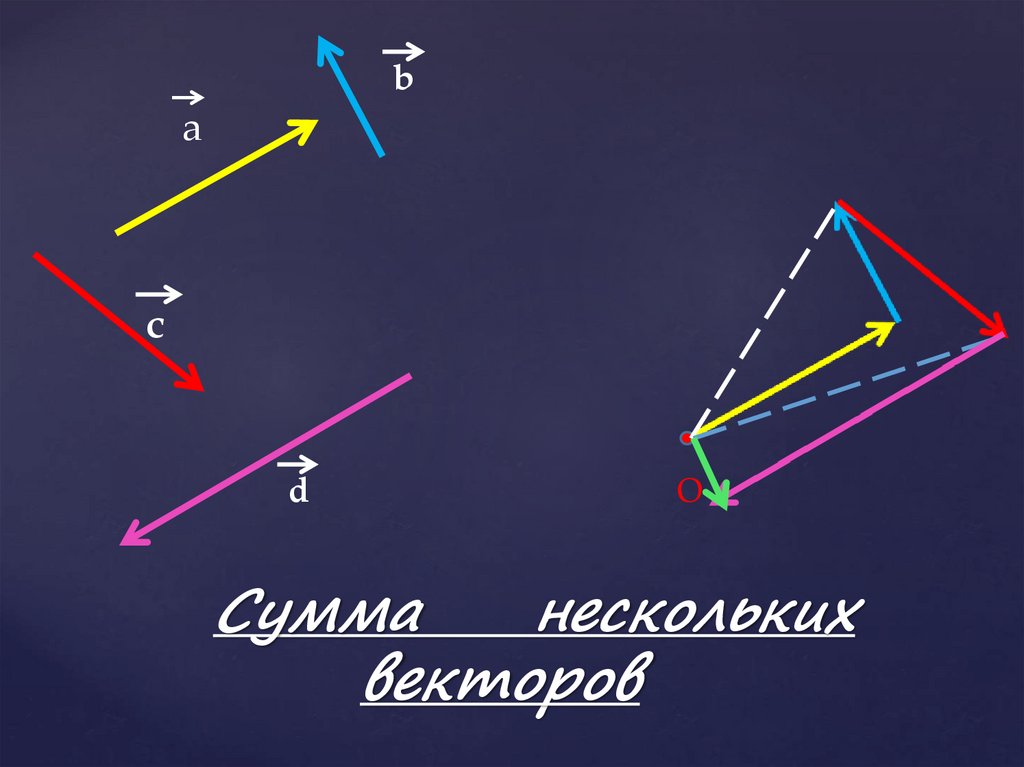
15. Сумма нескольких векторов

b
a
с
d
O
Сумма
нескольких
векторов

16. Частное использование этого правила в физике, например при сложении двух сил.

17. При сложении нескольких векторов сумма данных векторов может быть равна нулевому вектору, если начало первого вектора совпадает

с концом
последнего вектора
.

18. Практическое задание

Начертите попарно неколлинеарные
векторы a, b и c . Постройте
векторы
a b , b a, a c , (a b ) c , a (b c ), (a c ) b
Вопрос учащимся.
– Какие из построенных векторов равны
друг другу?
Практическое задание

19.

ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ
Для
а, bbиис ссправедливы
справедливы
равенства:
Длялюбых
любыхвекторов
векторов а,
равенства:
Переместительный закон
a + b=b+a
Сочетательный закон
( a + b) + c = a + ( b + c )

20. Самостоятельная работа

{
Вариант I
{
Вариант II
1. Начертите пять попарно
неколлинеарных векторов
a, b , c , d ,. e
Постройте вектор
.
2. Упростите выражение:
PQ EF AE QA
Самостоятельная работа

21. Решить задачу № 762 ( б).

Решение
Найдем сумму векторов АВ и АС по правилу
параллелограмма
AB AC AD
Найдем длину вектора АД.
По условию AB = AC = a, то ABDC – ромб;
диагонали ромба взаимно перпендикулярны: AD
BC и точкой пересечения делятся пополам,
тогда BO = OC = и AO = OD. Из
прямоугольного треугольника AOC по теореме
Пифагора найдем AO :
2
a2
3a 2 a 3
a
2
AO =
;
AC OC a a
4
4
2
2
AD = 2AO = 2 a 3 = a. 3 Значит, AD = a.
2
Ответ: a.
2
2
2
Решить задачу № 762 ( б).

22. Домашнее задание

Изучить материал пунктов 79–81;
решить задачи №№ 754, 759.
Домашнее задание

23. Вычисление корня n-ой степени

ВЫЧИСЛЕНИЕ
КОРНЯ
N-ОЙ СТЕПЕНИ
Т

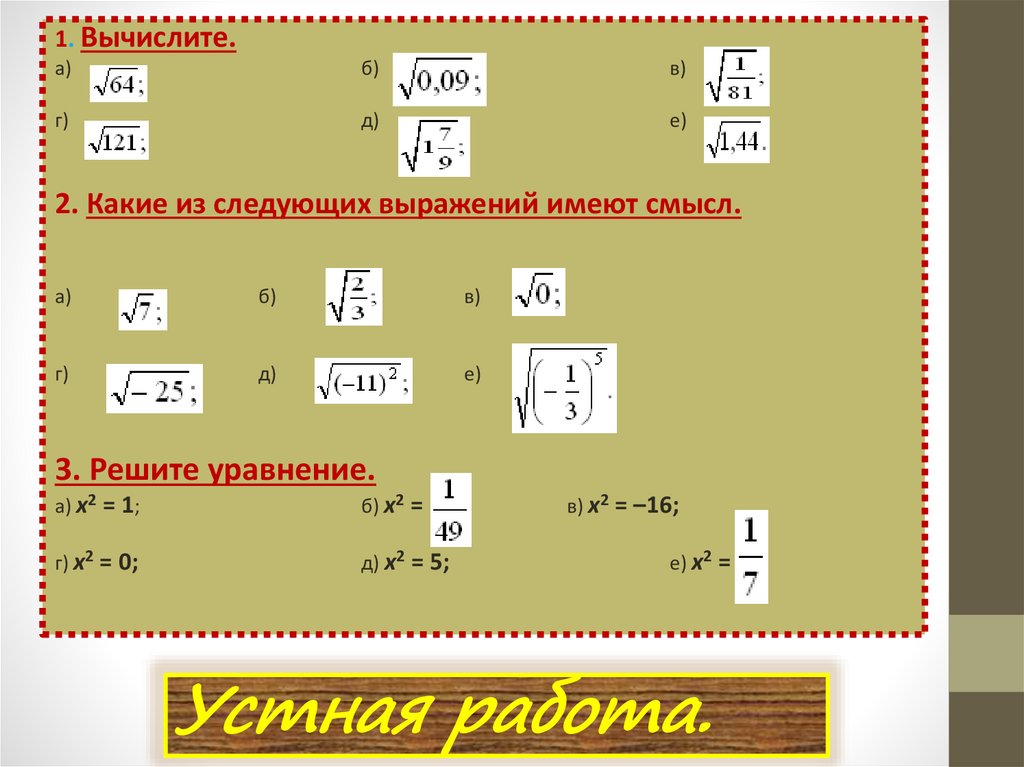
24. Устная работа.

1. Вычислите.
а)
б)
в)
г)
д)
е)
2. Какие из следующих выражений имеют смысл.
а)
б)
в)
г)
д)
е)
3. Решите уравнение.
а) х2 = 1;
б) х2 =
г) х2 = 0;
д) х2 = 5;
;
в) х2 = –16;
е) х2 = .
Устная работа.

25.

26. Работа в группах

1 группа
• 1. № 33.1, 33.2.
• 2. Прочитайте выражения.
а)
б)
в)
2 группа
• 1. Вычислите.
а)
б)
г)
г)
д)
в)
е)
д)
• 3. Какие из следующих
выражений имеют смысл.
• а)
б)
в)
г)
• 4. № 33.3.
д)
е)
2.
Найдите
выражения.
а)
б)
в)
г)
• 3. № 33.4 (а, б).
значение

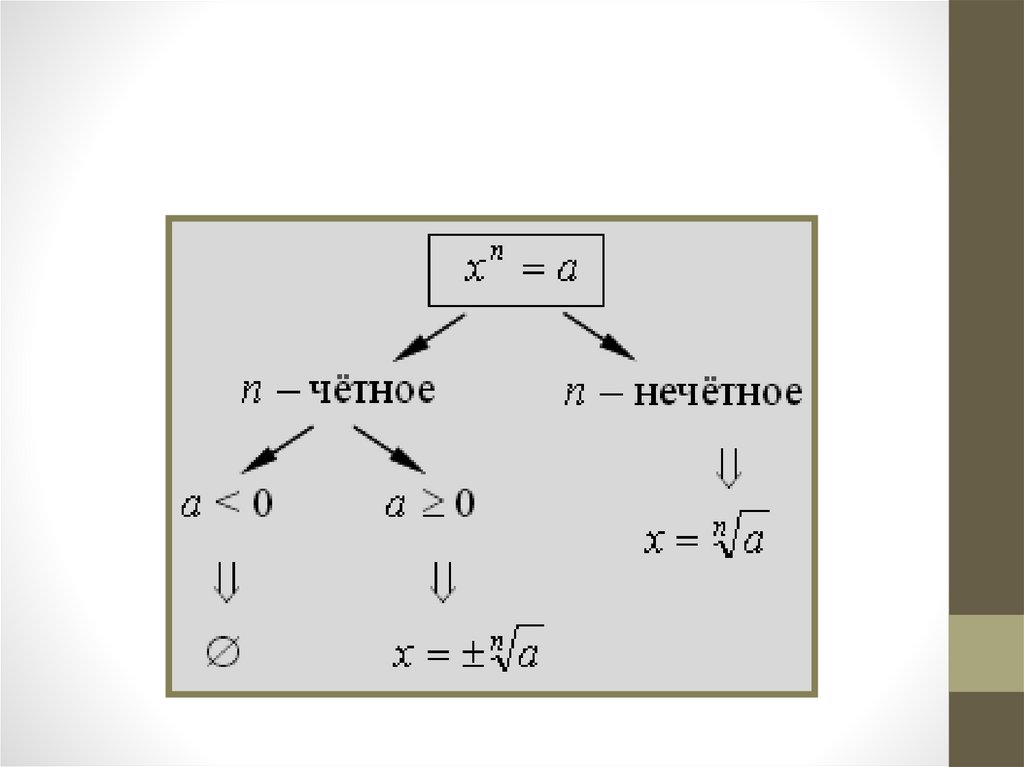
27. Вопросы учащимся: – Как графически можно решить уравнение вида хn = a? – Найдите корень уравнения х7 = 3. – Дайте определение

корня п-ой степени из
действительного числа.
– Сколько корней может иметь уравнение вида хn = a?
Отчего это зависит?
– Как вычислить корень п-ой степени из числа?
– Когда корень п-ой степени не имеет смысла?
Итоги урока.

28.

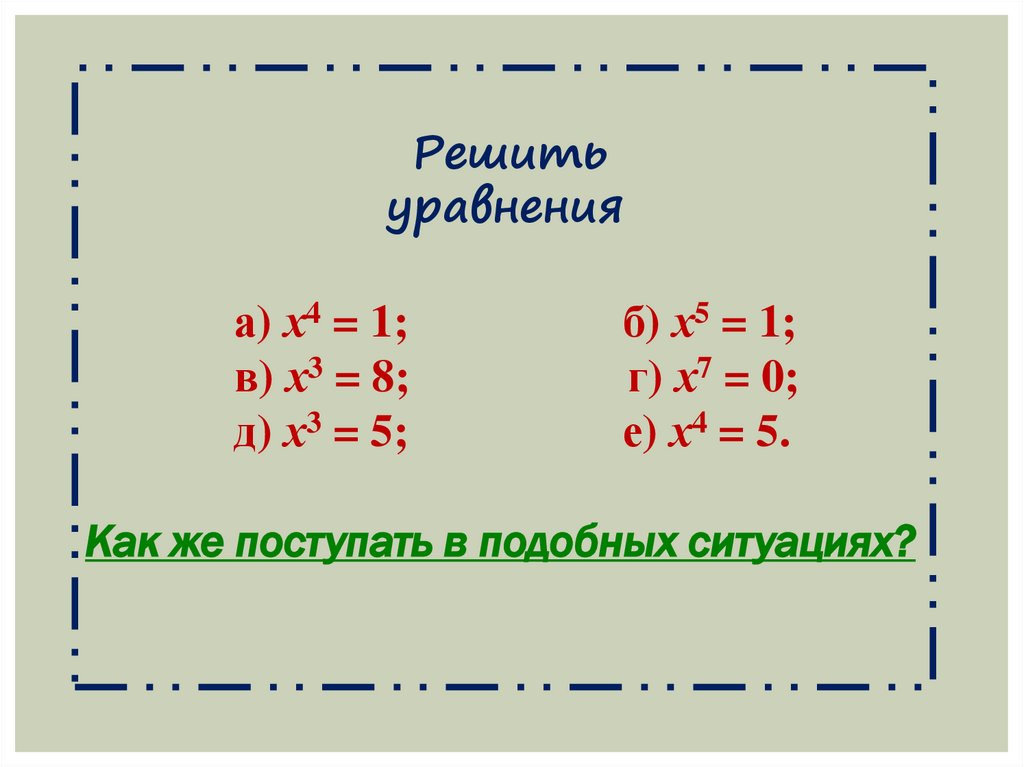
Решить
уравнения
а) х4 = 1;
в) х3 = 8;
д) х3 = 5;
б) х5 = 1;
г) х7 = 0;
е) х4 = 5.
Как же поступать в подобных ситуациях?