Similar presentations:
Поворот
1.
Презентация к уроку в 9классе
по теме:
«Поворот.»
Учитель математики:
Быкова Галина Петровна
2.
«Без движения —жизнь только
летаргический
сон».
Жан Жак Руссо
3.
4.
5.
6.
1. Не обладает центром симметриифигура, изображенная
на рисунке под буквой:
А
Б
В
Г
решение
7.
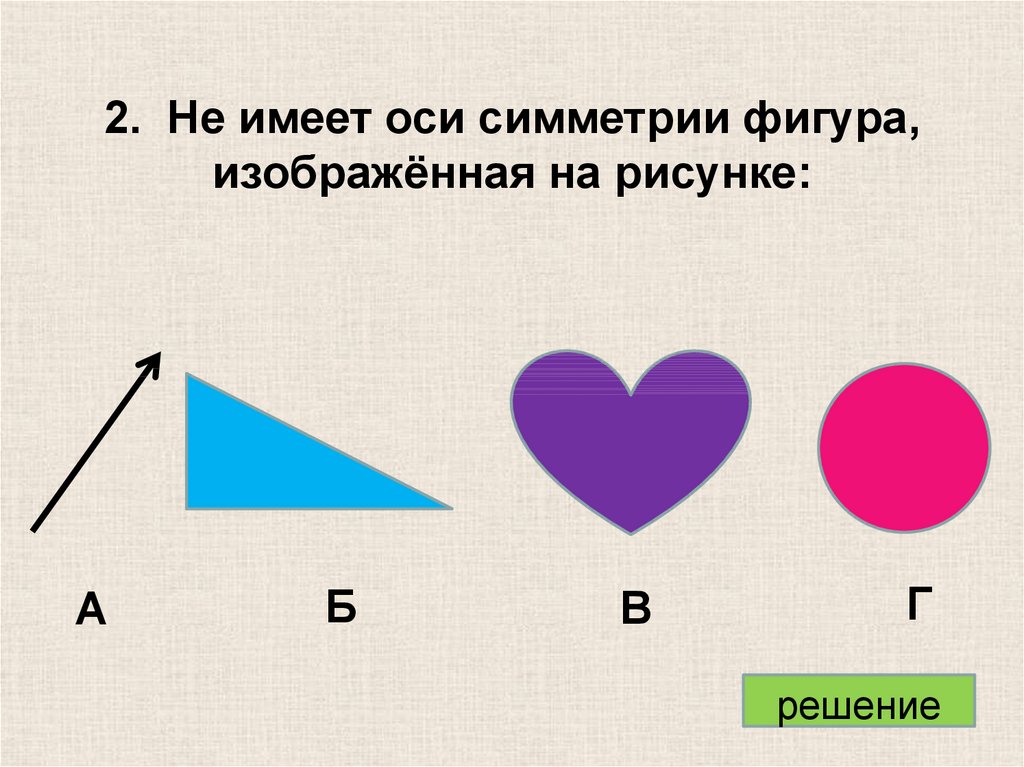
2. Не имеет оси симметрии фигура,изображённая на рисунке:
А
Б
В
Г
решение
8.
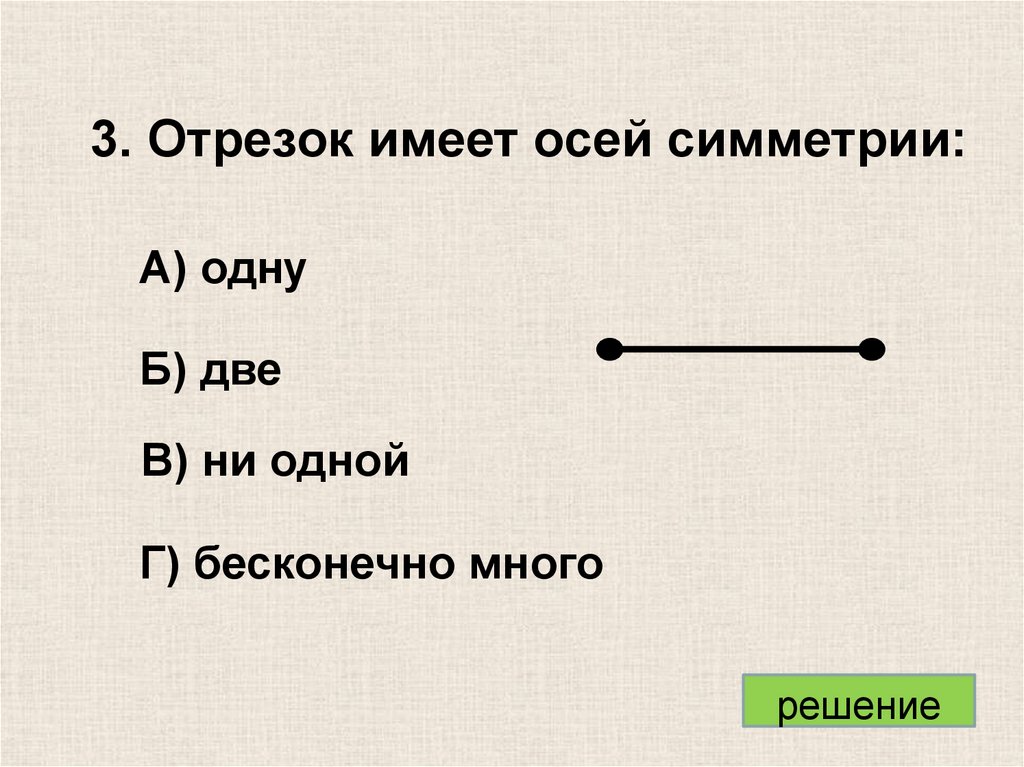
3. Отрезок имеет осей симметрии:А) одну
Б) две
В) ни одной
Г) бесконечно много
решение
9.
4. Центр симметрии имеет:А) параллелограмм;
Б) равносторонний треугольник;
В) трапеция;
Г) правильный пятиугольник.
решение
10.
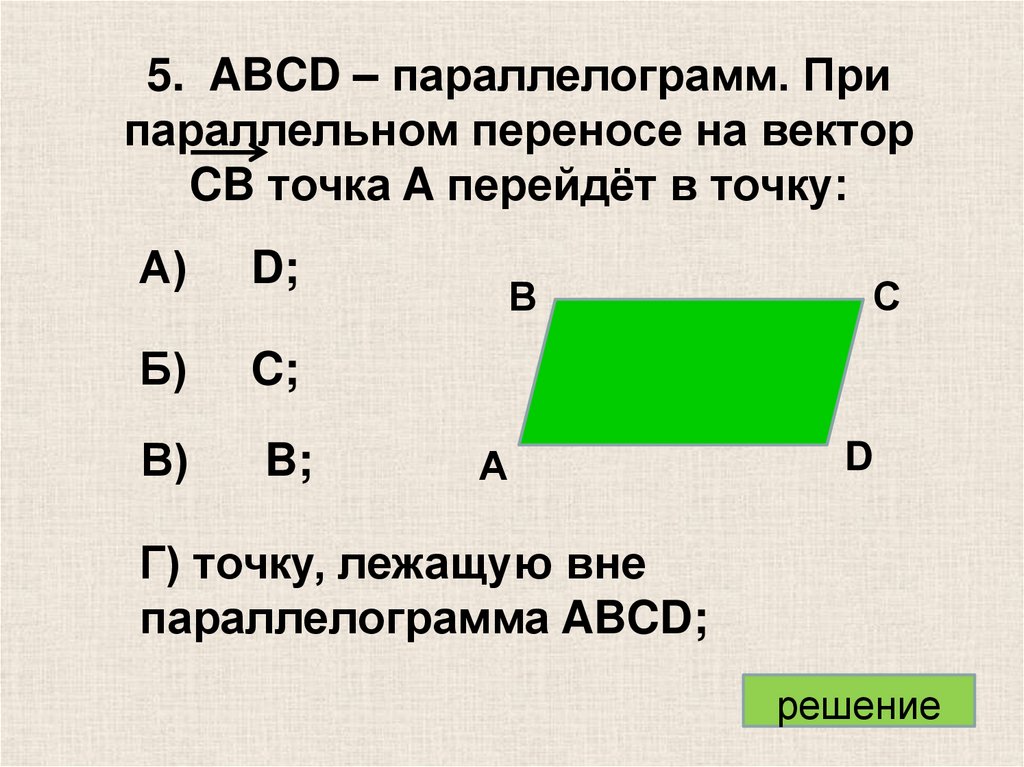
5. ABCD – параллелограмм. Припараллельном переносе на вектор
CB точка A перейдёт в точку:
А)
D;
Б)
C;
В)
B;
В
А
С
D
Г) точку, лежащую вне
параллелограмма ABCD;
решение
11.
6. При осевой симметрии прямая,проходящая через ось симметрии
будет отображаться на:
А) параллельную ей прямую;
Б) перпендикулярную ей прямую;
В) себя;
Г)
отрезок.
решение
12.
7. Точка A имеет координаты: x= - 5; y= 4. Тогдаточка C, симметричная точке A относительно
оси x, будет иметь координаты:
А) x= -5; y=- 4;
Б) x= 5; y=- 4;
В) x= 5; y= 4;
Г)
x= 4; y= -5;
решение
13.
8. При движении ромботображается на:
А) параллелограмм;
Б) квадрат;
В) произвольный четырёхугольник;
Г) ромб.
решение
14.
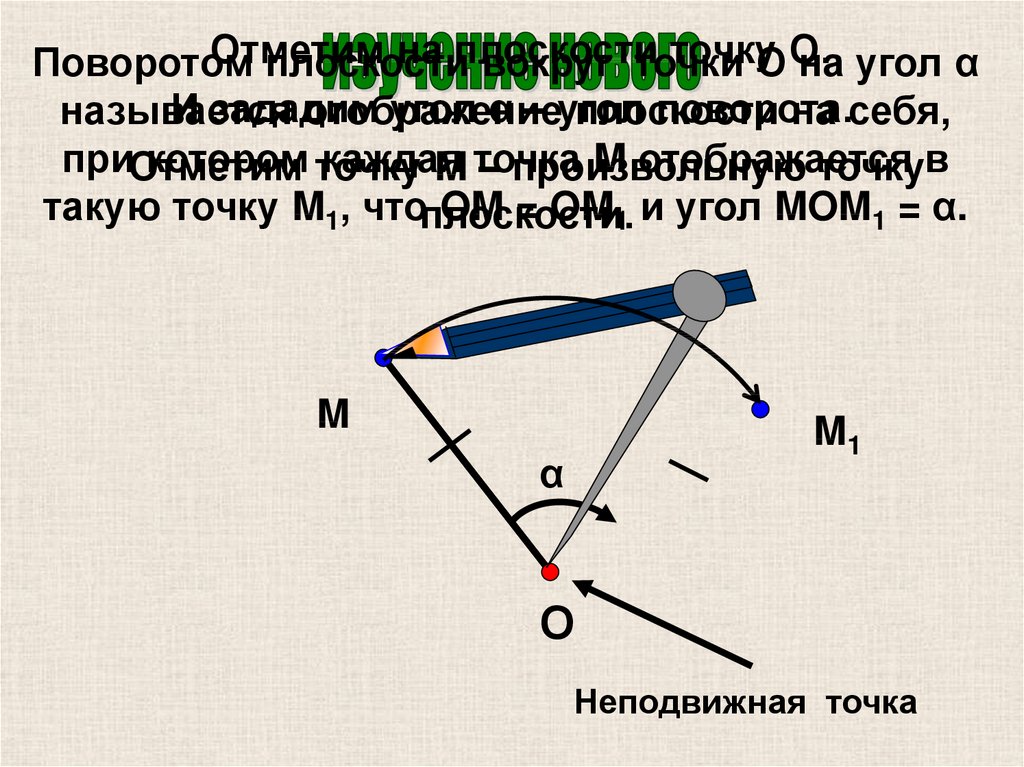
Отметимна плоскости
точку
Поворотом
плоскости
вокруг точки
О О.
на угол α
И зададим
угол α – угол
поворота.
называется
отображение
плоскости
на себя,
приОтметим
котором точку
каждая
M отображается
M точка
– произвольную
точкув
такую точку M1, чтоплоскости.
OM = OM1 и угол MOM1 = α.
M
M1
α
О
Неподвижная точка
15.
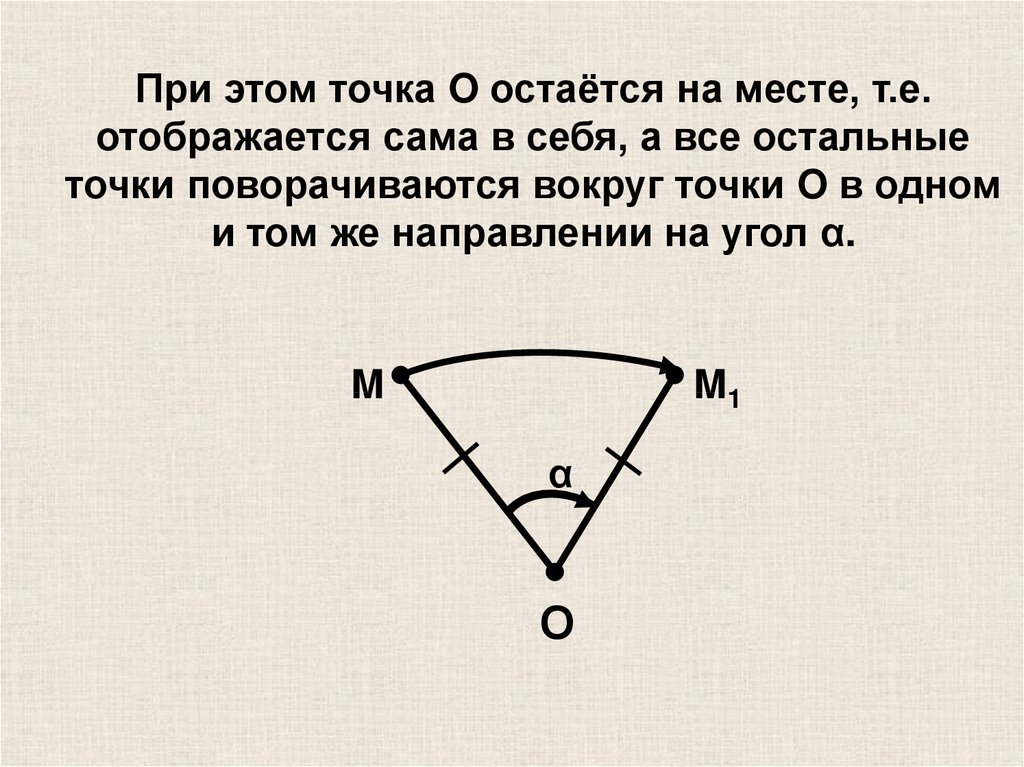
При этом точка O остаётся на месте, т.е.отображается сама в себя, а все остальные
точки поворачиваются вокруг точки O в одном
и том же направлении на угол α.
M
M1
α
О
16.
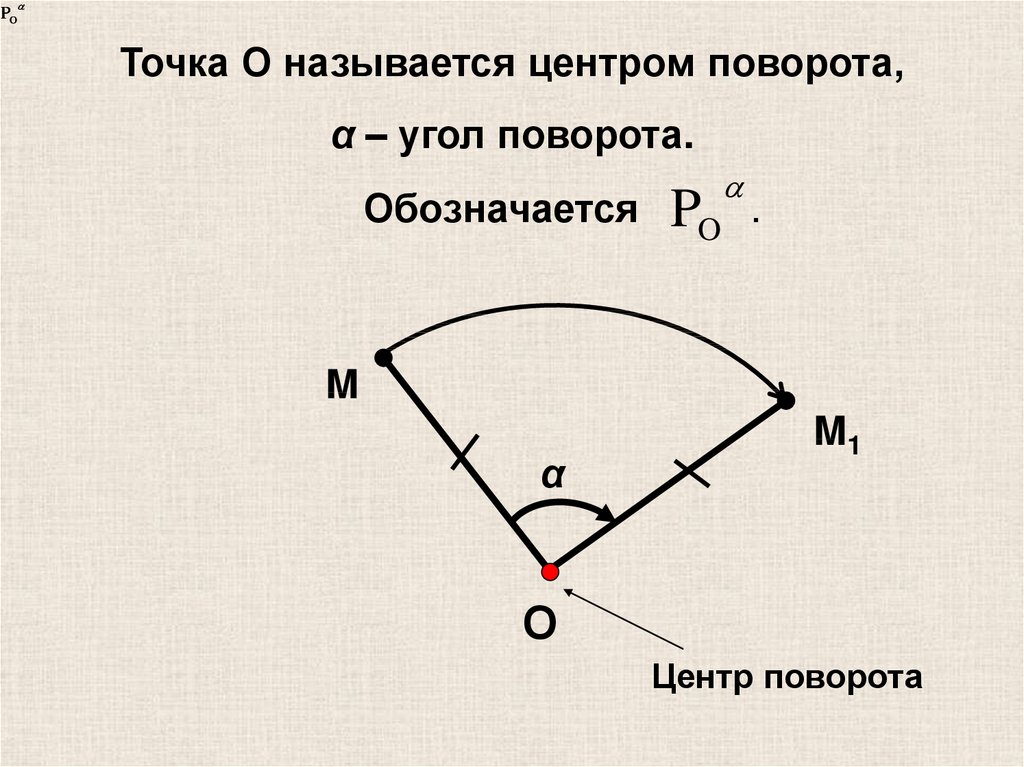
POТочка О называется центром поворота,
α – угол поворота.
Обозначается
PO
.
M
α
M1
О
Центр поворота
17.
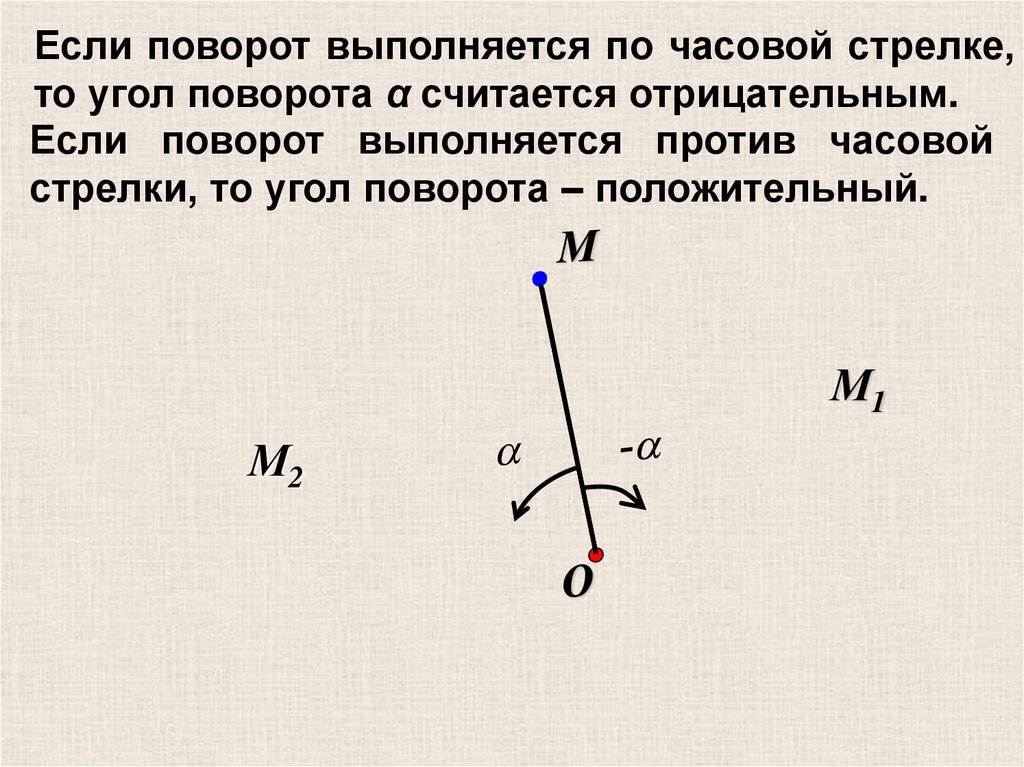
Если поворот выполняется по часовой стрелке,то угол поворота α считается отрицательным.
Если поворот выполняется против часовой
стрелки, то угол поворота – положительный.
М1
М2
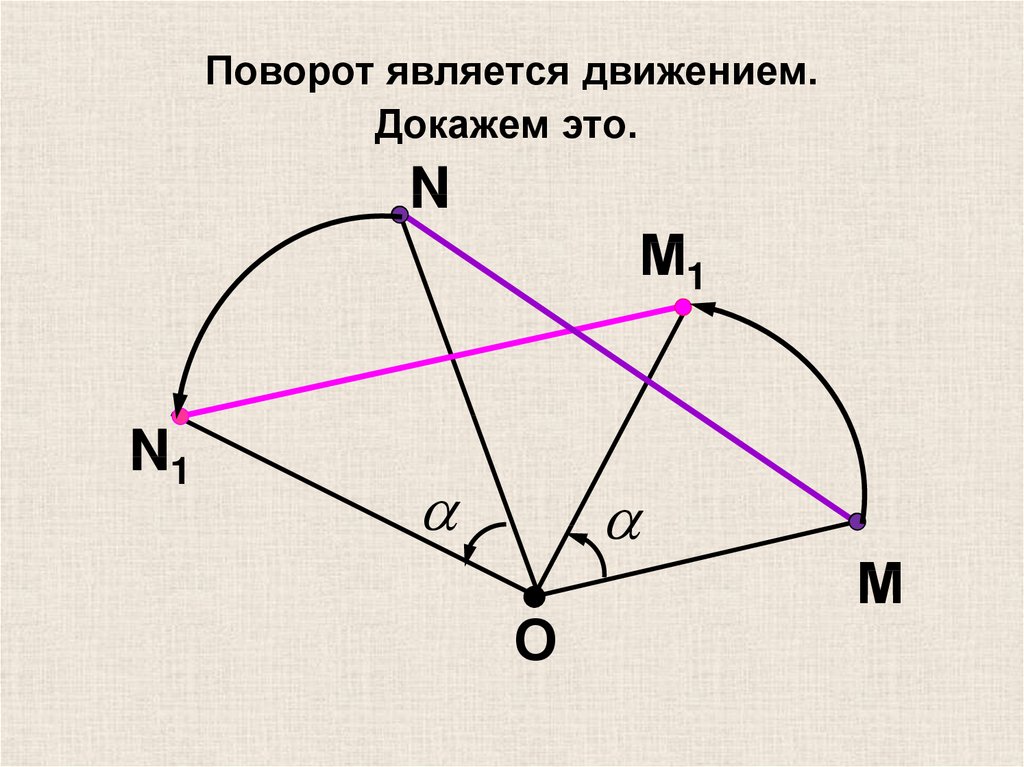
18. Поворот является движением. Докажем это.
NМ1
N1
О
М
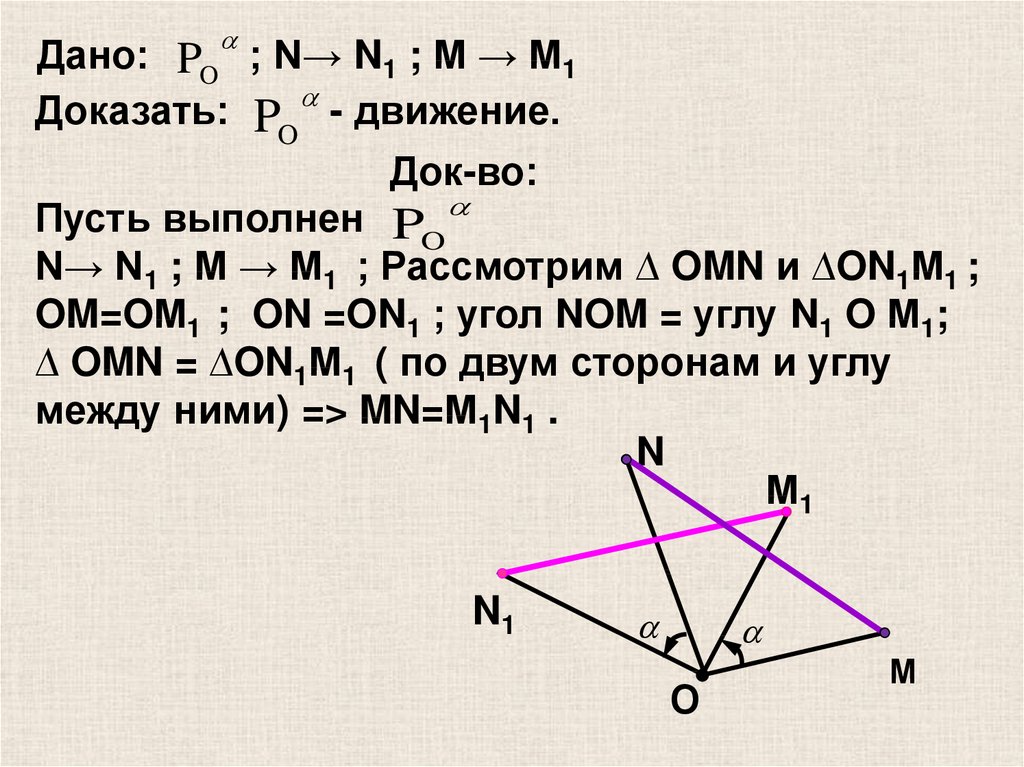
19. Дано: ; N→ N1 ; M → М1
Дано: PO ; N→ N1 ; M → М1Доказать: PO - движение.
Док-во:
Пусть выполнен PO
N→ N1 ; M → М1 ; Рассмотрим ∆ OMN и ∆ON1М1 ;
OM=OМ1 ; ON =ON1 ; угол NOM = углу N1 O М1;
∆ OMN = ∆ON1М1 ( по двум сторонам и углу
между ними) => MN=М1N1 .
N
М1
N1
О
М
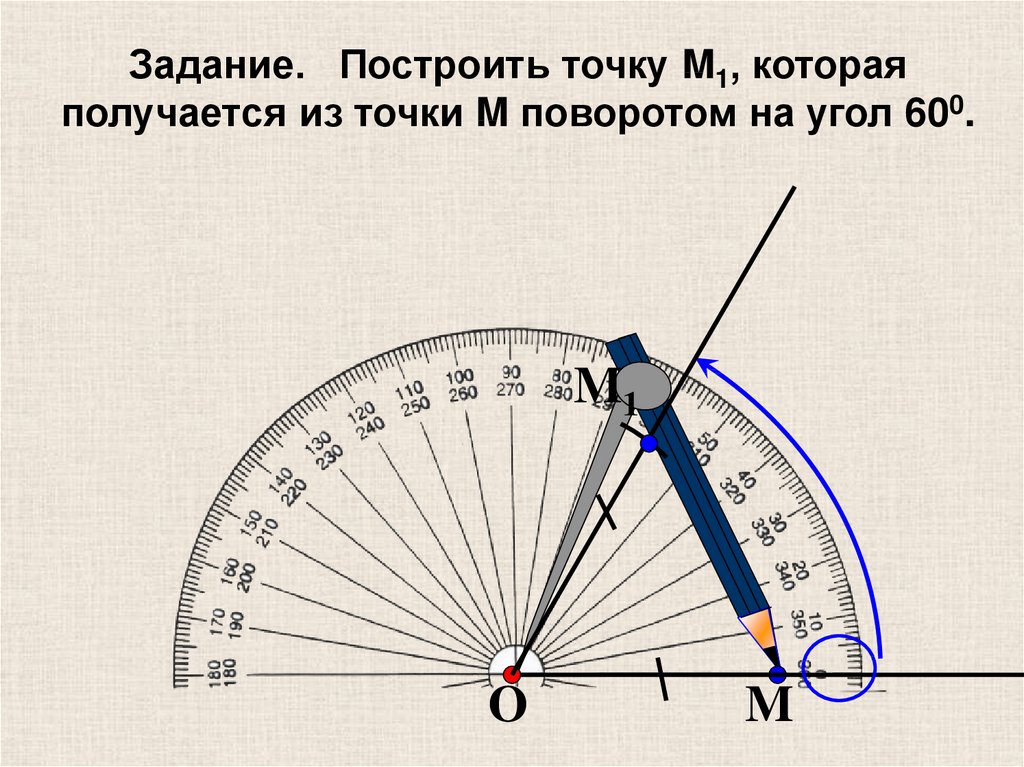
20.
Задание. Построить точку M1, котораяполучается из точки M поворотом на угол 600.
M1
O
M
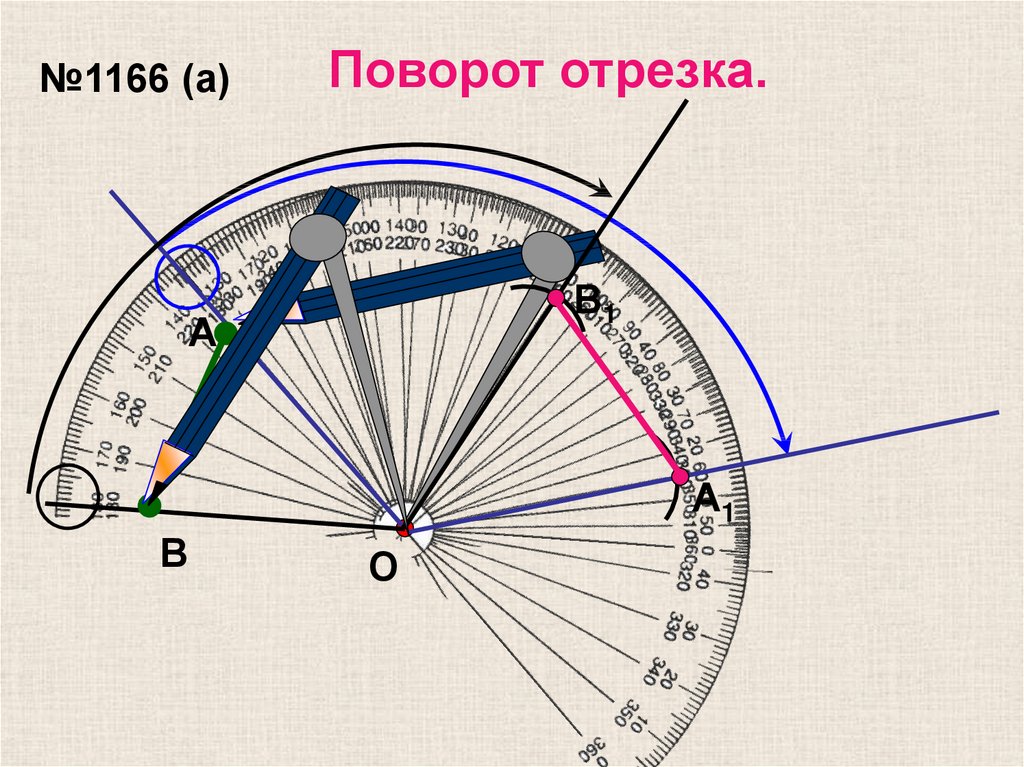
21.
№1166 (а)Поворот отрезка.
В1
А
А1
В
О
22.
Задание. Построить фигуру, котораяполучится при повороте отрезка AB на угол
-1000 вокруг точки А.
B1
B
A
центр поворота –
неподвижная точка
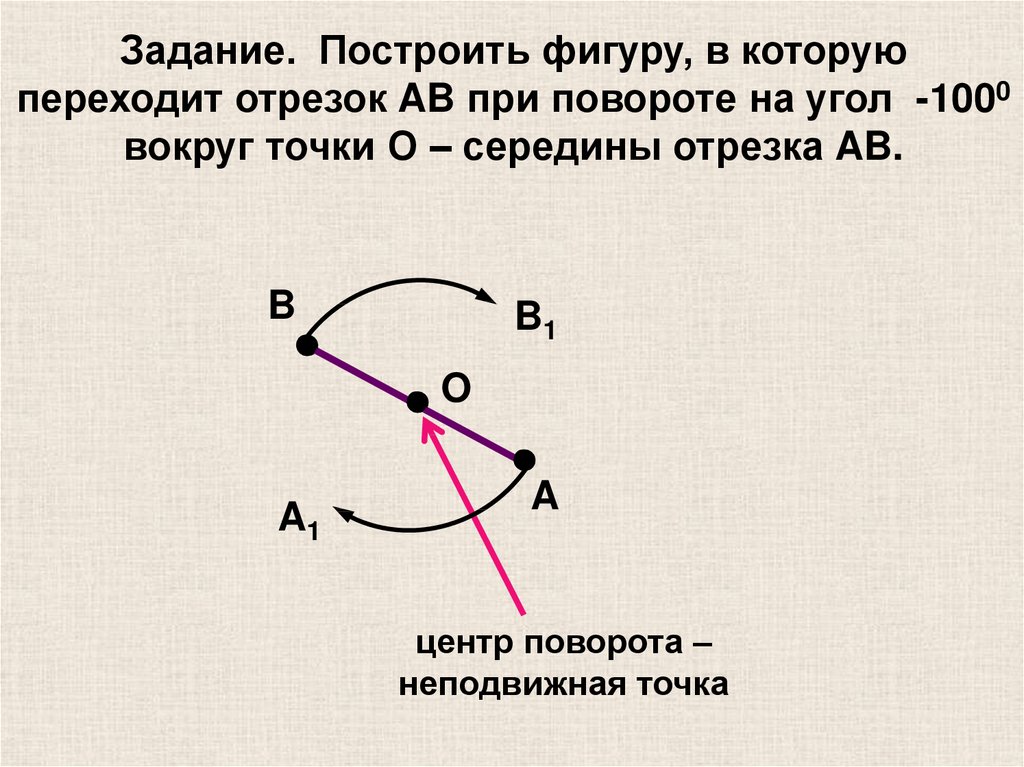
23.
Задание. Построить фигуру, в которуюпереходит отрезок AB при повороте на угол -1000
вокруг точки О – середины отрезка AB.
B
B1
O
A1
A
центр поворота –
неподвижная точка
24.
Центр поворота фигуры может быть вовнутренней области фигуры.
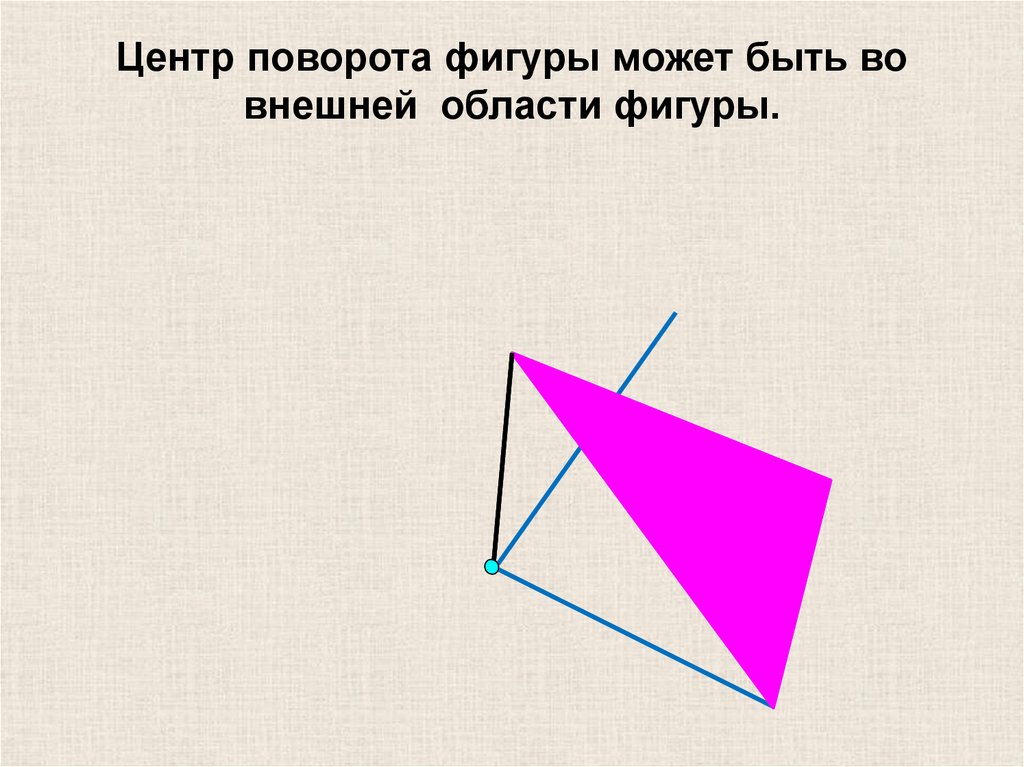
25.
Центр поворота фигуры может быть вовнешней области фигуры.
26.
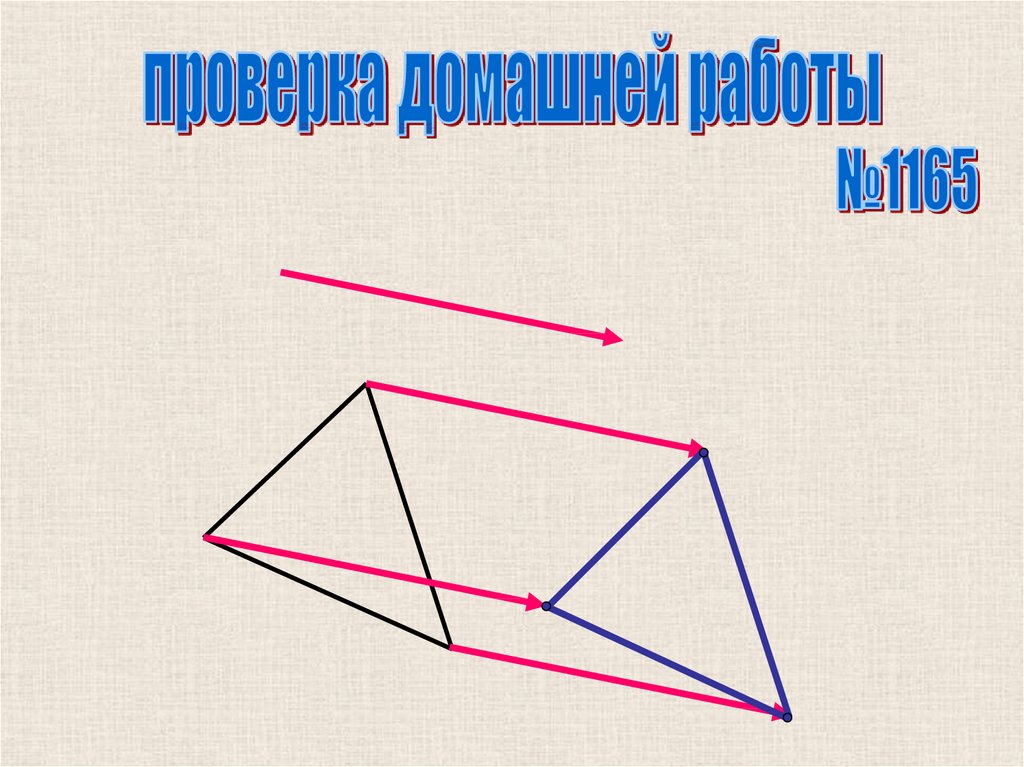
1. Определите по рисунку вид движения.а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение
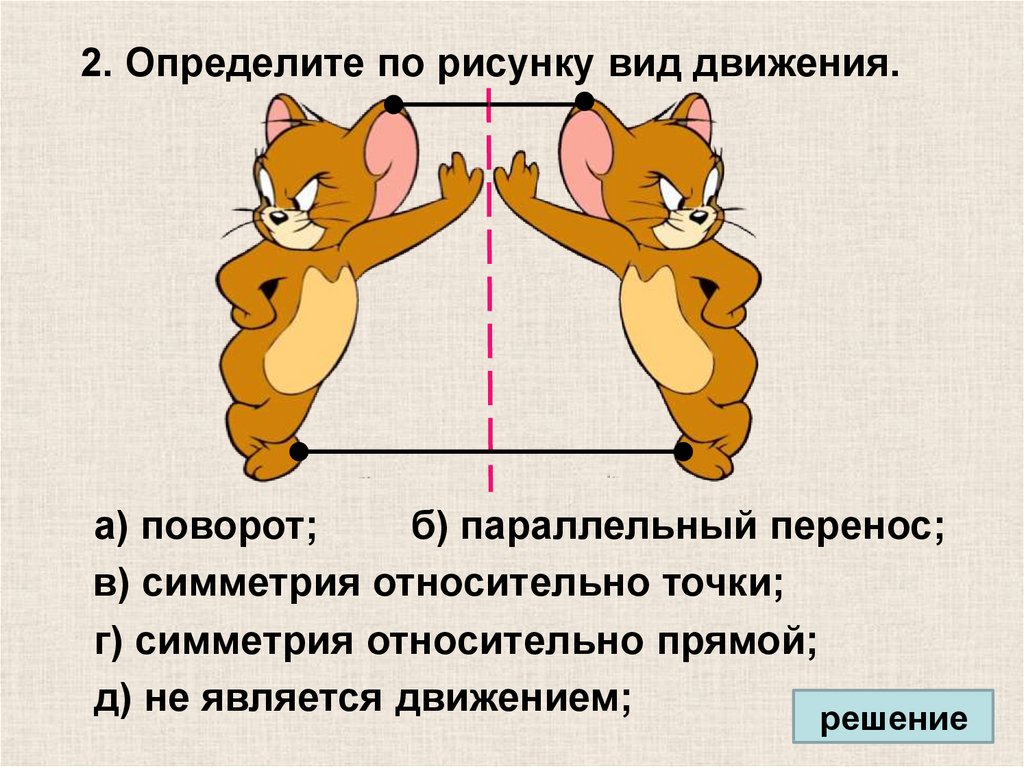
27.
2. Определите по рисунку вид движения.а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение
28.
3. Определите по рисунку вид движения.а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение
29.
4. Определите по рисунку вид движения.б) параллельный перенос;
а) поворот;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение
30.
5. Определите по рисунку вид движения.а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение















 mathematics
mathematics








